蒙特卡罗方法及其方差缩减技术比较分析

王立雪， 孙聚波， 徐平峰

（长春工业大学 基础科学学院，吉林 长春 130012）

0 引 言

蒙特卡罗方法起源于法国数学家布丰用投针实验的方法求圆周率π。20世纪40年代冯·诺依曼与S.M.乌拉姆做出了奠基性的工作，他们建立了概率密度函数、逆累积分布函数的数学基础。时至今天，众多学者对蒙特卡罗方法已作出了许多改进。这些方法都有其优缺点和适用范围，例如：对偶抽样在对偶变量和原始变量强负相关时表现很好；控制变量法的改进程度依赖于控制变量与待估变量的相关性；重要性抽样除了可以改进估计之外，另一个特点是当遇到不易抽样的分布时，可重新选择常见的、容易抽样的分布，但是如果选择的重要性函数不适当时，不仅不会减小方差，反而会大大增大方差。

蒙特卡罗方法的计算相对简单，即使所要解决的问题复杂度很高，也不会影响它的计算精度和收敛速度，而且所需存储的单元也很少，这些都是用该方法处理大型复杂问题时的优势。蒙特卡罗方法不仅较好地解决了多重积分计算［1］、微积分方程求解［2］、统计特征值计算［3］和非线性方程求解［4］等数值计算问题，而且广泛应用于金融工程学［5］、计 量 经 济 学［6－7］、生 物 医 学［8］、统 计 物 理学［9］等领域。

1 蒙特卡罗方法的基本原理及其计算精度

在数理统计中，很多感兴趣的量可以表示为某随机变量h（X）的期望，X的密度为f（x），则

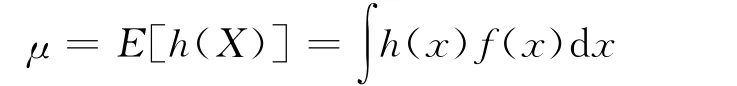
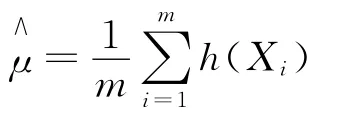
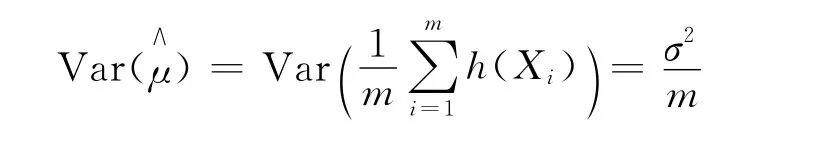
由中心极限定理知，当m足够大时

蒙特卡罗方法的估计μ∧与期望μ的误差为：

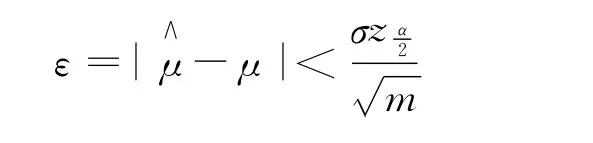
2 方差缩减技术

目前，常见的方差缩减技术有分层抽样法［10］、重 要 性 抽 样 法［11］、条 件 期 望 法［12－13］、对 偶变量法［10，14］、控 制 变 量 法［15］等，以 及 混 合 运 用 他们的技术。综合考虑技术的适用性和流行性，文中先简要介绍原始权重的重要性抽样法、标准化权重的重要性抽样法、对偶变量法、控制变量法，而后进行模拟研究。

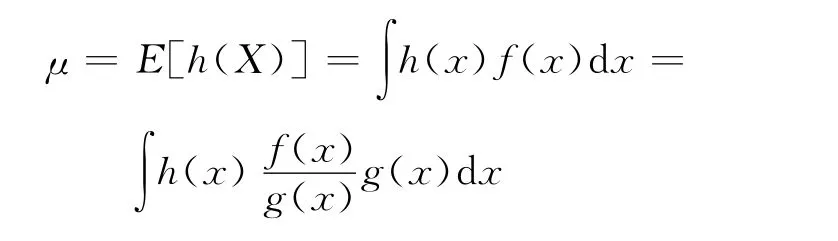
从g（x）中抽取i.i.d样本X1，X2，…，Xm，则μ的估计为：

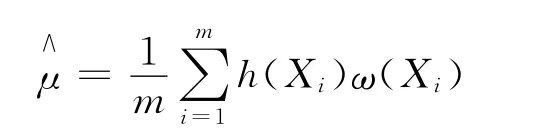
2.1 重要性抽样法

重要性抽样法通过改变现有样本空间的概率分布，提高“重要”区域的抽样权重，使对最后结果贡献大的样本出现的概率变大，以便减少方差，提高估计精度。

原始权重的重要性抽样原理：选取与f（x）有相同支撑集的另一个密度函数g（x），这里称其为重要性函数或包络函数。则期望可表示为：

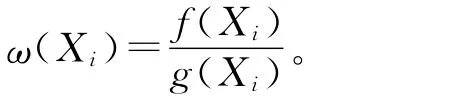
标准权重的重要性抽样原理：在标准权重的重要性抽样中，期望可表示为：

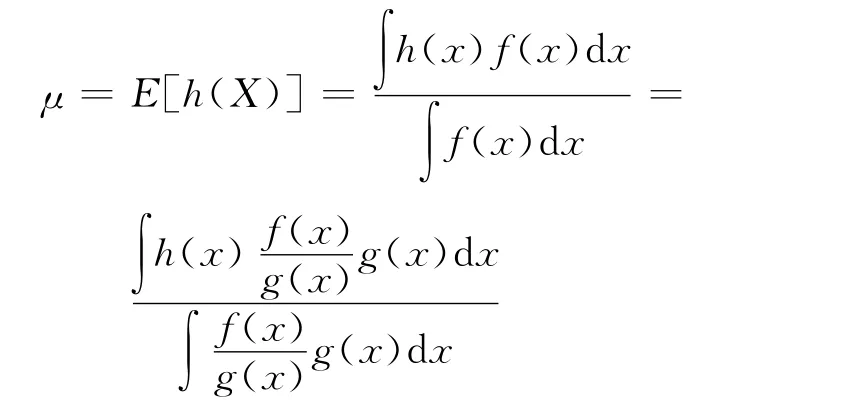
从g（x）中抽取i.i.d样本X1，X2，…，Xm，则μ的估计为：

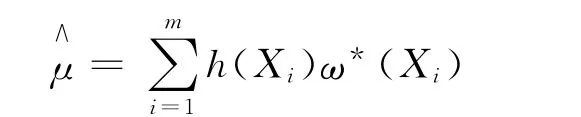
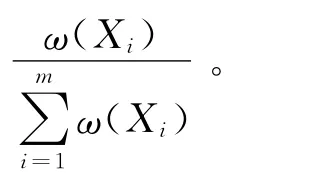
原始权重的重要性抽样步骤如下：

1）选取重要性函数g（x），从g（x）中抽取i.i.d样本X1，X2，…，Xm；

标准化权重的重要性抽样步骤如下：

1）选取重要性函数g（x），从g（x）中抽取i.i.d样本X1，X2，…，Xm；

2.2 对偶变量法

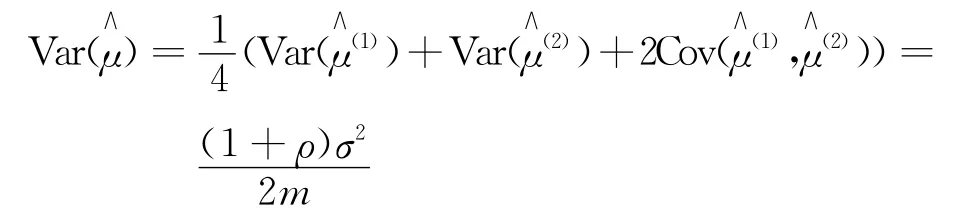
式中：ρ——两个估计的相关系数。

对偶变量法步骤如下：

1）从U（0，1）中产生m个随机数U1，U2，…，Um；

2）令

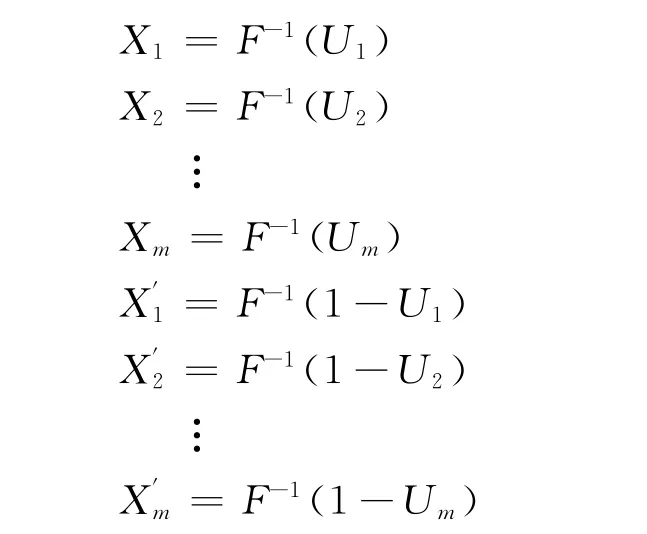
其中，F（X）为随机变量X的累积函数；

3）两个估计分别为：

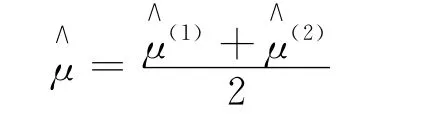
2.3 控制变量法

取与h（X）相关的随机变量t（X），它的期望已知为θ。θ和μ的简单蒙特卡罗估计为对常数c为μ的无偏估计，称其为控制变量估计，称t（X）为h（X）的控制变量。的方差为：

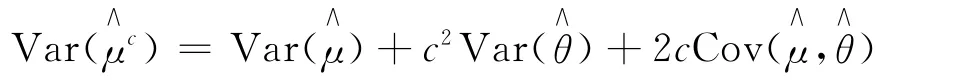
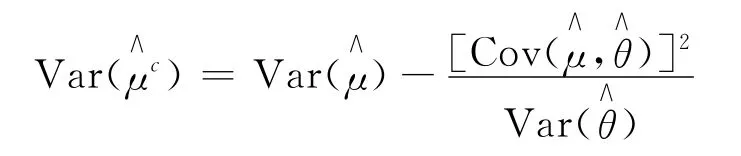
此时

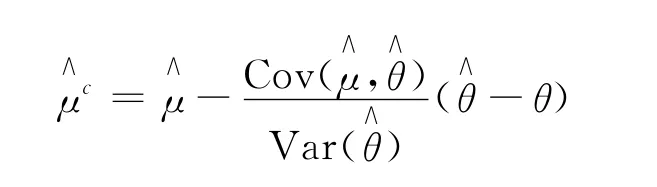
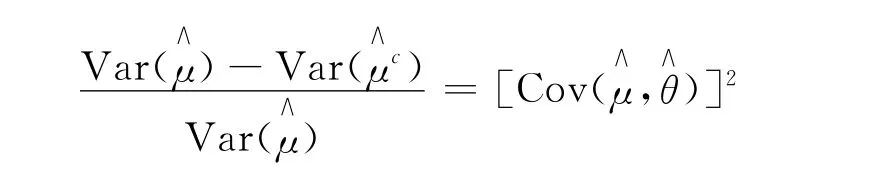
可以看出，控制变量t（X）与h（X）相关性越强，方差缩减率越大。

控制变量法步骤如下：

1）从f（x）中抽取i.i.d样本X1，X2，…，Xm；

2）选取控制变量t（X），其期望已知为θ，计算：

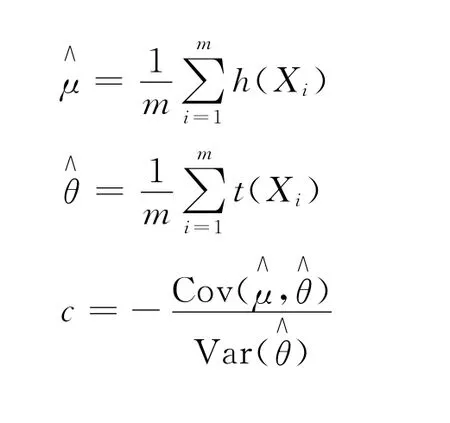
3 模拟研究

下面分别从数值分析和统计推断方面设计问题，通过模拟比较这几种方法的表现。问题1：求积分的估计值。被积函数在［0，1］上单调。我们选取的重要性函数，控制变量t（X）＝e－x都与h（X）比较接近。

问题1的模拟结果见表1。

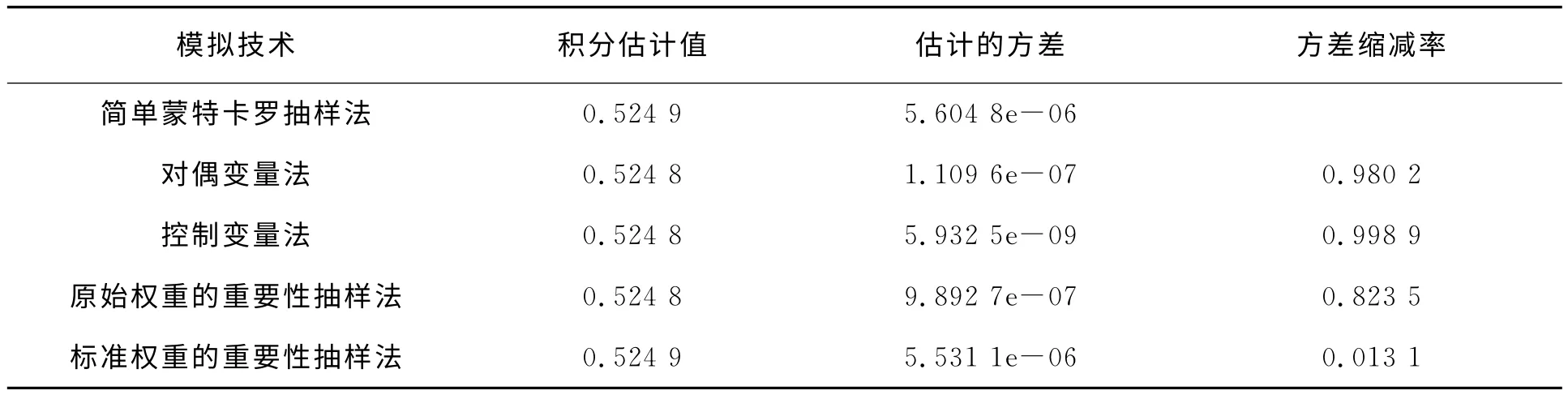
表1 问题1的模拟结果

从表1可以看出，几种方差缩减技术得到的积分估计值比较相近，没有明显差异。其中，由各技术的方差缩减率可知，原始权重的重要性抽样、控制变量法和对偶变量法的表现都很好，这依赖于模拟中取的重要性函数、对偶变量以及控制变量与原始变量的相关性都很强。

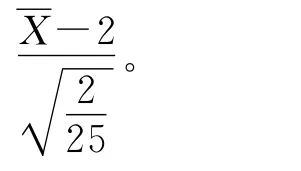
1）使用5种蒙特卡罗方法：简单蒙特卡罗抽样、对偶变量法、原始权重和标准化权重的重要性抽样，以及带控制变量的重要性抽样［16］，估计该检验的I型错误率。讨论每种方差缩减技术的表现。

2）对λ∈［2.2，4］，用同样的5种技术画出该检验的功效曲线。给出每种情况下的逐点置信区间。

在各种重要性抽样中，皆取λ＝2.465 3的Possion分布为重要性函数；在用控制变量改进的重要性抽样中，控制变量取为权重函数的样本均值

问题2中1）的模拟结果见表2。

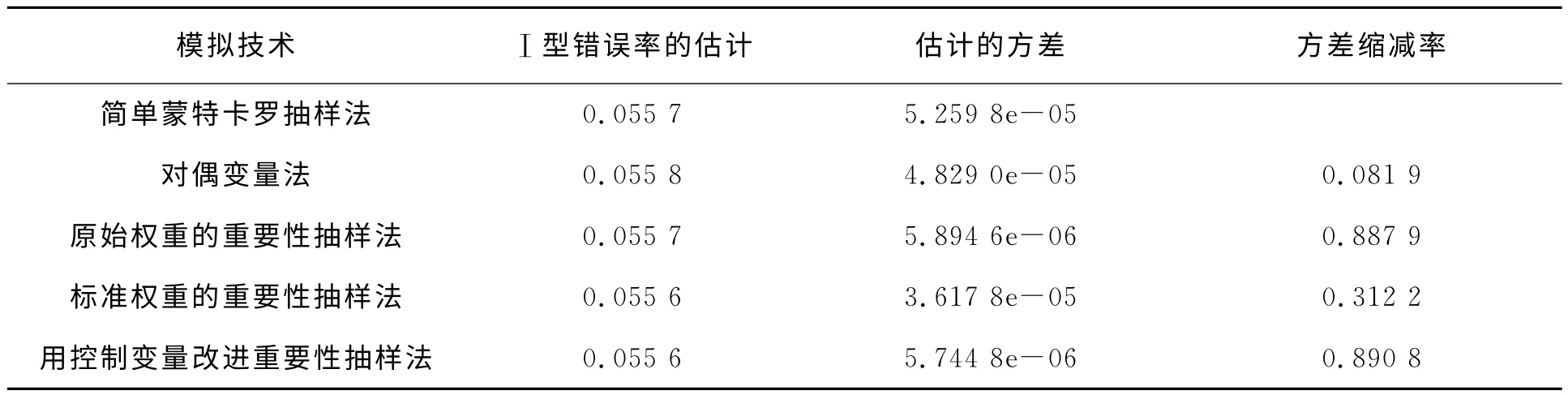
表2 问题2中1）的模拟结果

从表2可以看出，几种方差缩减技术得到的 Ⅰ型错误率的估计值都在0.055～0.056之间，没有明显的差异。其中，对偶变量法中的方差缩减率仅为0.081 9，对计算精度改进程度不大。同时也看到重要性抽样的方差缩减率为0.887 9，对计算精度的改进很大；相对地，标准化权重的重要性抽样的方差缩减率仅为0.312 2，结合表1可知，标准化权重未必能改进重要性抽样。最后，采用控制变量改进的重要性抽样法的方差缩减率为0.890 8，改进精度最好。

下面给出问题2中2）用5种技术画出的功效曲线和逐点置信区间，直观地显示了这几种方法的表现，分别如图1～图5所示。

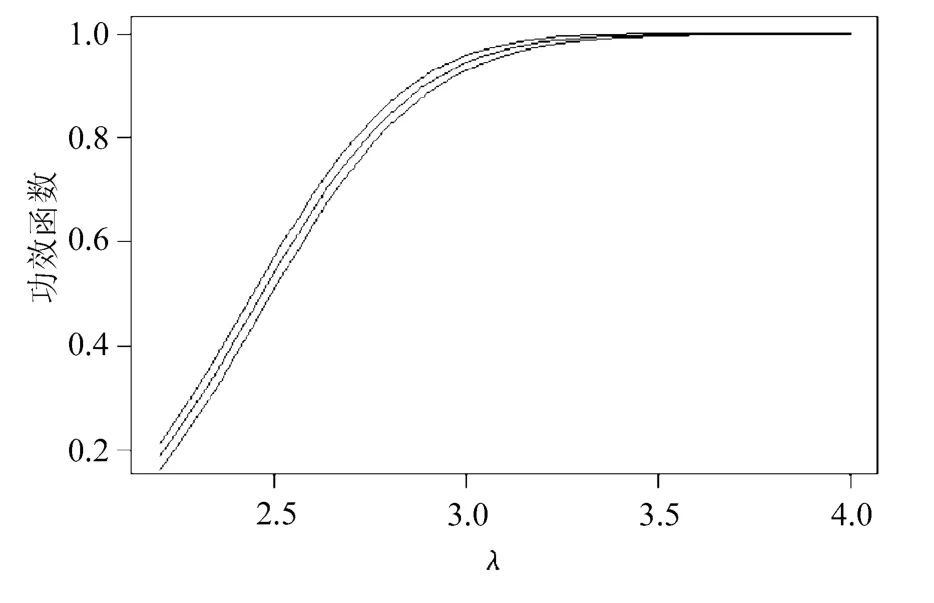
图1 简单蒙特卡罗抽样的功效及置信区间

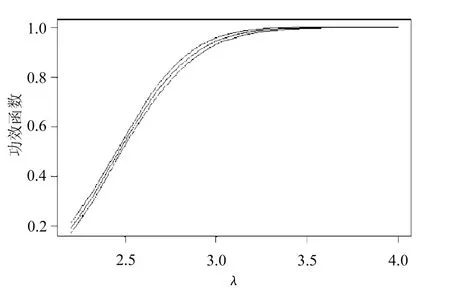
图2 对偶变量法的功效及置信区间

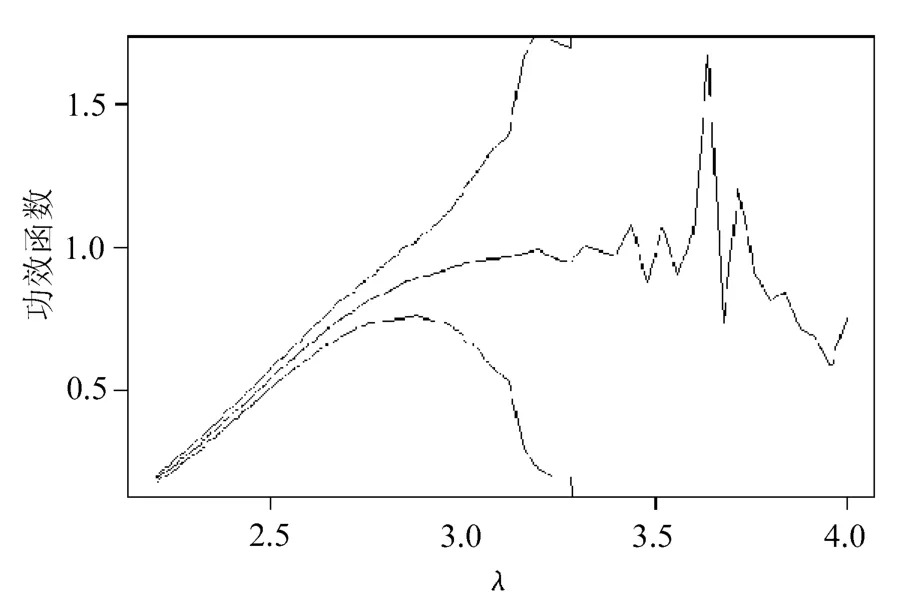
图3 原始权重的重要抽样的功效及置信区间

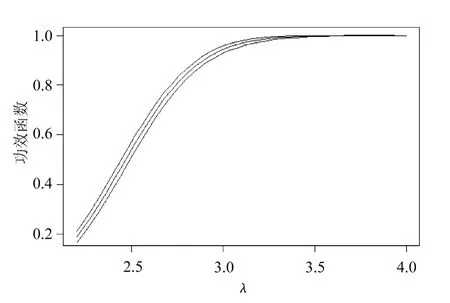
图4 标准权重的重要抽样的功效及置信区间

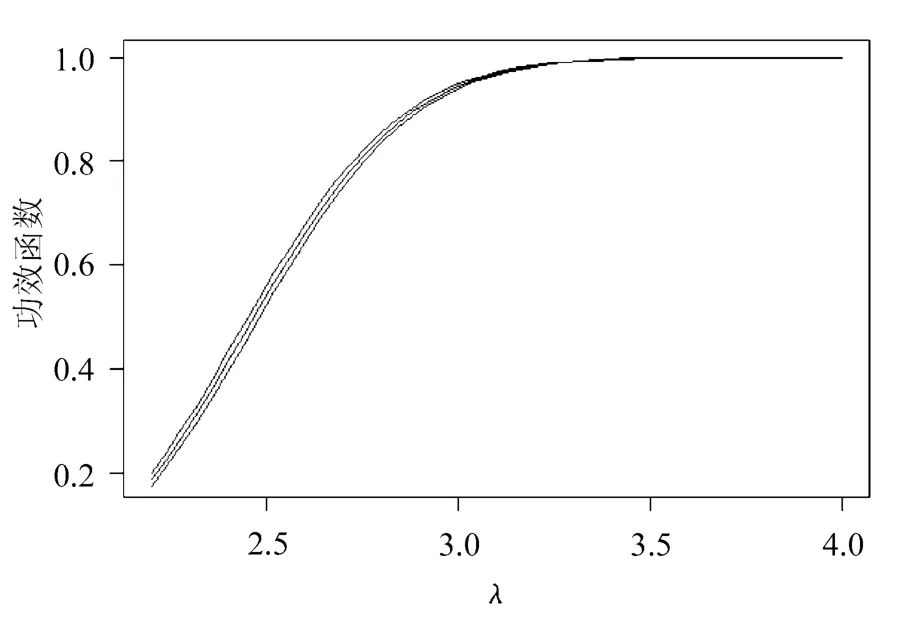
图5 带控制变量的重要性抽样的功效及置信区间

从图2、图4与图1的比较中可以看出，对偶变量法、标准权重的重要性抽样二者无论是在待估功效很小还是很大时都有改进，表现相对稳定。再观察图3可知，原始权重的重要性抽样在估计功效很小时方差非常小，估计精度很好，但随着估计功效的增大，估计越来越不稳定，以至让人无法接受的程度，这恰恰反映了原始权重的重要性抽样更适合估计小概率问题。通过图1～图5的比较可知，带控制变量的重要性抽样表现是5种技术中最好的，它对重要性抽样改进很大。

4 结 语

综合理论知识和模拟结果，蒙特卡罗方法及其改进方法利用产生的大量随机样本来估计问题，简单易行。文中列举的方差缩减技术都有其特点和适用范围，若将各种技术结合使用，可以有效地减小方差，提高计算精度。

［1］ 同济大学计算数学教研室.现代数值计算［M］.北京：人民邮电出版社，2009.

［2］ 洪志敏.基于Monte－Carlo技术的积分（微分）方程数值求解方法研究［D］.呼和浩特：内蒙古工业大学，2013.

［3］ 王克冲.用蒙特卡洛法求多维随机变量函数的统计特征值［J］.南京理工大学学报：自然科学版，1986（1）：77－81.

［4］ 王克，薛小超，朱朋海.非线性方程的多核并行蒙特卡洛求解方法［J］.现代计算机：中旬刊，2014（7）：38－44.

［5］ P Glasserman.金融工程中的蒙特卡罗方法［M］.范韶华，孙武军，译.北京：高等教育出版社，2013.

［6］ D N Gujarati，D C Porter.计量经济学基础［M］.费剑平，译.5版.北京：中国人民大学出版社，2011.

［7］ 董小刚，王淑影，王纯杰.基于动态因子的经济水平差异分析［J］.长春工业大学学报，2015，36（2）：125－129.

［8］ 任晓楠，魏守水，杨宪章，等.光能量在生物组织中传输的蒙特卡罗研究［J］.生物医学工程学杂志，2010（3）：652－657.

［9］ K Binder，D W Heermann.Monte carlo simulation in statistical physics［M］.5th edition.北京：世界图书出版公司，2014.

［10］ S M Ross.Simulation［M］.2nd edition.San Diego，CA：Academic Press，1997.

［11］ G H Givens，J A Hoeting.Computational statistics［M］.Wiley：［s.n.］，2005.

［12］ G Casella，C Robert.Rao－Blackwellization of sampling schemes［J］.Biometrika，1996，83：81－94.

［13］ A Gelfand，A F M Smith.Sampling based approaches to calculating marginal densities［J］.Journal of the American Statistical Association，1990，85：398－409.

［14］ J M Hammersley，K W Morton.A new monte carlo technique：antithetic variates［J］.Mathematical Proceedings of the Cambridge Philosophical Society，1956，52：449－475.

［15］ J S Liu.Monte carlo strategies in scientific computing［M］.New York：Springer－Verlag，2001.

［16］ T Hsterberg.Weighted average importance sampling and defensive mixture distributions［J］.Technometrics，1995，37：185－194.