一条焦点弦 年年高考题——由一道课本例题到高考题的再探讨

曹凤山 (余杭高级中学 浙江杭州 311100)



一条焦点弦 年年高考题
——由一道课本例题到高考题的再探讨

曹凤山 (余杭高级中学 浙江杭州 311100)

笔者曾在拙文[1，2]中对课本一道例题(人教A版选修2-1第69页例4)如何演变到高考题，以及该例题本身作了一些引申、推广.从近2年的高考题可以看出，从该例题“生发”出的高考题依然源源不断，且命题手段不断翻新，对该例题的进一步挖掘也仍然很有意义.

例1 斜率为1的直线l经过抛物线y2=4x的焦点F，且与抛物线相交于点A,B，求线段AB的长.

图1

由图1可以看出，该例题涉及的直线上有不少重要的点，可谓一条名副其实的“珍珠链”，如焦点F，直线与抛物线2个交点A,B，与y轴的交点C，与准线的交点G以及弦AB的中点H等.从命题角度看，其中任意取2个点就有长度问题，3(或4)个点就有线段比值问题，结合原点等直线外的点就有面积(比)问题等.这些问题都涉及核心知识，命题手法多种多样，解题通性通法突出.由于圆锥曲线的统一性，对于椭圆、双曲线的相应问题也有很大的挖掘空间.

1 长度问题

首先给出大家熟知的结论：

结论1 如图1，过抛物线y2=2px(其中p>0)的焦点F、倾斜角为θ的直线l交抛物线于点A,B，则

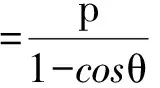
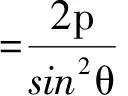
从结论1可以看出，抛物线的通径为2p，是最短的焦点弦.

变式 当直线AB的斜率存在时，焦点弦

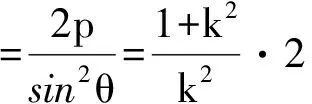
例1中，k=1(即θ=45°)，p=2,故|AB|=8.

高考类题

1.设F为抛物线C：y2=3x的焦点，过点F且倾斜角为30°的直线交C于点A，B，则|AB|=

( )

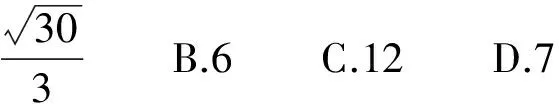
(2014年全国数学高考新课标卷文科试题)

2 线段比问题

2.1 焦点分焦点弦的情形

图2

如图2，设BF=a,由抛物线的定义知BB1=a，AA1=λa.在△ABC中，AC=|λ-1|a,AB=(λ+1)a,从而

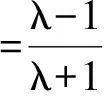
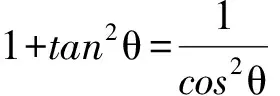
结合结论1，知：

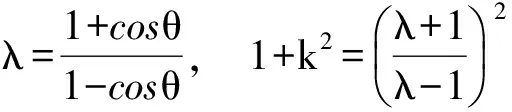
高考类题

2.设抛物线C:y2=4x的焦点为F,直线l过点F且与C交于点A,B.若|AF|=3|BF|,则l的方程为

( )

A．y=x-1或y=-x+1

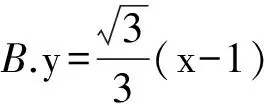
(2013年全国数学高考课标卷文科试题)

(这里p=2，λ=3,由结论2知，k2=3，故选C.)

(2012年重庆市数学高考理科试题)

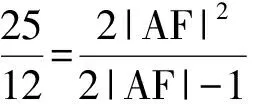
4.已知F是抛物线C:y2=4x的焦点，过点F且斜率为1的直线交C于点A,B．设|FA|>|FB|，则|FA|∶|FB|=______．

(2008年全国数学高考理科试题)

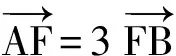
(2010年重庆市数学高考理科试题)

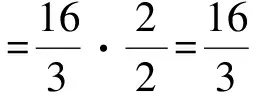
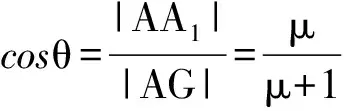
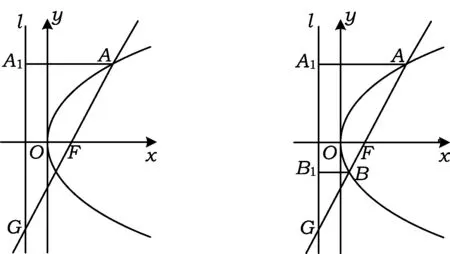
图3 图4

2.3 抛物线上点分焦点与准线交点的情形

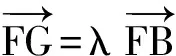
故

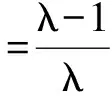
高考类题

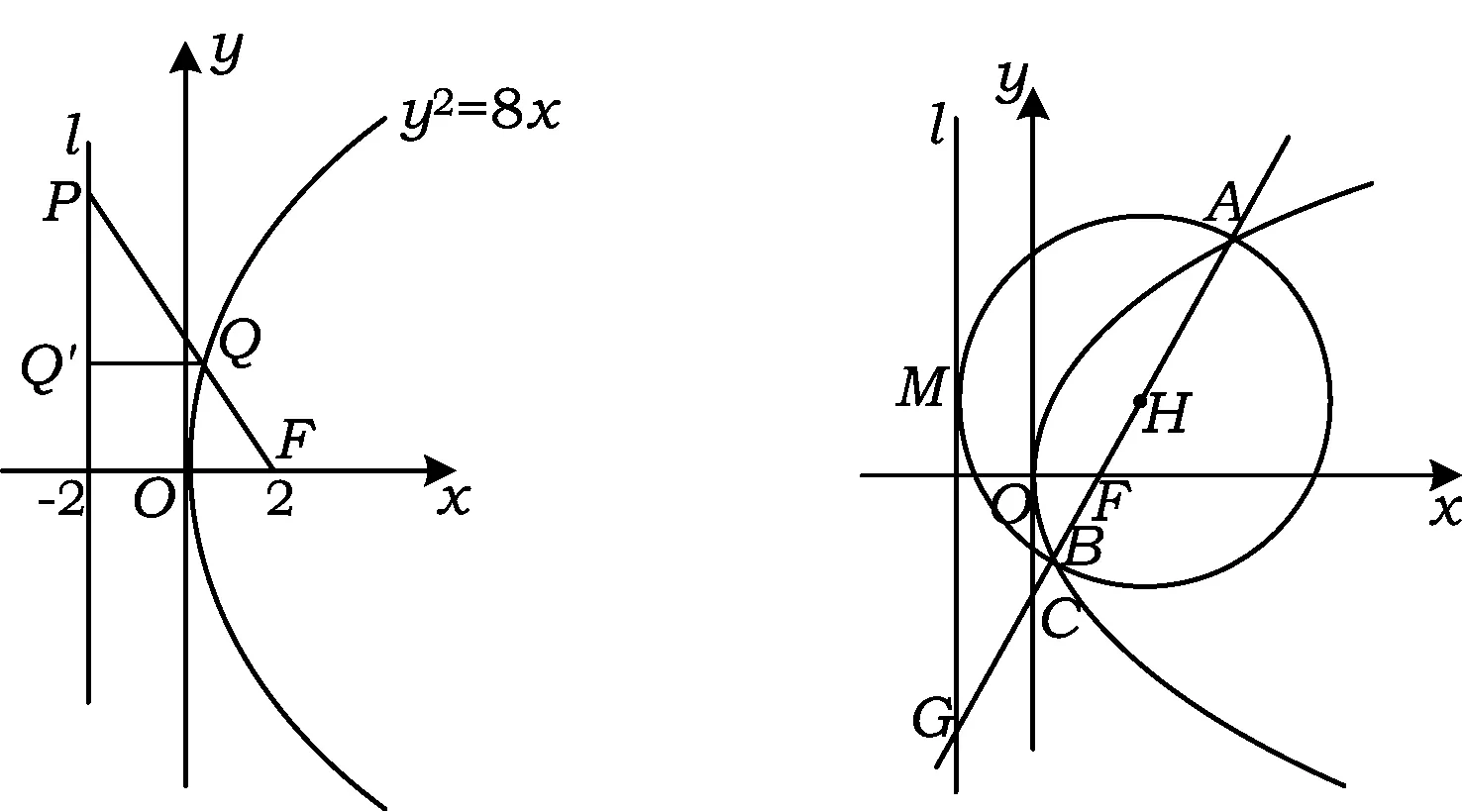
图5 图6

( )

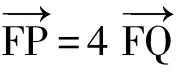
(2014年全国数学高考新课标卷试题)

3 以线段为直径的圆问题

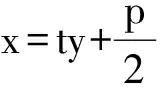
y2-2pty-p2=0,

从而

y1+y2=2pt,y1y2=-p2.

于是

图7

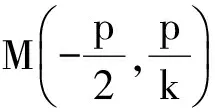
高考类题

( )

(2014年全国数学高考大纲卷理科试题)

8．设抛物线C:y2=2px(其中p>0)的焦点为F,点M在C上,|MF|=5,若以MF为直径的圆过点(0,2),则C的方程为

( )

A．y2=4x或y2=8xB．y2=2x或y2=8xC．y2=4x或y2=16xD．y2=2x或y2=16x

(2013年全国数学高考新课标卷理科试题)

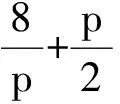
4 面积问题

根据结论1和结论2，在抛物线中的面积问题，易得以下结论：

结论7 过抛物线y2=2px(其中p>0)的焦点F、倾斜角为θ(斜率为k)的直线l交抛物线于点A,B，则

结论8 过抛物线y2=2px(其中p>0)的焦点F、倾斜角为θ(斜率为k)的直线l交抛物线于点A,B，则

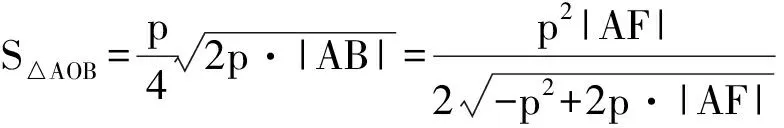
高考类题

9.设F为抛物线C：y2=3x的焦点，过点F且倾斜角为30°的直线交C于点A，B，点O为坐标原点，则△OAB的面积为

( )

(2014年全国数学高考新课标卷试题)

10.过抛物线y2=4x的焦点F的直线交抛物线于点A,B,点O是原点.若|AF|=3,则△AOB的面积为

( )

(2012年安徽省数学高考理科试题)

( )

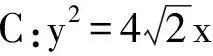
(2013年全国数学高考课标卷文科试题)

12.在直角坐标系xOy中,直线l过抛物线y2=4x的焦点F,且与该抛物线相交于点A,B,其中点A在x轴上方.若直线l的倾斜角为60°,则△OAF的面积为______.

(2012年北京市数学高考理科试题)

[1] 曹凤山.从课本例(习)题到高考题的若干命题途径[J].中学教研(数学),2012(1):26-28.

[2] 曹凤山.你能看出结果吗？——以一道例题的探究为例[J].中学数学教学参考:上半月,2011(9):37-39.