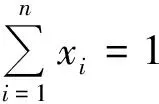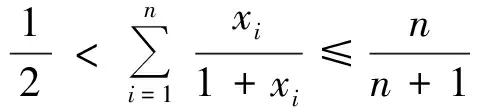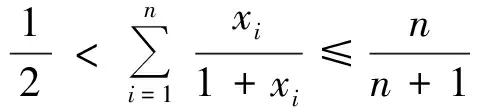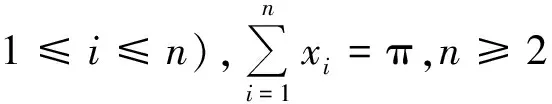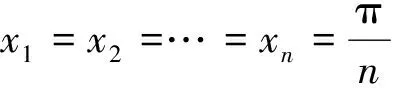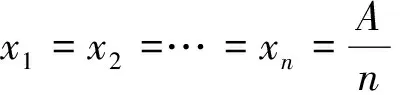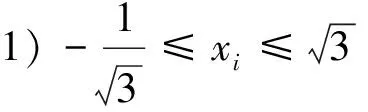巧用“凹凸” 妙得最值——一个凸函数命题的探究和应用

吕孙忠 (北京师范大学研究生院 北京 100875) ●沈 亚 (杭州市第四中学 浙江杭州 310018)



巧用“凹凸” 妙得最值
——一个凸函数命题的探究和应用

吕孙忠 (北京师范大学研究生院 北京 100875) ●沈 亚 (杭州市第四中学 浙江杭州 310018)

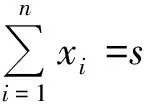
证明 求最大值时，可用数学归纳法证明.当n=2时，若s≤a+b，对于x1,x2∈[a,s-a]，存在参数0≤t≤1，使得

x1=ta+(1-t)(s-a)，

x2=(1-t)a+t(s-a).

由Jensen不等式，可得

f(x1)≤tf(a)+(1-t)f(s-a),

和

f(x2)≤(1-t)f(a)+tf(s-a)，

从而

f(x1)+f(x2)≤f(a)+f(s-a).

若s≥a+b，可以用类似方法证明

f(x1)+f(x2)≤f(b)+f(s-b).

因此当n=2时，结论成立.若当n=k时，结论成立,则当n=k+1时，

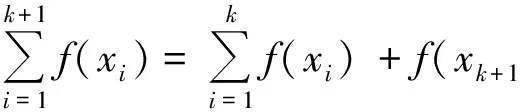
首先将xk+1视为常量，由于xk+1∈[a,b]，得

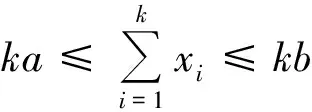
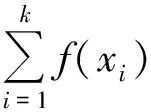
f(xk)+f(xk+1)+lf(a)+(k-1-l)f(b)，

其中xk=s-xk+1-la-(k-l-1)b.再将xk+1视为自变量，利用当n=2时的结论，当f(xk)+f(xk+1)取到最大值时，xk或xk+1中至少有1个为a或b，综上可得x1,x2,…,xk+1中至少有k个元素等于a或b.即当n=k+1时结论成立，因此对一切正整数n都成立.

求最小值时，根据凸函数的性质，利用Jensen不等式即可，这里就不再赘述了.

注 命题1中最大值的结论是文献[1]给出的，但文献[1]仅给出了变量数为2时的证明.笔者结合文献[1]中的结论和Jensen不等式，总结形成了命题1，并给出了变量数为n时的证明.

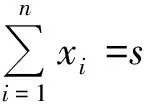
注 命题2是笔者在命题1的基础上改编的.由条件可知f(x)是[a,b]上的凹函数，从而f′(x)≤0，于是-f′(x)≥0，可知-f(x)是定义在实数[a,b]域上的凸函数，那么命题2的证明就转化成了命题1的证明.

下面的内容主要利用命题1和命题2来解决和推广一些实际例子，以供大家参考.

( )

A.1个 B.2个 C.3个 D.4个

(2012年“华约”自主招生试题)

分析 此题以填空题的形式出现，相信很多考生刚拿到题目时，无法从最大值的条件逆推出等于-6的个数.但如果站在命题1的高度上看待此题，那么答案便手到擒来.

-6≤50-[-6x+10×(9-x)]≤10，

解得

34≤16x≤50，

又因为x为整数，所以x=3.故选C.

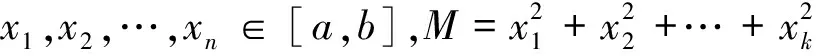
分析 此题的关键是确定x1,x2,…,xn中a和b的个数，可设a的个数为x，根据命题1，限制最后一个变量的取值范围：a≤s-ax-(n-1-x)b≤b，化简得

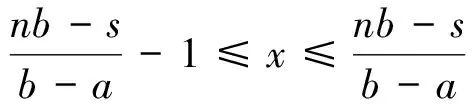
即

代入即可求得最大值和最小值.

注 由于区间[a,b]的任意性，推论1中的f(x)必须是整个实数域上的凸函数，而形如x2k,x2k+c,(x+c)2k(其中k∈Z+)这一类函数都符合该要求，如果将推论1扩展到上类函数上去，也会得到类似的结论.另外，计算a和b个数的公式不管是凹函数还是凸函数都是通用的，可作为一个结论单独使用.

注 用了“至少”是因为最后一个变量也有可能是a或b，证明过程见推论1.

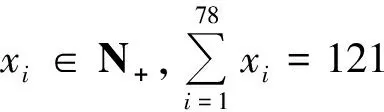
(《数学通讯》2014年第4期问题172)

分析 此题的特点是没有直接给出自变量的取值范围，却隐晦地给出了求解自变量取值范围的条件.因此,在解题前先要确定xi的取值范围，再利用推论1便可解决问题.总之，要善于挖掘题干中的隐藏条件，找到切入点，那么解题思路便会浮现在眼前.

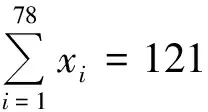
xk≤121-77=44(其中i=1,2,…,121)，

即

1≤xi≤44(其中i=1,2,…,78).

根据推论1，当P取到最大值时，1的个数为77，44的个数为1，于是P的最大值为2 013.

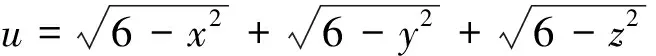
(2013年全国高中数学联赛B卷加试题)

则

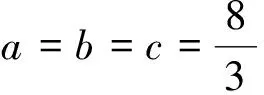
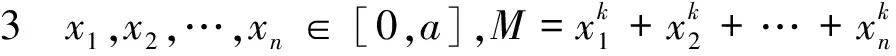
1)若k>1或k<0，则

Mmax=[m]ak+(ma-[m]a)k，

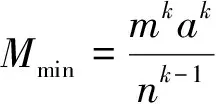
2)若0

Mmin=[M]ak+(ma-[m]a)k.

分析 令f(x)=xk,当k>1或k<0时，

f″(x)=k(k-1)xk-2≥0，

可知f(x)为凸函数，根据命题1，x1,x2,…,xn中至少有n-1个0或a，不妨设a的个数为x，则0≤ma-ax

注 相比推论1，由于推论3中自变量的取值范围限制在[0,a]，故对形如xk(其中k≠1)的函数都存在一般结论，但需要注意的是，函数的凹凸性会随着数值k的改变而改变.

(《数学通讯》2014年第4期问题175)

分析 类似于例3，若直接求导过程太过复杂，则可以通过适当转化和变形来减少求导过程中产生的计算量.此外，还要注意的一个条件是：xi为正实数，取不到0.

分析 一般情况下，三角函数会在边界点或者各个变量取相等值时取到最值，但这种感性的判断缺乏科学的依据.而sinx在x∈[0,π]为凹函数是本题的切入点.

注 三角函数在某些区间上具有凹凸性，因此我们可以在特定的区间里，利用凹凸函数的性质来研究三角函数的最值.

练习

1.设实数x1,x2,…,x1 997满足如下2个条件：

(第12届CMO试题)

2.已知a,b为非负数，M=a4+b4，a+b=1，求M的最值.

(2006年清华大学自主招生试题)

[1] 范建熊，隋振林.不等式的秘密[M].哈尔滨：哈尔滨工业大学出版社，2014.