基于微专题教学的一些实践与思考——由一道模拟题说起

李宽珍 (溧水高级中学 江苏溧水 211200)



基于微专题教学的一些实践与思考
——由一道模拟题说起

李宽珍 (溧水高级中学 江苏溧水 211200)

1 问题的提出

微专题是指一个相关联的、可以单独研究的知识体系、某种数学思想方法、一个研究主题等，根据学生不同学习阶段具有一定弹性，又称小专题.微专题教学是指针对某一具体知识点，从该知识的基本概念、基本原理、基本规律入手，内化知识，构建结构进行知识迁移，整合并能运用基本概念和原理解决实际问题的一种“小切口”教学方法.其涵盖的内容适量，知识间联系紧密，可以在学习基础知识的同时，帮学生形成良好的认知结构，活化知识的运用，提升解决问题的能力.

高三复习期间笔者选取了2015年江苏省南通市一模第13题给学生练习，这是一道三角、向量综合题，结果学生的解答很不顺利，错误百出，令人诧异.因此，笔者对此题进行了反思和拓展，并以这道题为中心设计了一节向量中有关于模与夹角问题的微专题，收到了良好的教学效果.下面将此微专题的教学过程叙述如下，欢迎指正.

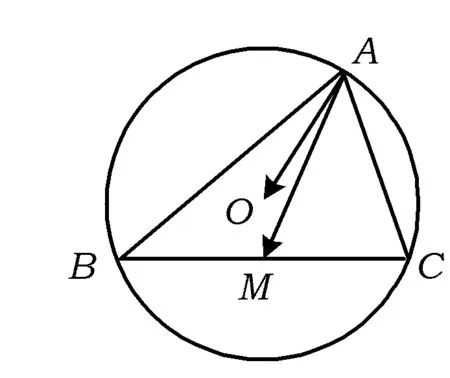
图1

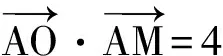
(2015年江苏省南通市一模第13题)

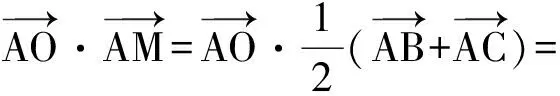
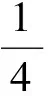
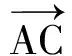
2 课堂实录

活动1 课本溯源

师：下面2道题来源于苏教版教材必修4第84页练习2，大家做做看：

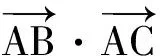
生1：可以利用向量转化：

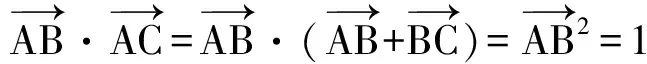
生2：也可以用向量的定义解决：

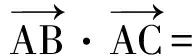
在直角三角形中，有

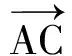
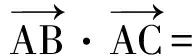
师：很好！这2位同学分别运用了基向量的思想和向量数量积的定义来解决此题，看到了问题的本质.

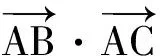
生3：联结BD，交AC于点O，则点O为AC的中点，且AC⊥BD，从而

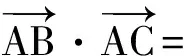
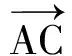
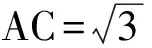
师：若能认识到问题的本质，此类题目就会简单易解，原题自然就不会有那么高的错误率了！

活动2 模式提炼

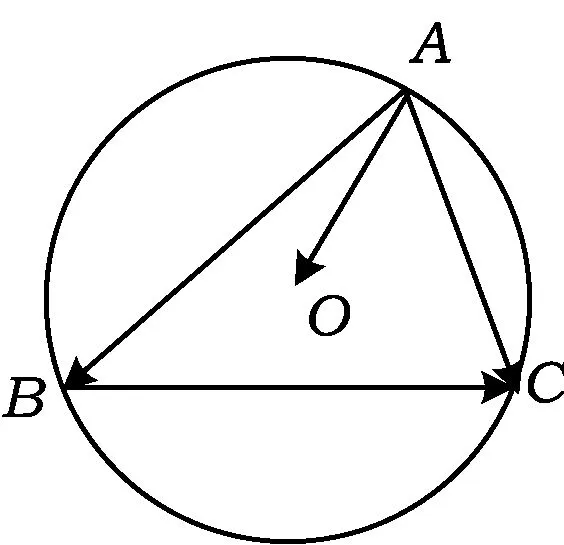
图2

师：以上几道题的核心其实是向量题中的一个基本模型，具体如下：

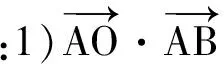
师：你能给出证明吗？

生4：1)证法1 如图3，取AB的中点为M，联结OM，则

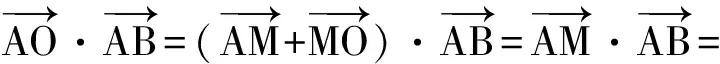
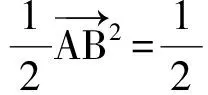
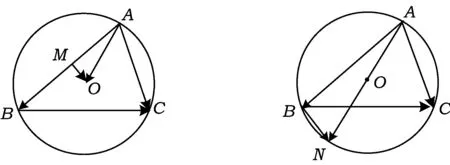
图3 图4

证法2 如图4，延长AO交圆O于点N，联结BN，则

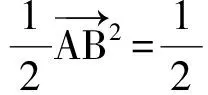
2)同第1)小题的证法.

3)用第1)小题的证法，或者由第1)，2)小题的结论可得

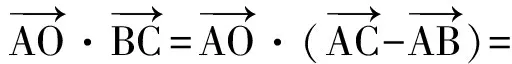
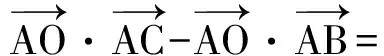
由此可以得到如下基本模式：在△ABC中，3条边长分别为a,b,c，点O是△ABC的外心，则

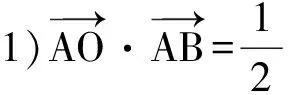
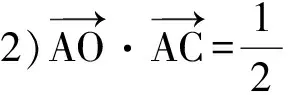
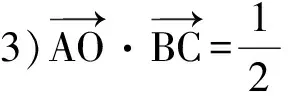
活动3 实战演练

师：我们刚刚提炼出这个基本模式，大家赶快试试，用它来解决下面的问题吧！

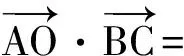
(2011年江苏省南京市外国语学校高三调研试题)

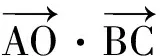
(2012年江苏省无锡市高三期末考试试题)

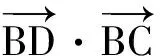
这些题目中都蕴含了一定的基本模型，是基本概念、基本方法的具体体现，掌握了基本模型，就为解题提供了方向，找到了问题转化的途径和突破口.基于模式辨别的一类微专题的设置更具有针对性，易将零散的知识串联，可以帮助学生对问题的核心有更深的认识，更能厘清向量与数量之间的转化关系，促进认知策略的获得与迁移，从而提高了学生的解题能力，加深了学生对数学概念、方法等的认知.

3 关于微专题教学的一些思考

本节微专题教学是针对学生在处理和三角形外心相关的数量积问题时遇到的障碍而设计的.在教学中，通过微专题的形式提炼一些基本模型，旨在揭示问题的本质，达到“会一题，通一类”的目的，有助于提高学生的解题能力，增强数学理解力.运用微专题教学，呈现出以下特点：

3.1 基于“以退为进,循序渐进”的原则

华罗庚说：要善于退，足够的退，退到最原始又不失一般性的地方，是学好数学的诀窍.因此，对于学生遇到的问题，教师要善于“退”，在设计问题呈现上，考虑分层次的“退”，退到最基本的概念上去获得能力，即以基本概念为抓手，逐步延伸拓展，循序渐进地“进”到原题的解答，问题的核心.例如，本微专题中，抓住学生的难点，找到学生的思维障碍，回到最基本的概念——数量积的概念及其几何意义.通过解决课本的基本题型，让学生熟练其来龙去脉，再加以变式、延伸、拓展，以各种不同的题境呈现，将一个个知识点串“珠”成“链”，利于学生对这个问题的深层次把握，益于整体思维的构建.

3.2 基于学生的问题为出发点，突出思维诊断

微专题教学通常选择热点、难点、疑点等“点问题”进行深层次研究，根据知识间的联系和相通之处，让学生理解一点，学会以点带面，举一反三，融会贯通，起到点石成金之效，达到提升学生观察能力、分析能力、创新能力.因此，本微专题基于学生的思维障碍处设计，选择学习中的难点，逐步将难点剖析.

在复习向量期间，笔者给学生做了2013年苏北三市高三第2次调研考试第14题，错误率也很高.

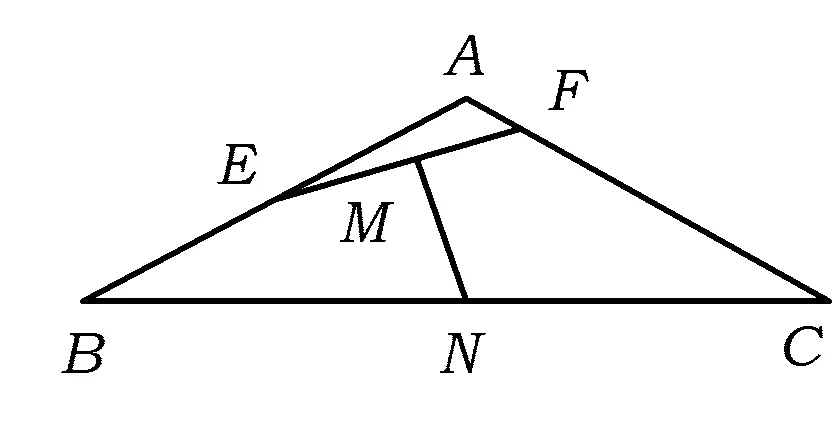
图5

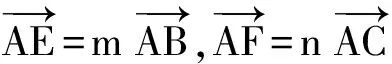
对例4的分析，若仅仅停在表面，学生收获很小，下次遇到类型相同的题目，变换一下条件，学生还是不能顺利解答.不妨以此题的核心部分设置微专题，抓住问题的本质，逐步将问题展开.例4的核心其实是苏教版教材第72页中的一道习题：

图6 图7

以例5为出发点，引导学生深刻理解解决该问题的思想方法，再对此题进行延伸，变换题目出现的条件：

变式 如图7，在正△ABC中，点D在边AB上，AD=1，点E在边BC上，CE=2，点M，N分别为线段DE，AC的中点，则MN=______．

(2012年江苏省苏州市考前综合题)

3.3 注重知识的整合，以小见大

微专题教学不仅要“微”，而且更要“专”，因此更注重知识间的整合和联系，强调“大处着眼，小处着手”.有针对性、选择性地选择一定的问题，让学生带着问题学习，在设问和释问的过程中优化学习方法，优化思维品质，在解决问题的进程中获得能力.学生参与了知识的建构，了解了知识的来龙去脉，就可以从中得到感悟和体验，从而达到小中见大、见微知著的效果.

例6 已知4x2+y2+xy=1，求2x+y的最大值.

这是一道常见题.在复习基本不等式时，经常会用来考查学生是否掌握了基本不等式成立需要满足的3个条件.为此除了纠正学生易犯的错误外，大多数教师都是会采取配方法，再运用不等式的方法解决：

原等式等价于(2x+y)2=3xy+1，再利用基本不等式得

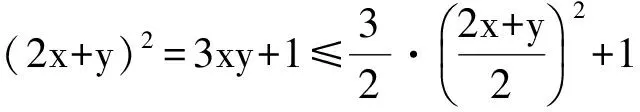
解得

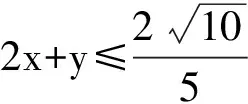
笔者在讲授例6时，设置了关于这类问题的一个微专题，力求让学生发现这类题的本质：

例7 已知x2+y2=1，求2x+y的取值范围.

这是一道常规题，学生大致可以想到3种方法解决：

方法1 令2x+y=t，视为直线与圆有交点，即相交或相切，转化为线性规划问题求解.

方法2 三角换元.令x=cosθ,y=sinθ，其中θ∈[0,2π),代入所求式子再用辅助角公式易解.

方法3 令2x+y=t，与圆方程联立，转化为代数问题：方程有根，根据判别式Δ≥0可求得范围.

具体解法略.接着，对例7进行变式、拓展：

变式1 已知4x2+y2=1，求2x+y的取值范围.

对于变式1，以上3种方法均可求解，也可以利用基本不等式：

方法4 先化简为4x2+y2=(2x+y)2-4xy，再利用基本不等式.

变式2 已知4x2+y2+xy=1，求2x+y的取值范围.

对于变式2，方法3和方法4可以，其余不行.

变式3 已知3x2+y2+xy=1，求2x+y的取值范围.

对于变式3，只有方法3可行.

由此可以看出，此类问题的本质是直线与曲线相交求范围问题，即点在曲线和直线上，联立方程组，转化为方程有解问题.只有让学生认清了问题的本质，无论题目千变万化，都能迅速获得关联点，实现知识、方法的迁移.

微处即为精华，微处即为根本.微专题教学主张知识方法的串联、整合，由易到难，层次分明，循序渐进，力求贴近学生的知识经验和能力基础，贴近学生的情感态度与思维水平，使得学生的技能水平自然而然地得到提高，由“见山是山”达到“见山不是山”、“见山还是山”的境界，真正实现微专题复习的优效教学.

[1] 刘永东．例谈数学小专题复习中的策略与应用[J]．教育导刊，2013(1)：87-89.

[2] 刘超.谈“小专题复习法”在高三生物第二轮复习中的运用[J]．课程教材教学研究，2008(33/34)：63-64.