证据理论融合结果的一种决策方法

吕现钊，李文艺

宿州学院机械与电子工程学院，安徽宿州，234000



证据理论融合结果的一种决策方法

吕现钊，李文艺

宿州学院机械与电子工程学院，安徽宿州，234000

针对证据理论融合结果的决策问题，给出了利用pignistic概率距离进行决策的方法。首先把决策目标转化成为对应的证据模型，然后计算融合结果与决策目标之间的pignistic概率距离，最后利用距离最小的方法进行决策。仿真实验表明该方法能够较好地解决证据理论融合结果的决策问题。

信息融合；证据理论；pignistic概率

证据理论又称为D-S证据理论，是一种不确定信息表示与处理的方法，目前该方法在多个领域都有所应用[1-3]。证据理论能够把非确定性的信息进行融合，在融合的过程中信息能够得到加强，融合结果更加有利于进行决策[4-5]。针对信息融合的结果决策问题，目前采用的方法有以下几种：采用最大mass函数方法进行决策；采用最大化或函数方法进行决策；把mass函数转化为概率然后再利用最大化概率方法进行决策[6-7]。针对证据理论的决策问题，本文采用pignistic方法[8]对融合结果进行决策。首先需要把决策目标转化为对应的证据模型，然后计算证据融合结果与决策目标的pignistic距离，利用pignistic距离最小的方法进行最终的决策。实验结果表明，该方法能够较好地完成证据融合结果的决策任务。

1 基本理论

1.1 证据理论

设Θ中的元素是互斥且有限的，Θ包含问题的所有可能，则Θ称为识别框架。Θ的幂集记为2Θ，m是2Θ到[0,1]的映射，即m:2Θ→[0,1]，称m为基本概率赋值函数(BPA)，又称为mass函数。若A∈2Θ，m应当满足以下三个条件：

(1)m(∅)=0

(2)0≤m(A)≤1,A⊆Θ

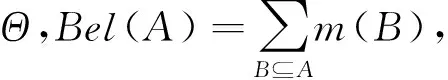
假设m1、m2为识别框架Θ下两个相互独立的基本概率赋值函数，可以利用Dempster合成公式对m1、m2进行合成，Dempster合成公式如下：

1.2 pignistic概率

设Θ为辨识框架，2Θ为Θ的幂集，R为2Θ的一个集类，A是Θ的子集，满足：

则称BetPm(x)为Θ上的pignistic概率[5]。由上式可得：

2 基于pignistic概率距离的融合结果决策

利用pignistic概率距离法进行决策之前需要把决策目标转换成对应的证据理论模型，然后计算融合结果和决策目标之间的pignistic概率距离，最后才能利用pignistic距离最小法进行决策。

设Θ={A1,A2,…,An}为辨识框架，m是多个证据融合结果的mass函数，利用最小pignistic距离决策步骤如下：

Step 1 确定出决策目标对应的证据模型。决策目标A1,A2,…,An对应的证据模型分别为m1,m2,…,mn，表达式如下：

m1(A1)=1;m1(C)=0 (C⊆Θ,且C≠A1)

m2(A2)=1;m2(C)=0 (C⊆Θ,且C≠A2)

……

mn(An)=1;mn(C)=0 (C⊆Θ,且C≠An)

Step 2 分别计算融合结果m与m1，m2,…，mn之间的pignistic概率距离，记为：d1,d2,…,dn。

Step 3 求出所有pignistic距离中的最小值。

dj=min{d1,d2,…,dn}

Step 4 根据最小pignistic距离进决策。若dj为所有pignistic距离中的最小值，则Aj为最终的决策结果。

3 仿真实验

假设辨识框架Θ={A,B,C,D}，有5组融合结果的BPA函数值如表1所示。

表1 5组融合结果的BPA值

对表1中的5组证据分别采用最大BPA函数决策方法、Smet决策方法和本文提出的决策方法进行仿真实验，实验结果如表2所示。

表2 各种决策方法实验结果比较

注：表2中“-”由该证据不能正确决策。

由表2可知，采用最大BPA决策方法时，第1组和第4组实验的决策结果分别为A和C，其他各组不能进行决策。在第2组实验数据中m(A)=m(C)=0.3，采用BPA决策方法不能对A和C进行取舍，所以该方法不能对第2组融合结果决策。同理，在第3组数据中m(B)=m(D)=0.3，采用最大化BPA方法亦不能完成决策。在第5组融合结果中m(A)=m(B)=m(C)=m(D)=0，不能利用最大化BPA方法对该组融合结果的数据决策。采用本文方法与Smet方法对各组均可以进行决策。由实验结果可以看出，决策的结果符合人们的直观认识；同时也可以看出，当采用最大化BPA方法不能进行决策时，本文所提出的最小化pignistic距离方法依然能够得到符合常理的决策结果。

4 结 论

本文对证据理论融合结果的决策问题进行了论证，给出了一种采用pignistic概率距离进行决策的方法，文中对决策方法给出了算法的详细步骤，最后采用最大化BPA决策方法、Smet决策方法和本文方法对5组融合结果进行了决策。实验结果表明，该方法与Smet方法的决策结果是相同的。

[1]付耀文,杨威,庄钊文.证据建模研究综述系统[J].工程与电子技,2013,35(6):1160-1167

[2]徐从富,耿卫东,潘云鹤.面向数据融合的DS方法综述[J].电子学报,2001,29(3):393-396

[3]史辉,曹闻,朱述龙,等.证据理论在最优路径规划中的应用[J].计算机工程与应用,2009,45(26)：213-215

[4]史超,程咏梅,潘泉.基于直觉模糊和证据理论的混合型偏好信息集结方法[J].控制与决策,2012(8):1163-1167

[5]王云飞,李辉,李云彬.利用模糊推理的证据理论信息融合算法[J].计算机工程与应用,2010，46(36):144-146

[6]Smets P,Kennes R.The transferable belief model[J].Artificial Intelligence,1994,66(2):191-234

[7]韩德强,杨艺,韩崇昭.DS证据理论研究进展及相关问题探讨[J].控制与决策,2014,29(1):1-11

[8]陈圣群,王应明.基于Pignistic 概率距离的最优证据合成法[J].信息与制,2012,42(2):213-217

(责任编辑：汪材印)

10.3969/j.issn.1673-2006.2015.09.026

2015-03-20

宿州学院硕士科研启动基金项目“多电平高压变频器矢量控制技术研究”(2009yss07)。安徽省高等学校省级优秀青年人才基金重点项目“生产车间碳足迹优化控制方法研究”(2013SQRL084ZD)。

吕现钊(1983-)，安徽宿州人，硕士，助教，主要研究方向：电力电子、电力传动。

TP391

A

1673-2006(2015)09-0095-02