考虑船舶排放的班轮公司船队部署研究

杨 斌，饶明君，朱小林，许波桅

(上海海事大学 物流研究中心，上海 201306)



考虑船舶排放的班轮公司船队部署研究

杨 斌，饶明君，朱小林，许波桅

(上海海事大学 物流研究中心，上海 201306)

针对集装箱海运中船舶排放、船队部署问题，分析了班轮运营总成本的构成，依据班轮远洋多港挂靠循环航线特征及集装箱转运特点，以可变船舶航速为决策变量，船舶运营总成本与船舶排放量最小化为目标，建立了基于低碳经济下的班轮公司船队部署多目标混合整数非线性规划模型，并引用了多目标递推算法进行求解。算例中通过对航行速度的灵敏度与帕累托分析，发现了船舶最低排放的航行速度。其次，运用航运轴辐式网络的特点，从众多港口中选择部分枢纽港进行转运形成干线运输规模效应。结果表明：该模型可以同时决策船队部署和集装箱转运，其优化结果更符合实际情况，对航运市场供需平衡的运力配置决策具有借鉴意义。

交通运输工程；船队部署；排放；帕累托分析；多目标规划

0 引 言

班轮船队部署是船公司在营运中经常面临的一类决策，其目的是合理地将班轮船队中不同类型、不同吨级的船舶部署到不同航线上，以保证船公司在此部署下取得良好的经济效益。但在实际工作中，当船型及航线较多时，则有相当一部分船队部署工作是船公司调度人员凭自己的工作经验来进行，很难保证做到最合理的部署。杨秋平等[1]为了提高船舶资源配置的适用性，建立了以船队总营运收益最大为目标的航线配船与船队规划模型；赵刚[2]研究如何最合理地将班轮公司船队中不同类型的船舶配置到公司经营的各条航线上，使整个船队取得良好的经济效益。

随着全球温室效应的加剧，各国专家学者越来越关注船舶排放对环境的影响，所以在集装箱班轮船队部署研究中，需要纳入船舶排放对海洋环境污染的影响。K-H.Lai等[3]阐述了绿色低碳航运在航运界的概念、采用和影响，帮助班轮公司保护海洋环境，寻找合适的优化方法来减少对航运环境污染。T.E.Notteboom等[4]研究集装箱班轮运输在高燃油成本背景下的班轮服务配置问题，构建了一个成本模型来模拟燃油价格波动对班轮运营成本的影响。Qi Xiangtong等[5]基于码头作业时间的不确定性，通过优化班轮船期表，使班轮在运输航线上的总燃油消耗量减少。J.Hulskotte等[6]通过制定合理的港口泊位-岸桥协同计划，使得船舶在港期间的废气排放量降低。

集装箱转运即安排船舶在任何一个枢纽港口进行卸箱、装箱、中转操作。杨秋平等[7]研究了集装箱直达运输的班轮船队规划。然而现实情况下港口分散在世界各地沿海口岸，班轮公司很难为每一对港口之间提供直达运输服务，非直达港口间的集装箱运输可以通过转运来完成，集装箱转运使得班轮公司运作上具有灵活性，但同时对船队的部署也提出了新的挑战，比如港口之间的季节性需求波动时，就需要动态调整班轮航线的部署计划。宋若辰等[8]研究集装箱空箱在途库存成本控制问题。N．K．Tran[9]主要解决运输途中挂靠港选择、挂靠顺序优化、集装箱转运等三个问题；Wang Shuai’an 等[10]研究集装箱班轮转运及航线对船舶类型选择问题。但以上研究均未考虑船舶排放对班轮公司运营及海洋环境及影响。

上述模型与方法主要以船队盈利或节省成本为优化目标，忽略了船舶航速及排放的影响，将问题简单地处理为线性模型。笔者采用Du Yuquan等[11]提出的船舶排放计算公式，作为衡量船舶排放量的目标函数，建立以周计划内船队运营总成本和船舶排放量最小化的多目标混合整数线性规划(multi-objective mixed integer linear programming)模型，通过以航行速度为决策变量，建立船舶排放和船队部署之间的关系，实现减少船舶排放量的同时降低船队部署运营成本目的。此外，为班轮公司决策每条已知航线上航行的船舶类型和数量，以及提供了船队中每种船舶类型的租用和出租数量参考，进而调整集装箱班轮转运航线，最终实现船舶排放、船队部署与集装箱转运系统优化。

1 问题描述

温室效应的时代，各行各业都要求节能减排，在船舶作为能耗大户的背景下，研究船舶节约能源消耗，降低船舶排放具有重要的现实意义。船舶油耗与船舶速度有关，单位时间的油耗rF主要由船舶速度s决定，油耗与船舶速度成正相关，而船舶类型也决定航速的高低。在Du Yuquan等[11]的研究中，单位时间里的油耗由式(1)确定：

rF=c0+c1·sμ

(1)

式中：rF为单位时间里的油耗；s为船舶速度；c0，c1为回归系数；μ的值与船舶大小型号有关。

每条航线的船舶油耗由式(2)确定：

(2)

式中：Fr为每条航线r的船舶油耗，可以用单位时间里的油耗乘上航行时间来表示；mr表示航线r的里程；sr表示航行在航线r上的速度；μr表示航行在航线r上的船舶系数。

为了呈现油耗和速度之间的关系，对式(2)的速度求1阶导数和2阶导数：

(3)

(4)

(5)

式(6)用来计算船舶v在航线r航行期间排放，记为hr,v：

hr,v=∑r,n[Fr·EFr,n]

(6)式中：Fr为船舶在航线r上航行期间的油耗量，kg；EFr,n为航线路径r上的第n个排放因素计算系数，目前主要考虑的排放因素为CO2，NOX，SOX。如表1。

以某全球集装箱班轮运输公司作为研究对象，运营一组固定班轮航线，定期服务于一组港口。图1为具有3条路径的班轮航线网络。

图1 具有3条路径的班轮航线网络Fig.1 Liner shipping network with three ship routes

根据实际情况，假设每条班轮航线保持每周班次和船舶一起部署各航线上，并且在远洋多港挂靠循环航线中，每一个港口可以由航行期间服务于航线的船舶停靠一次以上。对所有港口进行编号，使得每条航线就可以用数字表达，每条航线上数字的个数代表挂靠港口的总次数，用Nr表示。例如在航线1中，一共有3个港口，那么Nr=3，对应港口挂靠顺序见式(7)。

Pr1→Pr2→Pr3→Pr1

(7)

2 模型的建立

首先定义相关集合、参数与决策变量。

1)集合变量：r∈R表示船舶航线集合；p∈P表示港口集合；v∈V表示船舶类型集合；Nr表示航线r靠泊的港口数量；τr={1,2，…，Nr}表示航线r上港口停靠顺序序列(i∈τr)。

集装箱在港口进行装卸操作可以分为三类：第1类是集装箱从该港口装箱，运往其他港口；第2类是集装箱来自其他港口，在该港口卸箱；第3类是集装箱在该港口进行转运操作。中转港口进行转运的集装箱数量计算式(8)：

(8)

2.1 数学模型

船队运营中的主要成本有5项，其次还有一项收益，如表2。

表2 各项成本和收益

以周计划内船队运营总成本和排放量最小，建立与船舶航行速度有关的混合整数非线性规划多目标模型。固定的班轮航线里程已知，船航行速度决定船舶在该条航线的航行时间，将航行时间代入模型中，以满足周计划集装箱运输需求：

(9)

(10)

Where

(11)

(12)

(13)

(14)

(15)

(16)

s.t． ∑vxr,v=1,∀r∈R

(17)

(18)

(19)

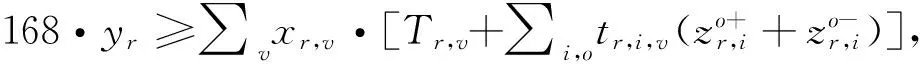
(20)

(21)

(22)

(23)

(24)

(25)

(26)

(27)

目标函数式(9)与式(10)分别定义周计划内船队运营总成本与船舶总排放量；式(11)～式(16)表示船队运营总成本的组成；约束条件式(17)表示每条航线上只能部署同一类型船舶；式(18)表示v型船舶在航线r上的航行时间；式(19)表示可租用船舶的数量限制；式(20)确保分配的船舶数量能够满足集装箱运输需求；式(21)表示每条航线各航段的运载量不能超过船舶容量限制；式(22)集装箱运输数量在航线的各个航段之间流量守恒约束；式(23)确保港口之间的运输需求得到满足；式(24)表示来自港口o的集装箱不能运回港口o；式(25)表示港口o运往其他港口的集装箱不会在港口o卸箱；式(26)表示船舶租用和出租数量的守恒方程；式(27)表示在航线r上船舶航行的航速区间限制。

2.2 非线性转换

(28)

(29)

约束函数式(17)～式(27)：

yr,v≤M1·xr,v,∀r,v

(30)

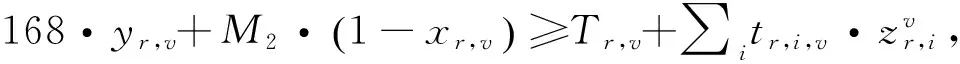
(31)

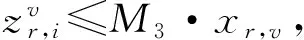
(32)

(33)

(34)

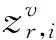
3 多目标求解算法

通过对非线性模型的处理，下面提出上述MOMILP模型的求解递推算法：

Step1：通过式(35)、式(36)定义的模型求各自目标函数的最优解f*和h*。

Step2：通过式(37)对f和h进行同一量纲处理，分别赋予相应权重并构造求解目标函数，以使求解结果f和h趋于各自的最优解f*和h*。对应的约束为式(17)～式(27)、式(30)～式(34)；其中：α>0，β>0，α+β=1为权重系数。取fmin=f*,hmin=h*；fmax与hmax取值基于决策者对船舶运营成本与排放量的偏好程度确定。

Step3：初始化f=f*。

Step4：求解式(37)定义模型，得到h,如果h-h*≤ε其中(ε≤hmax-h*)，则转向Step6，否则转向Step5。其中ε为班轮公司能接受的排放增加量。

Step5：放松λ值限制(即增大λ值)，取f=f*+λ其中(λ≤fmax-f*)，执行Step4。

Step6：得到f和h的满意解：

f*=min{f|(17-27),(30-34)}

(35)

h*=min{h|(17-27)}

(36)

(37)

4 算例分析

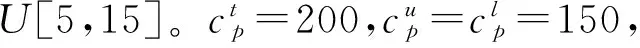
表3 不同航线相关参数

表4 班轮船队部署参数

(续表4)

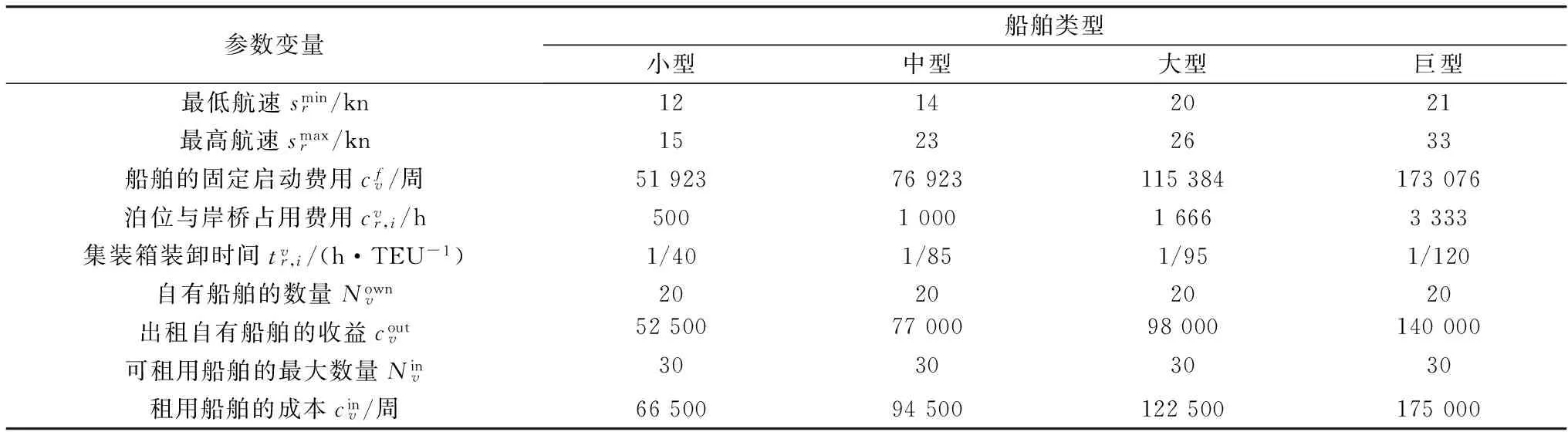
参数变量船舶类型小型中型大型巨型最低航速sminr/kn12142021最高航速smaxr/kn15232633船舶的固定启动费用cfv/周5192376923115384173076泊位与岸桥占用费用cvr,i/h500100016663333集装箱装卸时间tvr,i/(h·TEU-1)1/401/851/951/120自有船舶的数量Nownv20202020出租自有船舶的收益coutv525007700098000140000可租用船舶的最大数量Ninv30303030租用船舶的成本cinv/周6650094500122500175000

依据上述模型与算法，将相关参数输入所编写的Lingo 11.0程序进行求解。运行后，得到了班轮公司的船队部署最佳方案，如表5。从该优化结果可以看出，该班轮公司船队模型不仅可以求解出船舶部署方案，而且可以计算出船舶在各航线上航行的最佳航速。此外，该模型较全面地考虑了航速与运营成本、航速与排放、航速与航线配置之间的耦合关系，反映了船舶航速变化对船队部署的非线性影响。

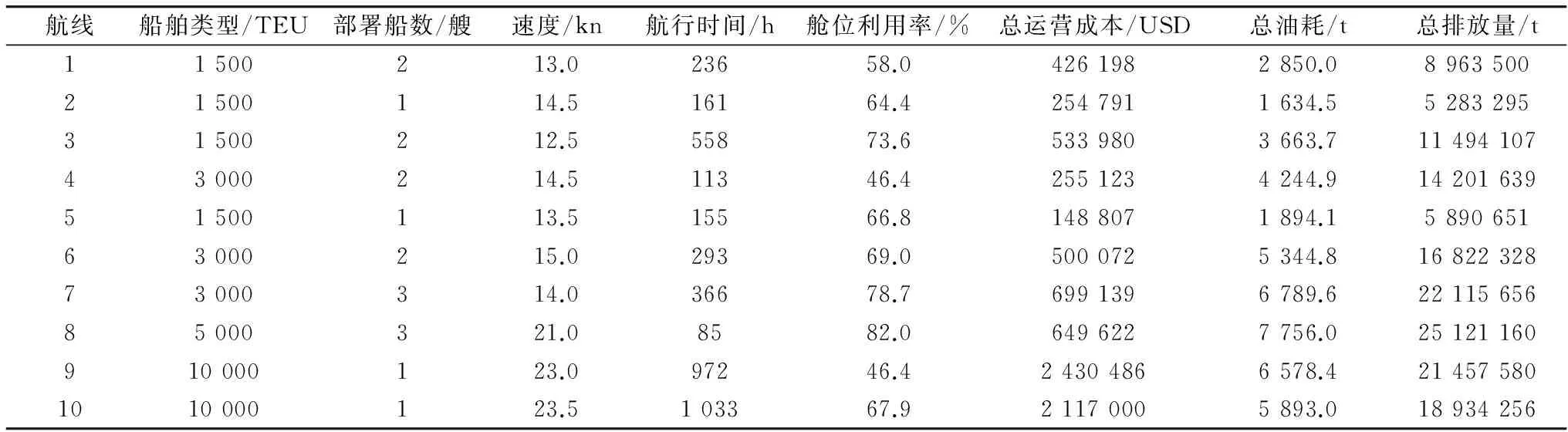
表5 程序运行结果

4.1 船舶速度的灵敏度分析

船舶速度的灵敏度由式(38)确定：

(38)

式中：Δs为船舶速度增量，分别取-25%，25%，0%，50%，75%。

运行程序得到结果如表6。

表6 灵敏度分析

从表6中可知，在船舶最低排放的速度s*基础上减速25%时，不仅使整个班轮运营总费用增加8.628%，而且排放也会增加9.281%，表明班轮公司在航运市场旺季时不会选择船舶航行速度低于最低排放的速度，而倾向于选择提速，以增加船舶污染排放为代价，来减少整个班轮网络的运营总成本。当船舶速度增加50%时，fCB的增量为负，表明港口靠泊成本降低，因为由表4可知中型船舶的单个集装箱装卸作业时间减少，虽然集装箱转运量有所增加，但是港口岸桥作业的总时间减少了，所以相应的港口靠泊成本降低。同时，随着船舶的不断提速，使得整个船队的船舶资源利用率也逐渐增加，从而使得班轮公司fCI费用降低。

然而，从表中可知fCT增量的百分比是最大，原因是航线2上配置的船型载重量增大，可以容纳更多的集装箱在该航线上进行转运操作，所以使得相应的转运费用增加。图2为船舶排放与航速变化关系曲线。

图2 船舶排放与航速变化曲线Fig.2 Curve of vessel’s emissions changing with different speeds

从整体来看，在航运市场旺季时，船舶提速会降低船舶运营总成本、船舶启用和航行的固定成本、租用船舶的成本等，同时增加了出租自有船舶的收益。然而，在航运市场淡季时，船公司在满足市场运力需求前提下可采取降速增加船舶航次的方案，实现整个船队的运力闲置率最低。

4.2 航线各航段的船舶运载率分析

船舶运载率是指船舶在营运中载重吨位实际利用程度的指标，通过船舶运载实际吨位与载重能力的比值衡量，其比值越大，表明船舶载重吨位利用率越高。设w为船舶在航线r上第i个航段的运载率，其效用函数由式(39)确定：

(39)

图3为航线8各航段的船舶利用率。由图3可知，在航线8的航段21→10→9港口之间，船舶载重吨位利用率最高，表明班轮公司收益最大。当运力小于运量，将会造成运输不畅；而运力大于运量，将导致运力过剩。所以，班轮公司可根据航线不同航段的运载率来合理调整船队部署，通过合理调整运力结构，实现以小型船舶进行支线港运输、以中型船舶进行中短距离运输、以大型船舶进行远距离干线运输的科学的运力格局，保持运力与运量的协调平衡，使班轮公司运力配置得到有效利用，从而降低班轮公司运营总成本，提高公司运营收益。

图3 航线8各航段的船舶利用率Fig.3 Ship utilization ratio on each leg of ship route 8

4.3 船舶航速与船队部署之间的关系分析

表7是中转港和船队部署的灵敏度分析结果。

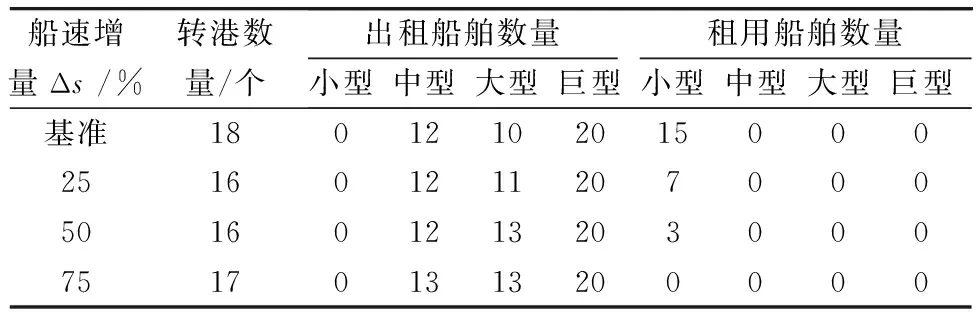
表7 中转港和船队部署的灵敏度分析

由表7可知，船舶提速改变了集装箱中转港的数量和位置，表明该模型具备动态调整转运网络能力，虽允许在所有港口进行中转操作，但是它从39个港口中选择部分港口进行集中转运，从而具有轴辐式网络的优点，降低网络运营总成本。其次，船舶提速会改变班轮船队的部署，减少船舶使用数量，降低船舶启动的固定成本。此外，该模型能根据运载量现实需求，合理调整每条路径的船舶型号，当中转港口数量和位置发生变化，会改变原有路径的集装箱流量，这就需要对船舶型做调整。

虽然小型的集装箱班轮需求量较大，班轮公司选择租用小型号的船，而不是使用自有的更大型号的船，原因是从整个班轮船队部署出发，选择出租自有其他型号的船舶，租用小型号的船舶能够带来更大的收益。班轮公司在实际的船队部署问题上，就需要充分利用好这个原理，合理选择租用和出租的船舶类型与数量，实现降低成本的目标。

4.4 船舶排放与船队运营成本的Pareto分析

基于船舶运营总成本与排放量之间的均衡关系，为使这两方面都降低到合理满意值，这需要班轮公司做出权衡，更需要港口运营者与班轮公司相互协作，调整船舶航速，合理安排泊位-岸桥分配计划，以实现双方利益的均衡优化。例如，在图4中，如果船公司采用点(h1，f1)处的船队部署计划，则相比点(h2，f2)处的计划而言，船公司减少了船舶相关运营成本，但却导致班轮公司排放量过高。

图4 船舶排放与运营成本Pareto分析Fig.4 Pareto analysis for vessel’s emissions and costs

当α=β=0.5时，此时决策者对船舶运营总成本与船舶排放无任何偏好因素。从图4可知，在航运市场运力供需平衡时，随着船舶加速，船舶运营总成本越来越小，但相应的船舶排放却上升。所以，在绿色航运越来越受到关注的背景下，班轮公司需要权衡经济效益与环境效应之间的关系，使二者达到帕累托均衡。

5 结 语

笔者从运营者角度研究集装箱班轮公司的船队部署问题，创新性地将船舶排放、船队部署及集装箱转运路径的调整进行整体优化。主要的工作和贡献包括以下三点：1)针对集装箱海运网络中的船舶排放与船队部署问题，将可变船舶航速作为决策变量，建立了基于考虑船舶排放的班轮公司船队部署决策优化模型，将非线性约束条件进行线性转换，并提出了多目标求解函数递推算法。

2)通过对船舶航速的灵敏度与帕累托分析，发现船舶航速与船队总运营成本的效益背反规律，在航运市场旺季时，随着船舶航速的不断增加，船公司会采取增加排放量的方式来减少船队总运营成本；相应在航运市场运力供需失衡时，船公司可通过降低航速增加航次的方案使运力闲置最小，并且该模型能通过可变航速策略来合理调整船队部署。

3)运用海运轴辐式网络特点，选择部分枢纽港进行集装箱转运，产生枢纽港之间的干线运输规模效应，减少班轮公司运营总成本，对未来航运市场运力供需恢复平衡的船队部署决策具有借鉴意义。

在接下来的研究中，可以从以下方面进行：①考虑各港口OD对之间的季节性货流对班轮船队部署的影响；②在运力供需失衡的背景下研究集装箱班轮船队部署，使船队运力总浪费最小；③调整船队部署以适应航运市场运价波动的情形。

[1] 杨秋平,谢新连,苏晨.航线配船与船队规划模型及算法实现[J].中国航海,2009,32(1):91-95. Yang Qiuping,Xie Xinlian,Su Chen.Model of ship routing and fleet planning and its algorithm [J].Navigation of China,2009,32(1):91-95.

[2] 赵刚.班轮航线配船模型的分析与改进[J].系统工程学报,1997,12(1):80-86. Zhao Gang.Analysis and improvement on the vessel allocation model of liner service [J].Journal of Systems Engineering,1997,12(1):80-86.

[3] Lai K-H,Lun VY,Wong CW,et al.Green shipping practices in the shipping industry,conceptualization adoption and implications [J].Resources,Conservation and Recycling,2011,55(6):631-638.

[4] Notteboom T E,Vernimmen B.The effect of high fuel costs on liner service configuration in container shipping [J].Journal of Transport Geography,2009,17(5):325-337.

[5] Qi Xiangtong,Song Dongping.Minimizing fuel emissions by optimizing vessel schedules in liner shipping with uncertain port times [J].Transportation Research Part E:Logistics and Transportation Review,2012,48(4):863-880.

[6] Hulskotte J,van der Denier.Fuel consumption and associated emissions from seagoing ships at berth derived from an on-board survey [J].Atmospheric Environment,2010,44(9):1229-1236.

[7] 杨秋平,谢新连,裴光石.班轮运输船队规划模型与仿真[J].西南交通大学学报,2011,46(6):1046-1054. Yang Qiuping,Xie Xinlian,Pei Guangshi.Modeling and Simulation of Fleet Planning for Liner Shipping [J].Journal of Southwest Jiaotong University,2011,46(6):1046-1054.

[8] 宋若辰,赵一飞.班轮公司集装箱空箱在途库存控制研究[J].重庆交通大学学报:自然科学版,2012,31(4):890-894. Song Ruochen,Zhao Yifei.Study on liner operators’ controlling of empty containers’ in-transit inventory [J].Journal of Chongqing Jiaotong University:Natural Science,2012,31(4):890-894.

[9] Tran N K.Studying port selection on liner routes：An approach from logistics perspective [J].Research in Transportation Economics,2011,32(1):39-53.

[10] Wang Shuai’an,Meng Qiang.Liner ship fleet deployment with container transshipment operations [J].Transportation Research Part E:Logistics and Transportation Review,2012,48(2):470-484.

[11] Du Yuquan,Chen Qiushuang,Quan Xiongwen,et al.Berth allocation considering fuel consumption and vessel emissions [J].Transportation Research Part E:Logistics and Transportation Review,2011,47(6):1021-1037.

Fleet Deployment of Liner Ship Company Considering Vessel’s Emissions

Yang Bin, Rao Mingjun, Zhu Xiaolin, Xu Bowei

(Logistics Research Center, Shanghai Maritime University, Shanghai 201306, China)

Aiming at the problems of vessel’s emissions and liner ship fleet deployment in container shipping system, the composition of total liner operation costs was analyzed. According to the features of cycle multi-port call route in ocean liner service, as well as the characteristics of container transshipment, a multi-objective mixed integer nonlinear programming model for liner ship company fleet deployment was established with the objective of minimizing total costs of liner operation and emissions, which was based on the low-carbon economy on the premise that vessel’s speed was made as decision variables. And then the multi-objective recursive algorithm was applied to solve the function. The sensitivity analysis of sailing speed and Pareto were analyzed in case studies, the lowest emissions speed was discovered. Moreover, making use of the features of shipping hub and spoke network, hub pots were chosen from many parts to generate scale economies. Result indicates that the proposed model can simultaneously develop fleet allocation and container transshipment and its optimization result accords with the actual condition, which is referential for the vessel capacity decision for the supply and demand balance of shipping market.

transportation engineering; fleet deployment; emissions; Pareto analysis; multi-objective programming

10.3969/j.issn.1674-0696.2015.05.24

2014-05-19；

2014-08-13

国家自然科学基金项目(71171129)；上海市科委科研计划项目(12510501600；11510501900；12dz1124802；14DZ2280200)

杨 斌(1975—)，男，山东青岛人，教授，博士，主要从事绿色航运物流系统方面的研究。E-mail: binyang@shmtu.edu.cn。

U692.2+1；F550.81

A

1674-0696(2015)05-120-06