基于地震要素的能量传导对桥梁的作用分析

唐 琳，肖盛燮，韦良文

(重庆交通大学 土木工程学院，重庆 400074)



基于地震要素的能量传导对桥梁的作用分析

唐 琳，肖盛燮，韦良文

(重庆交通大学 土木工程学院，重庆 400074)

分析了地震波在地下岩层中的传播路径、传递过程中能量的耗散以及在不同介质间传递时能量的损失，讨论了基于地震强度、震源深度、震中距等地震要素的能量对桥梁的作用，得出了反应能量与地震惯性力的关系式；分析了不同地震要素对能量的影响和变化趋势，提供了地震能量通过介质载体传导对桥梁的地震作用的分析途径。

桥梁工程；地震要素；能量传导；变化趋势

地震是一种常见的地质灾害，也是人类面临的最主要和最严重的自然灾害之一。据统计，地球上每年约发生500多万次地震，即每天要发生上万次地震。其中绝大多数太小或太远以至于人们感觉不到；真正能对人类造成严重危害的地震大约有一二十次；能造成特别严重灾害的地震大约有一两次。我国位于世界两大地震带—环太平洋地震带与欧亚地震带之间，受太平洋板块、印度板块以及菲律海板块的挤压，地震断裂带十分发育。

对桥梁而言，地震所带来的破坏，无论从数量上还是程度上，都远远超过其他自然灾害，会对人类生命和财产安全造成巨大的损失。笔者拟通过对地震强度、震源深度、到震中水平距等地震要素反应地震能量在简单地质状况条件下的传导和耗散关系以期得到地震对桥梁的动力破坏作用。

1 地震震级能量和烈度

地震震级是衡量地震大小的一种量度，每一次地震只有一个震级；它是根据地震时释放能量的多少来划分的。震级可以通过地震仪的记录计算得到，震级越高，释放的能量也越多。我国使用的震级标准是国际通用震级标准，叫里氏震级M。在里氏震级M及其释放的能量E之间有如下的近似关系：

lgE=11.8+1.5M

(1)

由式(1)可得：

E2/E1=101.5(M2-M1)

(2)

由式(2)可以看出，每当地震的震级提高1级，它释放的能量将提高约31.6倍。地震的震级提高2级，那么它释放的能量将提高约1 000倍。所以地震的震级越高，释放的能量越大，对各种建筑结构和人类的生命安全造成的损失越大。

地震的烈度是指地震所造成的地面和建筑结构的破坏程度。影响烈度的因素有震级、震源深度、震中距、地表空间状况和地层构造等。按JTG/T B 02-01—2008《公路桥梁抗震设计细则》[1](以下简称《细则》)规定，抗震设防烈度为Ⅵ度及以上地区的公路桥梁，必须进行抗震设计。

2 地震波的传播路径

地震是强烈的波动作用在介质中传播[2]，在地下岩层中，均匀的各向同性介质是很难遇到的。地震波在不同介质中具有不同的速度，它传播路径是由其在地下传播速度的分布来决定的。由费马原理可知，波传播始终遵循最小时间路径的原则。因此，地震波只有在均匀介质中传播时，其空间最短距离也是其时间最短距离。在不均匀介质中传播速度的分布使得最短空间距离并不是最短时间路径。图1比较了在同一种介质中恒定波速的传播路径和线性增大波速的传播路径。可见，由于速度的不断变化会使得地震波在传播方向上的最小时间路径也产生不断变化。

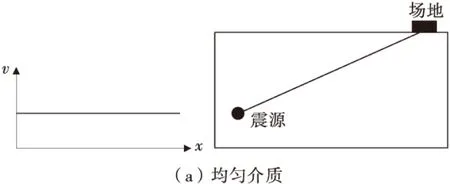
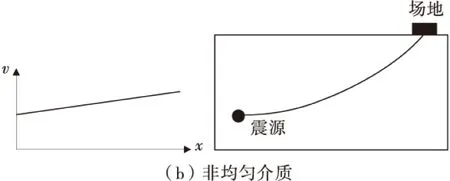
图1 均匀与非均匀介质中传播路径比较Fig.1 Comparison of paths in uniform and non-uniform medium

假设当地震波在介质中以线性增大的波速传播时，即地震波的波速为v(x),地震的震源深度为z，震源到场地的水平直线距离为x，如图2。则可以通过下列的计算得到其传播路径的实际距离。

图2 非均匀介质中的传播距离Fig.2 Propagation distance in non-uniform medium

取微小地震波传播路径单元dx，将dx视为直线，则由斯奈尔定理可得：

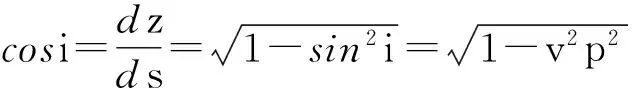
对上式积分，即可得地震波的实际转播路径的长度s：

(3)

则地震波从震源传到场地所需要的时间为：

(4)

式中：v为地震波传播速度；p为射线参数；i为入射角；s为实际传播距离；T为实际传播时间。

由式(3)和式(4)可以看出，地震波的实际传播路径和传播时间与震源深度、水平距离和地震波的传播速度有关。

3 地震波能量的耗散

地震波作为波的一种，既可以在地下介质中传播，也可以在空气介质中传播。由于空气只能受压缩而不能受剪切，因此在空气中只有P波可以传播，而S波不能传播。

当地震波在地下介质中传播时，由于介质的非均匀性使地震波的能量随着它在地下的传播过程会不断的衰减。这种衰减会受到饱和度、频率、温度、孔隙度、压力、应变振幅大小、岩石特性[3]以及传播距离等因素影响。

由结构动力学可知，某一质点在介质中随时间变化的振幅方程为：

(5)

如果将介质视为完全均匀、各向同性的弹性介质，那么该质点在经过时间t后的振幅大小与距该质点时间距离为t的另一质点振幅大小一致。这样便可以得到在该介质中沿地震波传播方向上任意一点的振幅方程：

(6)

式中：s为到震源的距离；v为地震波波速。

由能量与振幅的关系式

(7)

可得到在均匀介质中地震波传递距震源距离为s后的能量大小。

除此之外，当地震波传递到具有不同传播速度的介质分层截面时，由于折射、透射以及地震波类型转换的原因，也会发生能量的改变。地震波在分层截面的能量分布通常由反射系数R和透射系数T来表示。这些系数通过入射波的大小也就是它的振幅或者能量与反射波和透射波的大小之间比值来确定，它们的大小取决于介质密度和地震波在该介质中的传播速度。这里引用波抗阻的概念：岩石的波阻抗为岩石中的纵波速度与岩石密度乘积，表明应力波在岩体中传播时，运动着的岩石质点产生单位速度所需的动力，反映了岩石对动量传递的抵抗能力。其表达式为：

I=ρv

(8)

式中：I为波抗阻；ρ为介质密度；v地震波的波速。

常见岩石的动力参数如表1。

表1 常见的不同基岩动力参数

反射系数与透射系数除了与地震波波速和介质的密度有关外，入射角度也会影响两个系数的大小。假设地震波是垂直入射，通过对佐普瑞兹方程求解，就可以得到反射系数和透射系数计算式如下：

(9)

(10)

当地震波以一定入射角度传递时，不同入射角度也会影响两个系数的大小；同时由于界面上下介质不同，地震波会产生波的分裂和转化，即反射波P1和PS1、透射波P2和PS2，如图3。介质1的速度和密度均大于介质2的速度和密度，即I1>I2。

图3 地震波的反射与透射Fig.3 Reflection and transmission of seismic waves

在对佐普瑞兹方程求解的过程中需要特别注意分层界面的边界条件。图4为地震波传递到在上下层介质的速度比为0.5、密度比为0.8时，不同入射角度的反射系数与透射系数的关系。

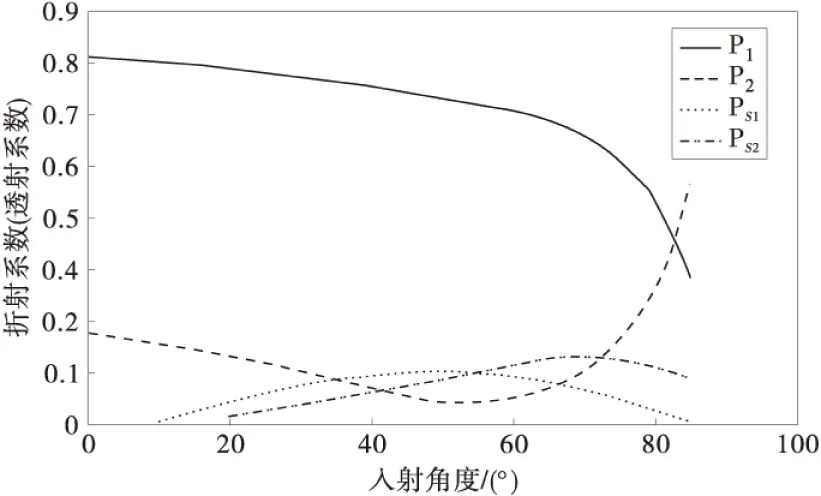
图4 R，T与角度的关系Fig.4 Relationship of R,T and the angle

当地震波传递到分层界面时，一部分能量会随着透射波传递到下一层的介质中，一部分能量会因为反射波而滞留在原介质中。

滞留的能量与总能量的比值称之为能量的滞留比w，其计算式如下：

(11)

4 地震对桥梁的影响

地震对桥梁的危害与结构形式、体系布置以及抗震构造等有着很大关系。另外，桥梁的危害在很大程度上还取决于桥址的地基条件[5]。在地震影响范围内的任何一个点上始终都会有3个加速度分量同时出现。因为任何一座桥梁对竖直方向的荷载都是有设计的，并且竖直加速度的分量往往只有水平加速度分量的1/2甚至更少。因此来自于竖向的加速度对于横向延伸的桥梁来说没有太大的影响，水平加速度具有更加明显的意义，因此地震荷载通常建模为简单的剪切而不是三轴压缩[6]。

对于完全刚性结构来说，其完全和场地承受一样的水平运动。由于桥梁并不是完全刚性结构，所以桥梁和场地在运动的过程中并不是完全一致的，除了伴随着场地振动外，还会有一个相对于地基的附加振动。特别是跨越断层地带、液化地基的桥梁，场地相对位移是发生落梁破坏、支座剪切、梁和墩(台)的结构损伤等地震破坏的主要原因[7]。桥梁的上部结构在地震的过程中并不会直接受到地震的影响。桥台和基础的运动带动着桥墩的振动，桥墩再将惯性力传递到上部结构中，从而引起整座桥梁的振动。下部结构和基础的严重破坏是引起桥梁倒塌、并在震后难以修复使用的主要原因，它是由于振动产生的惯性力引起的破坏[8]，地震波使桥梁结构发生纵、横向振动，使结构的内力和变形突然大幅度增加，导致结构破坏[9]。

桥台的振动是由地震波传递到桥梁基础时所携带的能量和由能量产生的惯性力所引起。根据所有力做功与能量相等的这个前提条件，地震能量与惯性力的关系可以通过式(12)来表示：

E=FxDx+FyDy+WDz+fzDz

(12)

式中：Fx为水平惯性力在x方向的分量；Dx为桥台水平位移在x方向的分量；Fy为水平惯性力在y方向的分量；Dy为桥台水平位移在y方向的分量；W为基岩土自重；Dz为水平位移在z方向的分量；fz为z方向上基础与土体之间的摩擦力。

由此，通过式(1)～式(11)的一系列计算，便得到在已知地震要素的前提下，桥台处地震波传导的能量与桥台所受惯性力的关系，如式(12)。通过此关系式，如果测得桥台的位移，就可以得到在地震影响范围内的桥梁受到惯性力的大小。

5 算 例

假设某震级为6级的地震，其震源距地面约为50 km；为简化计算，假设其地质情况为上下两层各25 km，如图5。

图5 地震波传播示意(单位:km)

介质1的参数为ρ1=2.8 g/cm3，vp1=6 km/s，vs1=3.47 km/s，入射P波的角度为i，刚度k=1.2×106N/mm，周期T1=15 S；介质2的参数为ρ2=2.24 g/cm3，vp2=3 km/s，Vs2=1.73 km/s，入射P波的角度为h，刚度k=1.0×106N/mm，周期T2=8 s，将两层介质均视为各向同性的均匀介质，即最短空间距离与最短时间距离相同，并假设初始相位角为0。距震源水平距离200 km处有一钢筋混凝土梁桥，地震波传递方向与桥梁行车方向成30°夹角，基岩自重为1.5×103kN，基础与土体之间的摩擦力为800 kN。

地震震级为6级，由式(1)可得其震源处的能量大小为：

E0=e11.8+1.5×6=1.08×106(kJ)

由几何关系可得：

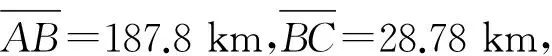
则地震波从A点传到B点和从B点传到C点的时间分别为：

则经历时间tAB后，在B点的振幅由式(5)可得：

x=1.34×e-0.042×31.3×cos(0.42×31.3)=0.35(m)

将x=0.35 m带入式(7)，便可以得到B点处的能量大小E为：

由式(11)可得，当地震波由介质1传递到介质2时的能量滞留比为：

1.452×0.034)=0.75

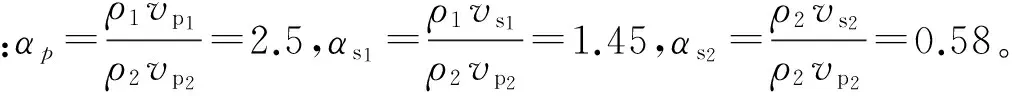
由图4可得：Rp=0.48，Rs=0.14，Tp=0.25，TS=0.03，能量衰减比S=0.6。

则传递到介质2的能量大小为：

E2=E1·(1-w)=7.35×104·(1-0.75)=1.8×104(kJ)

当地震波传递到介质2后，重复上述步骤，可以求得地震波传递到C点，也就是桥梁所处的位置时的能量大小为：

E3=4.0×103(kJ)

假设桥台在地震发生之后的水平x方向位移为30cm，y方向位移为40cm，竖直z方向位移为20cm，则地震惯性力大小由式(12)有：

4.0×103=sin30·F×0.3+sin60·F×0.4+

1 500×0.2+800×0.2

解得：

F=7 131(kN)

6 不同地震要素对能量的影响

在不同的地震要素条件下，能量的变化趋势是不同的，笔者计算了不同震级、震源深度和水平距离对能量的影响，并得出结果如表2。

表2 不同要素对能量的影响

Table 2 Affect of different elements for energy /103kJ

由表2可以得出如下结论：

1)地震震级的改变对能量的影响最大。当震级比较小的时候，随着震级的增加，传递到桥梁处的能量增幅也较小，当地震震级>6级时，能量的增幅明显的增大，因此，当地震>6级时，对桥梁进行抗震和防震的保护措施就非常有必要，这也正好符合《细则》中对桥梁抗震设计的要求。

2)在均匀介质的条件下，如果地震震级和水平距离恒定，那么传递到桥梁处的能量会随着震源深度的增加而线性的减小，其变化趋势为，震源深度越大，能量减小的幅度越小。

3)在均匀介质的条件下，如果地震震级和震源深度恒定，那么传递到桥梁处的能量会随着水平距离的增加而几乎呈直线的减小。随着水平距离的减小，能量增加的幅度明显变大。

值得注意的是，笔者的算例是考虑理想状况下的简单地质情况，鉴于实际地质情况的复杂多变性，较为精确的计算还需要进一步的研究和探索。

7 结 语

通过地震能量传导规律分析，为地震能量通过介质载体传导对桥梁的动力破坏作用分析提供了途径。在已知地震要素的前提下能量对桥梁的作用，得出了简单分层地质情况下能量和桥梁所受地震惯性力的关系式，分析了不同地震要素对能量传递以及能量通过介质载体对桥梁作用的变化规律。对桥梁选址、防震和抗震都有一定的借鉴意义。

[1] JTG/T B 02-01—2008公路桥梁抗震设计细则[S].北京:人民交通出版社,2008. JTG/T B 02-01—2008 Guidelines for Seismic Design of Highway Bridge[S].Beijing: China Communications Press,2008.

[2] 肖盛燮,陶庆东.地震海啸驱动方向和破坏力探讨 [J].重庆交通大学学报:自然科学版,2012,31(1):90-93. Xiao Shengxie,Tao Qingdong.Mystery of earthquake-induced tsunami [J].Journal of Chongqing jiaotong University:Natural Science,2012,31(1):90-93.

[3] 李振春,王清振.地震波衰减机理及能量补偿研究综述[J].地球物理学进展,2007,22(4):1147-1152. Li Zhenchun,Wang Qingzhen.A review of research on mechanism of seismic attenuation and energy compensation [J] .Progress in Geophysics,2007,22(4):1147-1152.

[4] 邓巧琳.地震波在反射与透射影响下的能量衰减分析[D].长沙:湖南大学,2013. Deng Qiaoling.Derivation of Reflection and Transmission Coefficients of Seismic Waves in Viscoelastic Media[D].Changsha:Hunan University,2013.

[5] 刘春,刘长宏,宋俊杰.地震对桥梁的危害、抗震措施以及结构振动控制[J].北方交通,2011(11):59-60. Liu Chun,Liu Changhong,Song Junjie.Earthquake damage to bridge,aseismatic measures and structural vibration control[J].Northern Communications,2011(11):59-60.

[6] Technik,Organisation,Wirtschaftlichkeit.Handbuch für Bauingenieure[M].Heidelberg :Springer-Verlag,2011:1547-1548.

[7] 谢旭.桥梁结构地震响应分析与抗震设计[M].北京:人民交通出版社,2006. Xie Xu.Seismic Response and Design of Bridge[M].Beijing: China Communications Press,2006.

[8] 肖盛燮.桥梁承载力演变理论及其应用技术[M].北京:科学出版社,2008:130-131. Xiao Shengxie.Carrying Capacity Evolution Theory of Bridge and Application Technology[M].Beijing: Science Press,2008:130-131.

[9] 肖盛燮.灾变链式演化跟踪技术[M].北京:科学出版社,2011. Xiao Shengxie.Evolution of Catastrophic Chain and Tracking Technology [M].Beijing: Science Press,2011.

Analysis of Energy Transfer on Bridges Based on Seismic Elements

Tang Lin, Xiao Shengxie, Wei Liangwen

(School of Civil Engineering,Chongqing Jiaotong University，Chongqing 400074，China)

The seismic wave transfer path in the subterranean and energy dissipation in the process of transfer as well as the energy loss passing between different media were analyzed.The effect of the energy of earthquake elements,including the seismic intensity,focal depth and the distance of the epicentre,on the bredge was discussed.The relational expression between response energy and the force of seismic inertia was obtained.And the effect and changing trends of different seismic elements on the energy were analyzed,which provided the analysis approach that the seismic energy transferring through the medium could exert seismic effect on the bridge.

bridge engineering; seismic elements; energy transfer; changing trends

2014-10-08；

2014-10-30

国家自然科学基金项目(50879097)

唐 琳(1982—)，男，四川南充人，工程师，主要从事桥梁工程和防灾减灾方面的研究。E-mail:tang_527@126.com。

10.3969/j.issn.1674-0696.2015.05.01

U442.5+5

A

1674-0696(2015)05-001-04