考虑砌体本构关系的石拱桥极限承载力研究
郑 丹,黄才政
(重庆交通大学 河海学院,重庆 400074)
考虑砌体本构关系的石拱桥极限承载力研究
郑 丹,黄才政
(重庆交通大学 河海学院,重庆 400074)
考虑砌体材料受压破坏本构关系,通过分析截面偏心受压的弯矩轴力关系,得出了拱桥破坏过程中截面偏心距的限制条件;通过非线性优化的机构分析法得出了石拱桥的极限承载力,并在此基础上讨论了砌体抗压强度对石拱桥的极限承载力的影响。结果表明:砌体材料的抗压强度较低时,石拱桥承载能力对材料强度较为敏感,且随着石拱桥跨径的增大,敏感性进一步增大。
桥梁工程;石拱桥;砌体;偏心受压;非线性优化
0 引 言
由于具有取材方便、造价低廉、超载能力强等众多的优点,石拱桥广泛应用于我国公路建设中,特别在西南地区的中小型桥梁中占比极大。在对现有公路升级改造时,经常需要对现存的大量石拱桥进行综合性能评估,以判断其使用寿命或进一步通过加固改造发挥其潜力[1]。但由于理论上尚存欠缺,在一些石拱桥设计、安全性评价方面仅是根据经验判断[2]。因此,如何采取科学、合理的理论和方法评估石拱桥的极限承载力就显得尤为重要。
对于拱桥的极限承载力的研究,传统的机构分析方法[3]假定砌体材料抗压强度无穷大并且无抗拉能力,当拱内产生足够多的塑性铰使其变成机动体系时,结构发生破坏。钱令希[4]将线性划法应用到石拱桥中,以拱圈最小厚度为目标函数, 提出了用拱圈实际厚度和最小厚度之比的拱厚安全度;陈荣刚等[5]以石拱圈极限偏心距的不超过4/9倍的拱圈厚度的经验公式为约束条件,应用极限平衡理论建立了石拱桥极限承载能力分析的模型。但这些研究均假设砌体的抗压强度为无限大,这显然不符合实际情况。实验表明石拱桥在破坏过程中,主拱圈会出现竖向裂纹,这表明确实存在砌体材料被压碎的现象[6];因此必须考虑砌体材料的受压变形直至破坏的过程,才能正确评估石拱桥的极限承载能力。F.W.Smith等[7]考虑了砌体材料的有限强度,但得出的结论为定性分析,没有定量计算砌体材料强度对拱桥承载力的影响;A.Orduna等[8]考虑砌块间的变形协调,采用离散元的方法计算了砌体材料强度对拱桥极限承载力的影响,但没有分析砌体强度影响拱桥承载力的物理机理。
笔者考虑砌体材料在受压破坏过程中的本构关系,分析偏心受压截面的弯矩和轴力关系,从而得出拱桥截面偏心距在拱桥破坏过程中的限制条件,然后通过非线性优化方法得出了石拱桥的极限承载力。并在此基础上讨论了砌体抗压强度对拱桥的极限承载力的影响。
1 砌体偏心受压截面分析
图1为砌体的典型受压应力-应变关系。图1中:ε0为砌体峰值应力对应的应变,根据试验和研究结论,砌体等准脆性材料内部存在很多微裂缝,在加载过程中,其力学性能主要由其内部微裂纹的损伤演化控制,从而体现出非线性的特征。可以考虑将砌体受压破坏的应力应变关系上升段用二次抛物线表示[9]:
(1)
式中:σ为应力;σmax为最大应力;ε为应变。

图1 砌体受压应力-应变关系Fig.1 Relationship of masonry compression stress-strain
在分析砌体偏心受压极限承载力时,假设截面变形符合平截面假定,即砌体内应变沿截面高度呈线性分布;并假设全截面受压时,砌体不会被压坏。(部分截面受压时才可能被压坏)。当截面偏心受压时,正截面远离偏心荷载的一侧由受压变为受拉而退出工作(假定砌体材料不承受拉应力),截面出现横向裂缝,压应变呈直线分布,如图2。

图2 砌体偏心受压示意Fig.2 Eccentrically loaded masonry
随着裂缝深度的不断增加,截面受压面积不断减小,当靠近偏心荷载的截面边缘达到最大应变ε0时,截面进入极限状态。设截面受压区高度为Y,以截面中性轴为坐标原点,由平截面假定:
(2)
因忽略砌体材料的抗拉强度,并利用截面平衡条件,可以得到轴力N和对O点的弯矩M:
(3)
式中:b为主拱圈宽度。
联立式(1)~式(3),可求得极限状态下偏心受压砌体截面的轴力和弯矩分别为:
(4)
(5)
关于截面中心的弯矩为:
(6)
式中:h为主拱圈厚度。
将M用N表示,得
(7)
由式(4)、式(6)、式(7)可以得到中心弯矩Mc和轴力N的关系为:
(8)
因此当砌体偏心受压到达极限承载能力时,截面偏心距与轴力的关系为:
(9)
可以看出,当截面受力达到极限状态时,截面的偏心距和截面轴力大小直接相关,轴力越大,偏心距越小;反之亦然。
将式(4)带入式(9),可以得出截面偏心距和受压区高度的关系为:
(10)
截面极限状态下偏心距与受压区高度关系如图3。由图3可看出,式(10)的计算值和已有砌体偏心受压时的实测受压区高度吻合得很好,这说明该模型较好地反映了砌体偏心受压的特征。
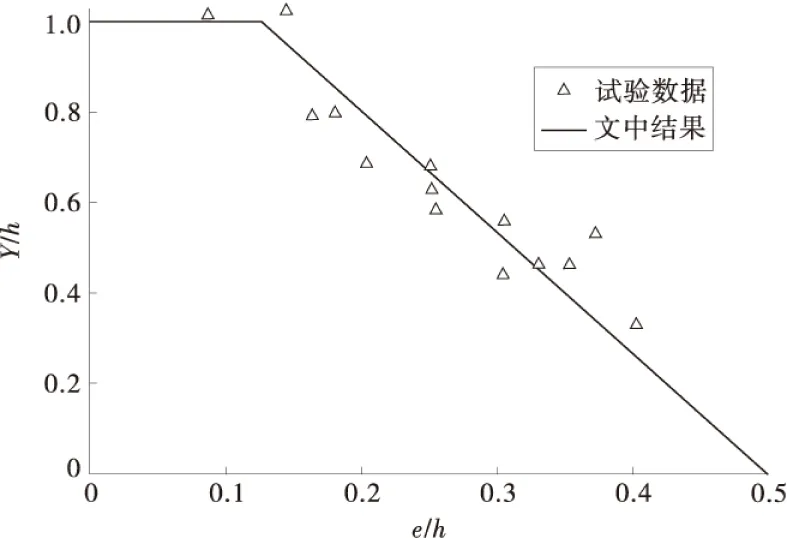
图3 截面极限状态下偏心距与受压区高度关系Fig.3 Relationship of eccentricity and effective height under the limited state of cross-section
2 石拱桥极限承载力研究
机构法是一种极限状态塑性分析法。分析拱桥承载力时,假定拱的破坏形态是4或5铰机构(对称加载)。机构法的思想是认为拱桥在承受外力荷载下,在不超过单个截面的承载能力时,由于拱桥是超静定结构,拱桥可以调节自身各截面内力使结构达到其最大承载能力。取左端拱脚反力的三元素为参数,主拱圈各个截面的平衡方程则可以写为:
Vn=∑(Pi+Wi)cosφn-V0cos(φ0-φn)-
H0sin(φ0-φn)
(11)
Hn=H0cos(φ0-φn)-∑(Pi+Wi)sinφn-
V0sin(φ0-φn)
(12)
Mn=-An-KBn+M0-H0(yncosφ0-xnsinφ0)+
V0(xncosφ0+ynsinφ0)
(13)
式中:An=∑Wi(Xn-Xwi)为恒载项;Bn=∑Pi(Xn-Xpi)为活载项;K为荷载系数;φ0和φn分别为拱角截面和拱桥计算截面与竖直方向的夹角,如图4。

图4 拱桥截面计算图示Fig.4 Calculation schematic of masonry arch section
由于拱桥材料本身有着一定的承载能力,截面极限状态时的轴力和弯矩应满足式(8)。拱桥承受荷载直至破坏的过程中,各个截面可以自动调整轴力和弯矩的关系使其承载能力最大。但无论如何调整,都不能超过拱桥材料自身的承载能力。由图1可以看出,应力随着应变的增加而增加,当受压截面处于极限状态时,一定轴力所能带来的弯矩是最大的。即石拱桥截面在受压直至破坏的过程中,其轴力和弯矩关系至多只能达到式(8)的状态,因此对于石拱桥的所有截面而言:
(14)
以往的分析认为,截面承载面积不会无限接近于0,压力线不能到达拱圈边界,即截面的偏心距应该小于h/2;通过式(14)可以看出,考虑砌体强度因素之后,偏心距的变化范围变得更小。
由上述分析可知,石拱桥的极限承载能力计算可以转化为一个非线性优化问题;该问题以拱脚支反力(轴力、剪力和弯矩)为设计变量,以式(11)~式(14)为优化限制条件,以活载系数K的最大值为优化目标函数。该问题可以通过非线性优化软件Lingo实现。
3 计算结果及讨论
3.1 极限位置推力线计算结果
考虑一个简单算例,拱桥拱轴线为圆弧,跨径60 m,矢跨比1/6,主拱圈厚度1.2 m,桥面宽10 m。砌体密度2 000 kg/m3,活载F为间距为2 m的集中力,均为100 kN,砌体的抗压强度为5 MPa。可以利用文中分析方法求出活载F沿主拱圈移动时拱桥的极限承载力。
利用优化方法可以求出各个工况下的最大荷载系数K及对应各个截面的内力,进而可以求出在石拱桥破坏时各个截面的偏心距。图5表示当活载分别作用于1/8,1/4,3/8主拱圈和拱顶时,各个截面的偏心距大小。
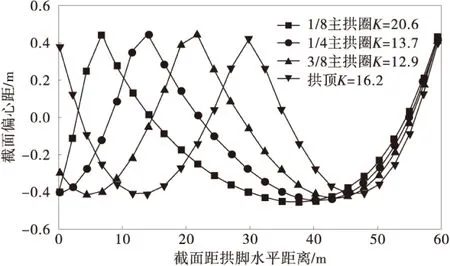
图5 砌体破坏偏心距Fig.5 Eccentricity of masonry failure




图6 石拱桥四铰或五铰示意破坏Fig.6 Failure of masonry arch sections (four or five hinges)
通过以上计算可以得出以下结论:
1)在拱桥承受外荷载直至破坏的过程中,拱桥的某些截面开裂,受力面积减小;并且这些截面发生受压塑性变形,在这些截面形成塑性“铰”,当铰的数目超过3个时,拱桥形成机构从而破坏。拱桥的破坏可以看成四铰或五铰破坏(对称加载)。
2)考虑砌体材料承载能力后,在达到石拱桥极限状态时,60 m石拱桥的偏心距只有主拱圈高度的4/11(如图6),与传统机构法的结论1/2或者4/9主拱圈高度相差较大。因此对于大跨径石拱桥,如果采用传统机构法的结论来判断石拱桥某截面是否形成“铰”,会过高的估计其变形和承载能力。
3)塑性铰出现的位置并不是仅仅是1/4主拱圈、拱顶和拱脚,而是和荷载的作用位置有关。
3.2 砌体抗压强度影响
为分析讨论砌体抗压强度对石拱桥极限承载能力的影响,笔者计算了不同活载作用位置下拱桥的极限承载能力,然后与传统机构法(砌体抗压强度为无穷大)的计算结果进行比较,如图7。
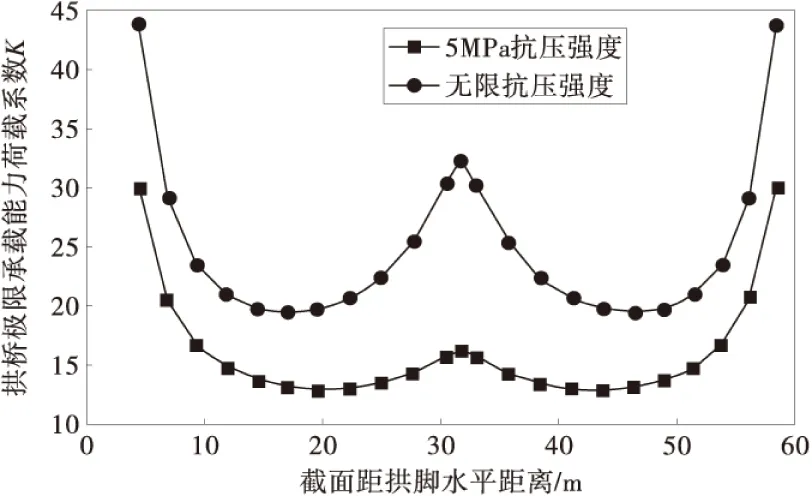
图7 压力作用位置和拱桥极限承载力关系Fig.7 Relationship of load position and masonry arch limit strength
当考虑砌体材料有限承载能力后,石拱桥的极限承载能力比传统方法有所降低,因此传统机构法会过高的估计石拱桥的承载能力。
同时从图8中可看出,在考虑砌体材料承载能力后,理论计算结果表明,最不利荷载位置并不是传统方法认为的1/4主拱圈处,而是更靠近拱顶截面。
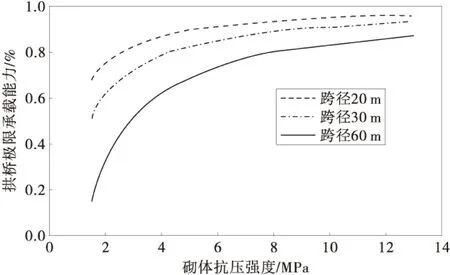
图8 砌体抗压强度和拱桥极限承载力关系Fig.8 Relationship of material strength and masonry arch limit strength
为分析计算砌体抗压强度对不同跨径石拱桥极限承载力的影响,计算矢跨比为1/6,跨径分别为60,30,20 m的石拱桥,其主拱圈厚度分别为1.2,0.6,0.3 m,宽度均为10 m,活载均作用于1/4跨处,距离为2 m的100 kN集中力。
从图8可以看出,砌体抗压强度越小,石拱桥的承载能力越低。这是因为对不同抗压强度的砌体,由于截面极限状态下轴力和弯矩关系不同,因此截面偏心距的限制条件有所差别;砌体强度越小,极限状态下承受同等轴力的截面受压区高度就越大,偏心距就越小,石拱桥极限承载能力就越低。并且对于跨径较大的石拱桥而言,由于其自重产生的恒载较大,自身轴力也较大,由式(8)和式(14)可知,拱桥截面偏心距的变化范围较小,这时砌体抗压强度的影响更大。
4 结 论
考虑砌体受压的本构关系,分析了砌体偏心受压截面内力之间的联系,得出了砌石拱桥截面偏心距与受压区高度的关系以及偏心距的限制条件。在此基础上,利用非线性优化的机构分析法计算了石拱桥的极限承载力;并讨论了砌体抗压强度对石拱桥极限承载力的影响。利用笔者的分析方法,可以得出以下结论:
1)与以往文献提及的方法相比,笔者考虑了砌体材料的本构关系,更能反映石拱桥的受力特征及破坏机理。
2)砌体材料的抗压强度对其承载能力有一定的影响,若材料抗压强度较低,石拱桥的承载能力会显著降低;大跨径拱桥程度更加明显。对于长期服役的石拱桥而言,砌体材料性能的劣化会加速拱桥结构性能的破坏。
3)需要指出的是,笔者在研究中仅考虑了主拱圈的承载能力,而未计算拱上结构和填土对石拱桥承载力的影响,准确地分析材料对拱桥结构的影响规律还需进一步研究。
[1] 周建庭,黎小刚,屈建强,等.复合主拱圈加固石拱桥力学性态分析[J].重庆交通大学学报:自然科学版,2010,29(6):849-851. Zhou Jianting,Li Xiaogang,Qu Jianqiang,et al.Mechanical behavior analysis on stone arch bridge strengthened by composite main arch circle method[J].Journal of Chongqing Jiaotong University:Natural Science,2010,29(6):849-851.
[2] 贺国银,周建庭,刘璐.在役石拱桥实用安全性鉴定技术[J].重庆交通大学学报:自然科学版,2009,28(3):525-527. He Guoyin,Zhou Jianting,Liu Lu.Practical security identification technology of stone Arch bridge in service[J].Journal of Chongqing Jiaotong University:Natural Science,2009,28(3):525-527.
[3] Heyman J.The Masonry Arch[M].New York:Ellis Horwood,Ltd.,1982.
[4] 钱令希.赵州桥的承载能力分析[J].土木工程学报,1987,20(4):39-48. Qia Lingxi.The carrying capacity of Zhaozhou stone arch bridge[J].China Civil Engineering Journal,1978,20(4):39-48.
[5] 陈荣刚,郑振飞.石拱桥极限承载能力分析[J] .福州大学学报:自然科学版,2002,30(1):92-97. Chen Ronggang,Zheng Zhenfei.Ultimate bearing capacity analysis of stone arch bridges[J].Journal of Fuzhou University:Natural Science,2002,30(1):92-97.
[6] Boothby T E,Domalik D E,Dalal V A.Service load response of masonry arch bridges[J].Journal of Structural Engineering,1998,124(1):17-23.
[7] Smith F W,Harvey W J,Vardy A E.Three-hinge analysis of masonry arches[J].Structural Engineering,1990,68(11):203-213.
[8] Orduna A,Lourenco P B.Cap model for limit analysis and strengthening of masonry structures[J].Journal of Structural Engineering,2003,129(10):1367-1375.
[9] Powell B,Hodgkinson H R.Determination of Stress/Strain Relationship of Brickwork[M].Stoke,England:British Ceramic Research Association,1976.
Limit Strength of Masonry Arch Bridge Considering the Constitution of Masonry
Zheng Dan, Huang Caizheng
(School of River & Ocean Engineering, Chongqing Jiaotong University, Chongqing 400074, China)
The relationship of moment and axial load of eccentrically loaded masonry section were analyzed, considering constitution of masonry material under compression till failure. The limit strength of masonry arch was achieved by nonlinear optimization mechanism analysis. The influence of masonry strength on limit strength of masonry arch was also discussed. The results show that when the compressive strength of masonry materials is low, bridge bearing capacity on the material strength is relatively sensitive, and with the bridge span increasing, the sensitivity is further increased.
bridge engineering; masonry arch bridge; masonry; eccentrically compress; nonlinear optimization
10.3969/j.issn.1674-0696.2015.05.03
2014-09-28;
2014-11-23
交通运输部应用基础项目(2012319814210);重庆市科委项目(cstc2012jjA1026)
郑 丹(1979—),男,重庆人,教授,博士,主要从事混凝土材料性能方面的研究。E-mail:zhengdan@cquc.edu.cn。
U441+.5;TU365
A
1674-0696(2015)05-014-04

