基于灰色神经网络的港口集装箱吞吐量预测模型研究

张树奎，肖英杰，鲁子爱

(1．江苏海事职业技术学院 航海技术系，江苏 南京 211170；2．上海海事大学 商船学院，上海 201306； 3．河海大学 港口、海岸与近海工程学院，江苏 南京 210098)



基于灰色神经网络的港口集装箱吞吐量预测模型研究

张树奎1，2，肖英杰2，鲁子爱3

(1．江苏海事职业技术学院 航海技术系，江苏 南京 211170；2．上海海事大学 商船学院，上海 201306； 3．河海大学 港口、海岸与近海工程学院，江苏 南京 210098)

为降低港口集装箱吞吐量的预测误差，提高预测精度，在分析传统的灰色预测模型和BP神经网络预测模型的优缺点的基础上，构建了灰色神经网络港口集装箱吞吐量预测模型，该模型充分发挥了灰色模型所需初始数据少和BP神经网络非线性拟合能力强的特点。以实际数值作为初始数据，各种灰色模型的预测值为神经网络的输入值，神经网络的输出值为组合预测结果。通过实例分析，结果表明：灰色神经网络预测模型提高了预测精度，预测结果比较理想，优于单一预测模型，因此，该模型用于港口集装箱吞吐量预测是可行的、有效的。

交通运输工程；吞吐量；预测；灰色模型；灰色神经网络

当前，港口之间的竞争日益表现为以集装箱吞吐量为核心指标的综合实力的竞争。港口集装箱吞吐量的科学预测是港口主管部门科学规划和决策的理论基础，它对港口建设，基础设施投资规模，港口发展方向，经营策略以及港口发展战略等都具有现实的指导意义，是不可或缺的重要依据。

传统的港口集装箱吞吐量的预测方法主要有线性回归分析法[1]，指数平滑法，灰色模型法等；目前，新的预测方法主要有灰色多元回归模型法[2]，组合模型法[3]等。然而，港口集装箱吞吐量与港口腹地、经济发展状况、港口自然条件、交通条件以及国家经济政策和周边港口发展等密切相关，受到多种因素的影响，且各因素的作用机制很难用准确的数学语言来描述，具有明显的非线性特征；因此，对其的预测是一个复杂的系统过程。上述每个单一的预测方法都有一定的片面性，而部分组合预测方法又较少考虑集装箱吞吐量预测具有非线性的特点。所以，两种方法预测误差都较大，难以满足预测要求。

笔者根据灰色系统理论预测模型所需数据量较少、计算方法简单、不需要太多的关联因素以及可用于短、中、长期预测的特点和神经网络所具有的自学习、非线性映射以及并行分布处理的能力[4]，将两者结合，发挥两种方法的各自优势，避免其局限性，从而达到提高港口集装箱吞吐量预测精度的目的。

1 预测模型的构建

1.1 建模原理

灰色预测理论是根据部分信息已知，部分信息未知的历史数据，建立一个能够表达信息发展的GM(Gray Model)模型，从而揭示信息未来发展规律，做出预测[5]。目前，灰色预测方法在各领域应用非常广泛[6-7]，但是灰色预测模型缺乏自学习、自组织和自适应能力，对信息处理能力较差，难以控制预测误差。

人工神经网络是一种通过模仿动物神经网络行为特征，对信息进行分布并行处理的算法数学模型[8]。人工神经网络预测模型具有很强的非线性映射能力，能够对输出误差进行反馈校正，在一定条件下能够任意逼近模型，预测精度非常高，其中以BP(Back Propagation)网络应用最为广泛和成功。

笔者将灰色预测理论和神经网络相结合，构建灰色神经网络(Gray Neural Network,GNN)预测模型对港口集装箱吞吐量进行预测，通过两者结合，体现优势互补，提高预测精度。

1.2 模型构建

笔者选择最常用、最简单的GM(1，1)灰色模型[9-10]和BP神经网络相结合，建模步骤如下。

1)设已知的历史港口集装箱吞吐量x(0)的初始数据序列为：

(1)

式中：n为序列长度。

2)对历史数据进行一次累加生成(AGO)处理，目的是为了弱化数据的随机性和波动性：

新生成的数据序列记为：

(2)

3)建立一阶线性微分方程：

(3)

式中：α，μ为待辨识参数，分别表示发展系数和灰色作用量。

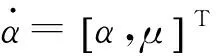
利用最小二乘法求解可得：

(4)

5)将得到的参数向量带入式(1)，求解微分方程得到时间响应方程：

(5)

离散响应方程为：

(6)

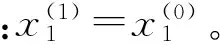
(7)

7)对不同时间序列长度的初始数据运用等维灰数递补法，得到不同的港口集装箱吞吐量GM模型：GM1，GM2，…，GMk。

8)确定神经网络结构：神经网络的结构一般采用3层BP网，即输入层、隐含层和输出层，其中输入为各种GM的预测结果，对预测结果数据进行归一化处理后，结果可视为输入神经元，其个数为3；输出为灰色神经网络组合预测结果，可视为输出神经元，个数为1；隐含层神经元个数与输入、输出神经元的个数有关，可用试验的方法确定。笔者参考以下经验公式设计，并根据训练结果，最终确定隐含层节点数：

9)采用误差反向传播学习方法训练神经网络，直到误差达到要求精度为止。此时的神经网络才是最好的神经网络，其结构如图1。当输入端为港口集装箱吞吐量的各种GM预测值时，则输出端为灰色神经网络组合的预测值。

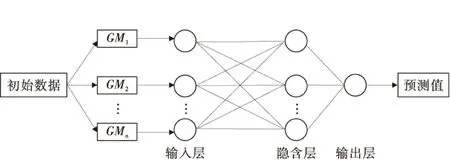
图1 灰色神经网络模型结构Fig.1 Structure of Grey neural network model

2 实例及数据分析

采用南京港1990年到2013年共24年的港口集装箱吞吐量数据作为实验数据来验证模型；设计灰色预测模型GM1，GM2，GM3，BP神经网络模型以及GNN组合模型；应用前15年的数据作为初始数据，预测后9年内的港口集装箱吞吐量。

GM1，GM2，GM3建模所用的时间序列长度分别为10，8，6，为确保预测精度，采用等维递推滚动预测方法[11-12]，即每次预测一个港口集装箱吞吐量后，添加一个新的数据，去掉最早的一个数据，以保持数据序列等维，重新建模预测下一个值，这样依次递补进行预测。

BP神经网络模型采用3×6×1结构，输入层与隐含层的传递函数为Sigmoid型，取前15年的实际港口集装箱吞吐量值作为样本训练网络，并对样本进行归一化处理，其值域为[0,1]，将前3个实际吞吐量值作为输入，第4个实际吞吐量值作为输出，设计最大学习次数为18 000次，学习速度为0.002，取学习目标误差平方和为0.1。

采用GNN组合模型进行预测时，GM1，GM2，GM3的预测值作为输入值。因此，输入神经元个数为3，输出为1。设计最大学习次数为18 000次，学习速度为0.002，取学习目标误差平方和为0.1。设计训练步数为3 000时，训练误差达到1×9-3，满足预计设计学习精度要求，所以取GNN神经网络结构为3×9×1。分别对GM1，GM2，GM3，BP，GNN模型进行MATLAB仿真，采用后9年的实际集装箱吞吐量数据预测集装箱吞吐量，预测结果见表1。

表1 GM(1,1)、BP神经网络和GNN预测值

对表1中的各模型的相关预测数据与实际数据建立坐标图进行比较，其中横轴表示时间，纵轴表示每年的集装箱吞吐量。坐标如图2，从图2可以看出，GNN模型预测曲线更接近实际测量数据曲线，说明GNN模型优于其它各单一预测模型。

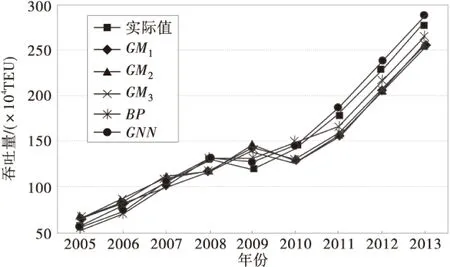
图2 各种模型的预测结果比较Fig.2 Comparison of predicted results with different models

令港口集装箱吞吐量的预测值为dpre，实际值为dmea；dpre与dmea的关联系数为C，效果系数为E，一致性指标为A[13]，则有:

(8)

(9)

(10)

关联系数和效果系数越接近1，说明预测值越接近实际值，一致性指标的值域为[0,1]，值越接近1，说明预测值与实际值的变化曲线越趋于一致，拟合度就越好。采用表示各单一模型和GNN模型的拟合度，建立表2。从表2中可以看出：GNN模型的拟合度值均大于对应的单一模型的值，说明GNN模型不仅适用于港口集装箱吞吐量的预测，而且好于上述其它单一预测模型。

表2 GM(1,1)、BP神经网络和GNN拟合度检验

对表1中各模型的相关预测数据与实际数据取平均相对误差(表3)作为评价指标，对各预测模型进行评价。由表3可以看出：与各单一预测模型比较，GNN预测模型的平均误差均小于其它单一预测模型对应的值；最大误差也均小于其它单一预测模型的最大误差；特别是在实际数据变化幅度较大的2009年和2011年，GNN预测模型的平均误差值与其它单一预测模型的平均误差值相比较要小得多，预测效果明显。

表3 各种模型预测值相对误差比较

Table 3 Comparison of relative deviation of predicted results with different models

年份实际值单一模型/%GM1GM2GM3BPGNN预测值/%200558.7710.8614.549.378.594.46200678.939.927.6211.0110.915.76

(续表3)

年份实际值单一模型/%GM1GM2GM3BPGNN预测值/%2007104.293.856.685.212.661.842008128.039.979.048.042.581.872009120.0314.2121.7818.909.516.262010141.5610.619.148.656.082.282011180.0715.9813.2812.207.703.862012229.089.3710.789.124.934.022013279.767.989.948.765.092.88

对后9年的预测数据取平均相对误差，均方根误差，最大相对误差以及最小相对误差(表4)作为评价指标，讨论各预测模型。从表4中可以看出，GNN预测结果明显优于单一GM预测和BP神经网络预测方法，表现为GNN的4个评价指标值均小于对应的单一预测模型的评价指标值。GNN预测更接近实际测量值。

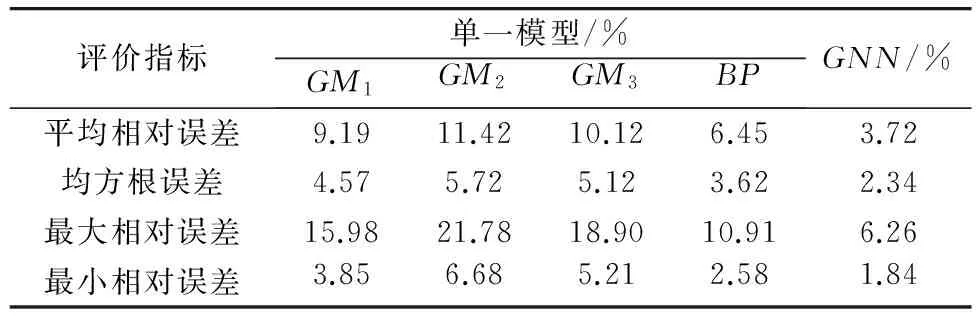
表4 各种预测结果相对误差比较

3 结 论

笔者通过采用5个预测模型对南京港口集装箱吞吐量进行预测，并对其相对误差进行比较，得到如下结论：

1)与其它4个单一模型比较，GNN模型的预测结果更接近实际值，预测精度更高。

2)GNN模型充分利用了GM模型所需初始数据少、计算方法简单和BP模型非线性强的优点，提高了预测精度。

3)GNN预测模型不仅适用于港口集装箱吞吐量预测，还可用于其它领域的预测，应用范围广泛。

[1] 陈秀瑛,古浩.灰色线性回归模型在港口吞吐量预测中的应用[J].水运工程,2010(5):89-92. Chen Xiuying,Gu Hao.Application of grey linear regression model for forecast of port throughput [J].Port & Waterway Engineering,2010(5):89-92.

[2] 林强,陈一梅.灰色多元回归模型在港口吞吐量预测中的应用[J].水运工程,2008(7):77-80. Lin Qiang,Chen Yimei.Grey multiple regression model applied for port throughput forecasting [J].Port & Waterway Engineering,2008(7):77-80.

[3] 刘志杰,季令,叶玉玲,等.基于径向基神经网络的集装箱吞吐量组合预测[J].同济大学学报:自然科学版,2007,35(6):739-744. Liu Zhijie,Ji Ling,Ye Yuling,et al.Combined forecast method of port container throughput based on RBF neural network [J].Journal of Tongji University:Natural Science,2007,35(6):739-744.

[4] 于莉,马晓平.灰色理论在造船工序作业计划预测中的应用研究[J].江苏科技大学学报:自然科学版,2007,21(2):17-19. Yu Li,Ma Xiaoping.Application research on grey-theory in forecast of shipbuilding process operation plan [J].Journal of Jiangsu University of Science and Technology:Natural Science Edition,2007,21(2):17-19.

[5] 邱洪波,杨斌,黄勇.基于灰色理论的城市核心区道路交通安全分析[J].重庆交通大学学报:自然科学版,2013,32(6):1228-1231. Qiu Hongbo,Yang Bin,Huang Yong.Road traffic safety analysis at the core area of city based on the grey system theory [J].Journal of Chongqing Jiaotong University:Natural Science,2013,32(6):1228-1231.

[6] 傅立.灰色系统理论及其应用[M].北京:科学技术文献出版社,1992:18-24. Fu Li.Grey System Theory and Its Applications [M].Beijing:Science and Technology Press,1992:18-24.

[7] 张树奎,鲁子爱.港口环境资源的生态性评价方法研究[J].江苏科技大学学报:自然科学版,2010,24(2):179-183. Zhang Shukui,Lu Zi’ai.Ecology evaluation method of port environment resource [J].Journal of Jiangsu University of Science and Technology:Natural Science Edition,2010,24(2):179-183.

[8] 王伟.人工神经网络原理[M].北京:北京航空航天大学出版社,1995:46-51. Wang Wei.Artificial Neural Network Theory [M].Beijing:Beijing University of Aeronautics and Astronautics Press,1995:46-51.

[9] 吴志周,范宇杰,马万经.基于灰色神经网络的点速度预测模型[J].西南交通大学学报,2012,47(2):285-290. Wu Zhizhou,Fan Yujie,Ma Wanjing.Spot speed prediction model based on grey neural network [J].Journal of southwest Jiaotong University,2012,47(2):285-290.

[10] 范嫦娥,李德华.基于自组织特征映射神经网络的路面使用性能评价方法[J].重庆交通大学学报:自然科学版,2013,32(1):80-83. Fan Chang’e,Li Dehua.Pavement performance evaluation based on SOM neural network [J].Journal of Chongqing Jiaotong University:Natural Science,2013,32(1):80-83.

[11] 周鹏飞,温胜强,康海贵.基于马尔可夫链与神经网络组合的路面使用性能预测[J].重庆交通大学学报:自然科学版,2012,31(5):997-1001. Zhou Pengfei,Wen Shengqiang,Kang Haigui.Pavement performance combining forecasting based on BP neural network and Markov model [J].Journal of Chongqing Jiaotong University:Natural Science,2012,31(5):997-1001.

[12] 陈淑燕,王炜.交通量的灰色神经网络预测方法[J].东南大学学报:自然科学版,2004,34(4):541-544. Chen Shuyan,Wang Wei.Grey neural network forecasting for traffic flow [J].Journal of Southeast University:Natural Science Edition,2004,34(4):541-544.

[13] Legates D R,Mccabe G J.Evaluating the use of goodness of fit measures in hydropic and hydro-climatic model validation [J].Water Resources,1999,35(1):233-241.

Prediction Model of Port Container Throughput Based on Grey Neural Network

Zhang Shukui1, 2, Xiao Yingjie2, Lu Zi’ai3

(1. Department of Navigation, Jiangsu Maritime Institute, Nanjing 211170, Jiangsu, China; 2. College of Merchant, Shanghai Maritime University, Shanghai 201306, China; 3. College of Harbor, Coastal & Offshore, Hohai University, Nanjing 210098, Jiangsu, China)

In order to reduce prediction error of port container throughput and improve its prediction accuracy, a Grey neural network model of port container throughput was constructed after analyzing the advantages and disadvantages of the conventional Grey model and BP neural network model. The new model made full use of the characteristic of low data demand of Grey model and strong nonlinear fitting ability of BP neural network. The actually measured values were used as the initial data, and various prediction values of Grey model were used as input data of neural network and final output data of neural network was used as combination prediction result. A case study shows that the Grey neural network model can offer improved prediction accuracy and ideal prediction results, which is better than single forecasting model. Therefore, it is feasible and effective to predict port container throughput by Grey neural network model.

transportation engineering; throughput; prediction; grey model; grey neural network

10.3969/j.issn.1674-0696.2015.05.27

2014-04-24；

2014-07-08

2013年度江苏省教育教学研究课题项目(ZYB210)；2013年交通运输职业教育科研立项项目(2013A03)

张树奎(1973—)，男，安徽阜阳人，副教授，博士，主要从事港口、海岸与近海工程及航海技术方面的研究。E-mail: zhangshkfy@163.com。

U 695.2

A

1674-0696(2015)05-135-04