谁买了棒棒糖

林革

杰克、汤姆、乔治和丹尼揣着一些零花钱走进了一家糖果店。售货员热情地向他们介绍店里刚刚进的四种新糖果，一种是0.6美元一盒的果仁夹心糖，一种是0.5美元一盒的棒棒糖，一种是0.4美元一盒的甘草糖，一种是0.3美元一盒的奶糖。四人挑选了一下，最终每人各挑了一种心仪的糖果（四人所挑的糖果正好各不相同），其中杰克要了2盒选中的糖，汤姆则要了8盒，乔治和丹尼分别拿了5盒和4盒。

到收银台结账时，四个小伙子拿出了他们全部的零花钱：一些5美元和1美元的钞票，还有一个50美分和一个10美分的硬币。巧的是，他们口袋里的这些钱，不多不少刚好够付账，买卖双方都很开心。不过，你知道是谁买了棒棒糖吗？

要解决这个问题，必须要排除纷繁复杂的数量关系干扰，寻找突破口，从而简化结构，降低难度，构造解题桥梁。

我们先进行第一步推理。首先必须明确的是1美元=100美分的换算。根据付账零花钱的描述可知，所有糖果的费用如果统一用“美分”作单位的话，那么金额总数的最后两位肯定是60。因为1美元和5美元的钞票无论有多少张，换成美分相加，也就相当于整百数相加，加起来尾数只会是00，而不是整百数的只有50分和10分，所以金额总数用美分表示时最后两位肯定是60。

接下来的第二步推理，我们用X，Y，Z，T分别表示杰克、汤姆、乔治和丹尼所买的四种糖果的单价，显然X，Y，Z，T分别对应30，40，50，60中的一个，但具体对应情形还不清楚。不过从第一步推理可知，四人买的糖果的总金额可列式为2X+8Y+5Z+4T，且这个式子的结果最后两位数是60。

我们对第二步推理得到的结论进行简化处理——将式子两边同时缩小10倍。即原先X，Y，Z，T分别对应30，40，50，60中的一个数，缩小10倍后，分别对应3，4，5，6这四个数中的一个，用x，y，z，t表示。则有：2x+8y+5z+4t的结果的最后一位数是6。此时我们仍然无法知道x，y，z，t分别对应的是3，4，5，6中的哪一个数。

但根据以上推论可知，2x+8y+5z+4t的结果是偶数，而其中2x，8y，4t肯定是偶数，所以5z也必定是偶数，则z必为偶数，即z=4或6，那么，5z的最后一位肯定是0，由此可知2x+8y+4t的最后一位是6，进而推知x+4y+2t的最后一位是3或8。

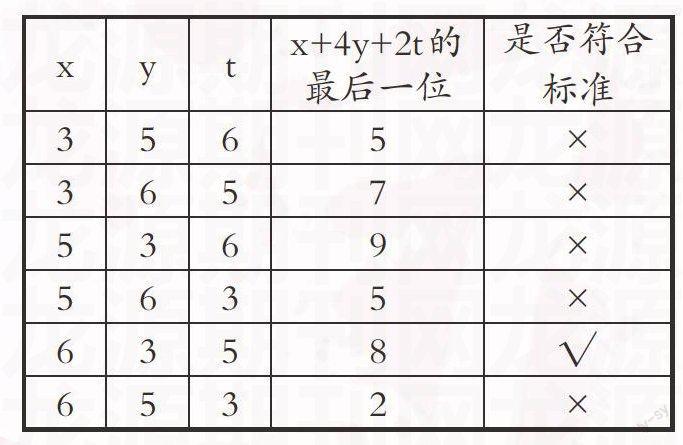
当z =4时，x，y，t对应3、5、6中的一个，可能的情形有以下6种（见下表）：

虽然上表中出现了符合“当z=4或6，x+4y+2t的最后一位是3或8”这个推论的情形，但我们还需要讨论当z =6时，x，y，t对应3，4，5中的一个的情形，列表可知有以下6种情形（见下表）：

从上表中不难看出，当z =6时，没有出现符合标准的答案，故只有z =4，x=6，y=3，t=5这种对应情况符合题意。也就是说，拿了2盒糖果的杰克买的是0.6美元的果仁夹心糖，拿了8盒糖果的汤姆买的是0.3美元的奶糖，拿了5盒糖果的乔治买的是0.4美元的甘草糖，而拿了4盒糖果的丹尼买的是0.5美元的棒棒糖。

你答对了吗？