基于田口方法的汽车悬架稳健性优化

张 瑛，吴光强，2

（1.同济大学汽车学院，上海 201804；2.东京大学生产技术研究所，东京 153-8505）

基于田口方法的汽车悬架稳健性优化

张 瑛1，吴光强1，2

（1.同济大学汽车学院，上海 201804；2.东京大学生产技术研究所，东京 153-8505）

0 引言

悬架的运动学特性直接影响到汽车的使用性能，在车轮上下跳动的过程中，悬架性能参数的变化特性对操纵稳定性、舒适性、转向轻便性和轮胎的使用寿命至关重要。由于各性能参数之间互相约束，悬架空间机构比较复杂，这给悬架的设计与优化带来很大困难。对此，许多学者进行了研究，有些通过空间机构运动学、多体动力学等方法对麦弗逊悬架进行了运动学分析［1-2］；有些采用遗传算法、层次分析法等方法对悬架进行了多目标优化［36］，但在优化中都没有考虑到稳健性；有些虽考虑了随机因素的影响对悬架进行了稳健性优化，但是没有考虑到制造、安装的误差因素［78］等。悬架部件在生产、制造及安装过程中必然存在一定的误差，这些误差可能会使悬架实际性能相对设计性能有很大偏差，因此，为了保证悬架性能稳定，在设计中考虑稳健性很有必要。

在此，考虑悬架安装位置误差的影响，采用经典的田口稳健性设计方法对麦弗逊悬架进行稳健性优化，保证一定范围内的误差不会对性能产生太大影响，并通过蒙特卡罗抽样法验证了优化结果。同时，通过建立悬架的数学模型来代替多体模型，避免了稳健性优化过程中由于需要考虑方差而带来的计算量过大的问题，大大提高了计算效率。

1 麦弗逊独立悬架运动学模型的建立

建立如图1所示的麦弗逊独立悬架运动学模型，通过几何关系得到悬架性能的评价指标。

图1 麦弗逊独立悬架简化模型

图1中，OB为下横臂，DE为减振器轴线，SP为横拉杆，F为车轮中心，E为滑柱与转向节交点，P为横拉杆与转向节交点，B为下横臂与转向节交点，DB为主销轴线，G为垂直于车轮平面的车轮轮轴与主销轴线交点。

1.1 悬架性能参数

1.1.1 前束角

汽车的前束角由轮轴GF的端点坐标值确定。规定车轮前束角向内为正，前束角为：

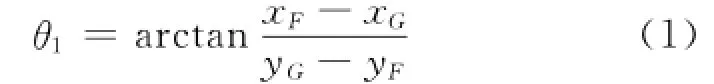
1.1.2 外倾角

车轮外倾角由轮轴GF端点坐标值确定。规定向外倾时为正，外倾角为：

1.1.3 主销后倾角

主销后倾角由主销轴线DB端点坐标确定。规定向后倾时为正，主销后倾角为：

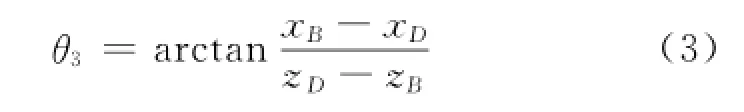
1.1.4 主销内倾角

主销内倾角由主销轴线DB端点坐标确定。规定内倾时为正，则主销内倾角为：

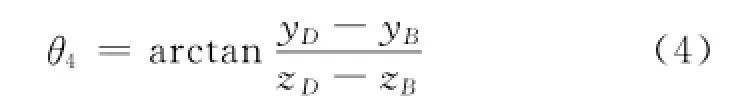
1.2 模型的试验验证

在试验台上进行了某车的悬架K＆C台架试验，将车身及方向盘锁死，通过施加制动力矩使车轮不能绕自身旋转轴转动，左右车轮在垂直加载缸的作用下同向跳动，每一时刻左右车轮垂直位移相同，得到平行轮跳试验中车轮前束角变化、外倾角变化等数据。同时根据上述分析在Matlab中进行编程，求得该车车轮上下跳动100 mm过程中，悬架性能参数的变化，将平行轮跳试验结果与计算结果进行对比。如图2所示。通过比较可以看出，在车轮上下跳动过程中，悬架K特性计算值与实验数据较吻合，证明了该模型的可用性。

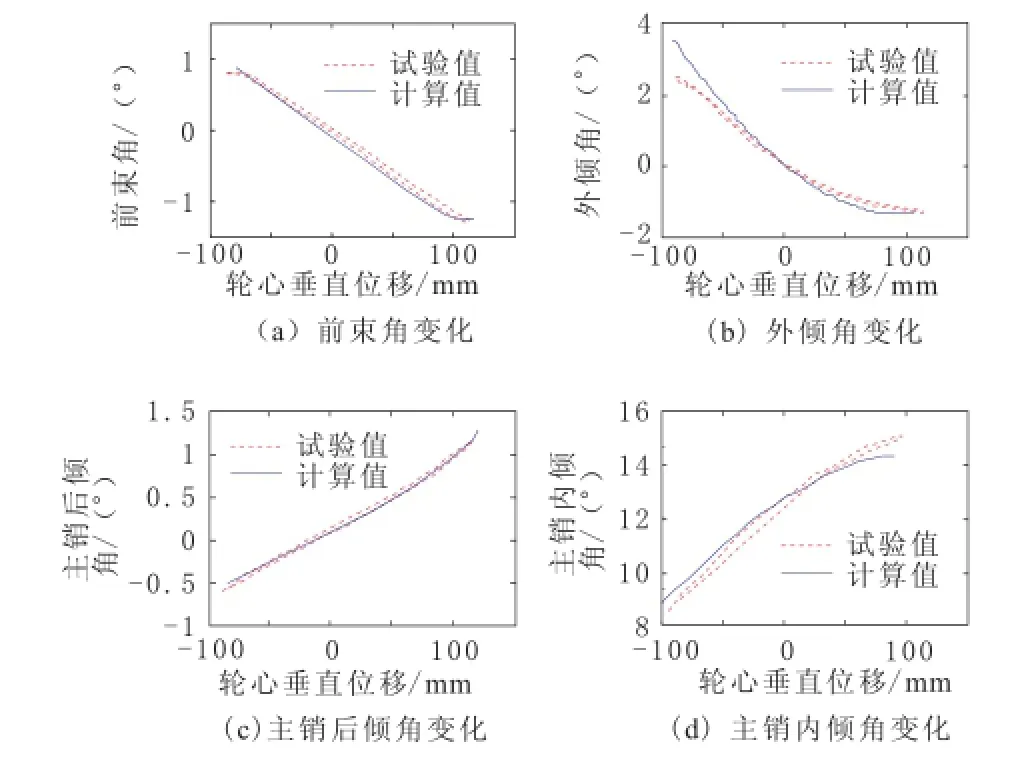
图2 悬架K特性试验与计算结果对比

2 悬架的多目标稳健性优化设计

2.1 田口稳健性设计理论

稳健性是指产品对各种干扰因素的抵抗能力，反映为产品质量特性的变异程度，变异小的产品稳健性就高，变异程度大的产品稳健性就低。任何一件产品都有一些影响其质量的因素，在产品设计阶段要考虑可控因素和不可控因素。田口将不可控因素称为噪声因素，利用质量损失函数和信噪比作为评价指标来衡量产品的稳健性［910］。

能够反映产品质量的指标被称为质量特性值，通常用质量特性值接近于目标值的程度来评定产品质量，质量特性值愈接近目标值，质量愈好，偏离目标值越远，质量越差。当产品特性值与目标值不相等时，就认为造成了质量损失，田口用平方损失函数来描述这种损失［11-12］。

设产品质量特性值为y，目标值为m，质量损失函数为：

由于y具有随机性，假定响应的测量值分别为y1，y2，…，yn，y服从正态分布y～N（μy，σ2y），期望均值μy尽量接近m，且σ2y越小越好。产品质量采用平均质量损失函数来衡量：

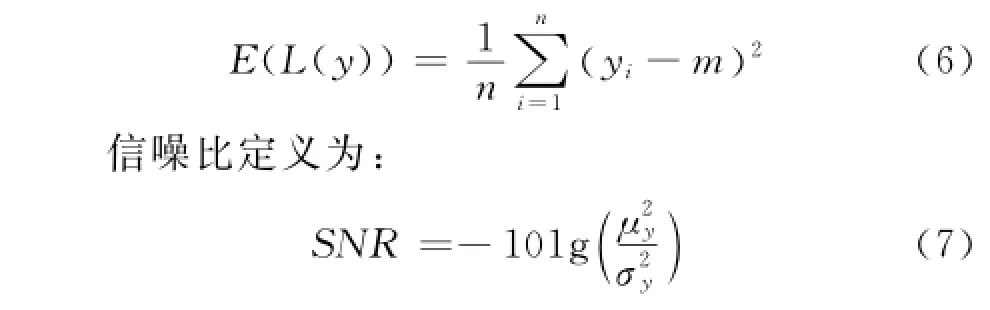
对于悬架跳动力学特性，其质量特征要求：不取负值，越小越好，目标值为零。这种质量特征称为望小特性，其质量损失函数为：

信噪比越大说明质量损失越小，产品质量越好。

2.2 悬架硬点灵敏度分析

硬点灵敏度分析在ADAMS／Insight中完成，由两水平DOE Screen（筛选法）方法找出对悬架特性影响显著的因素。利用左右车轮同时跳动工况分析悬架的运动学特性，以前束角、外倾角、主销内倾角和主销后倾角为响应目标。选择O、B、S、P、D、E、F、G 8个点共24个坐标进行分析，自变量取在原始硬点坐标基础上变化正负10%。根据分析结果选取8个坐标（如表1）作为优化控制参数。

表1 悬架硬点灵敏度分析%

2.3 优化因素选择

根据灵敏度分析，将选取的8个因素作为可控因素。即

每个因素选取3个水平，制定因素水平表如表2所示。

同时将悬架硬点误差作为噪声因素，即

Xi为第i个水平可控因素的取值（i＝1，2，3），ΔX为允许误差，根据本文优化设计要求，此处取为1 mm。

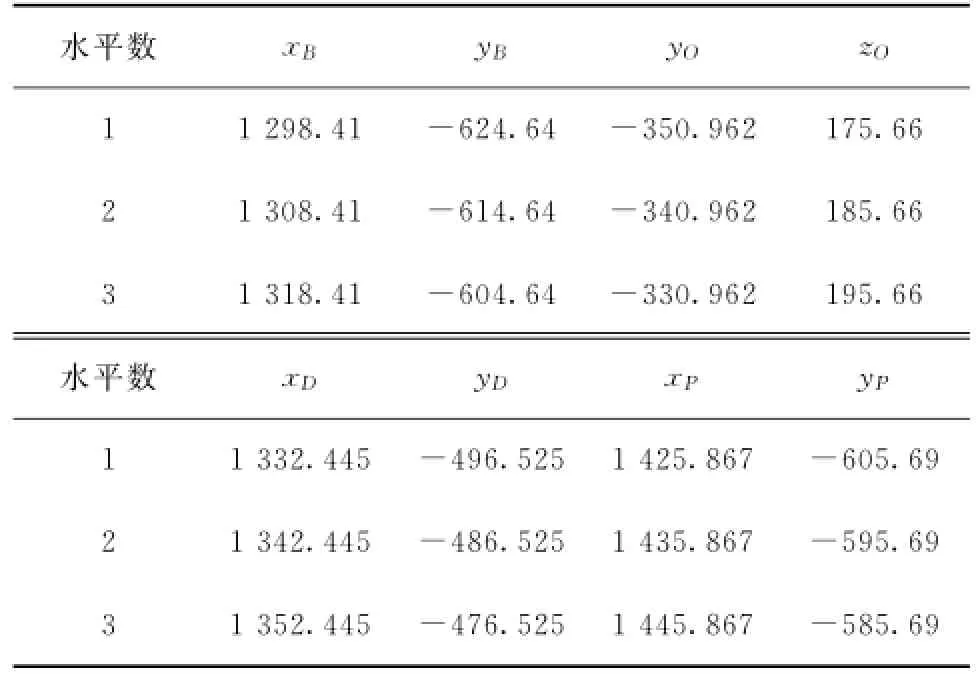
表2 可控因素水平表

2.4 目标函数

车轮上下跳动过程中，前束角、外倾角、主销后倾角以及主销内倾角的变化，对车辆直行稳定性以及稳态响应有重要影响，设计上希望车轮跳动过程中这些悬架性能参数能在较小的范围内变动。设车轮上下跳动距离h为－100 mm≤h≤100 mm，麦弗逊独立悬架跳动特性的稳健性优化目标表示如下所述。

a.车轮上下跳动过程时，前束角相对于平衡位置的变化量绝对值加权之和。

θ1（h）为跳动距离h时的前束角；θ1（0）为初始平衡位置的前束角；w（h）为位置加权系数。

b.车轮上下跳动过程中，外倾角相对平衡位置的变化量绝对值加权之和。

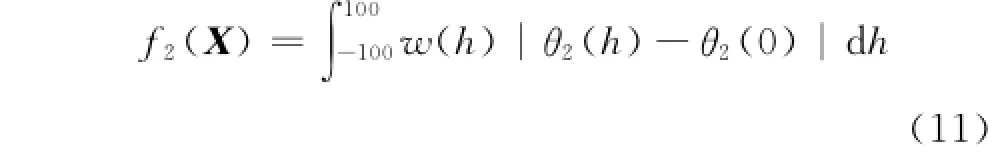
c.车轮上下跳动过程中，主销后倾角相对平衡位置的变化量绝对值加权之和。

d.车轮上下跳动过程中，主销内倾角相对平衡位置的变化量绝对值加权之和。

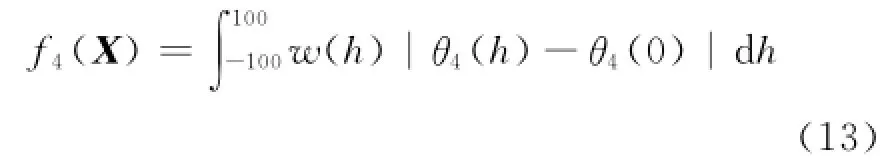
位置加权系数的选取，主要考虑车辆在设计工况附近工作的情况较多，因此，悬架在平衡位置附近的位置加权系数应该大，离平衡位置越远系数越小。按照此标准选取的位置加权函数［11］为：

由于上述4个目标相互冲突，无法使其同时达到最优，在此将各个目标函数加权然后求和［6］，得到目标函数为：

2.5 田口方法稳健性优化

田口方法稳健性优化的基本工具是正交实验设计，根据2.3节中可控因素和噪声因素的确定，按照正交实验设计方法，不考虑参数间的交互作用，可控因素用正交表L27、噪声因素用正交表L12组合成内外正交表，一共进行27×12＝324次实验。由于稳健性分析过程需要考察由不确定因素产生的方差，计算量比确定性优化将大大增加，采用多体模型导致计算时间过长，因此将前面建立的数学模型作为优化模型，通过Isight与Matlab联合仿真，进行悬架稳健性优化。得到优化函数均值主效应如图3所示，信噪比主效应如图4所示。

图3 响应均值主效应图

图4 信噪比主效应图

对图3和图4进行分析，可以看到不同硬点、不同水平的坐标值对悬架跳动性能质量特性均值和信噪比的影响。响应值越小，说明悬架性能越好；信噪比越大，说明悬架性能的稳健性越高。综合考虑均值和信噪比，得到最后的优水平组合如表3所示。

表3 优水平组合

2.6 基于蒙特卡罗的稳健性优化结果分析

根据田口稳健性优化结果，对优化前后的悬架跳动力学性能进行分析，结果如表4所示。从表4可以看出，前束角、外倾角、主销后倾角和主销内倾角的变化率均有所下降，优化百分比均在20%以上，说明悬架的运动学性能有了较大提高。证明了优化结果的有效性。

表4 优化结果分析

同时，采用蒙特卡罗方法对优化前后的稳健性进行进一步分析。蒙特卡罗方法是一种利用重复的统计试验来求解物理和数学问题的方法，用随机过程来描述随机变量，统计得到均值以及方差分布［13］。本文采用简单随机抽样方法将优化前后模型进行蒙特卡罗验证，采样点取600，结果如图5所示。

由蒙特卡罗验证结果可以看出，在车轮上下跳动过程中，前束角、外倾角、后倾角和主销内倾角的变化值均有较大的下降，表明悬架整体性能有了很大的提高；同时在考虑一定的硬点误差时，各响应的方差也有所减小，表明由于悬架硬点误差的影响导致的悬架性能参数的波动也大大减小，优化后的悬架稳健性有了很大提高。

图5 优化前后目标函数概率分布

3 结束语

通过对某电动车麦弗逊独立悬架进行稳健性优化，得到了以下结论：

a.建立麦弗逊独立悬架空间运动的数学模型，并通过与实验数据对比，证明该模型能很好地近似原实车悬架，采用该模型大大减少了稳健性优化过程中的计算量。

b.采用田口稳健性优化方法对麦弗逊悬架进行稳健性优化设计，优化后的悬架性能有了很大提高，同时稳健性也大大提高。

［1］ Hurel J，Mandow A，García-Cerez A.Kinematic and dynamic analysis of the McPherson suspension with a planar quarter-car model［J］.Vehicle System Dynamics，2013，51（9）：1422-1437.

［2］ 胡宁，罗素云，陈志恒，等.麦弗逊悬架运动分析的空间解析法［J］.拖拉机与农用运输车，2007，34（3）：6-7.

［3］ 陆建辉，周孔亢，郭立娜，等.电动汽车麦弗逊前悬架设计及参数优化［J］.机械工程学报，2012，48（8）：98-103.

［4］ Chatillon M M，Jezequel L，Coutant P.Hierarchical optimisation of the design parameters of a vehicle suspension system［J］.Vehicle System Dynamics，2007，44（11）：817-839.

［5］ 秦伟，耿庆松，黄勇刚，等.某车型麦弗逊转向悬架分析和优化设计［J］.农业机械学报，2014，45（10）：15-20.

［6］ 丁飞，韩旭，刘桂萍，等.悬架导向机构硬点灵敏度分析及多目标优化设计［J］.汽车工程，2010，32（2）：137-142.

［7］ 王涛，陶薇.考虑随机因素的汽车悬架参数多目标稳健优化［J］.振动与冲击，2009，28（11）：146-149.

［8］ Kang D-O，Heo S-J，Kim M-S.Robust design optimization of the McPherson suspension system with consideration of a bush compliance uncertainty［J］.Journal of Automobile Engineering，2010，224（6）：707-716.

［9］ Zang C，Friswell M I，Mottershead J E.A review of robust optimal design and its application in dynamics［J］.Computers and Structures，2005，83（4／5）：315-326.

［10］ 莫旭辉，赵宇航，钟志华，等.基于6σ稳健性方法的汽车行驶平顺性优化［J］.中南大学学报：自然科学版，2012，43（11）：4286-4292.

［11］ 刑天伟.基于田口方法的整车平顺性仿真及优化［D］.长春：吉林大学，2008.

［12］ 张代胜，张旭，王浩，等.基于Taguchi方法的动力总成悬置系统稳健优化［J］.汽车工程，2014，36（4）：475-480.

［13］ 谢展，于德介，李蓉.汽车发动机悬置系统的多目标稳健优化设计［J］.汽车工程，2013，35（10）：893-897.

Robust Design Optimization of the Automotive McPherson Suspension Based on Taguchi Method

ZHANG Ying1，WU Guangqiang1，2
（1.School of Automotive Engineering，Tongji University，Shanghai 201804，China；2.Institute of Industrial Science，University of Tokyo，Tokyo 153-8505，Japan）

针对悬架设计制造过程中存在不确定性因素而带来性能不稳定的问题，对某电动车麦弗逊悬架进行空间运动学分析，建立了求解悬架性能参数的数学模型，并通过试验验证了模型的合理性利用该数学模型，采用田口稳健性设计方法，进行正交试验设计，对悬架跳动力学特性进行了多目标稳健性优化，将优化结果进行蒙特卡罗验证，结果表明，优化后的悬架性能及其稳健性均有了很大提高。

稳健性优化；田口方法；正交试验；蒙特卡罗法

In view of the problem of uncertainty factors in suspension design and manufacture，which leads to unstable performance，based on spatial analytic geometryand multi-body dynamic method，spatial kinematics analysis is carried out on the suspension and a mathematic model of the suspension performance is built，and the model is verified by tests．Using this mathematic model，the multi-objective robust optimization design of suspension is carried out by using Taguchi method and orthogonal experiment design．The results show that the dynamic performance and robustness of optimized suspension is greatly improved，which has been validated by Monte Carlo method．

robust optimization；Taguchi method；orthogonal experiment；Monte Carlo method

U462.3

A

1001-2257（2015）09-0003-05

张 瑛（1990－），女，安徽安庆人，硕士研究生，研究方向为整车动力学分析与优化；吴光强 （1965－），男，上海人，教授，博士研究生导师，研究方向为汽车先进设计与仿真，汽车多体系统动力学与非线性控制等。

2015-04-10

国家重点基础研究发展计划（“九七三”计划）（2011CB711200）