高频电压频率附加误差线性回归修正及其不确定度分析

赵海鹰

(92493信箱89分箱，葫芦岛 125000)



高频电压频率附加误差线性回归修正及其不确定度分析

赵海鹰

(92493信箱89分箱，葫芦岛 125000)

本文针对高频电压表频率附加误差检定中示值定度偏差问题进行了探讨和分析,提出了修正措施，并对修正数据进行不确定度评定。

电压；频率附加误差；线性回归；不确定度

0 引言

频率附加误差是高频电压测量仪表最基本的计量检定项目，通常采用“固定被检读标准”的方式进行检定。操作过程发现，由于高频信号源输出电压调节灵敏度不够高，或电压表的分辨力较低，常常会使被检表不能准确地指示于要求的定度电压指示值上，从而引入测量误差。本文针对检定过程中存在的被检仪表定度电压示值偏差问题进行讨论与分析。

1 频率附加误差的检定

1.1 频率附加误差检定系统

频率附加误差是指在规定的环境条件和技术条件下，电压表所测量的电压值偏离定度频率时的测量值所产生的附加误差。频率附加误差检定用计量标准通常采用交直流替代原理，将高频电压转换为直流电压进行测量，例如ZC-100B高频电压标准装置，用其组建的电压表频率附加误差检定系统如图1所示。

图1 电压表频率附加误差检定系统

电压表频率附加误差检定方法与步骤是:

1)按照检定规程的要求，将高频信号源的频率调整到被检电压表的定度频率点上，调节其输出幅度大小，使被检表指示于要求的定度电压值，由ZC-100B读取定度频率点的实际电压测量值。

2)将高频信号源的频率调整到被检电压表的检定频率点上，调节其输出幅度大小，使被检表示值保持不变，由ZC-100B读取各检定频率点的电压测量值。

根据式(1)计算被检表的频率附加误差：

(1)

式中，U0为定度频率点上电压实际值；Uf为检定频率点上电压实际值。

1.2 频率附加误差检定指示偏差问题

图1所示系统是由激励用高频信号源与ZC-100B高频电压标准共同构成标准源，以检定R&S公司的URV35高频数字电压表为例介绍说明指示偏差问题，URV35频率附加误差的检定数据如表1所示。

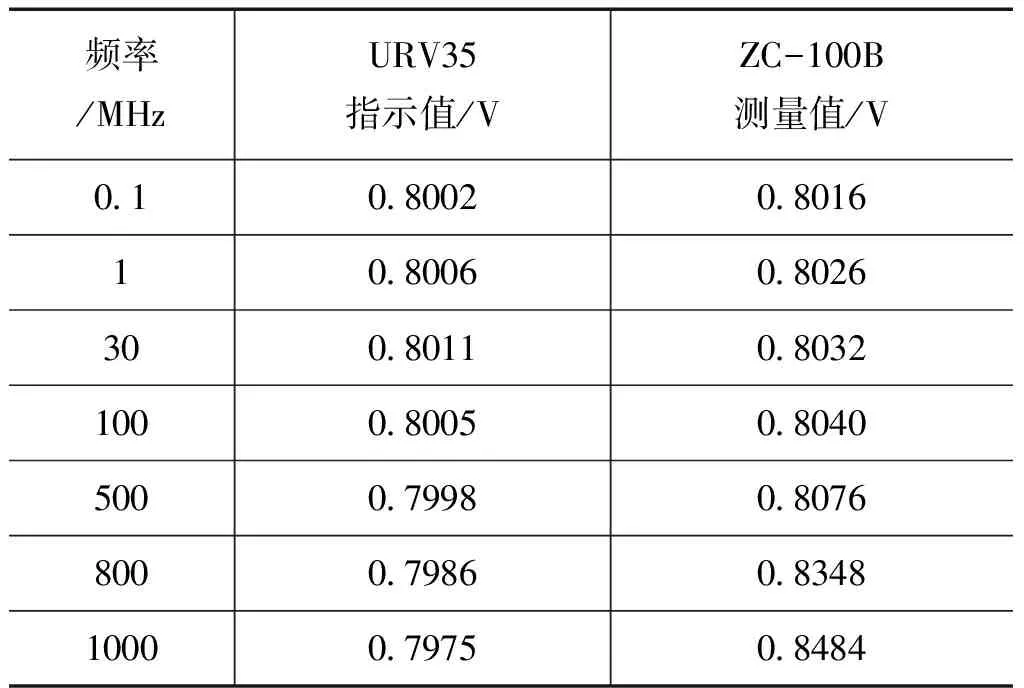
表1 URV35频率附加误差检定数据

表1的测试数据是根据规程要求，选择0.8V/100kHz为频率附加误差定度检定点。由于高频信号源输出电压分辨力的限制，URV35不能准确地指示为0.8V，只能接近于0.8V；改变信号频率，继续调整信号源输出幅度进行各频率点的检定，URV35仍然不能准确地指示为0.8V，而且也不再指示为定度频率时的0.8002V。忽略被检表URV35的指示偏差，根据式(1)计算URV35的频率附加误差时，如果直接引用定度点电压值0.8002V(U0)去计算频率附加误差是不完善的，这种指示偏差必然会给检定结果带来误差。

2 频率附加误差检定数据的修约

解决频率附加误差检定指示偏差问题最直接的方法是尽量选用幅度分辨力较高的信号源，使所有的被检电压表能够准确地指示在定度电压值。但对于高频甚至微波信号源，这是比较困难的，即使设备价格不是问题，对于建标用配套设备这种做法的费效比也低。采用线性拟合基本原理进行线性回归分析是计量学可以使用的最有效的实验数据处理方法。

2.1 一元线性回归分析

线性回归是一种有效的处理变量之间相关关系的数理统计方法。

一般地，对于两个变量x和y，理论上存在方程y=a+bx，则说x和y成线性关系或直线关系，如果通过实验可获知反映两个变量之间关系的一系列数据来确定方程系数a和b的值，即寻求两个变量之间的函数关系，就称其为一元线性回归。

这个步骤好似选择一条直线与这些实验测试点作最佳配合，故也称直线拟合。

2.2 频率附加误差检定数据的修正

由表1可知，由于高频信号源输出电压分辨力的限制，URV35不能准确地指示为定度电压0.8V，但是在某个频率点，可以调节信号源输出使URV35的显示值在要求的定度电压附近，测得几组对应的数值，然后进行建模,即进行直线拟合，从而预测当URV35的指示值为0.8V时的ZC-100B的数值。测量数据如表2。

表2 URV35频率附加误差检定数据

下面以表2的数据推导具体的直线拟合方程。x代表URV35的显示值，y代表ZC-100B的测量值，x与y一一对应，关系曲线如下：

y=a+bx

(2)

因为测量误差的存在，通过实验获得的数据显然不会全部通过所寻求的反映两个变量间函数关系的曲线；但是，由于x的取值尽量靠近定度电压值0.8V，可以把这一小段x与y的特性曲线以一条直线代替，按照误差最小的原则，以最小二乘法直线作为拟合曲线的模型，这是求系数a和b最佳估计值时最常用的有效方法。

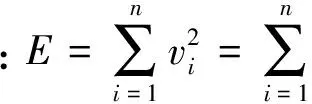
于是拟合曲线系数a和b应满足：

(3)

解方程组得：

(4)

(5)

把表2数据代入式(4)和式(5)得：

b=0.7769

a=0.1795

所以，表2中数据的直线拟合方程可表示为：

y=0.1795+0.7769x

(6)

那么，在100kHz频率点上，假设URV35的指示值为0.8V，ZC-100B的修约值为0.8011V。同样在其它的频率点上，按照上述方法对ZC-100B的测量值进行修正，修正后数据如表3；然后用修正后的数据根据式(1)计算被检表的频率附加误差。

表3 URV35频率附加误差检定数据修约值

3 检定数据修约值的不确定度分析

3.1 观测值的残余标准差

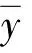
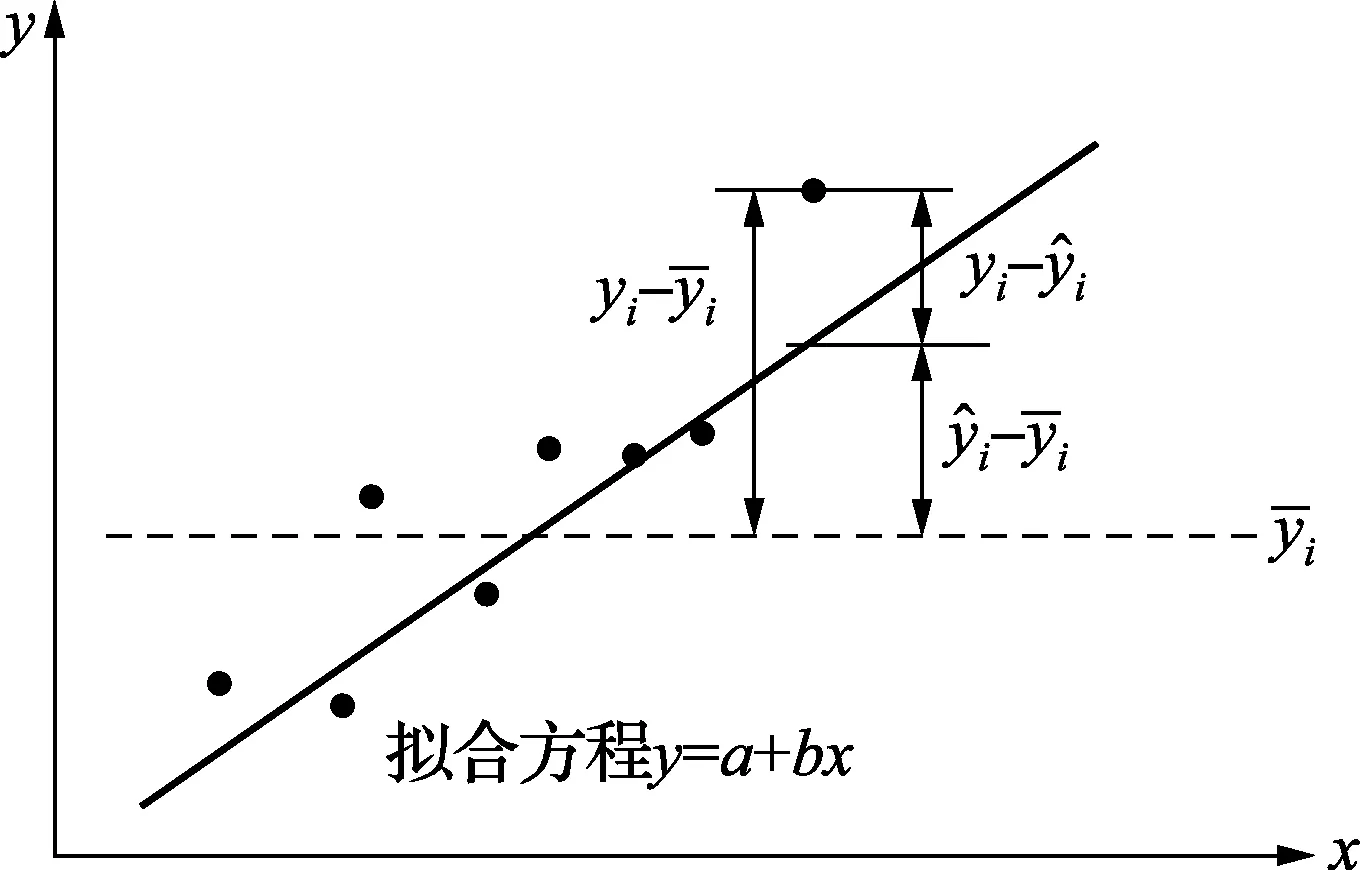
图2 直线拟合方程

(7)

式(7)中，Q为残余平方和，即所有观测点到拟合直线的残余误差的平方和，则残余标准差s为(Q的自由度ν=N-2)：

(8)

s用来表征所有随机因素对y的一次性观测的平均变差的大小。

3.2 回归系数的标准差

回归系数的标准差用来描述回归系数的分散性。根据式(4)和式(5)及方差的性质有：

(9)

所以回归系数b的标准差为：

(10)

同理，根据式(4)和式(5)及方差的性质有：

(11)

回归系数a的标准差为：

(12)

回归系数a和b的协方差为：

(13)

a和b的相关系数为：

(14)

3.3 回归方程的稳定性及拟合值的不确定度

根据不确定度传播公式及式(2)有：

(15)

式(15)中，u(a)、u(b)分别以回归系数a和b的标准差表示，即：

u(a)=s(a)，u(b)=s(b)

所以，将式(8)、式(10)、式(12)及式(14)代入式(15)计算得：

(16)

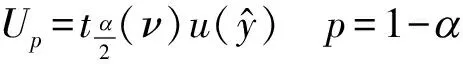
(17)

3.4 频率附加误差检定数据修约值的不确定度

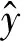
=0.00022

(p=0.95,ν=8)

4 结束语

本文详细介绍了高频电压频率附加误差检定数据偏差的线性回归修正方法及其不确定度分析，所举例中回归曲线或参数及相关标准差和不确定度的计算可利用Excel中函数、Matlab等工具或软件方便快速求得。对于计量校准实践中，由于标准或设备分辨率限制使被检仪表不能准确地定度到所要求的固定数值而需要进行数据修正具有参考意义。

[1] 盛骤，等.概率论与数理统计[M].北京：高等教育出版社，2001

[2] 国家质量监督检验检疫总局．JJF 1059.1—2012测量不确定度的评定与表示，2013

[3] 沙定国．误差分析与测量不确定度评定示[M].北京：中国计量出版社，2003

[4] 吴石林，等．误差分析与数据处理[M].北京：清华大学出版社，2010

[5] 梁晓东，安芳红．高频电压计量中频率附加误差检定的探讨和分析[J].计量技术，2006(12)

[6] 金正一，李凤岐．一元线性参数最小二乘法中斜率及截距的不确定度[J].沈阳工业学院学报，2000(19-1)

[7] 钱绍圣．测量不确定度[M].北京：清华大学出版社，2002

[8] 肖明耀.误差理论与应用[M].北京:中国计量出版社，1985

10.3969/j.issn.1000-0771.2015.4.13