0.1级钟罩式气体流量标准装置的不确定度分析

邢静芳 毕丽新 牛立娜 陈世砚

(河北省计量监督检测院，石家庄 050051)



0.1级钟罩式气体流量标准装置的不确定度分析

邢静芳 毕丽新 牛立娜 陈世砚

(河北省计量监督检测院，石家庄 050051)

在尺寸测量方法的基础上，结合现代传感技术和高准确度等级的测量仪器，实现了对0.1级2000L钟罩式气体流量标准装置标准状态下瞬时流量的校准，确定了不确定度来源，进行了不确定度分析。

钟罩；气体流量；不确定度；温压补偿；传感器

0 引言

钟罩式气体流量标准装置(以下称标准装置)作为原级气体计量标准应用广泛。我院协同有关单位研制了扩展不确定度小于0.1%的2000L标准装置。使用现代传感技术和高准确度等级的测量仪器检测标准装置的容积、时间、温度和压力，进行标准装置的不确定度分析。

1 测量原理

在温度为(20±1)℃、最大允许误差为±0.1℃的恒温实验室环境中，测量出钟罩排出气体的体积、时间、压力和温度，计算出排出钟罩的气体累积流量和瞬时流量。

2 数学模型

qN=VN/t

(1)

VN=VsPTN/(PNTZ)

(2)

Vs=sV

(3)

式中：qN为标况条件下标准装置的气体流量，m3/h；VN为标况条件下标准装置内的气体体积，m3；Vs为流经标准装置的气体体积，m3；t为测量时间，s；P为工作时钟罩内气体绝对压力，Pa；T为钟罩内气体绝对温度，K；Z为在P，T下的气体压缩系数，为一常数；PN为标准大气压力，101.325kPa；TN为标况下钟罩内气体的绝对温度，293.15K；s为其他因素导致的重复性系数；V为钟罩的标准体积，m3。

3 不确定度传播率

由式(3)可得：

(4)

4 输入量的标准不确定度分析

4.1V的相对标准不确定度分量urel(V)

V=0.25pd2h[1+2aB(θ-20)]

式中：d为钟罩的内径，m；h为钟罩垂直移动的距离，m；aB为罩体材料的线性膨胀系数，aB=16.2×10-6m/℃；θ为检定时罩体的温度，℃。

令W=1+2aB(θ-20)，则：

(5)

4.1.1d引入的相对标准不确定度分量urel(d)

d由激光跟踪仪测量，为1.4m，其最大允许误差为±0.05mm，按矩形分布考虑，可得：

urel(d)=u(d)/d=2.062×10-3%

4.1.2h引入的相对标准不确定度分量urel(h)

h由光栅传感器测量，为1.3m，其分辨力为5μm，按矩形分布考虑，可得：

urel(h)=u(h)/h=1.110×10-4%

4.1.3θ引入的标准不确定度分量urel(θ)

θ由温度传感器测量，为20.1℃，其最大允许误差为±0.02℃，按矩形分布，可得：

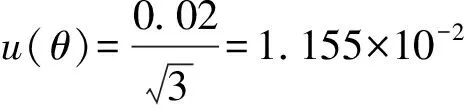
综上所述，由式(5)得：urel(V)=4.126×10-3%。

4.2 重复性引入的相对标准不确定度分量urel(s)

下列因素可导致测量重复性误差，其引入的相对标准不确定度为urel(s)：

(6)

4.2.1 Δp引入的相对标准不确定度分量urel(Δp)

urel(Δp)=ΔV/V=Δp/(101325+p)

式中：钟罩压力波动Δp=8Pa；钟罩余压p=2700Pa；ΔV为钟罩压力波动产生的钟罩体积变化，m3。所以urel(Δp)=7.690×10-3%。

4.2.2 余压引入的相对标准不确定度分量urel(ε)

钟罩罩体是一个薄壁圆筒形容器，在工作时由于余压的影响会使钟罩发生形变，最终导致钟罩的体积发生变化，形变后的体积为：

式中：Vp为余压导致钟罩变形后的体积，m3；E为罩体材料(304不锈钢)的弹性模量，Pa；δ为罩体壁厚，m；μ为罩体材料的泊松比。

已知：d=1.4m，E=1.95×1011Pa，δ=0.003m，p=2700Pa，μ=0.25，所以，urel(ε)=3.647×10-4%。

4.2.3 罩体横截面为椭圆引入的相对标准不确定度分量urel(g)

钟罩罩体在加工或运输过程中由于外力作用导致其横截面由标准圆变为椭圆产生体积误差。

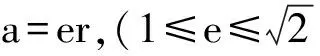
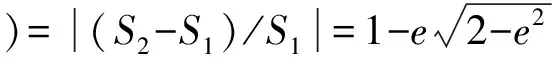
4.2.4 倾角a 引入的相对标准不确定度分量urel(a )

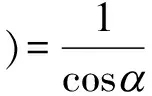
4.2.5 密封液附壁引入的相对标准不确定度分量urel(β)

标准装置在工作时导致密封液附在钟罩内外壁上，尤其是大流量时，密封液(采用油密封)附壁产生的油膜体积较大，为：

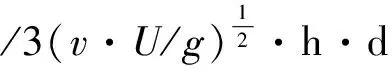
VZ=Vl[Si·(1+2δ/d)-S0]/(Si+S0)

式中：Vl为密封液附壁产生的油膜体积，m3；v为密封液的粘度，m2/s；U为大流量时钟罩上升的速度，m/s；Vz为钟罩上升停止后密封液挂壁产生的油膜净体积，m3；Si为钟罩内壁和干槽之间的环形面积，m2；S0为液槽和钟罩外壁之间的环形面积，m2。

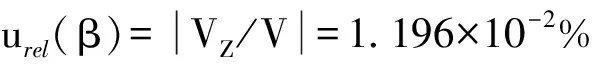
综上由式(6)可得，urel(s)=2.090×10-2%。

4.3P引入的相对标准不确定度分量urel(P)

P=p0+p

式中：p0为检定现场的大气压力，Pa。

u2(P)=u2(p0)+u2(p)

4.3.1p引入的标准不确定度分量u(p)

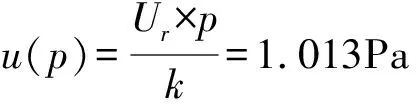
4.3.2p0引入的标准不确定度分量u(p0)

p0采用大气压力传感器测量，为100720Pa，其最大允许误差为±40Pa，属于B类不确定度,按矩形分布计算，所以，

=2.235×10-2%

4.4 T引入的相对不确定度分量urel(T)

T=t0+273.15℃

式中：t0为钟罩内气体温度，℃。

u2(T)=u2(t0)

t0采用温度传感器测量，为20.1℃，其最大允许误差为±0.1℃，按矩形分布，可得：

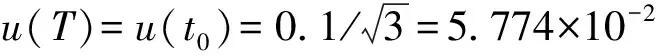
urel(T)=u(T)/T=1.969×10-2%

4.5t引入的相对标准不确定度urel(t)的分析

urel(t)为计时器分辨力引入的相对标准不确定度分量，计时器的分辨力为1ms，最短测量时间为t=60s，按均匀分布，所以，

urel(t)=u(t)/t=4.811×10-4%

5 合成不确定度和扩展不确定度

装置的标准不确定度汇总表见表3，合成相对不确定度由式(4)得：

urel(qN)=0.037%

k=2，置信概率为95%时相对扩展不确定度：

Urel(qN)=kurel(qN)=0.074%

6 结束语

本文对已研制的高准确度等级钟罩式气体流量标准装置的不确定度进行了全面的分析和评定，装置的扩展不确定度Ur=0.074%，k=2，满足0.1级准确度等级的要求。因此可以利用该装置开展高准确度等级气体流量计的检定与校准工作。

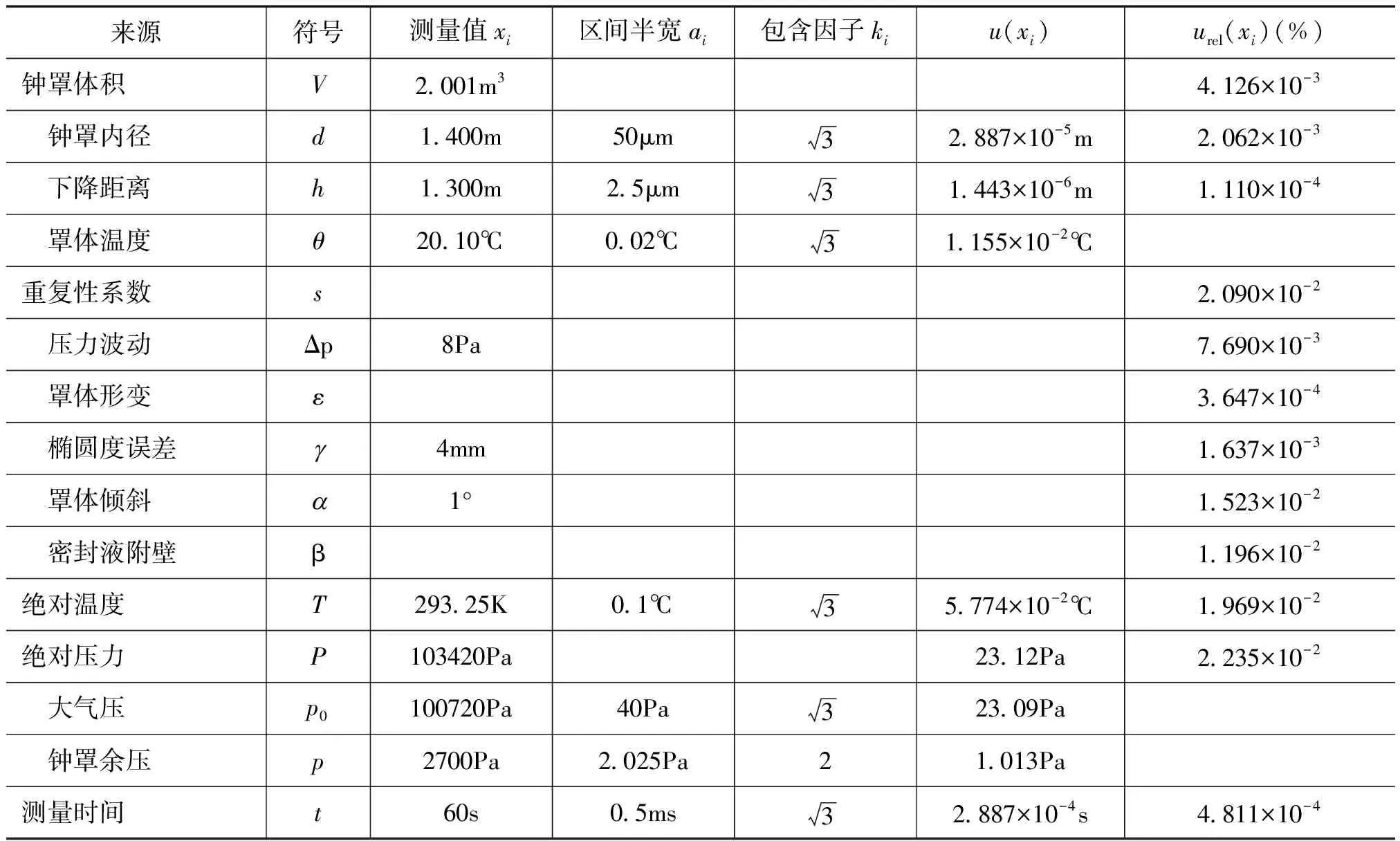
表3 标准装置主要标准不确定度汇总表

[1] 王自和,范砧.气体流量标准装置.北京：中国计量出版社，2005

[2] 李旭,崔骊水,孟涛,徐英华.基于尺寸法的标定钟罩式气体流量标准装置的新方法.计量技术，2008(9):42-45

[3] 李慎安,施昌彦,刘风.JJG 1059—1999测量不确定度评定与表示

[4] John D Wright and George E Mattingly.NIST Calibration Services for Gas Flow Meters Piston Prover and Bell Prover Gas Flow Facilities.National Institute of Standards and Technology,1998

[5] Hae Man Choi,Kyung-Am Park,Youn Kyun Oh,Yong Moon Choi.Uncertainty evaluation procedure and intercomparison of bell provers as a calibration system for gas flow meters.Flow Measurement and Instrumentation,2010

10.3969/j.issn.1000-0771.2015.4.21