超声共振频谱法测量固体材料的弹性模量*

鲍 静 冯晓娟 林 鸿 张金涛 齐晓风 李小亭

(1.河北大学质量技术监督学院，保定 071002；2.中国计量科学研究院热工计量科学研究所，北京 100029)



超声共振频谱法测量固体材料的弹性模量*

鲍 静1,2冯晓娟2林 鸿2张金涛2齐晓风1,2李小亭1

(1.河北大学质量技术监督学院，保定 071002；2.中国计量科学研究院热工计量科学研究所，北京 100029)

弹性模量是工程材料重要的性能参数，是反映材料抵抗弹性变形能力的指标。弹性参数是温度的函数，准确测量变温环境下固体材料的弹性参数，对热工、材料、航空航天、工业应用方面有非常重要的意义。然而，国内缺乏变温环境下准确测量固体材料弹性参数的仪器。本文基于超声共振频谱法原理，研制了可在变温条件下工作的超声共振频谱法测量系统，系统包括超声传感器、声学发射和接收系统、恒温系统以及数据采集和分析系统。在30℃下分别测量了四种不同能量品质因数(Q值)的固体材料的弹性参数，测量的共振峰匹配误差(RMS)可小于0.04%，与国外先进商业仪器的测量结果有良好的一致性，对超声信号激励和接收方式做相应改变，可扩展该装置的测温范围。

弹性模量；超声共振频谱；固体材料

0 引言

弹性模量是指当有力施加于物体或物质上时，其弹性变形(非永久变形)趋势的数学描述，是反映材料抵抗弹性变形能力的指标，是工程材料重要的性能参数。弹性参数是温度的函数，准确测量变温环境下固体材料的弹性参数，对热工、材料、航空航天、工业应用方面有非常重要的意义。弹性模量主要包括剪切模量、杨氏模量和体积模量等，三种模量均为材料的力学性能指标。

常用的测量固体材料的弹性模量的方法有很多种，如纵波共振法[1]、超声脉冲回波法[2]、脉冲激励法(IE)、四点弯曲法(4PB)、超声共振频谱法[3](RUS)等，其中RUS法具有最高的精确度和重复性[3]。超声共振频谱法的首次描述是在1987年[4]，它是一种测量固体弹性模量的技术和方法，通过测量固体材料的超声共振频率，得到高Q值、小尺寸的硬质材料的弹性模量[5]，因为RUS测量的是小尺寸固体的动态谐振频率，测量时对被测样品施加连续的频率激励[6]，属于超声波范畴，所以它不适合测量静态和低频的材料[7]。

目前，国内仅有常温条件精密测量固体弹性参数的商业仪器。因此，本文根据RUS的测量原理，设计了温度可变的测量固体弹性模量的实验装置，并用该装置对四种不同Q值的固体材料在30℃下的弹性参数进行了实验测量和分析，并将测量结果与国外先进商业仪器进行测量对比，得到了四种固体材料的杨氏模量、剪切模量和体积模量。

1 测量装置

为了满足变温需求，本文基于RUS的技术原理，设计了环境温度可变的固体材料弹性参数测量装置，如图1所示。

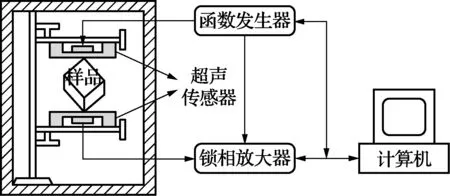
图1 弹性模量测量装置示意图

实验系统主要包括可控气体介质和温度的恒温箱，三维样品支架，超声传感器，声学发射和接收系统，以及仪器自动控制与数据采集分析系统。左侧为带有标尺的可X、Y轴调节的三维样品支架，可用于固定不同尺寸的样品，实验采用高性能锆钛酸铅压电陶瓷(PZT)自行研制了超声传感器，PZT的自然振动固有频率远高于其工作频率，从而避免了被测样品谐振时PZT会随着样品一起谐振的现象，其中发射端传感器属于大功率发射型PZT，接收端传感器属于高灵敏度接收型PZT。实验样品、支架和超声传感器置于可控气体介质和温度的恒温环境内。空气恒温槽的控温范围是-20～80℃，空气恒温槽由制冷恒温槽辅助控温。

实验系统中的函数发生器Aglient33220A产生的高频正弦激励信号作用于发射端传感器上，高频信号在被测样品中进行传播，接收端传感器从被测样品接收信号，输出至高频锁相放大器SR844，当频率变化至被测样品某个自然谐振频率时，被测样品发生共振，系统可获得一个较大的信号峰值，峰值所对应的频率即为样品的谐振频率。不断改变激励信号的频率，就可以获得样品的多个谐振频率。整个实验系统由计算机进行编程控制，包括对函数发生器和对锁相放大器参数的设置和信号的采集处理。

2 测量原理

利用莱温伯格-麦夸特法，由测量的谐振频率反推计算弹性模量。Migliori[8]对这个反推算方法进行了详细描述，计算方法的核心是对样品的若干个谐振频率的计算值和测量值进行匹配，在不断改变估计的弹性常数的情况下，尽可能减小测量的谐振频率的计算值与测量值之间的差异，当两者的匹配达到理想状态时，频率的计算值所对应的弹性模量即为最佳的弹性模量值。

对于线性固体材料而言，应力和应变之间存在如下关系：

σij=Cijkmεkm

(1)

其中ε和σ是应力和应变的弹性张量，C有81个元素[9]，对于各向同性材料，C可以由C11、C12两个常数表示，且存在如下关系式：

(2)

(3)

(4)

其中，E代表杨氏模量，G代表剪切模量，K代表体积模量。对各向同性材料，由RUS测量方法可以得到C11、C12，因此可以通过式(2)、(3)、(4)计算三种弹性模量的值。

3 实验结果与讨论

本文在30℃下对316L奥氏体无磁不锈钢、轴承钢、无氧铜和氧化铝固体材料的弹性常数进行了测量，四种材料都是各向同性介质，各端面平面度为0.0001～0.0003mm，表面粗糙度为0.012mm，端面间表面平行度为0.001～0.0015mm，样品的名义参数如表1所示。

在30℃下，对轴承钢进行扫频，可以得到如图2所示的频谱，用同样的方法对以上四种固体样品进行测量，并通过共振频率得到其体积模量K，测量结果示于图3。

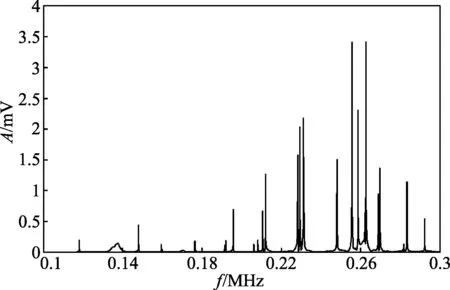
图2 轴承钢扫频图像

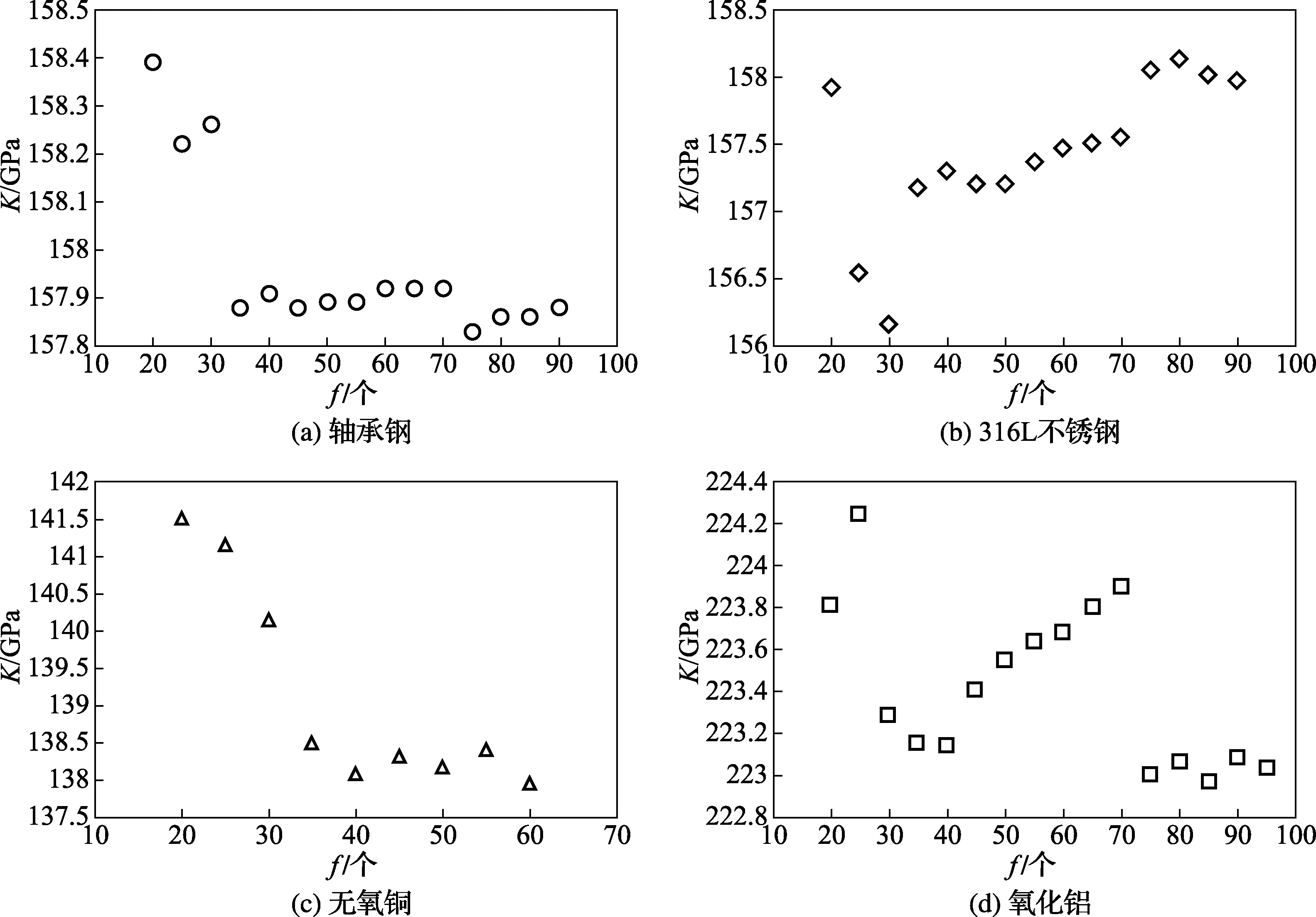
图3 四种样品的体积模量K随频点数的变化关系

图3中横坐标代表的是参与匹配的谐振频率的个数，纵坐标代表四种材料的体积模量值。从图3中可以看出，对于轴承钢而言，匹配个数小于30，测量结果表现出与匹配的谐振频率个数相关；匹配的频率个数大于30，测量结果出现与匹配个数无关的坪台。当匹配的频率个数大于70后，测量结果发生跳变，这可能是因为谐振频率过大，超出压电陶瓷传感器的线性响应区间或样品晶格机械性能响应的线性区间。综合考虑测量的频点数和测量周期，选择轴承钢的最佳测量频率点数为40。同理，对于316L不锈钢、无氧铜和氧化铝，它们的最佳测量频点数分别为45、50、80。

在30℃下， RUSpec在中国的供应商，对上述轴承钢和无氧铜样品进行了测量，并与本实验系统在相同温度下的测量结果进行了对比，分别见表2、表3。

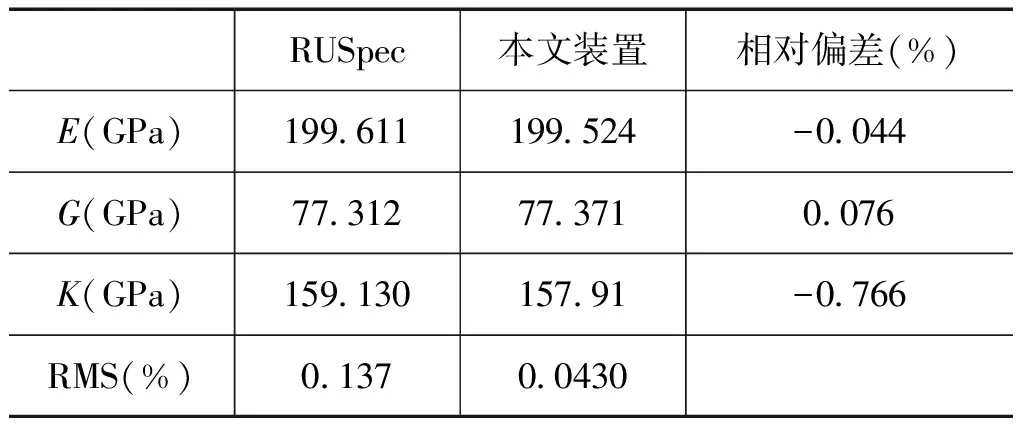
表2 轴承钢测量结果对比

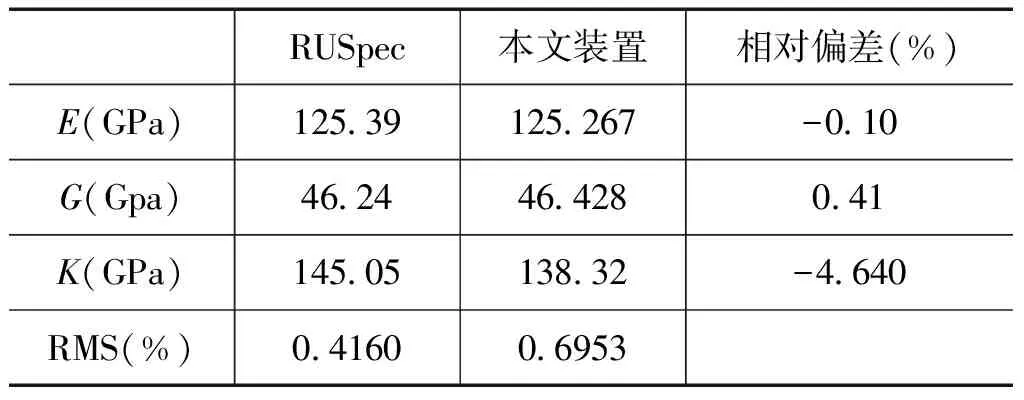
表3 无氧铜测量结果对比

对比结果显示，轴承钢和无氧铜的体积模量的相对偏差大于RUSpec声称共振峰匹配误差(RMS)，原因可能是商业仪器测量中选择的匹配频点数较少。对于轴承钢，图3显示，其频点数低于30，体积模量随频点数上升快速下降，频点数大于30，至坪台区，商业仪器选择的频点数是19。我们的研究显示，以该频点数测量得到的体积模量与频点数为40的测量结果间的相对偏差可达到-0.465%。对氧化铜而言，其频点数低于30，体积模量随频点数上升快速下降，频点数大于30，至坪台区。商业仪器选择的频点数是22，我们的研究显示，以该频点数测量得到的体积模量与频点数为50的测量结果间的相对偏差可达到4.50%。我们认为这是体积模量有较大相对偏差的主要原因。

在以上测量基础上，选择轴承钢、316L不锈钢、无氧铜和氧化铝的频率点数分别为40、45、50和80，可以得到在30℃下四种材料的杨氏模量E、剪切模量G和体积模量K，测量结果如表4所示。

表4 四种固体材料在30℃下的E、G、K的测量结果

4 结论

本文基于超声共振频谱法的原理，建立了固体材料弹性模量的测量装置，包括超声传感器、声学发射和接收系统、恒温系统以及数据采集和分析系统。本文对四种不同Q值的固体材料在30℃下的弹性模量进行了测量，得到了四种样品的杨氏模量、剪切模量和体积模量。测量装置的共振峰匹配误差RMS最小可达到0.04%，与当前先进的商用超声共振频谱仪器的结果对比，有良好的一致性。对超声信号激励和接收方式做相应改变，可用于更高温度的测量。

[1] 管珣，赵茂程，王正，等．基于纵向共振法测试杨树原木应力波波速及弹性模量的研究[J].西部林业科学，2013，42(2)：14-19

[2] 周世圆，陈磊，肖定国，等．超声弹性模量测量中声时测量精度的提高方法[J].传感器技术.2005,24(4)：42-45

[3] Radovic M, Lara-Curzio E, Riester L. Comparison of different experimental techniques for determination of elastic properties of solids[J]. Materials Science and Engineering，2004，A368:56-70

[4] Migliori A, Visscher W M, Brown S E, et al. Elastic constants and specific-heat measurements on single crystals of La2CuO4[J].Physical Review B, Condensed Matter,1990,41: 2098-2102

[5] Migliori A, Maynard J D. Maynard. Implementation of a modern resonant ultrasound spectroscopy system for the measurement of the elastic moduli of small solid specimens[J].Review of Scientific Instruments, 2005, 76,121301

[6] ASTM Standard C1198-96[S]

[7] Lee T, Lakes R S, Lal A. Resonant ultrasound spectroscopy for measurement of mechanical damping：comparison with broadband viscoelastic spectroscopy[J].Review of Scientific Instruments, 2000,71, 2855

[8] Migliori A, Sarrao J L, Visscher W M, et al. Resonant ultrasound spectroscopic techniques for measurement of the elastic moduli of solids[J]. Physica B, 1993, 183: 1-24

[9] Dowling N E. Mechanical Behavior of materials[M].2nd ed. Prentice Hall, 1998

*国家自然科学基金(57476153和51276175)

10.3969/j.issn.1000-0771.2015.4.04