考虑弹性变形的行星滚柱丝杠副滚滑特性

马尚君 刘 更 付晓军 佟瑞庭

(西北工业大学陕西省机电传动与控制工程实验室, 西安710072)



考虑弹性变形的行星滚柱丝杠副滚滑特性

马尚君 刘 更 付晓军 佟瑞庭

(西北工业大学陕西省机电传动与控制工程实验室, 西安710072)

为了揭示行星滚柱丝杠副滚滑机理,基于滚柱螺纹球面牙型特点,采用等效球的方法,分别建立了未考虑弹性变形和考虑弹性变形的行星滚柱丝杠副滚滑分析模型.通过求解两侧接触点的相对滑动速度,研究其滚滑特性.采用滑-滚比表征两接触侧滑动量与滚动量的相对关系,分别计算了两接触侧滑-滚比,并重点研究了螺纹结构参数中接触角、螺旋升角和滚柱螺纹牙数对两接触侧滑-滚比的影响规律.分析结果表明,考虑弹性变形,丝杠与滚柱接触侧会产生相对滑动,且两接触侧沿螺旋线切向产生的相对滑动速度最大;接触角和螺旋升角对两接触侧滑-滚比的影响趋势均相反,增大螺旋升角更有利于降低螺母侧滑-滚比;滚柱螺纹牙数对两接触侧滑-滚比的影响较小.

行星滚柱丝杠副;螺旋传动;滚动摩擦;弹性变形

行星滚柱丝杠副(planetary roller screw,PRS)是一种可将旋转运动转换成直线运动的传动机构.PRS主要由丝杠、螺母和多个滚柱组成,其传动原理是通过滚柱在丝杠和螺母螺纹滚道内做行星滚动来实现动力传输.由于PRS具有推力大、位置精度高和结构紧凑等优点,近年来广泛应用于全电飞行器[1-4]、武器装备[5-7]、医疗器械[8]和精密机床[9]等领域.但由于PRS的主要传力元件滚柱的自转轴线与螺纹牙受力方向成一定角度,滚柱的自转轴线受到约束,因此滚柱存在自旋滑动现象[10-11],也就是说,滚柱的行星运动是滚动与滑动并存.滑动成分的存在不但增大摩擦力矩,而且使滚柱与相啮合的螺母及丝杠表面产生摩擦热,引起接触表面温度升高,这会降低PRS的承载能力和定位精度,进而降低其传动效率.此外,PRS的结构较为复杂,而且对一个封闭系统很难进行滚滑试验测试.因此需要建立数学模型以预测其滚滑特性,进而指导其结构参数设计并提高传动性能.

Velinsky等[12]建立了考虑滑动的PRS运动学分析模型,研究结果表明丝杠和滚柱接触侧必然发生滑动,但其仅研究了丝杠一侧的滚滑特性.Hojjat等[13]对滚柱进行了受力分析,研究了螺纹旋向对滚动和滑动趋势的影响,得出了接触位置的变化是影响传动导程的主要因素的结论,并以实验进行了验证.靳谦忠等[10]和杨家军等[14]分别基于赫兹接触理论,研究了滚柱自旋滑动机理和预紧力与摩擦力矩的关系.陈小芬等[15]通过虚拟运动仿真,对滚柱自转转速及影响相对滑动的因素进行了分析.

本文根据PRS传动原理和多体接触特性,基于滚柱螺纹牙球面牙型特点,将滚柱螺纹牙等效成球体[16],考虑弹性变形分别计算丝杠侧和螺母侧接触点的相对滑动速度,研究其滚滑机理.在此基础上,采用滑-滚比表征两接触侧运动模式的差异性,重点研究螺纹牙结构参数对滑-滚比的影响规律.

1 PRS滚滑机理分析模型

1.1 PRS接触点位置分析

PRS中滚柱既自转又公转,其与丝杠和螺母的接触轨迹均为螺旋线,相对滑动速度可通过求解两接触侧接触点的速度差获得.为了便于速度求解,定义如图1所示3类坐标系.定义笛卡尔坐标系o-x′y′z′为固定坐标系,z′轴与丝杠轴线重合,单位向量为i′,j′,k′.定义坐标系o-xyz为旋转坐标系,固联于丝杠,z轴为丝杠轴线方向,其单位向量为i,j,k.定义滚柱等效球中心为o′点,其运动轨迹同为螺旋线,无弹性变形时,滚柱与丝杠和螺母的接触点分别为点B和点A(两点为发生变形后的椭圆中心),在o′点定义Frenet坐标系[17],其单位向量为t,n,b.在外荷载作用下,两接触侧均产生弹性变形并形成接触椭圆,在两侧接触点建立坐标系i-xiyizi(i=A,B),如图2所示,用于表示接触点的位置,其单位向量为ii,ji,ki,其中xiyi平面为接触椭圆所在平面,zi为接触椭圆法向.

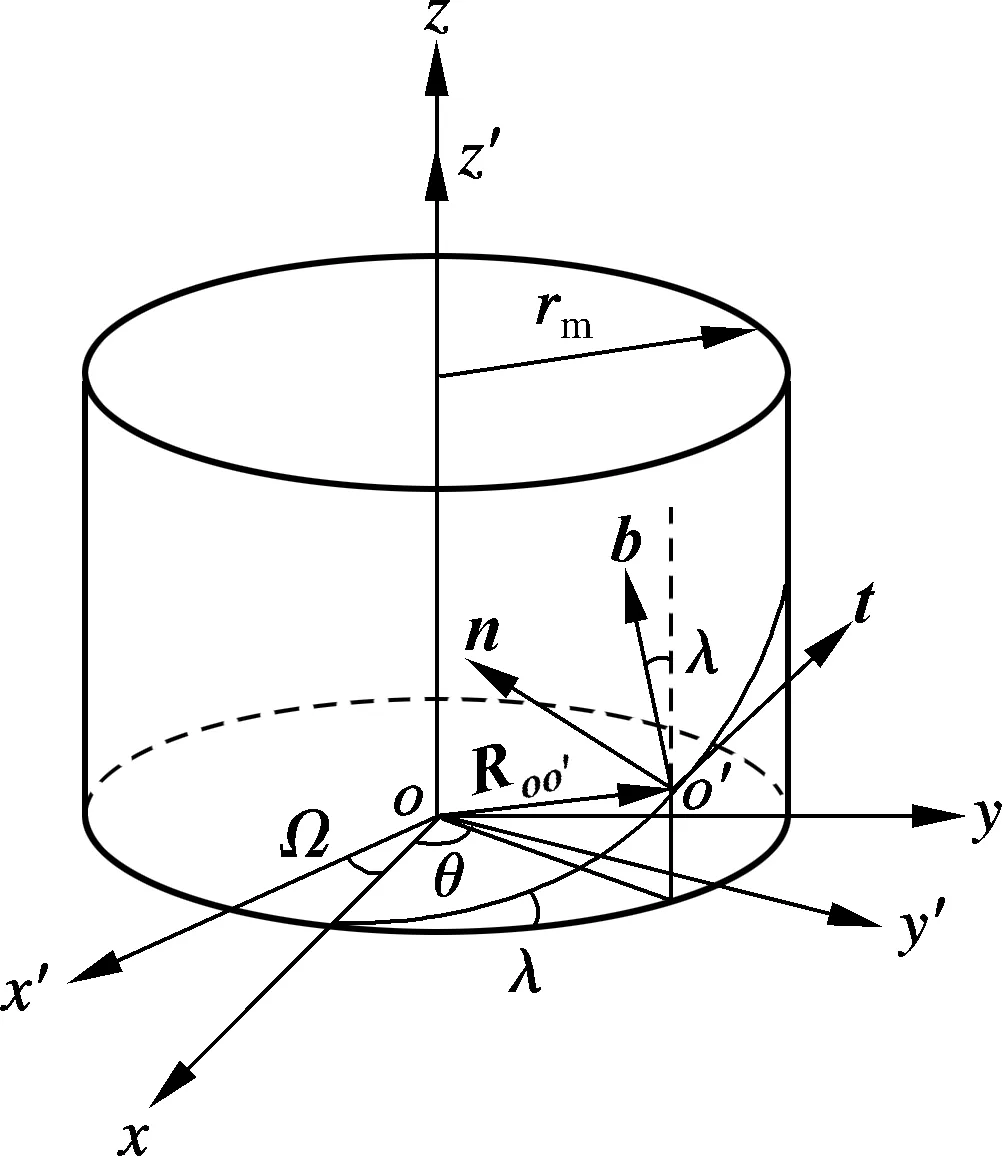
图1 PRS坐标系示意图

图1中,Roo′表示o到o′的向量,o到o′的距离用d表示,则d=rm/cosλ,rm为oo′在xy平面的投影长度.λ为螺旋升角,Ω表示o-xyz坐标系角位移,θ为o′点相对起点的旋转角.

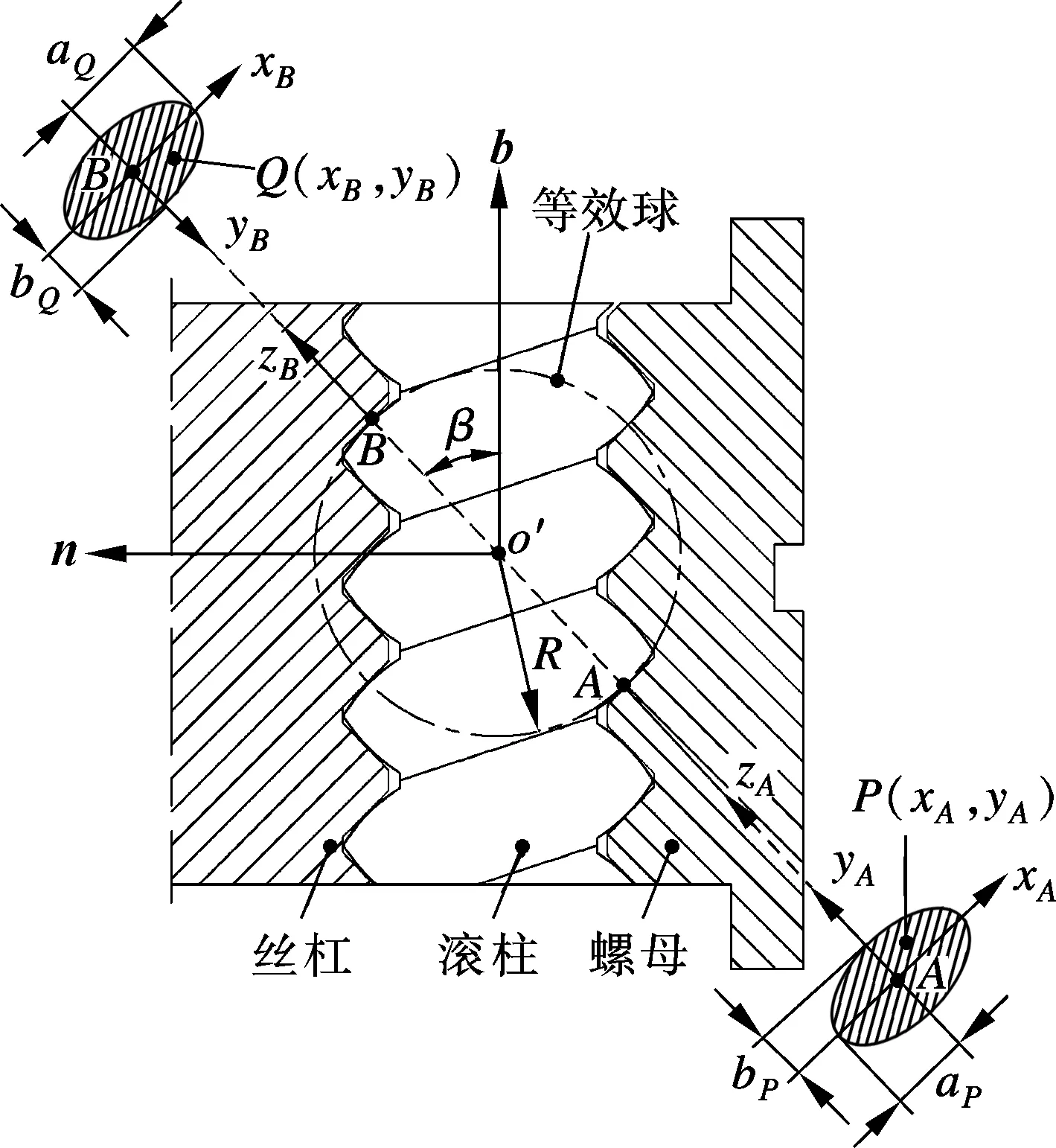
图2 等效球和弹性接触示意图

图2中,β为接触角,并假定滚柱与丝杠和螺母啮合过程中,螺纹牙接触角保持不变.R表示滚柱等效球半径,由下式给出:

(1)

式中,dr表示滚柱中径.根据坐标变换可知,坐标系o-x′y′z′和o-xyz的坐标变换为

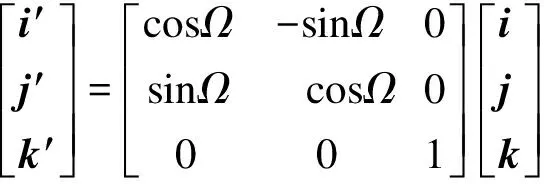
(2)

则滚柱等效球球心的位置向量可表示为

Roo′(θ)=rm(cosθi+sinθj+θtanλk)

(3)

Frenet坐标系的单位向量可采用旋转坐标系表示，即

t=-cosλsinθi+cosλcosθj+sinλk

(4)

n=-cosθi-sinθj

(5)

b=sinλsinθi-sinλcosθj+cosλk

(6)

则o-xyz坐标系与Frenet坐标系变换如下:

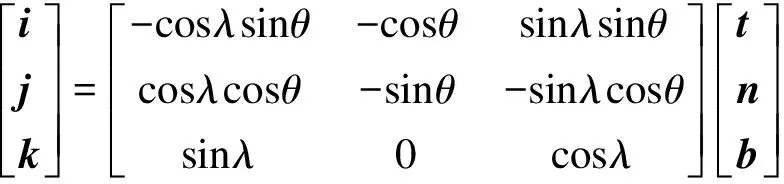
(7)

将式(7)代入式(3),滚柱等效球球心位置向量可改写为

Roo′=rm(θsinλtanλt-n+θcosλtanλb)

(8)

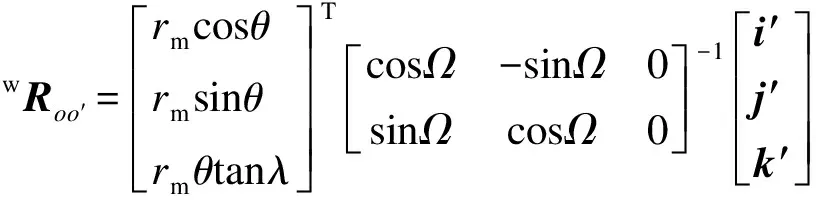
(9)

接触点坐标系i-xiyizi与Frenet坐标系变换为

(10)

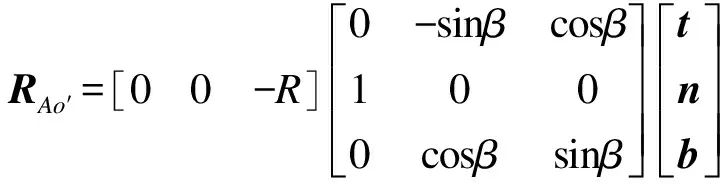
(11)

(12)

联立式(8)、(11)和(12),接触点相对于旋转坐标系的位置向量可表示为

RA=Roo′+RAo′

(13)

RB=Roo′+RBo′

(14)

1.2 滑动分析模型

在获得图2所示接触点位置向量后,即可通过位置向量对时间求微分，获得速度向量.故滚柱等效球球心的速度通过式(3)对时间求微分获得,即

(15)

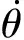
(16)

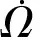
(17)

假定滚柱等效球球心在Frenet坐标系下的角速度为ω={ωt,ωn,ωb}{t,n,b}T,则接触点A的速度为

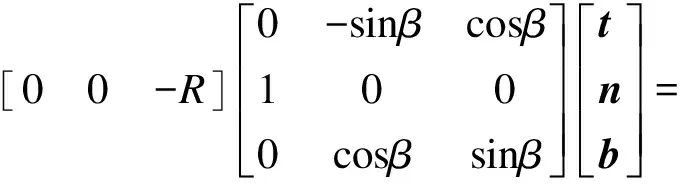
(18)

同理,接触点B的速度为

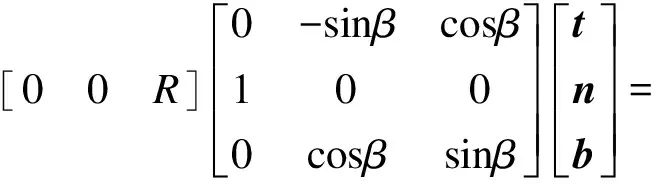
(19)

根据滚柱运动原理可知,在Frenet坐标系的3个坐标方向,滚柱只有绕b轴的角速度,即ωt=0和ωn=0,则式(18)和(19)改写为

(20)

(21)

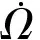
(22)

丝杠在接触点B的速度为

(23)

由式(20)和(22)可得接触点A的滑动速度为

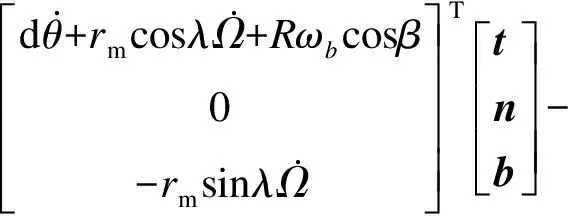
(24)

同理由式(21)和(23)可得接触点B的滑动速度为

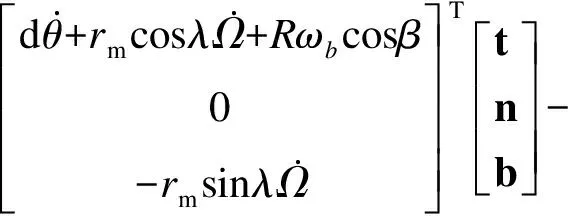
(25)

由式(24)和(25)可见,受制于安装和运动限制,在螺母侧接触点,螺母仅有沿轴向的直线运动,因此仅有沿螺旋线的相对滑动速度,而且螺母相对滚柱在轴向没有相对滑动,从而保证了螺母与滚柱无相对轴向位移,确保了螺母与滚柱正确啮合.在丝杠侧接触点,切平面发生相对滑动,且相对滑动速度的大小与接触角和螺旋升角直接相关.

1.3 考虑弹性变形的滑动分析模型

考虑弹性变形,接触点为椭圆内任意点,假定两侧接触椭圆内各有一点Q和P,如图2所示.点Q和P关于Frenet坐标系的位置向量分别为

(26)

(27)

产生弹性变形的两接触表面的曲率半径为

(28)

式中,rQ,s和rRQ分别为接触点B在丝杠侧和滚柱侧曲率半径;rP,n和rRP分别为接触点A在螺母侧和滚柱侧曲率半径.

(29)

(30)

则在两接触侧,弹性变形量在Frenet坐标系分别为

(31)

(32)

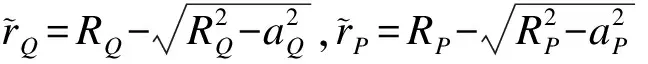
(33)

(34)

点Q和P关于固定坐标系的位置向量为

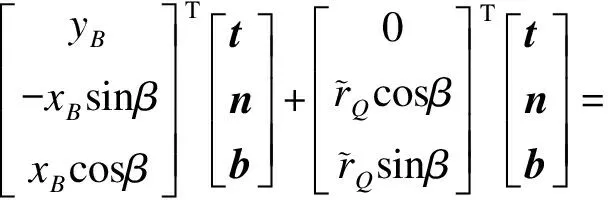
(35)

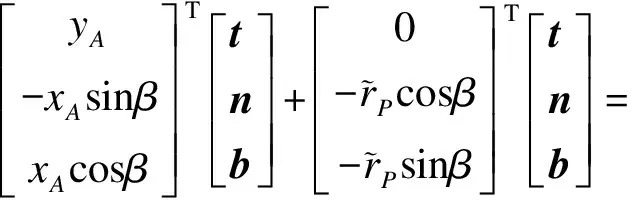
(36)

等效球在点Q和点P的速度分别为

(37)

(38)

螺母在点P的速度为

(39)

丝杠在点Q的速度为

(40)

则接触点Q和P的滑动速度分别为

Vs,Q=VQ,b-VQ,s=

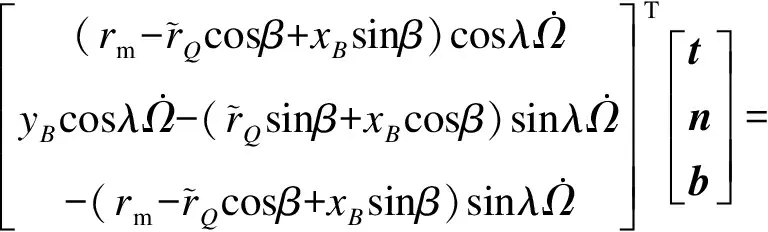
(41)

Vs,P=VP,b-VP,n=

(42)

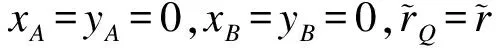
1.4 滑-滚比

在PRS的运动过程中,两接触面在接触点的速度不同,采用滑-滚比来表示滚动量和滑动量的相对关系,用于分析两接触面间运动模式的差异性.定义滑-滚比为[17]

(43)

式中,Vr为两接触面之间的滑动速度向量；Vdr为主动面速度向量；Vpr为从动面速度向量.在丝杠侧,接触点滑-滚比为

(44)

同理,在螺母侧滚柱为主动,螺母为从动,则接触点滑-滚比为

(45)

分别将式(37)～(40)代入式(44)和(45),可分别计算出两接触侧滑-滚比.

2 螺纹结构参数影响因素分析

根据PRS结构组成及其传动原理可知,螺纹结构参数的选择直接关系到传动机构的性能,如摩擦力矩、轴向刚度和传动效率等[18].故本文重点研究螺纹结构参数对PRS滚滑机理的影响规律,以期能够对PRS参数匹配设计提供参考.同时,根据滚柱螺纹牙的荷载分布关系,以承力最大螺纹牙为基准,接触点位置坐标取平均值,分别计算两接触侧弹性变形和滑-滚比.本文以德国LTK10吨级某型PRS为例,研究螺纹结构参数与滑-滚比的关系.其主要结构参数如表1所示.

表1 PRS结构参数

2.1 接触角对滑-滚比的影响

在PRS结构设计中,为了保证承载能力和尽量减小啮合间隙,丝杠、滚柱和螺母的接触角通常取相同值.保持丝杠转速3 000 r/min、滚柱螺纹牙数10和丝杠螺旋升角11.533°不变,研究接触角在不同轴向荷载作用下对两接触侧滑-滚比的影响规律.计算结果如图3所示.

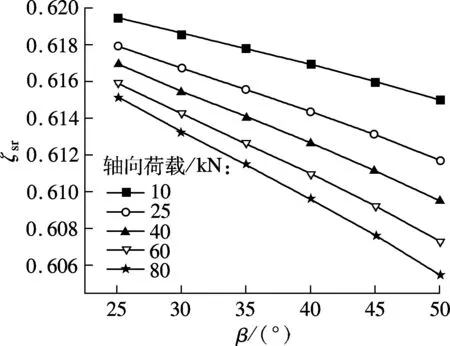
(a) 丝杠

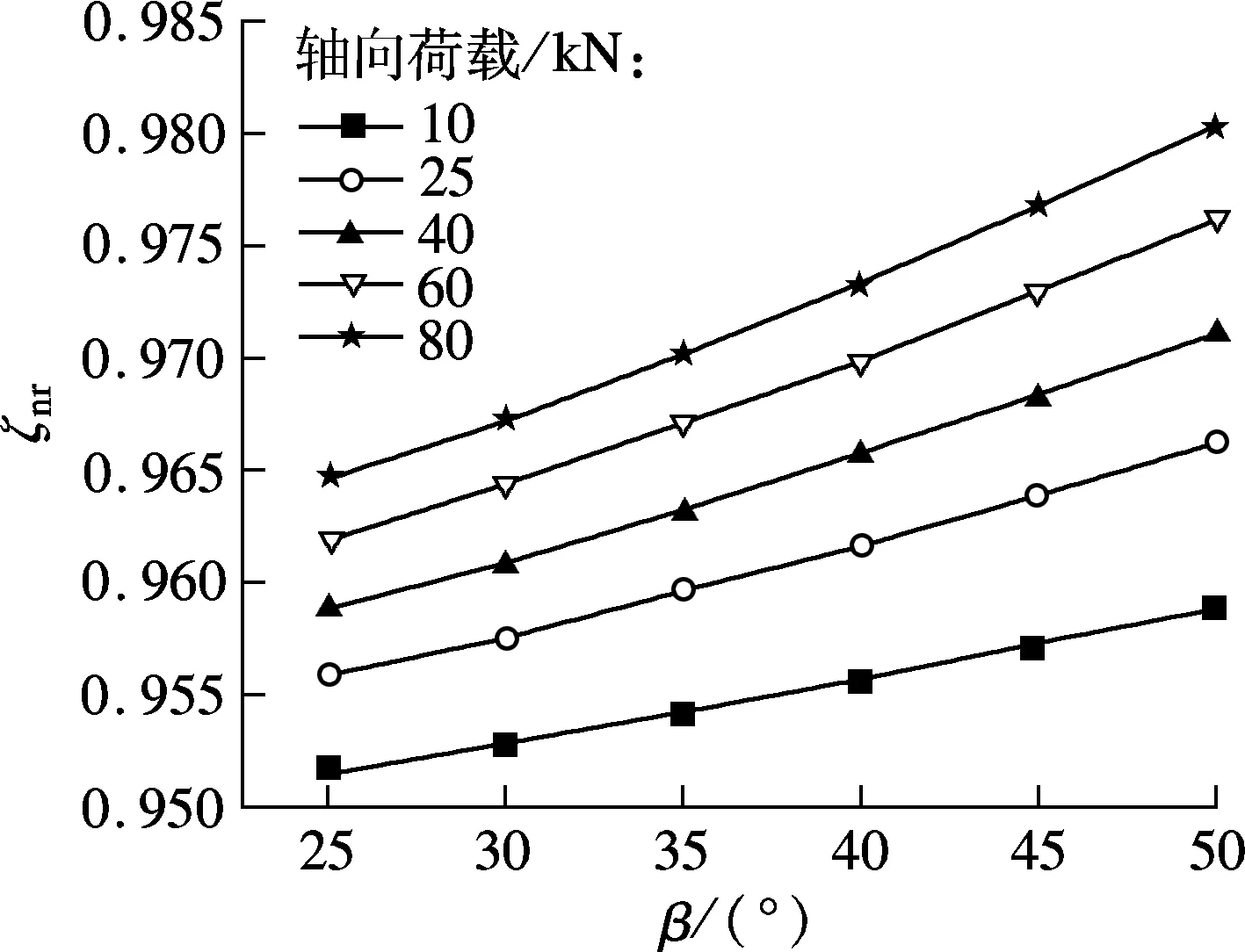
(b) 螺母

由图3(a)可见,相同轴向荷载下,随着接触角的增大,丝杠侧滑-滚比减小,且轴向荷载越大,滑-滚比减小幅度越大,这是因为接触角的变化引起滚柱螺纹牙法向荷载和等效曲率半径发生变化,能够有效降低摩擦力矩,进而减小滑动量.相同接触角下,随着轴向荷载的增大,滑-滚比减小,尽管减小幅度不大但对于提高传动效率非常有益.因此,对于丝杠侧而言,在相同丝杠转速下,接触角和轴向荷载越大越有利于PRS保持大推力和高传动效率.接触角对螺母侧滑-滚比的影响规律与丝杠侧的趋势相反,这是因为发生弹性变形后,丝杠侧接触表面的曲率半径和接触面积均小于螺母侧.对应于表1参数,在轴向力为80 kN、接触角为45°时,丝杠侧曲率半径为13.788 6 mm,螺母侧曲率半径为22.981 0 mm,丝杠侧接触面积为1.001 4 mm2,螺母侧接触面积为1.191 9 mm2,可见螺母侧接触点的坐标值较大,导致螺母侧滑-滚比大于丝杠侧,且轴向荷载和接触角越大,该侧滑-滚比越大.

2.2 螺旋升角对滑-滚比的影响

PRS的直线速度是衡量其传动性能的重要指标之一,保持接触角为45°、丝杠转速为3 000 r/min和滚柱螺纹牙数为10不变,研究不同丝杠螺旋升角对两接触侧滑-滚比的影响规律.计算结果如图4所示.

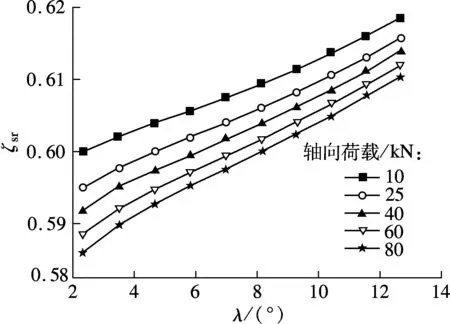
(a) 丝杠

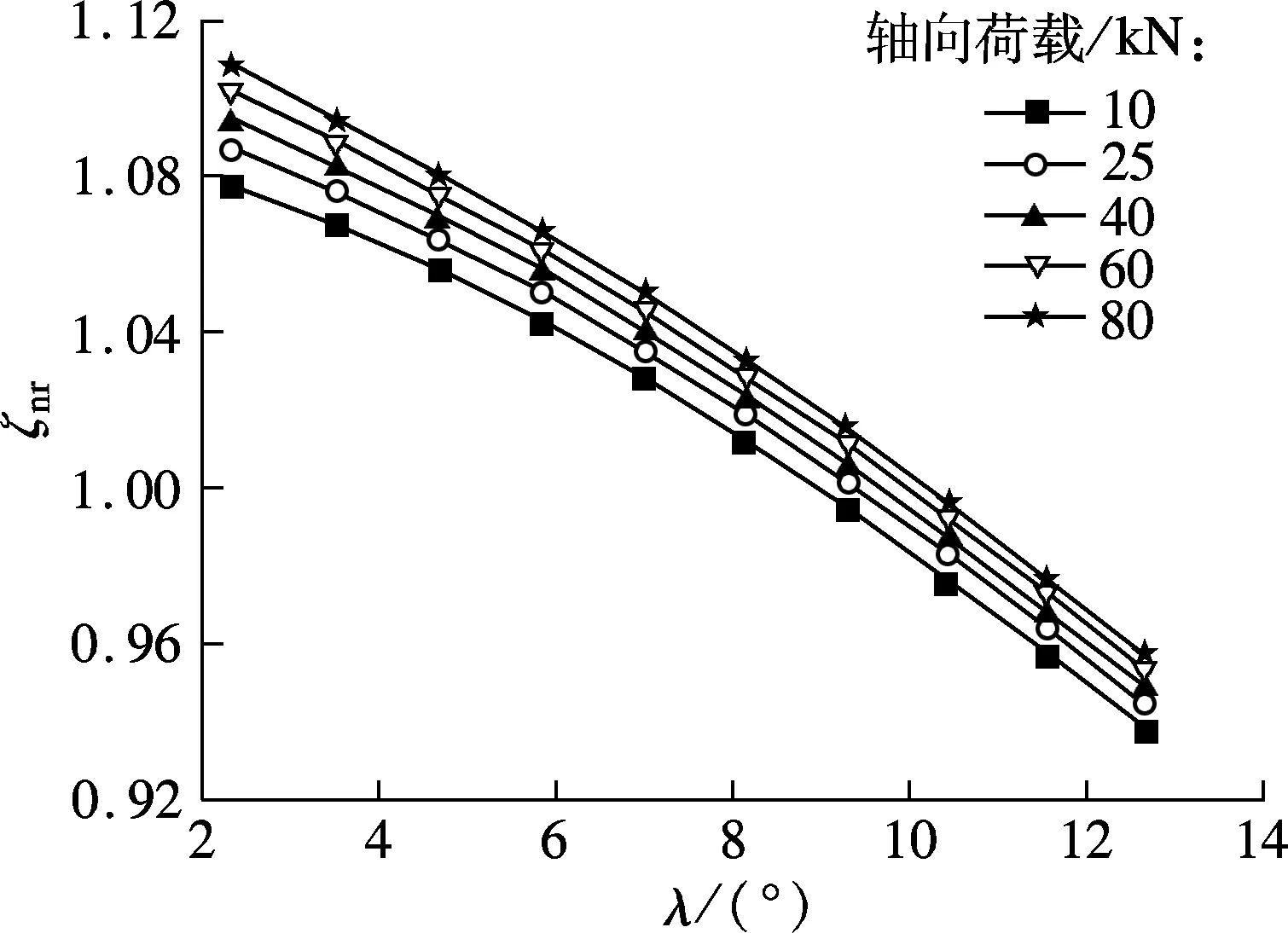
(b) 螺母

对比图4(a)和(b)可知,在相同轴向荷载下,随着螺旋升角的增加,两接触侧滑-滚比变化趋势相反.前者呈增大趋势,后者呈减小趋势.保持丝杠转速不变,丝杠螺旋升角越大,PRS的导程越大,这会导致滚柱自旋速度大幅增加,进而导致两接触侧相对滑动速度增大.但由于滚柱与螺母的螺旋升角相同且滚柱两端直齿与固联于螺母内部的内齿圈相啮合,在保证PRS可靠传动的同时,减小了滚柱与螺母接触侧的相对滑动[12].同时丝杠螺旋升角越大,螺母直线位移越大,相当于完成相同直线距离所产生的滑动量减小,这有助于提高PRS传动效率.在螺母侧,以80 kN为例,螺旋升角从2.337°增大到12.650°,滑-滚比下降了13.665 6%.可见,增大螺旋升角更有利于降低螺母侧滑动量,但丝杠和螺母均为多头螺纹,螺旋升角过大给螺旋滚道加工带来困难,难以保证螺纹精度,且螺旋升角决定了实际工况中的进给速度.因此,螺旋升角的设计可根据本文研究结果并结合实际使用和具体性能要求来确定.

2.3 滚柱螺纹牙数对滑-滚比的影响

滚柱螺纹牙数越多,PRS的承载能力和轴向刚度越大,但会导致轴向结构尺寸变大.为保证直线行程,丝杠必须加长,从而使得PRS轴向尺寸变大,故应合理地设计牙数,在保证承载能力和轴向刚度的同时,结构更加紧凑,节省安装空间.保持接触角为45°、螺旋升角为11.533°和丝杠转速为3 000 r/min不变,研究滚柱螺纹牙数在不同轴向荷载下对两接触侧滑-滚比的影响规律.计算结果如图5所示.

由图5可见,相同轴向荷载下,滚柱螺纹牙数对两接触侧滑-滚比的影响均较小,这是因为在相同轴向荷载下,滚柱螺纹牙数越多对荷载分布的影响越不明显[11],螺纹牙上的接触面积变化同样不明显.以本节参数为例,在轴向荷载为80 kN,滚柱螺纹牙数为10时,丝杠侧最大接触面积为1.156 4 mm2,螺母侧最大接触面积为1.376 2 mm2；滚柱螺纹牙数为50时,丝杠侧最大接触面积为1.015 1 mm2,螺母侧最大接触面积为1.208 2 mm2.因此,在保证PRS承载力和轴向刚度的前提下,应尽量减少滚柱螺纹牙数.在相同滚柱螺纹牙数下,随着轴向荷载增大,丝杠侧滑-滚比减小,螺母侧滑-滚比增大,其变化规律与接触角对两接触侧滑-滚比的影响相同.这是因为在丝杠侧,轴向荷载增大有利于增大作用在接触面上的法向力,增大丝杠侧接触力而减小相对滑动量. 对于螺母侧,同样能够增大接触力,但由于曲率半径较大,使得接触点坐标值较大,故在相同滚柱螺纹牙数下,随轴向荷载增大,滚柱螺纹牙数对两接触侧滑-滚比的影响规律相反.

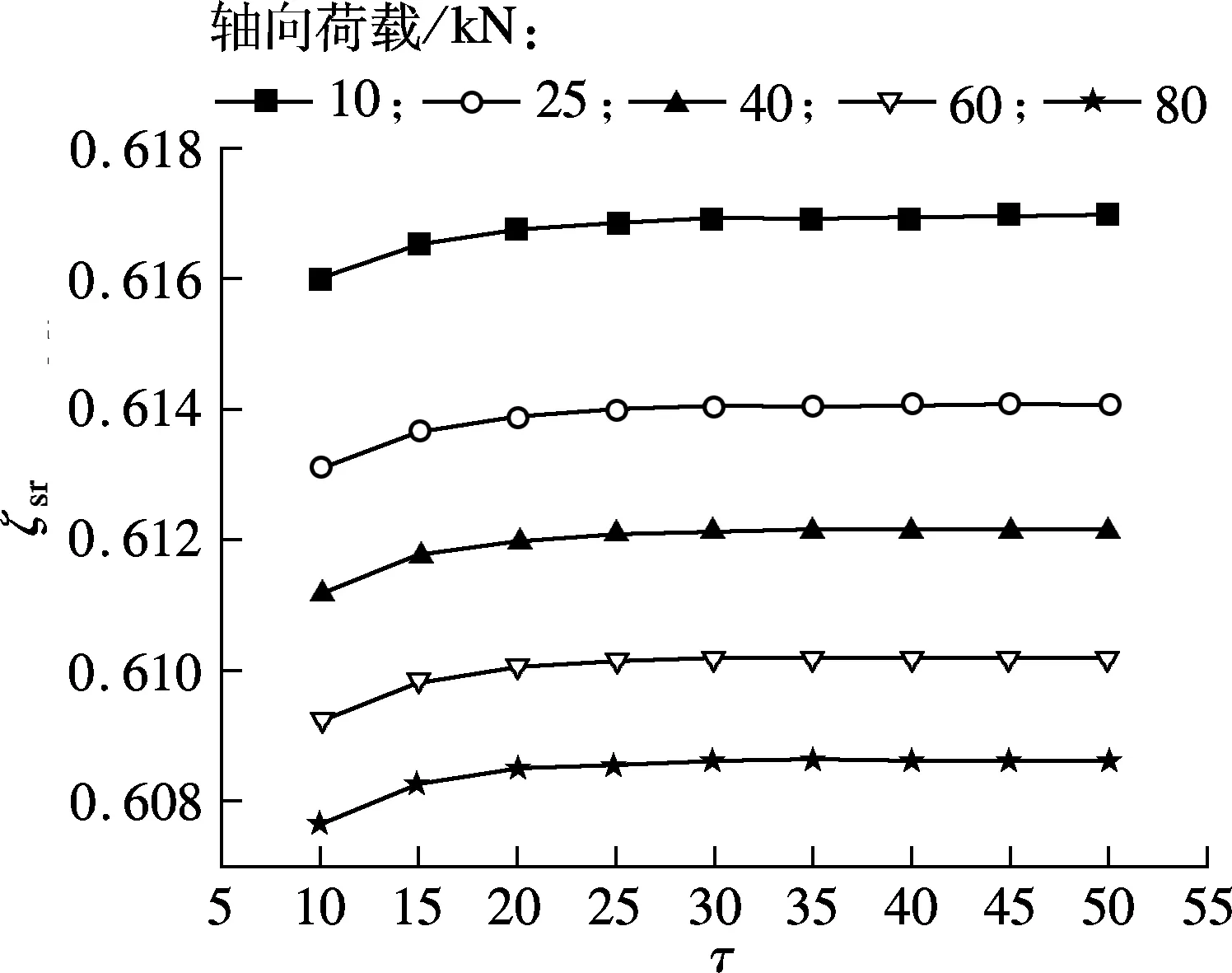
(a) 丝杠

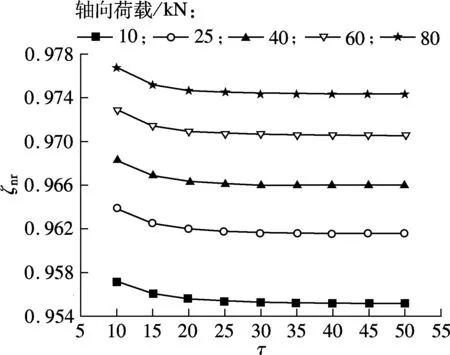
(b) 螺母

3 结论

1) 采用等效球的方法分别建立了PRS滚滑分析模型和考虑弹性变形的滚滑分析模型.采用滑-滚比表征两接触侧滑动量与滚动量的相对关系.

2) 丝杠侧在Frenet坐标系的3个方向均产生了相对滑动;考虑弹性变形,螺母侧仅有沿螺旋线切向和垂直于切平面方向产生的相对滑动,且两接触侧沿螺旋线切向产生的相对滑动速度最大.

3) 在相同轴向荷载下,随着接触角和螺旋升角的增大,两接触侧滑-滚比的变化趋势相反.增大螺旋升角更有利于降低螺母侧滑动量.

4) 滚柱螺纹牙数对两接触侧滑-滚比的影响均较小.因此,在保证PRS承载力和轴向刚度的前提下,可尽量减少滚柱螺纹牙数.

5) 本文参数对滑-滚比的影响规律具有普适性,研究结果可为PRS参数设计和深入研究其动态特性提供参考.

References)

[1]Rosero J A, Ortega J A, Aldabas E, et al. Moving towards a more electric aircraft [J].IEEEAerospaceandElectronicSystemsMagazine, 2007, 22(3): 3-9.

[2]Botten S L, Whitley C R, King A D. Flight control actuation technology for next-generation all-electric aircraft[J].TechnologyReviewJournal, 2000, 8(2): 55-68.

[3]Gong G, Drofenik U, Kolar J W. 12-Pulse rectifier for more electric aircraft applications [C]//ProceedingsoftheIEEEInternationalConferenceonIndustrialTechnology. Maribor, Slovenia, 2003, 2: 1096-1101.

[4]Bansal R C. Three-phase self-excited induction generators: an overview [J].IEEETransactionsonEnergyConversion, 2005, 20(2): 292-299.

[5]Todd R,Abdel-Hafez A A, Forsyth A J,et al. Single-phase controller design for a fault-tolerant permanent magnet generator [C]//ProceedingsoftheIEEEVehiclePowerandPropulsionConference. Harbin, China, 2008: 451-460.

[6]Claeyssen F, Jänker P, Leletty R, et al. New actuators for aircraft, space and military applications [C]//12thInternationalConferenceonNewActuators.Bremen, Germany, 2010: 324-330.

[7]Bennouna O, Langlois N. Modeling and simulation of electromechanical actuators for aircraft nacelles [C]//Proceedingsofthe9thInternationalSymposiumonMechatronicsanditsApplications. Amman, Jordan, 2013: 1-5.

[8]Brandenburg G, Brückl S, Dormann J, et al. Comparative investigation of rotary and linear motor feed drive systems for high precision machine tools [C]//Proceedingsofthe6thInternationalWorkshoponAdvancedMotionControl. Nagoya, Japan, 2000: 384-389.

[9]Ohashi Y, de Andrade A, Nosé Y. Hemolysis in an electromechanical driven pulsatile total artificial heart[J].ArtificialOrgans, 2003, 27(12): 1089-1093.

[10]靳谦忠, 杨家军, 孙健利. 行星式滚柱丝杠副的摩擦机理研究[J]. 华中理工大学学报, 1998, 26(6): 82-83,96. Jin Qianzhong, Yang Jiajun, Sun Jianli. The research on friction mechanism of the planetary roller screw [J].JournalofHuazhongUniversityofScienceandTechnology, 1998, 26(6): 82-83,96. (in Chinese)

[11]Ma S J, Liu G, Tong R T, et al. A new study on the parameter relationships of planetary roller screws [J].MathematicalProblemsinEngineering, 2012, 2012:340437-1-340437-29.

[12]Velinsky S A, Chu B, Lasky T A. Kinematics and efficiency analysis of the planetary roller screw mechanism [J].JournalofMechanicalDesign, 2009, 131(1): 011016-1-011016-8.

[13]Hojjat Y, Agheli M M. A comprehensive study on capabilities and limitations of roller-screw with emphasis on slip tendency[J].MechanismandMachineTheory, 2009, 44(10): 1887-1899.

[14]杨家军, 杨保哲, 朱继生, 等. 预紧力对行星滚柱丝杠轴向变形及摩擦的影响[J]. 机械传动, 2011, 35(12): 16-22. Yang Jiajun, Yang Baozhe, Zhu Jisheng, et al. Effect of preload on axial deformation and friction of planetary roller screw [J].JournalofMechanicalTransmission, 2011, 35(12): 16-22. (in Chinese)

[15]陈小芬, 李东波, 史翔. 滚子螺旋传动中滚子与丝杠之间相对滑动的机制研究[J]. 机床与液压, 2013, 41(9): 54-57. Chen Xiaofen, Li Dongbo, Shi Xiang. Mechanism research on relative sliding between roller and screw in roller screw transmission [J].MachineTool&Hydraulics, 2013, 41(9): 54-57. (in Chinese)

[16]Jones M H, Velinsky S A. Contact kinematics in the roller screw mechanism [J].JournalofMechanicalDesign, 2013, 135(5): 051003-1-051003-10.

[17]Wei C C, Lin J F. Kinematic analysis of the ball screw mechanism considering variable contact angles and elastic deformations [J].JournalofMechanicalDesign, 2003, 125(4): 717-733.

[18]马尚君, 刘更, 佟瑞庭. 行星滚柱丝杠副摩擦力矩及传动效率研究[J]. 哈尔滨工业大学学报, 2013, 45(11): 74-79. Ma Shangjun, Liu Geng, Tong Ruiting. The frictional moment and transmission efficiency of planetary roller screw [J].JournalofHarbinInstituteofTechnology, 2013, 45(11): 74-79. (in Chinese)

Rolling-sliding characteristics of planetary roller screw considering elastic deformation

Ma Shangjun Liu Geng Fu Xiaojun Tong Ruiting

(Shanxi Engineering Laboratory for Transmissions and Controls, Northwestern Polytechnical University, Xi’an 710072, China)

In order to disclose the rolling-sliding mechanism of the planetary roller screw, the models of rolling-sliding analysis of the planetary roller screw(PRS) with and without elastic deformation are developed by using the equivalent ball method based on the characteristic of spherical surface of the roller thread. The rolling-sliding characteristics are studied by calculating the relative slip velocities of contact points on the screw side and the nut side. The slide-roll ratios of two contact sides are calculated respectively to express the relative amounts of sliding and rolling. Furthermore, the influence of contact angle, helix angle and tooth number of the roller thread on slide-roll ratios is taken into account. The results show that the slide between the screw and the rollers always occurs considering elastic deformation and the relative slip velocity in the direction of tangent along helical trajectory on the screw side and the nut side is the highest. The influence trends of contact angle and helix angle on slide-roll ratios of two contact sides are opposite and the slide-roll ratio of the nut side can be reduced by increasing helix angle. Besides, increasing tooth number of the roller thread has little effect on the slide-roll ratios.

planetary roller screw; thread transmission; rolling friction; elastic deformation

10.3969/j.issn.1001-0505.2015.03.009

2014-09-12. 作者简介: 马尚君(1980—)，男，博士，助理研究员；刘更(联系人)，男，博士，教授，博士生导师, npulig@nwpu.edu.cn.

国家自然科学基金资助项目(51275423)、教育部高等学校博士学科点专项科研基金资助项目(20126102110019)、高等学校学科创新引智计划资助项目(B13044)、西北工业大学基础研究基金资助项目(3102015JCS05008).

马尚君，刘更,付晓军，等.考虑弹性变形的行星滚柱丝杠副滚滑特性[J].东南大学学报:自然科学版,2015,45(3):461-468.

10.3969/j.issn.1001-0505.2015.03.009

TH132.1

A

1001-0505(2015)03-0461-08