不同尺寸异径管的冲蚀数值模拟研究*

何兴建，李 翔，李 军

[1.中国特种设备检测研究院，北京 100013；2.中国石油大学(北京)，北京 102249]

异径管是石油化工装置管道中常用的连接配件，可起到改变管径调节介质流速、改变管道走向而管内介质流线都能顺畅,减少其压降和温降[1]，且可增加管道柔性减缓管道应力等多方面重要作用[2]，常用异径管的地方是泵的进出口、调节阀的进出口、温度计扩大管左右和再沸器进料分配管后[3]。现阶段异径管的设计与选用主要根据国内外标准进行[4-5]。在实际使用中由于异径管冲蚀穿孔、应力腐蚀、管件成形中在内壁面产生的沟痕等原始缺陷，以及边缘连接环缝区的开裂而导致的异径管失效事故时有发生[6-7]。冲蚀穿孔是异径管局部失效的主要原因之一。

近年来，国内外学者运用实验、理论、数值计算等方法对异径管冲蚀腐蚀磨损、流场以及应力等进行了部分研究，如偶国富等通过二维建模对异径管气液两相冲蚀磨损进行了研究，得出流体流向为“小进大出”时对腐蚀产物保护膜的影响要比“大进小出”小的多[8]；陈孙艺等对异径弯管的无力矩环向应力进行了计算分析，得出内压在异径弯管中引起的环向应力大小及分布与异径管大端圆面平均半径、小端圆面平均半径、壁厚、锥底角及经向弯角,管截面的圆周角有关[9]。但对尺寸与冲蚀情况之间关系的研究较少，为此作者通过对不同尺寸异径管进行冲蚀模拟研究，得出冲蚀情况与异径管尺寸之间的关系，以期为异径管的选取、制造及安全检测提供参考意见。

1 数学模型

1.1 数学模型建立

1.1.1 气相湍流模型

流场在异径管的变径区域变化比较大，为能较好的模拟变径区域的真实情况，采用适合流动类型比较广泛的RNGk-ε模型预测异径管的流场。并在商用软件Fluent流场模拟平台上进行数值模拟研究。

其方程如下。

(1)

(2)

式中：Gk是由于平均速度梯度引起的湍动能所产生；ρ是流体密度；Gb是由浮力引起的湍动能所产生；C1ε和C3ε是经验参数(分别取1.44和0.09)；YM指可压湍动能的膨胀对总耗散率的影响；σk是湍动能对应的普朗特数(默认值为1.0)；σε是湍动能耗散率所对应的普朗特数(默认值为1.3)。

1.1.2 气固两相流模型

设定异径管的最大入口含尘颗粒浓度为ρi(颗粒)=20 g/m3，对应的颗粒相的体积分率为ε=ci/ρp≪10%，模拟空间属稀相范畴，可以忽略颗粒之间的碰撞[10]，可以使用DPM模型。颗粒相的计算采用稳态藕合求解；用颗粒随机轨道模型计算颗粒轨道时，跟踪计算颗粒沿轨道的质量和动量的变化，将这些物理量引入到随后的气相流场计算中，既考虑气体对颗粒相的作用，又考虑颗粒对气体的作用，交替求解颗粒相与气相的控制方程，直到计算结果都达到收敛标准。

1.1.3 冲蚀模型

在模拟中所采用的DPM模型中冲蚀速率公式如下。

(3)

其中C(dp)为颗粒直径的函数，设定为一常数1.8×e-9，α为颗粒对壁面的冲击角，f(α)为冲击角的函数，v是颗粒相对壁面的速度，b(v)是此相对速度的函数，在模拟过程中速度指数函数为常数2.6。

1.2 边界条件与网格划分

1.2.1 几何结构

变径管的结构尺寸为入口管道直径取为D=100 mm，长度为1 000 mm，出口管直径取D=70 mm，长度取为800 mm，变径角度为θ=10°、20°、30°、45°、60°、70°、90°，坐标原点取在变径开始中心，具体尺寸见图1。

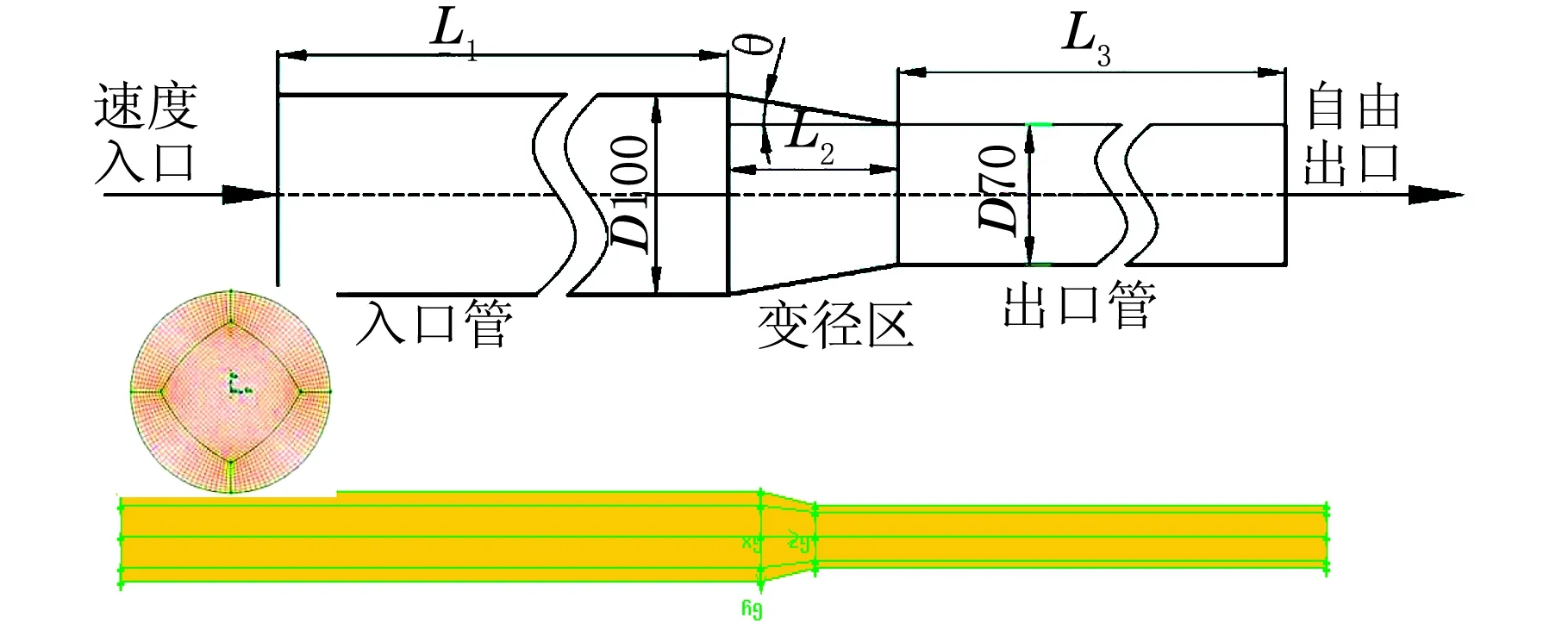
图1 异径管结构尺寸与横截面网格划分

1.2.2 入口边界条件

气相入口速度取v=10 m/s，入口ρ(颗粒)=1、5、10、15、20 g/m3。颗粒相入口边界条件为将颗粒入口处的射流源设为面源，颗粒均匀地分布在整个入口截面的网格上，由每一个网格中心射入，设定颗粒的入口速度与气相入口速度相同。计算过程中颗粒无质量变化，无热量传递，所以只设定颗粒密度和粒径。模拟粉料选用单一粒径煤粉，颗粒堆积密度为973.43 kg/m3，颗粒粒径为80 μm。

1.2.3 出口与壁面边界条件

气相出口边界条件按充分发展的管流条件处理，所有变量在出口截面处轴向梯度∂D/∂z为零。颗粒相出口边界条件为完全逃逸。气相流场在壁面采用无滑移边界条件，近壁网格采用标准壁面函数近似处理。颗粒对壁面的碰撞恢复系数取为完全反弹。

1.2.4 网格划分

气相流场选用SIMPLE算法求解。计算网格采用结构化网格，对应网格节点数分别为294 000～350 000个，横截面网格具体情况见图1。

2 结果与讨论

2.1 尺寸对冲蚀情况的影响

2.1.1 对冲蚀部位的影响

6种尺寸异径管在入口ρ(颗粒)=15 g/m3时的冲蚀严重位置图见图2。由图2可以看出随尺寸变化的规律为：在小角度时，冲蚀严重区域比较均匀，其形状为斑点状，分布在0.1～0.4 L之间壁面区域；随角度的上升，冲蚀区域(20°)向0.1～0.5 L之间扩展，严重区连成片状；随角度继续上升，严重冲蚀区域片状形状更加明显，严重区域集中在出口管与变径区域相连处，如在60°时，只在0.1～0.2 L之间且几乎连成环状,在90°时，严重冲蚀区域完全连成环状，其宽度为0.1～0.5 L。(注：严重冲蚀区域定义为最大冲蚀率的50%～100%)

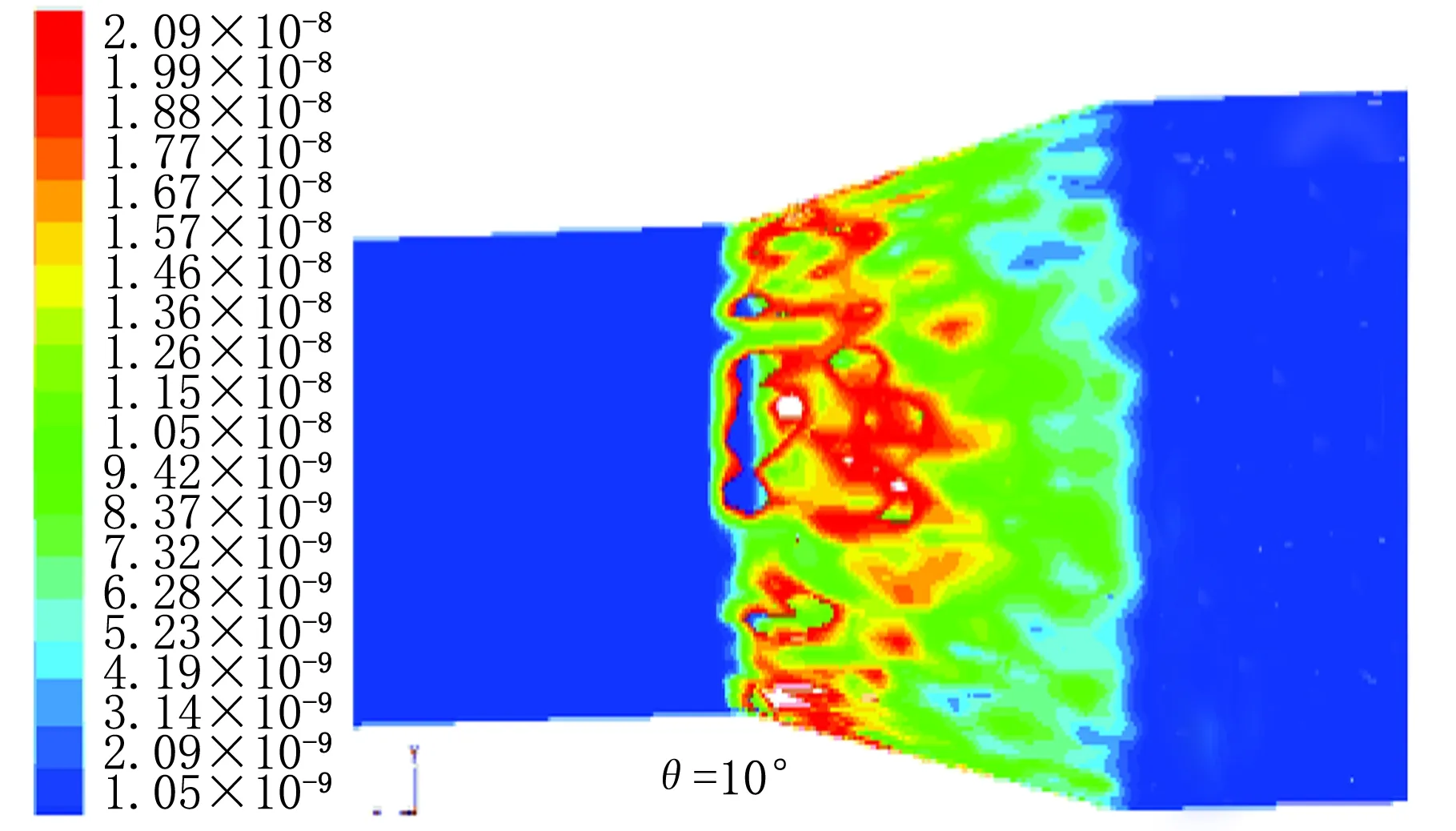
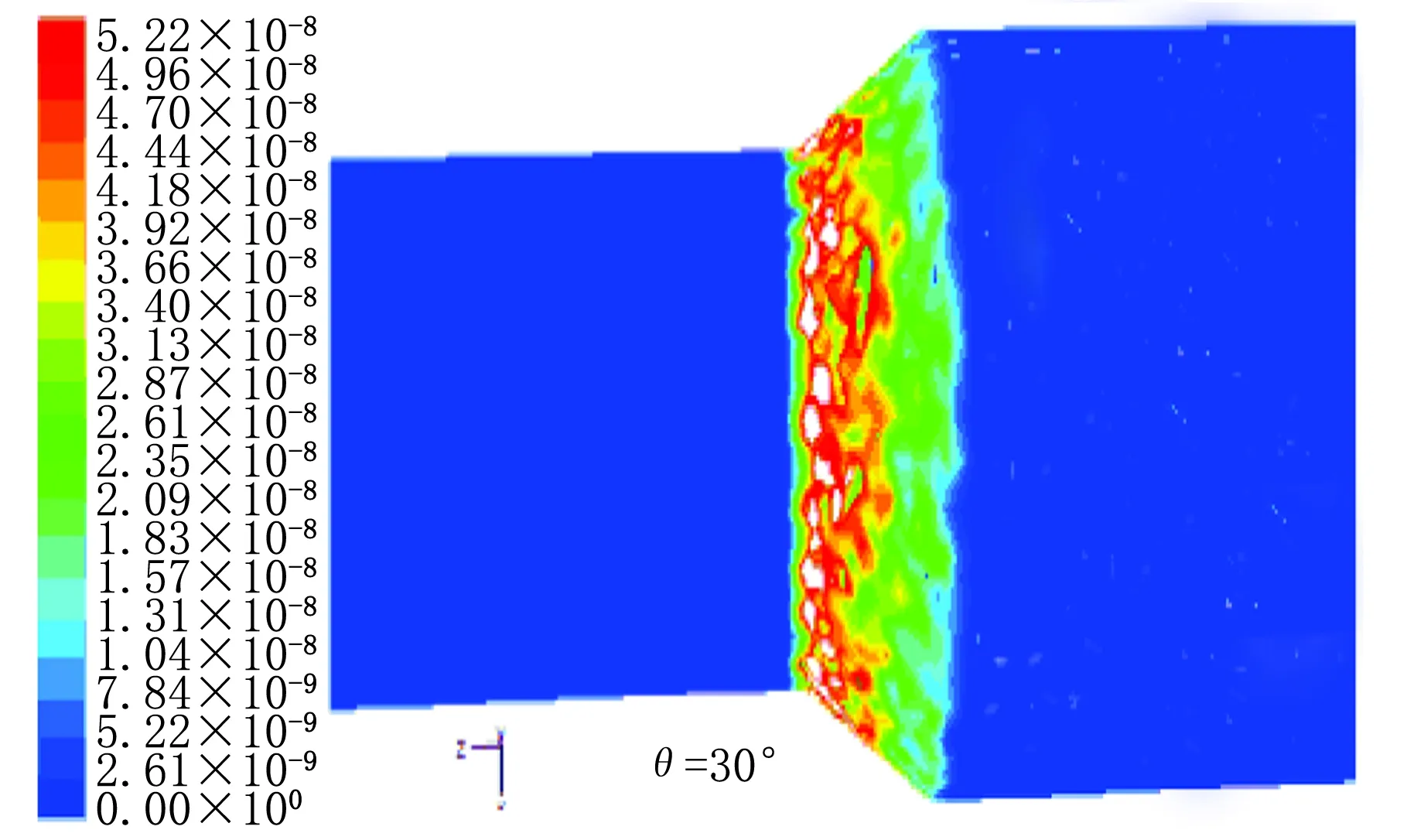
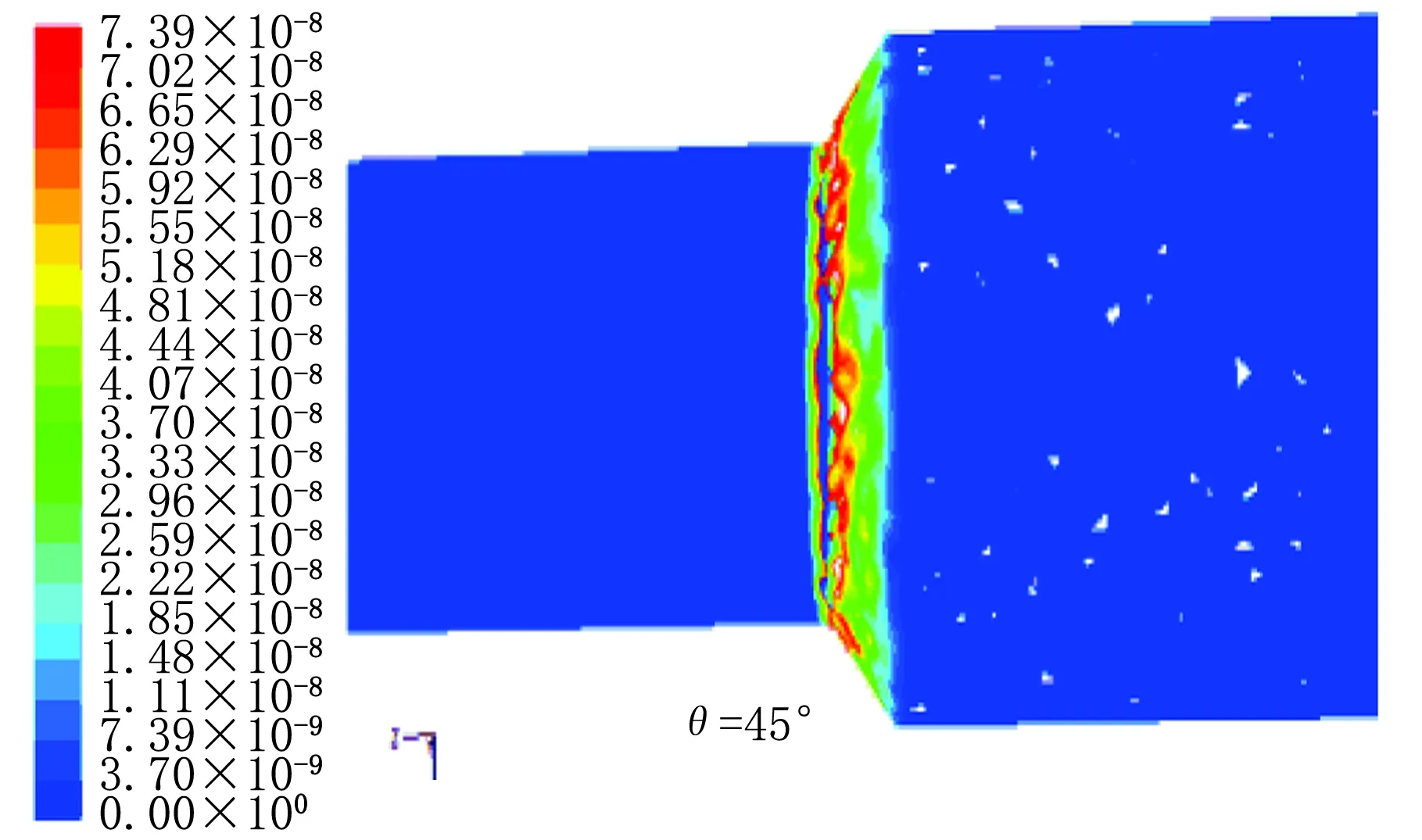
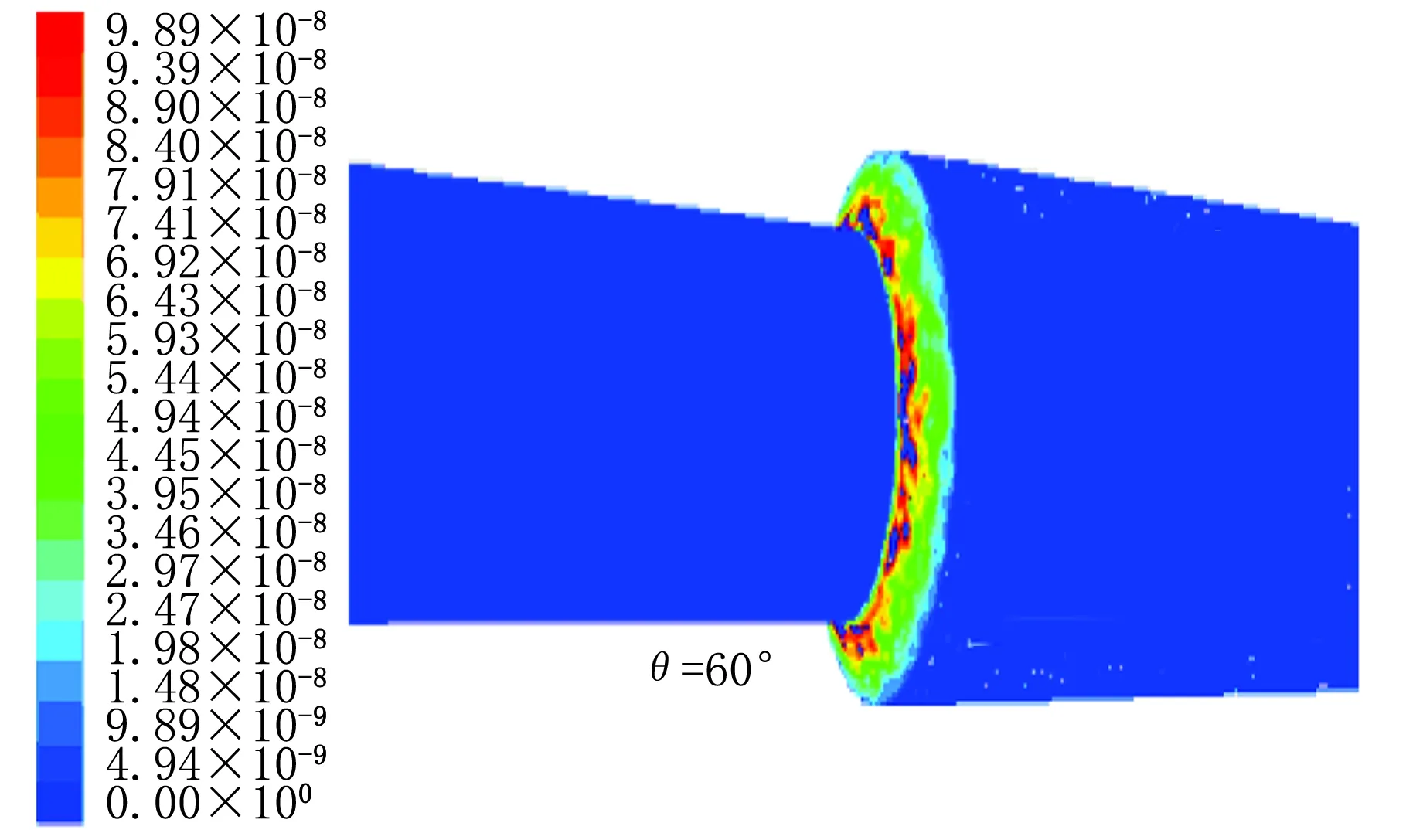
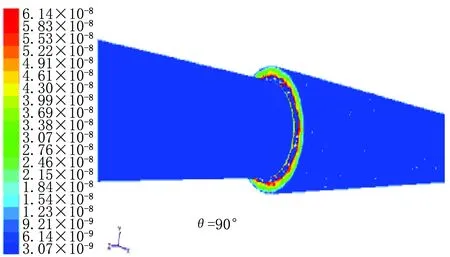
图2 冲蚀严重区域图[ρi(颗粒)=15 g/m3]

2.1.2 对冲蚀最大值的影响

对7种尺寸异径管的不同入口ρ(颗粒)进行对比研究，结果见图3。从图3中可知：在低浓度时(1 g/m3),异径管冲蚀率随角度上升而缓慢上升，不同尺寸异径管的冲蚀率相差不大；随着入口ρ(颗粒)上升，曲线有显著变化，入口ρ(颗粒)为 10 g/m3时，随着尺寸的变化，冲蚀率先快速上升，后在30°时上升幅度变缓慢，在70°之后冲蚀率开始下降，并在90°时冲蚀率下降为8×10-8kg/m2·s，小于70°时的1.13×10-7kg/m2·s，也小于45°时的8.75×10-8kg/m2·s,且随入口ρ(颗粒)的上升，此种趋势变得更加明显。这是因为颗粒撞击壁面角度随变径区域角度上升而增大，而壁面冲蚀严重程度随入射角度的上升的趋势为先上升后下降，并存在最严重的撞击角度[11]。同时入口ρ(颗粒)越大，差异累积越严重，故在入口ρ(颗粒)为20 g/m3时，曲线先上升后下降的趋势最明显。此外流场在变径区域转向，进而带动颗粒转向，导致颗粒与壁面的实际撞击角度并不是异径管的变径角度。

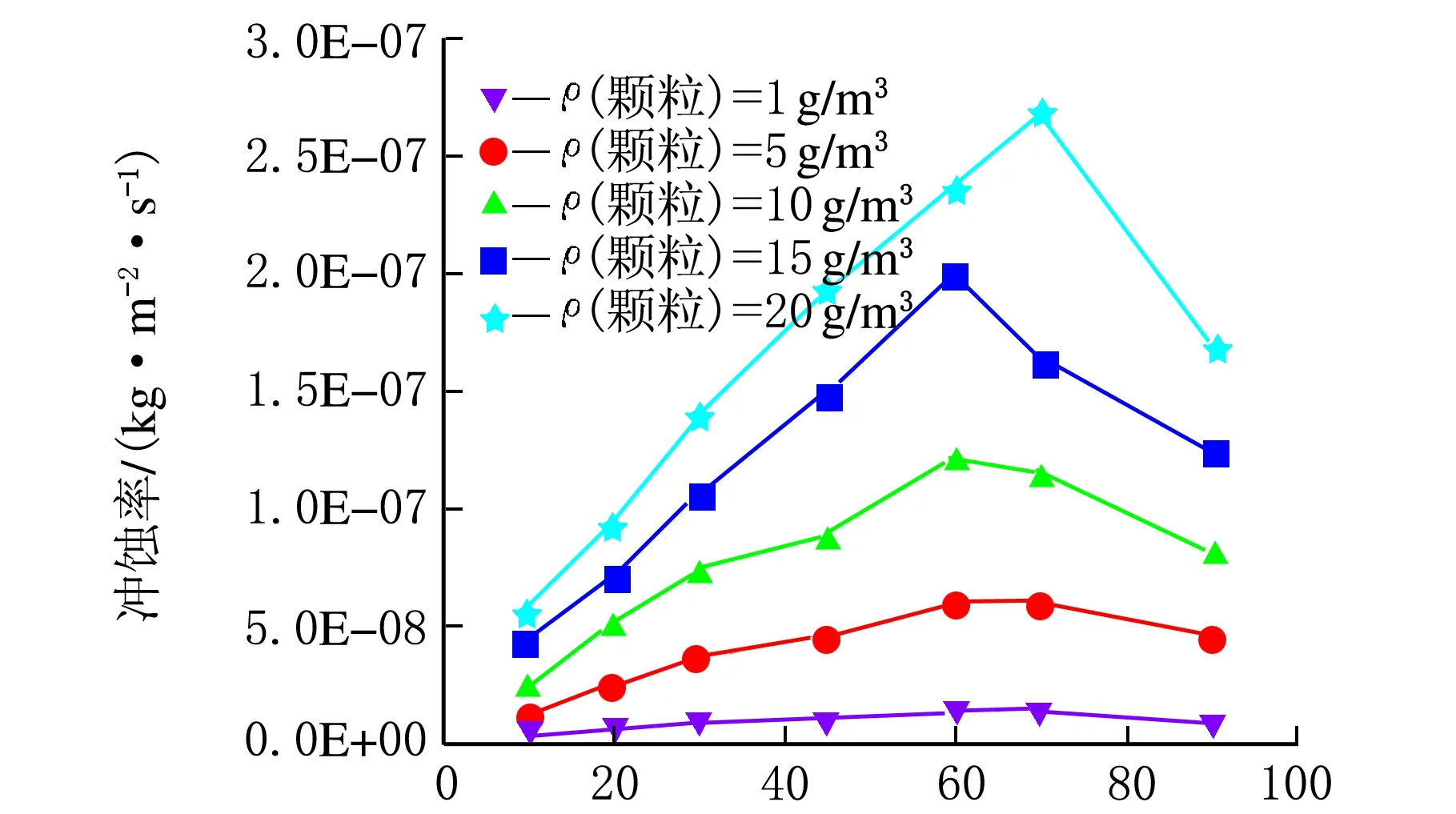
角度/(°)图3 冲蚀率随角度的变化(v=10 m/s)

2.2 入口ρ(颗粒)对不同尺寸异径管的冲蚀影响

为分析入口ρ(颗粒)与异径管冲蚀严重程度之间的关系，选定入口速度为10 m/s,ρ(颗粒)分别为1、5、10、15、20 g/m3，并对异径管冲蚀严重的部位进行取点研究，结果见图4。

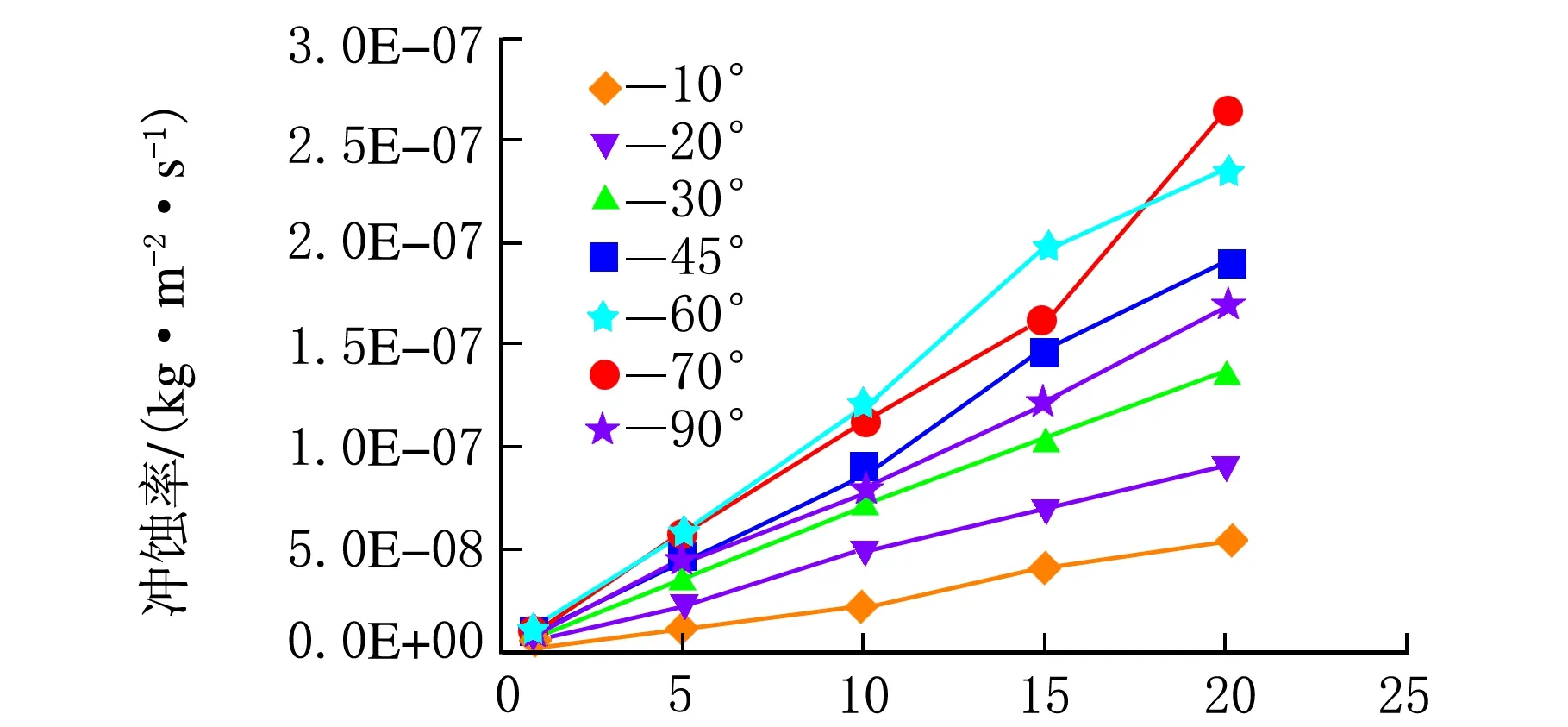
ρ(颗粒)/(g·m-3)图4 冲蚀率随入口浓度的变化(v=10 m/s)

由图4可以看出：冲蚀率随着入口ρ(颗粒)的上升而增加，在7种不同尺寸异径管中，冲蚀率的上升都呈现线性上升的趋势。这是因为在固定的入口速度下颗粒的能量以及与壁面碰撞的次数已经确定，ρ(颗粒)的上升只会增加入射颗粒的数量，颗粒数量只与冲蚀率成线性的关系，故出现冲蚀率随ρ(颗粒)增加而线性增长的现象。

此外在低浓度时，冲击严重程度主要由变径角度与颗粒数量来决定，可知存在一最严重冲蚀的变径角度。但随着ρ(颗粒)上升，加之在大角度时，颗粒在变径区域的ρ(颗粒)将进一步加大，ρ(颗粒)的增大导致流体湍动能增大，进而增大颗粒对壁面的撞击次数，出现70°尺寸异径管在高浓度20 g/m3时冲蚀率大于60°尺寸异径管的现象。

3 异径管使用、寿命及检测意见

实际工业中，在满足生产技术能力与工艺要求的前提下，应尽量使用小角度的异径管，以减小其严重冲蚀。在特殊情况下，需采用大角度的异径管时，应尽量避开最严重冲蚀变径角度。

此外在进行异径管的寿命评估时,主要根据异径管的冲蚀影响下凹坑的深度随时间的变化，并根据深度情况进行评估，故可以采用以下公式进行：

L深=k×E/ρ×n

其中：L深为冲蚀深度，m；E为冲蚀速率，kg/m2·s；ρ为异径管材料密度，kg/m3；n为异径管使用时间，s；k为由材料确定的待定系数。

对工业中某特定角度的异径管进行检测时，应重点对靠近出口侧的变径区域壁面进行检测；同时随ρ(颗粒)的上升，重点测量的范围应向入口侧延伸；必要时可先进行冲蚀模拟，预测冲蚀严重位置，为壁厚测量提供前期准备，再进行实际测量以期提高异径管检测的准确性。

4 结 论

(1) 异径管的冲蚀区域主要位于变径区域壁面，严重的冲蚀部位位于靠近出口的变径壁面。

(2) 异径管的严重冲蚀率随入口浓度的上升线性上升，随角度上升而呈现先增大后减小的趋势。且严重冲蚀区域的形状从小角度的斑点状向大角度的环状变化。

(3) 工业使用异径管时应避开最严重冲蚀变径角，在进行异径管的检测时，应对靠近出口侧的变径壁面加密测点。同时可减小入口ρ(颗粒)和加厚变径区域壁厚的方式减弱异径管变径区域的冲蚀破坏作用。此外根据作者研究得出的异径管冲蚀速率可以方便、快捷的预测出管道的寿命。

[ 参 考 文 献 ]

[1] 梁志正，等.重整加氢联合装置氛腐蚀及其防护措施[J].石油化工腐蚀与防护,1995,16(1):24-26.

[2] 陈孙艺，等.异径管三维实体模型的计算机建模方法[J].工程图学学报,2005(2)：137-141.

[3] 钟文学.谈谈配管设计的误区[J].化工设备与管道,2001(4)：33-35.

[4] 陈孙艺，等.异径管的标准及其失效分析[J].化工设备与管道,2005,6(45)： 25-28.

[5] 刘一民译.工厂制造的锻制钢对接焊管件[M].兰州：兰州石油机械研究所,1994：1.

[6] 栗雪勇.加氢裂化装置炼高含硫油后的腐蚀与防腐[C].//第五届压力容器使用管理学术会议论文集.南京：加工高含硫油设备和管道防腐蚀技术研讨会，2002：42.

[7] 沈中华.乙二醇装置六效蒸发系统腐蚀分析[J].扬子石油化工,1999,14(3):10-13.

[8] 偶国富，等.异径管冲蚀失效的流固耦合数值模拟[J].力学学报，2010，42(2)：197-204.

[9] 陈孙艺，等.异径弯管的无力矩环向应力解析解[J].压力容器,2007,24(2)：35-39.

[10] 朱红钧，等.Fluent12流体分析及工程仿真[M].北京:清华大学出版社,2011:41-42.

[11] Finnie I.The mechainism of erosion of ductile metals[M].Newyork:Proc,3Td US Nation,conf,on Appli,mesh,ASME,1958:527-532.