基于光干涉法的光学玻璃应力测量方法研究
郭长立,杨 曼,郭朝霞,王守全,杨 易
(西安科技大学 理学院,陕西 西安 710054)
基于光干涉法的光学玻璃应力测量方法研究
郭长立,杨 曼,郭朝霞,王守全,杨 易
(西安科技大学 理学院,陕西 西安 710054)
以平板理论为基础,利用牛顿环应力变形导致干涉图样的微小变化,提出一种基于光干涉法测量玻璃体应力的无损测量方法。理论推导出牛顿环曲率半径与应力之间的变换关系,利用自行设计的可安装在牛顿环仪上的施压装置,实验研究了施加应力与干涉图样的变换关系,通过理论分析与实验比较,证明了用牛顿环干涉法测量应力的可行性。利用该装置及方法对光学玻璃试样的应力进行测量,测量结果与实际施加的应力进行比较,误差最小为0.8%。
光干涉法;应力测量;平板理论;牛顿环;应力施加装置
引言
牛顿环是典型的等厚干涉装置,应用领域广泛,可用于测量透镜表面曲率半径、测量液体折射率、判断透镜表面凹凸、检测光学元件表面质量等[1]。在应用牛顿环测透镜曲率半径过程中,由于透镜和平板玻璃的接触面会受力变形,使二者不再是理想点接触,导致较大测量误差[2-3]。本文利用应力变形这一影响测量误差的因素,借助应力作用下牛顿环干涉图样的微小变化,以平板理论为基础,理论推导出牛顿环曲率半径与应力之间的变换关系,应用自行设计的可安装在牛顿环仪上的施压装置,探索研究一种基于光干涉法测量光学玻璃应力的无损测量方法。
1 平板理论及光学玻璃应力测量方法分析
牛顿环实验装置结构如图1所示,在一块水平的玻璃片B上,放一曲率半径R很大的平凸透镜A,上下2块玻璃用3个固定螺丝连接,用来调节A和B的相对位置,以改变牛顿环的形状和位置,同时上面的平凸透镜A将固定螺旋的张力传递到下面圆板玻璃B的中心[4]。通过受力分析可知,由于薄平凸透镜受平板玻璃的弹力和平板玻璃受透镜的压力,彼此均发生了形变,因而使干涉圆环中心由小黑点变成了圆形黑斑[5]。

图1 牛顿环实验装置结构示意图Fig.1 Structural diagram of Newton’s ring experimental device
依据平板理论[6]在侧向载荷下小挠度平板的基本方程,可将牛顿环中受力变形的光学玻璃看作一承受集中应力的小挠度薄板,结合圆板玻璃的边界条件和边缘简支的条件,若刚性圆板的半径为a,于圆心处承受一集中应力P,引起平板玻璃下凹,设平板的挠曲刚度为D,则半径r处平板的挠度可以表示为[7]
(1)
在圆板的边缘为简支的情况下,泊桑比为μ,则半径r处平板的挠度(形变)可以表示为
(2)
显然,按(2)式,平板玻璃中央(r=0)处的挠度最大,可以用下式给出:
(3)
如果平板玻璃没有变形,则半径为r处空气缝隙厚度e为
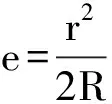
(4)
但现在平板玻璃有变形,半径为r处空气缝的厚度变为
h=e-(ωmax-ω)
(5)
代入暗纹公式:
(6)
并取级次分别为k和k+m,就可以推导出牛顿环所受应力p的逐差法公式:
(7)
2 牛顿环加压装置设计
目前市场上的加压装置受机械结构限制无法合理安装在牛顿环仪上,且容易对小型试样造成损害[8-9]。因此需要自行设计可以合理安装在牛顿环仪上的加压装置,满足实时显示或读取施加压力的大小,控制施加压力大小在玻璃弹性范围以内,能在压力范围内进行调节等要求。
自行设计的加压装置CAD机械图如图2所示,加压装置由变形牛顿环仪、外支撑架和砝码托盘3部分组成。变形牛顿环仪是在标准牛顿环仪的基础上扩大压盖与底盖的外径而成;外支撑架由尺寸相同的圆形上下端盖和圆杆组成,3个尺寸相同的圆杆连接外支撑架的上下端盖,外支撑架上端盖的中心设有与牛顿环仪底座直径相同的圆形凹槽;砝码托盘由圆杆与底部托盘连接而成,砝码托盘的圆杆穿过外支撑架的上端盖及变形牛顿环仪的上部压盖,并在圆杆顶端用螺母与压盖紧固连接。在砝码托盘上分别放置一定质量的砝码,砝码对牛顿环仪的拉力转化为对牛顿环仪压力,从而对牛顿环仪进行加压。根据文献[10]所述结构自制加压装置,如图3所示,外部尺寸为200mm×263mm,用亚克力板、工业尼龙和铝条制成。
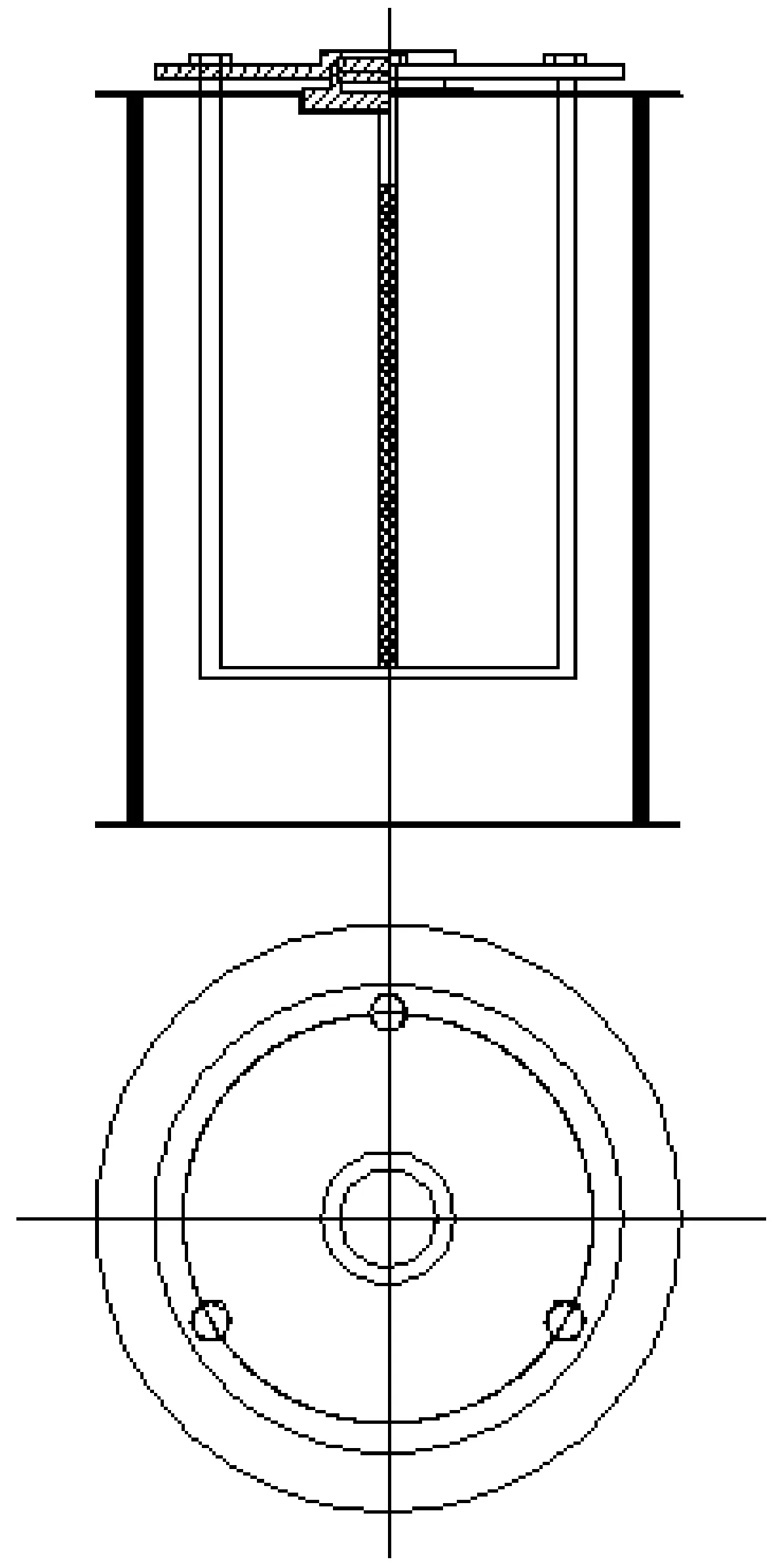
图2 加压装置机械图 Fig.2 Mechanical drawing of pressure device

图3 加压装置加工成品图 Fig.3 Finished product image of pressure device
3 光干涉法测量光学玻璃应力实验研究
光学玻璃应力测量实验的实验平台示意图如图4所示,由JCD3型读数显微镜、低压钠灯电源及JP20Na低压钠灯(波长为5.893×10-7m)、变形牛顿环仪及自行设计的应力施加装置组成。
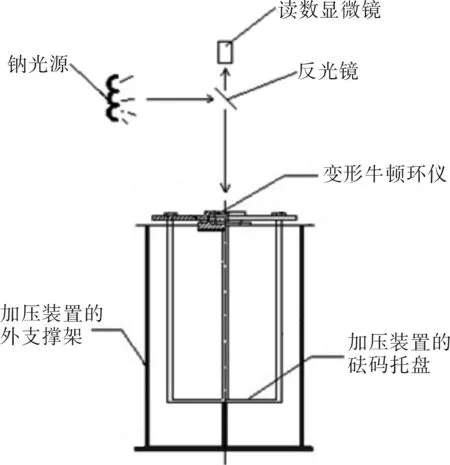
图4 光学玻璃应力测量实验平台示意图Fig.4 Diagram of experiment platform used for stress measurement of optical glass
3.1 不同应力下测透镜曲率半径
利用图4所示搭建的基于光干涉法测量光学玻璃应力的实验平台进行实验测量。在加压装置的砝码托盘上分别放置质量为0 kg,1 kg,2 kg,…,6 kg的U型砝码,将加压装置置于读数显微镜下,使变形牛顿环的中心正对着显微镜的物镜。当在加压装置的托盘上放置砝码时,上部凸型玻璃将砝码对托盘的张力传递到下部平板玻璃的中心,此时玻璃体受到的压力即为变形牛顿环仪上盖、平凸透镜、砝码托盘及砝码对平板玻璃的共同作用力,引起平板玻璃下凹变形,因此平板玻璃于圆心处承受的集中应力分别为0.102 N、6.972 N、16.766 N、26.560 N、36.355 N、46.149 N、55.944 N、65.738 N。分别读取干涉条纹中0~25级暗环直径的左右坐标,并计算此时透镜的曲率半径。
分析表1和表2中数据可知,在玻璃体受力时,平凸透镜的曲率半径值皆大于标准曲率半径(R=1 307.88 mm);随着砝码质量的增大,平板玻璃于圆心处承受的集中应力从0.102 N增加到65.738 N,而其对应的曲率半径从 1 308.63 mm增大到1 408.14 mm;随着砝码质量的增大,将对应的透镜曲率半径与标准曲率半径(R=1 307.88 mm)进行比较,相对误差从最小的0.1%增大到7.7%。
表1、表2中的数据用图形表示为图5,从图5所示可以直观地看出,随着平板玻璃于圆心处承受的集中应力P增大,与之对应的平凸透镜的曲率半径R不断增大。

表1 不同应力下透镜曲率半径结果比较1 mm
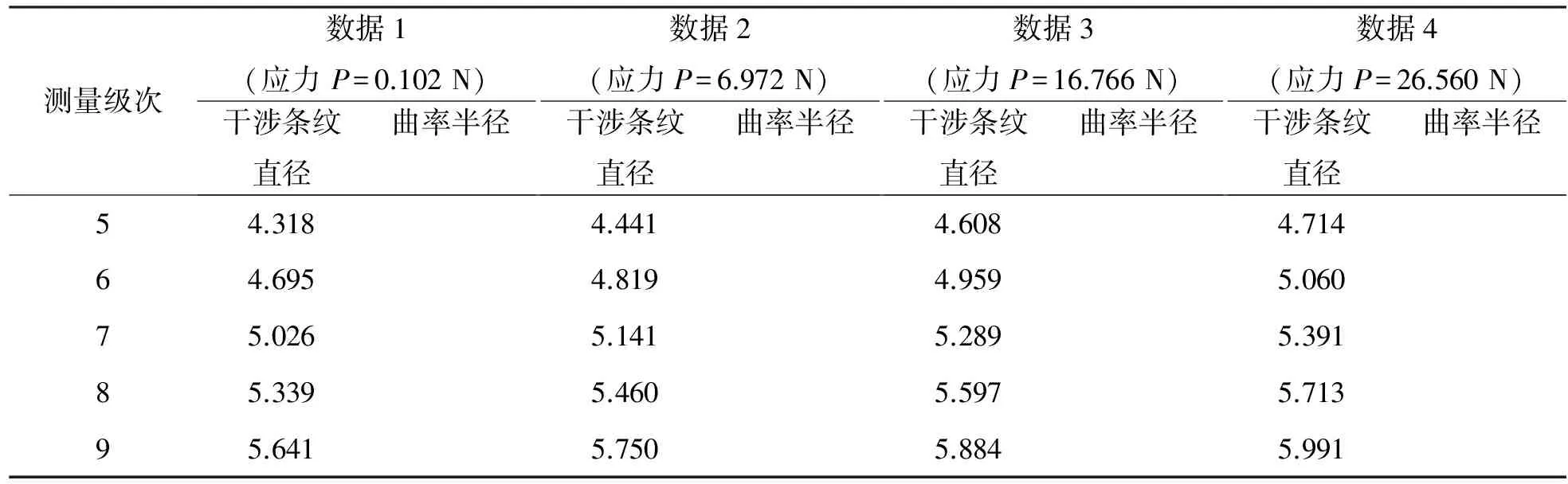
表2 不同应力下透镜曲率半径结果比较2 mm
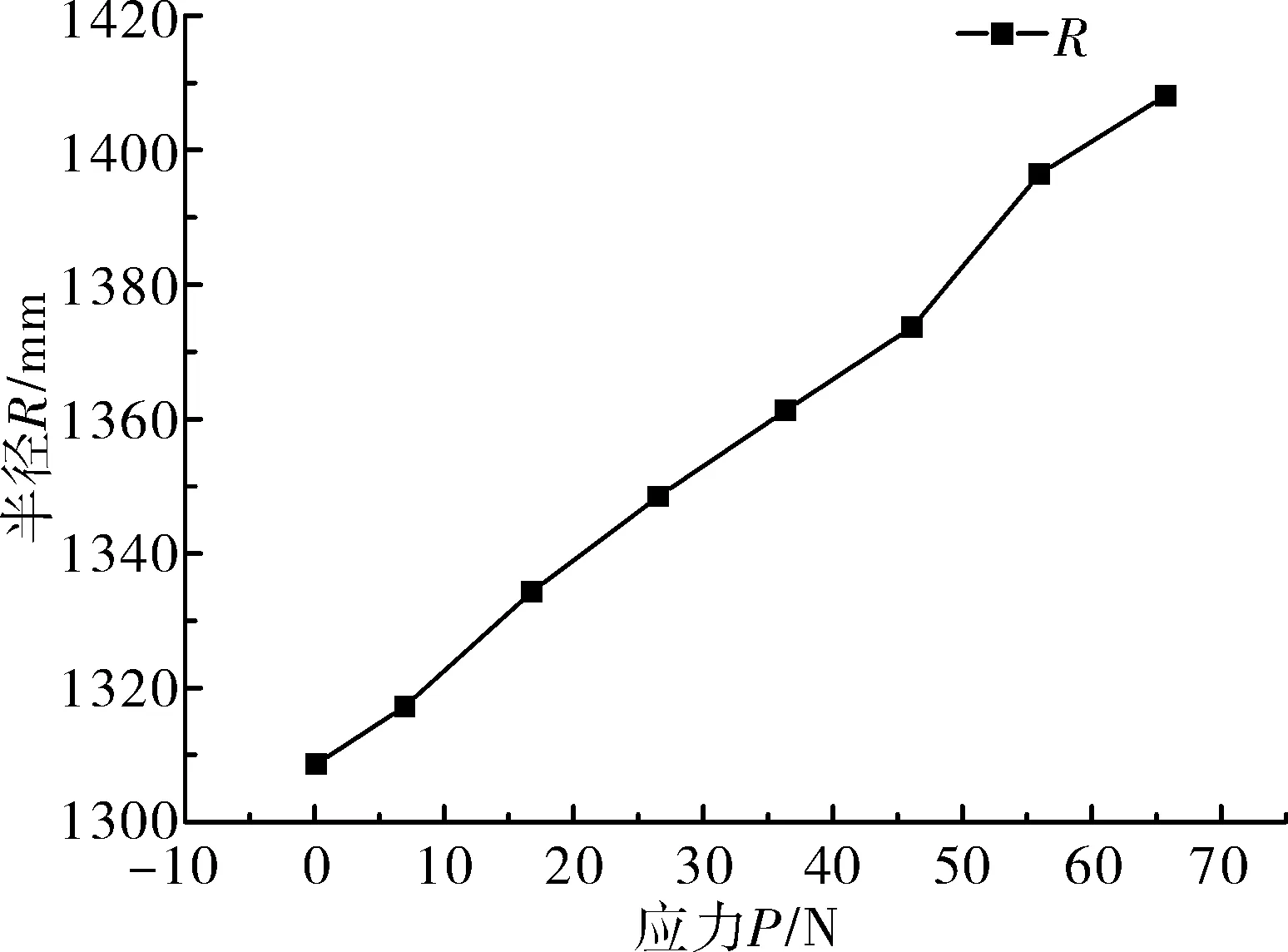
图5 应力P与曲率半径R对应曲线图Fig.5 Curvature radius R versus stress P
重复上述实验,选取10组典型实验数据,10组R-P对应关系如图6所示。由图6中的10条R-P折线可以看出,除了由系统误差造成的个别点突变外,10条R-P折线的变化规律整体表现为不断增长的趋势,即曲率半径R随着应力P的增大而增大。

图6 10组R-P对应关系图Fig.6 10 groups of R-P curves
10组R-P数据取平均值,绘制平均值P-R折线图,并对折线进行多项式拟合,拟合图形如图7所示。图7中的折线是应力与曲率半径对应关系曲线,可以看出玻璃体所受应力P的大小随平凸透镜曲率半径R的增大而增大,将数据点进行多项式拟合,拟合曲线如图7中的平滑曲线所示。
玻璃体受力与曲率半径变化的二项式拟合公式:
P=-3 123.562 95+3.913 83R-0.001 17R2
(8)
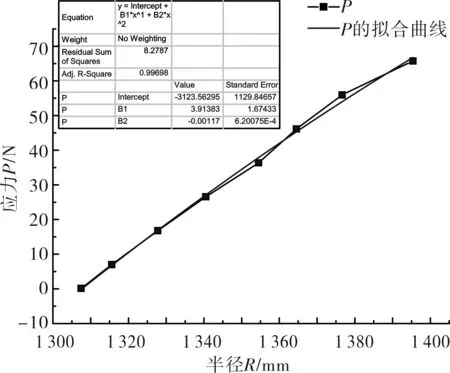
图7 P-R对应关系曲线及拟合曲线Fig.7 P-R curve and fitting curve
3.2 拟合公式验证
为了验证玻璃体所受应力与曲率半径的线性拟合公式的准确性,对玻璃体受力与曲率半径线性拟合公式进行验证实验。在应力施加装置的托盘上连续放置质量为1 kg,1.5 kg,2 kg,2.5 kg,…,6.5 kg的砝码,并分别测量透镜的曲率半径。将玻璃体上实际施加的应力与线性拟合公式计算得出的应力进行对比验证,数据结果如表3所示。
由如表3可见,除个别点由于试验过程中系统误差导致相对误差达到18%以外,其余由玻璃体应力拟合公式计算得出相对误差都在10%以下,最小相对误差为3.0%,线性拟合公式计算得出的应力与实际施加的应力较为接近,可以验证玻璃体应力拟合公式的准确性。因此可以得出结论,平凸透镜曲率半径R随着玻璃体所受应力P的增大而增大,玻璃体所受应力的大小P与在其应力作用下透镜曲率半径R具有规律性的对应关系,其对应关系可由璃体应力拟合公式P=-3 123.562 95+3.913 83R-0.001 17R2表示。
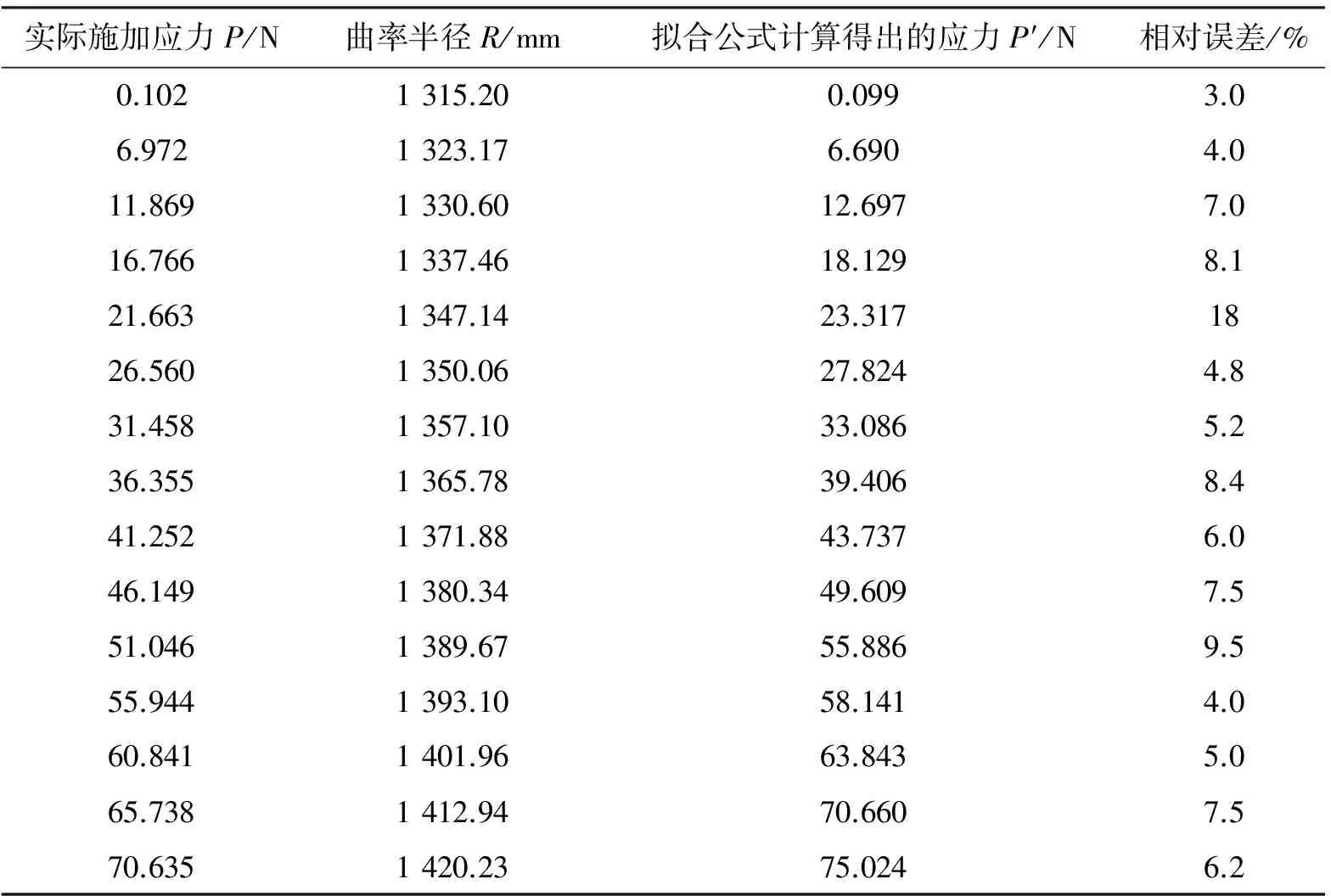
表3 拟合公式计算得出的应力P′与实际施加的应力P的比较
3.3 理论公式验证
为了验证利用平板理论推导出的玻璃体应力理论公式的准确性,应用自行设计的加压装置和玻璃体应力试验平台对玻璃体应力理论公式进行实验验证。在应力施加装置的托盘上连续放置质量为0 kg,0.2 kg,0.4 kg,…,6 kg的砝码,测量出对应牛顿环干涉条纹各级暗环直径,并对得出的数据进行数据处理,代入玻璃体应力理论公式(7),则有:
将通过公式计算得出应力值与实际施加应力进行比较,数据结果如表4所示。
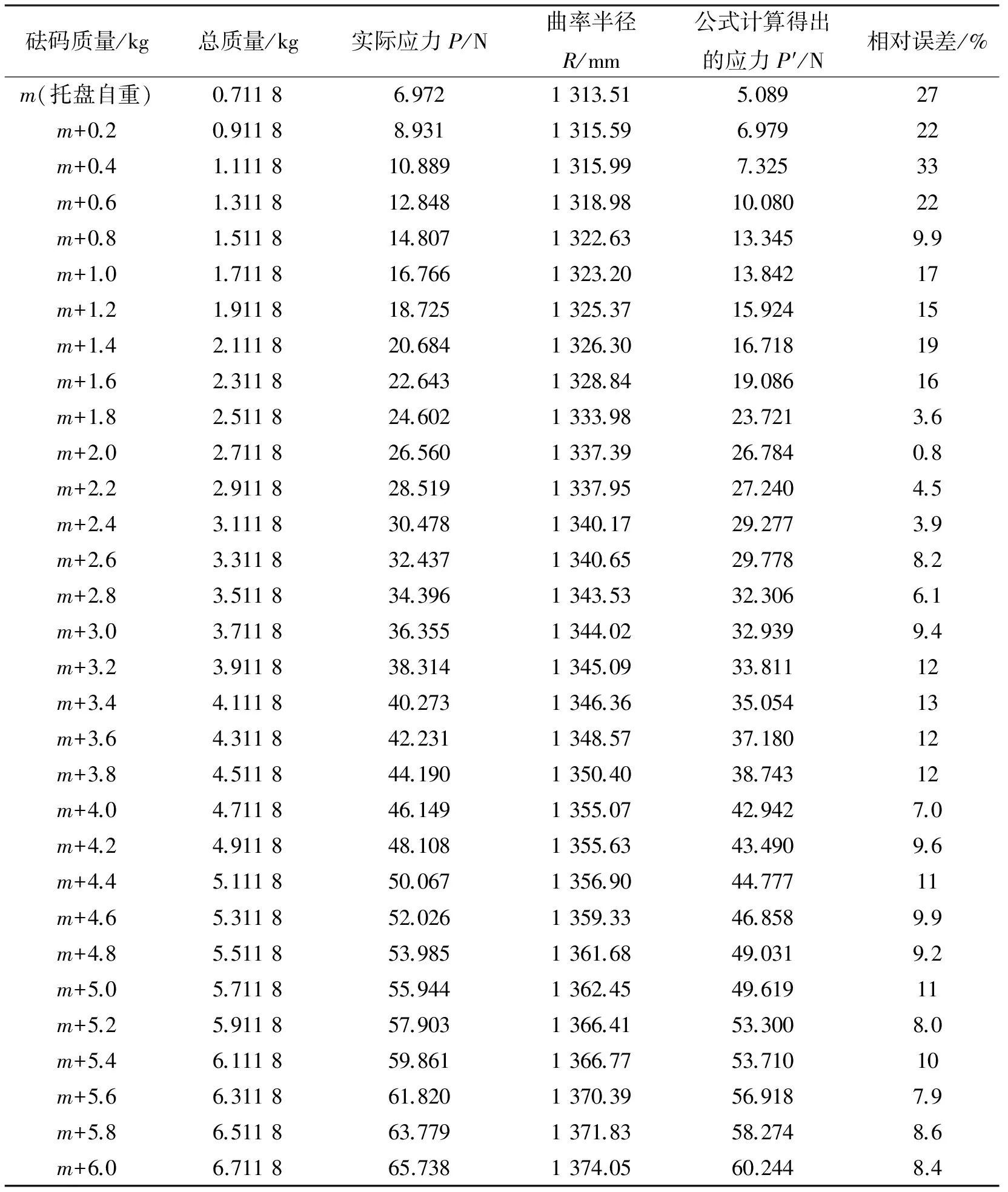
表4 应力的理论值与实际值之比较
如表4所示,将理论公式计算得出的应力与实际施加的应力进行验证比较,可知在放置砝码质量为0~0.6 kg之间时,由于玻璃体所受应力较小,牛顿环干涉条纹对应力反映不敏感,所以在微小应力区间内误差较大;随着放置砝码质量的增加,理论公式计算得出的应力与实际施加的应力的相对误差不断减小,在放置放码质量为0.8 kg~1.6 kg之间时,最小相对误差为9.9%,最大相对误差为19%;在放置砝码质量为1.8 kg~3.0 kg区间范围内,相对误差均在10%以下,最小相对误差达到了0.8%,说明此时理论公式计算得出的应力与实际施加的应力最为接近,测量效果最好;在放置砝码质量为3.2 kg~3.8 kg区间范围内,相对误差都在12%~13%之间;在放置砝码质量为4.0 kg~6.0 kg区间范围内,相对误差均在10%左右,说明这一区间内的理论公式计算得出的应力与实际施加的应力也较为接近,测量结果较好。
从图8可以看出理论公式计算得出的应力P′曲线与实际施加的应力P曲线变化规律相同,曲线较为接近,尤其在放置砝码质量为1.8 kg~3.0 kg范围内相对误差均在10%以下,最小达到0.8%,曲线基本重合,因此可以证明上文推导出的光学玻璃应力P理论公式的准确性。
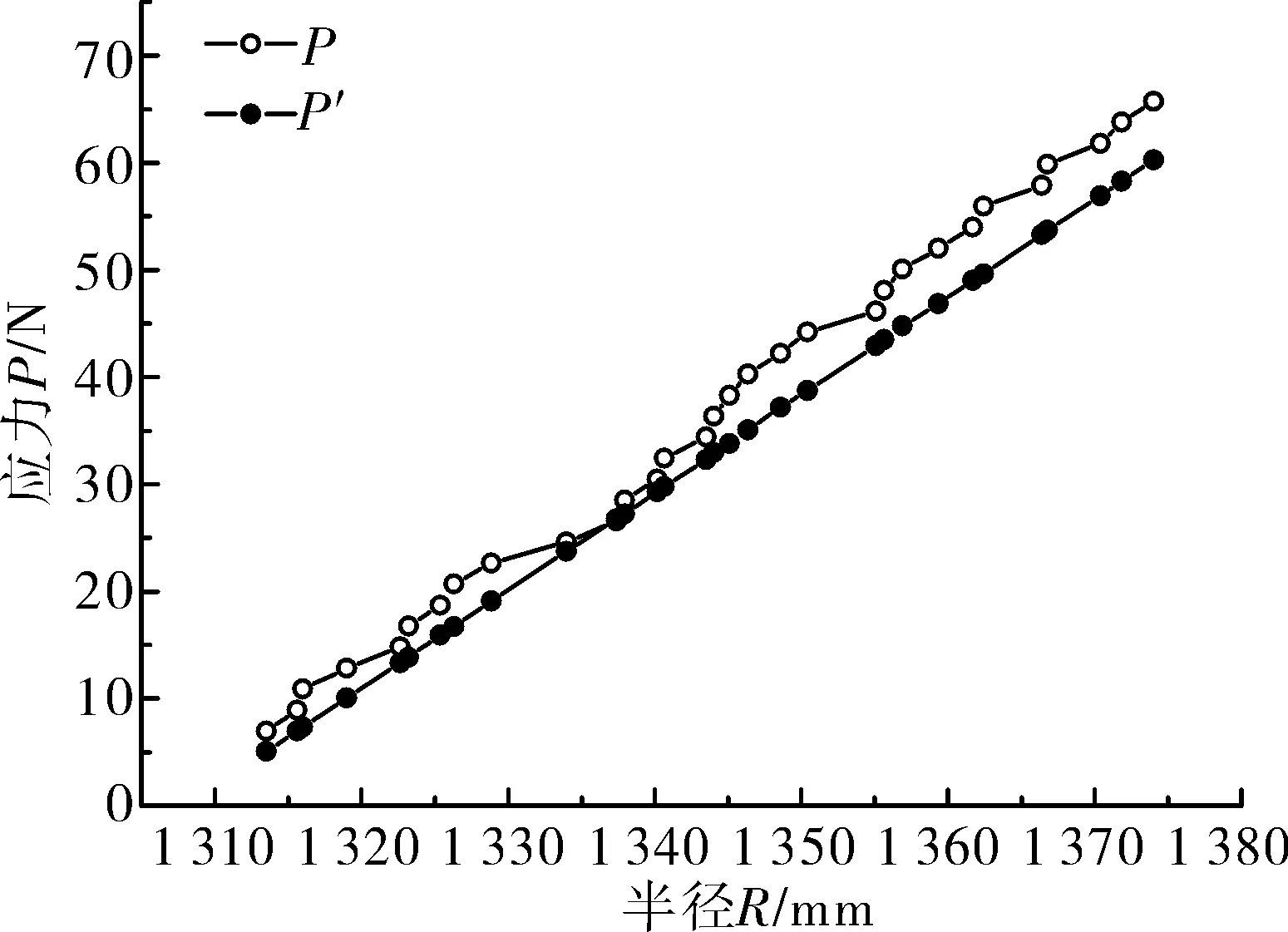
图8 公式计算的应力P′与实际应力P的比较图 Fig.8 Comparison diagram between calculated stress P′ and actual stress P
4 结论
本文探索研究了一种基于光干涉法测量光学玻璃应力的测量方法,理论推导了用牛顿环干涉法测量光学玻璃应力的解析公式,实验研究了光学玻璃应力与牛顿环曲率半径之间的对应关系。理论分析和实验研究表明:用牛顿环干涉法测量光学玻璃应力的方法是可行的,应力在2.511 8 N~3.711 8 N区间内的测量误差最小。
[1] Zhang Lijun, Zhang Yi, Bai Tingzhu. Research on a system and method of automated whole-field measurement of optical glass stress[J]. SPIE,2008,6834:401-409.
[2] Guo Changli.Analysis and application of laser Newton ring[J].Research and Exploration in Laboratory, 2011,30(6):18-20. 郭长立. 激光牛顿环现象分析及应用[J].实验室研究与探索,2011,30(6):18-20.
[3] Zhang Yong. Investigation of center of Newton’s rings[J]. Time Education,2014(23):193.
张勇. 牛顿环实验的环心探讨[J]. 时代教育,2014(23):193.
[4] Guo Changli. Physics experiment[M]. Xi’an: Northwest Polytechnical University Press,2009. 郭长立. 大学物理实验教程[M]. 西安:西北工业大学出版社,2009.
[5] Shen Zhirong, Liu Jianke.A new method of measuring bulk modulus of glass[J].Journal of Northwest Institute of Light Industry,1999,17(1):111-113. 申志荣, 刘建科. 测定玻璃体弹性模量的一种新方法[J]. 西北轻工业学院学报,1999,17(1):111-113.
[6] Yang Yaoqian. Plate theory[M]. Beijing: China Railway Publishing House,1980. 杨耀乾.平板理论[M].北京:中国铁道出版社,1980.
[7] Zhang Yongan, Qian Xiaofan, Zeng Chunping. The rectification of data processing form Journal of formula in Newton’s rings experiment[J]. Kunming Metallurgy College,2004,20(1):38-42. 张永安,钱晓凡,曾春平.牛顿环实验数据处理公式的修正[J]. 昆明冶金高等专科学校学报,2004, 20(1):38-42.
[8] Wang Cailing, Kang Renke, Jin Zhuji.Research and design on a device to apply down-force in chemical mechanical polishing process[J]. China Mechanical Engineering, 2010,21(7):839-864. 王彩铃,康仁科, 金洙吉.一种用于化学机械抛光的加压装置设计研究[J]. 中国机械工程, 2010,21(7):839-864.
[9] Tsai C H,Tien K C, Chen Mingche,et al.Characterizing coherence lengths of organic light-emitting devices using Newton’s rings apparatus[J]. Organic Electronics, 2010,11(3):439-444.
[10]Guo Changli, Yang Man, Guo Zhaoxia, et al. A stress measurement device of glass based on optical interference: Chinese,ZL201420664379.1[P]. 2015-02-11. 郭长立, 杨曼, 郭朝霞.一种基于光干涉法测玻璃体应力的测量装置:中国,ZL201420664379.1[P].2015-02-11.
Measurement method of optical glass stress based on optical interference
Guo Changli,Yang Man,Guo Zhaoxia,Wang Shouquan,Yang Yi
(College of Sciences,Xi ’an University of Science and Technology,Xi’an 710054,China)
Based on the plate theory, using the tiny changes of interference pattern under the stress deformation on Newton’s rings, we put forward an nondestructive optical vitreous stress measurement method based on the optical interference theory.We theoretically deduced the analytic formula between the curvature radius of Newton’s rings and the stress,by using a designed pressure applying device which could be reasonably installed on the Newton’s ring device, experimentally studied the transformation relation between the applied stress and the interference pattern, eventually proved the feasibility of the stress measurement method based on interference technique with Newton’ s ring through theoretical analysis and experimental comparison.Using this system to measure the stress of the optical glass sample, the minimum error between the measurement results and the actual stress is 0.8%.
optical interference; stress measurement; theory of plates; Newton’s rings; stress applying device
1002-2082(2015)06-0923-08
2015-06-23;
2015-08-30
教育部2014年立项课题(DWJZW201417xb)
郭长立(1966-),男,河南许昌人,教授,工学硕士,主要从事物理学教学、实验及应用研究工作。
E-mail:guocl@xust.edu.cn
TN206;TQ171
A
10.5768/JAO201536.0603005

