一种四波长轮换的表面形貌干涉测量系统
杨练根,余再新,何 浪,王选择,2
(1.湖北工业大学 机械工程学院,湖北 武汉 430068;2.天津大学 精密测试技术及仪器国家重点实验室,天津 300072)
一种四波长轮换的表面形貌干涉测量系统
杨练根1,余再新1,何 浪1,王选择1,2
(1.湖北工业大学 机械工程学院,湖北 武汉 430068;2.天津大学 精密测试技术及仪器国家重点实验室,天津 300072)
针对相移干涉法测量表面三维形貌时深度测量范围受波长限制这一问题,提出一种四波长表面形貌干涉测量系统。通过滤波片的轮换,将白光LED光源的光切换出4个不同波长的光源,并依次进行单波长干涉。为解决多波长干涉图像数据处理,采用基于椭圆拟合的算法,在逐帧逐点的相位计算条件下,运用大小尺度相结合的算法实现高精度宽范围的表面形貌测量。实验结果表明:在深度测量范围扩大到约41倍的条件下,测量经中国计量科学研究院采用粗糙度国家基准校准的方波多刻线样板,得到的表面粗糙度数据与校准数据相比,相对误差为4.09%。说明在一定的深度范围内,该系统能够实现表面形貌的高精度测量。
相移干涉; 表面形貌测量;四波长;相差;椭圆拟合
引言
基于光学干涉显微原理的测量是一种十分重要的微观表面形貌测量方法,具有快速、非接触、高精度的优点[1]。其中基于直接表面显微干涉的测量技术主要包括白光相移干涉、波长扫描干涉、双波长或多波长干涉等几种测量方法。白光相移干涉测量[2-3]以白光为光源,它通过相移驱动扫描,逐个寻找被测点的零光程差位置,实现表面形貌的高精度测量。这种方法的干涉条纹具有较好的对比度,但零级条纹位置点的识别精度[4-5]受到采样步距和光源频带宽度的影响,使之难以达到很高的测量精度。波长扫描干涉[6-7]通过AOTF连续改变干涉波长,因此在绝对光程差不变的情况下改变相对相位差,实现了超越2π范围内求相位变化与波长变化之比(即光程差)。该方法不需要驱动装置,并且理论上不受测量范围限制。双波长或多波长干涉测量方法的实质[8]是利用双波长或多波长测量结果的差异求出干涉级次,从而得到被测点的真实高度。虽然它拓展了深度测量范围,但同时也增大了相位识别误差[9],测量结果精度较低。目前,基于该方法测量形貌主要是依据小数重合技术[10],它对相位的识别精度要求很高,容易出现干涉级次判断的失误,导致测量失效。为了在扩大深度测量范围的同时,保证具有较高的相位识别精度,本文提出一种基于波长轮换与相移扫描相结合的表面形貌测量系统,以白光干涉的特性为基础,利用切换滤光片实现多波长的单色光光源照射,采用Mirau相移干涉[11]来获得被测表面的三维形貌。在干涉图像数据处理中采用椭圆拟合的算法,在逐帧逐点的相位计算条件下,运用大小尺度相结合的算法,实现表面形貌的高精度测量。
1 四波长干涉测量系统
测量系统结构示意图如图1所示,系统由光源轮换子系统、显微干涉测量子系统、图像采集子系统、PZT驱动子系统、二维工作台组成,整体由计算机控制。采用LED白光光源,4个不同波长的滤光片均匀分布在定制的圆盘上,步进电机驱动圆盘转动实现四波长轮换;显微干涉测量子系统采用Mirau干涉结构;图像采集子系统由高速CCD及图像采集卡组成;PZT采用开环控制[12];二维工作台采用光栅进行位移计量。
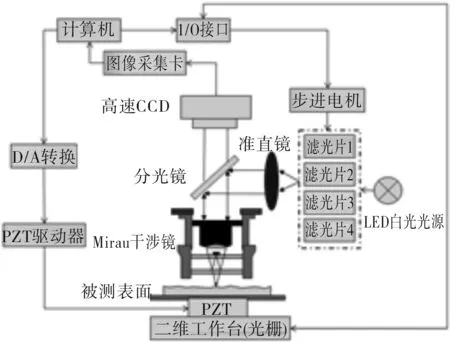
图1 测量系统示意图Fig.1 Diagram of measurement system
测量时,通过计算机输出信号控制步进电机驱动放置有4个滤光片的圆盘转动,LED白光光源发出的光经准直镜准直后的平行光分别通过4个滤光片,切换出4个不同波长的光源。同时计算机输出信号控制PZT和二维工作台驱动被测工件,完成半个波长以上的位移驱动,干涉条纹移动一个周期以上,PZT每一次位移都可以获得一幅干涉图像,高速CCD同步采集该波长下的干涉图。CCD同步采集到的4个不同波长下的干涉图分别存储在计算机中,通过对干涉图进行处理,恢复被测表面的表面形貌。
2 四波长干涉图数据处理原理
测量时,采用带宽为5 nm的4个滤光片。综合考虑相干长度受滤光片带宽限制及干涉条纹级次的识别受测量信噪比的影响因素,选用中心波长分别为510 nm、520 nm、550 nm、640 nm的4个滤光片。
步进电机驱动安装有滤光片的圆盘实现波长轮换。计算机控制PZT及二维工作台移动,PZT每移动一次都可以获得一幅干涉图,PZT等步距驱动40次,CCD同步采集该波长下的40幅连续干涉组图,最终得到4个波长下的160幅分辨率为964 像素×1 292像素的干涉组图。四波长干涉图像的数据处理流程如图2所示。
2.1 获取灰度均值序列
选取波长λk(k=1,2,3,4)干涉下的40幅连续干涉图像,先提取干涉图像像素点的灰度值,在此基础上,应用零点位置法取两组相位相差接近π/2的像素点,分别求和与平均,得到两组灰度均值序列。

图2 数据处理流程图Fig.2 Flow chart of data processing
2.2 计算初相位
对上述灰度均值序列曲线平滑处理后,进行椭圆拟合[13]。根据PZT相移,利用数学插值技术,从40幅干涉图中得到4幅相差π/2的干涉图。然后利用相移四步法可求得像素点的初相位。
2.3 计算远近波长相位差
取干涉场中心为参考零点,即设坐标(482,646)为参考零点,则此点的绝对高度和相位均值都为0,各波长的相位均以此为标准进行处理,即
φk(m,n)=φk(m,n)-φk(m0,n0)
(1)
式中:φk(m, n) 表示单个波k下的像素点的相位。数据处理时,取m0=482,n0=646,通过公式(2)扩展,使得φk(m, n)处于(-π,π)中间:
(2)
式中[ ]表示圆整运算。
在归零后的初相位基础上,分别按下式计算远近波长相位差:
(3)
图3为远近波长的相位差及某单个波长的初相位,其中近波长、远波长、较远波长的相位差在进行圆整处理后,处于(-π,π)之间。
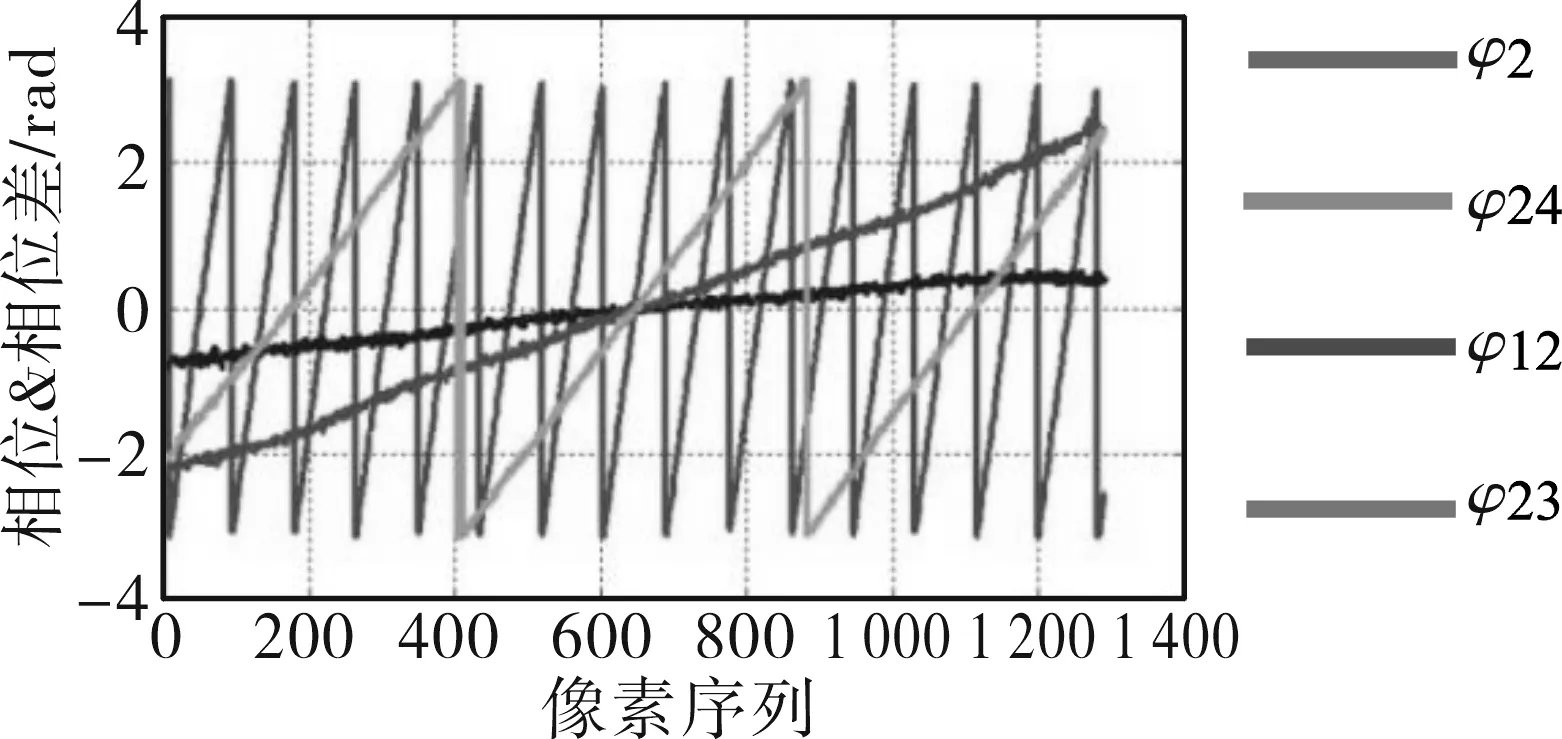
图3 相位及相位差Fig.3 Phase and phase difference
2.4 计算绝对高度
由干涉理论可推导出表面高度hmn满足如下公式:
(4)
式中:p1、p2为远波长和较远波长相位差的干涉级次;q为单波长相位下的干涉级次,近波长相位差的干涉级次为0。
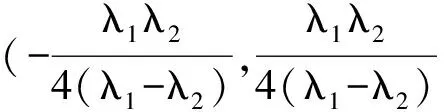
运用等效波长的思想,即λ12=λ1λ2/|λ1-λ2|,由公式(4)可以推导出不同波长下像素序列的绝对高度hmn:
(5)
在同等相位误差的条件下,等效波长的相位误差比单波长的大,而等效波长中近波长的相位误差又比远波长的大,所以,上式中,第一个的误差最大,最后一个的误差最小。在实际运用中,可以采用数据校正[14]的思想,对测量结果进行校正。在公式(5)中,即用第3个式子的测量结果校正第2个的数据,再用第2个的数据校正第一个的数据,最后用第一个的数据校正第4个的数据。
根据图3,首先计算某一像素点对应在近波长的相位差曲线上的相位φ12;其次通过φ12计算该点对应的较远波长、远波长相位差下的干涉级次p1、p2,并得到绝对相位φfar,φfar1,可得:
(6)
式中:[ ]表示圆整运算;k1、k2表示与波长相关的常数,圆整运算后即得出干涉级次p1、p2。
然后通过φfar1计算该点对应的单波长下的干涉级次q,得到单波长的绝对相位φsingle:
(7)
用φsingle计算该点相对于参考零点的绝对高度:
(8)
3 测量系统的精度分析与验证
采用一块方波多刻线表面粗糙度玻璃样板作被测表面,对该测量系统进行精度验证,该多刻线样板已于2014年9月由中国计量科学研究院根据国家粗糙度基准进行过校准,校准结果如下:轮廓算术平均偏差Ra=1.61μm,轮廓最大高度Rz=3.86μm,测量过程中,Ra与 Rz的扩展不确定度U95=5%。测量过程中使用上述测量系统与数据处理算法,运用近波长的相位差在大尺度范围内识别测量结果,远波长相位差在小尺度内进一步缩小测量结果的误差[15]的相位差大小尺度结合思想,最后用单波长相位计算最终测量结果,获得被测表面的高度信息,最终恢复出的方波多刻线玻璃样板的三维形貌如图4所示。

图4 方波多刻线三维形貌Fig.4 Area of 3-D topography of glass specimen
取方波样板的某一横截面进行分析,标定的像素尺寸为0.36 μm,评定长度为4 mm。在该评定长度内依次选取0.8 mm的取样长度对该横截面进行5次Ra的评定,评定结果Ra分别为1.673 7 μm,1.664 9 μm,1.675 8 μm,1.675 2 μm,1.667 4 μm,取最大值Ra=1.675 8 μm算得其表面粗糙度测量结果的相对误差为4.09%。
4 结论
采用Mirau相移干涉形式搭建的表面形貌的干涉测量系统,在保证相位识别精度的前提下,理论上实现了测量表面形貌的范围从原来的半波长扩展到13.26 μm,对640 nm波长而言,深度测量范围扩大到约41倍。测量过程中,4个波长轮流切换,运用相位差大小尺度结合的思想,从大尺度到小尺度逐步衔接与过渡,在每个尺度测量时保证其相应的识别精度。由于采用了误差校正的算法,因此,降低了对系统抗振和抗干扰的要求。
[1] Wang Haishan, Shi Tielin, Liao Guanglan,et al. Profilometer based on interferometry and micro vision system[J]. Opto-Electronic Engineering,2008,35(7):85-88. 王海珊,史铁林,廖光兰,等. 基于干涉显微原理的表面形貌测量系统[J] 光电工程,2008, 35(7):85-88.
[2] Wang Shuzhen, Xie Tiebang, Chang Suping. Vertical scanning white light interfering profilometer based on linnik interference microscope[J]. SPIE, 2010,7656:765631-1-6.
[3] Lehmann P. Vertical scanning white-light interference microscopy on curved microstructures [J]. Optics Letters, 2010, 35 (11):1768-1770.
[4] Yang Tianbo,Guo Hong, Li Dacheng. The summary of algorithms for the white light scanning interferometry [J]. Optical Technique,2006,32(1):115-118. 杨天博,郭宏,李达成.白光扫描干涉测量算法综述[J]. 光学技术, 2006,32(1):115-118.
[5] Li Juan. Research of 3-D surface topography measurement system with white light microscopic interference[D].Wuhan: Huazhong University of Science and Technology,2012. 李娟.白光显微干涉表面形貌三维测量系统的研究[D].武汉:华中科技大学,2012.
[6] Jiang Xiang, Wang Kaiwei, Gao Feng,et al. Fast surface measurement using wavelength scanning interferometry with compensation of environmental noise[J]. Applied Optics, 2010, 49 (15):2903-2909.
[7] Kuo C C,Kiyoshi T,Akihiro Y,et al. Calibration of wavelength scanning in wavelength scanning interferometer[J]. Journal of the Japan Society for Precision Engineering,2002, 68(3):392-396.
[8] Hata S, Hayashi J, Ishimaru I, et al. Nano-level 3-D measurement system using three wavelength laser light interference[C]. US:IEEE,2008.
[9] Zhou Mingbao. Interference in measuring the surface topography of method to expand the depth measuring range[J]. Optics and Precision Engineering, 1999,7(4):1-8. 周明宝. 干涉法表面形貌测量使用的拓展深度测量范围的方法[J].光学精密工程,1999,7(4):1-8.
[10]Dobosz M. Influence of laser diode wavelength tunability on the range, resolution and repeatability of interferometric distance measurement[J]. Optics & Laser Technology, 2008, 40:352-359.
[11]Zhang Hongxia, Zhang Yimo, Jing Wencai,et al. Mirau phase-shifting interferometer for microsurface topography measurement[J].Journal of Tianjin University, 2005,38(5):377-380. 张红霞,张以谟,井文才,等. 检测微表面形貌的Mirau相移干涉轮廓仪[J].天津大学学报,2005,38(5):377-380.
[12]Guan Xin,Wang Xuanze, Zhai Zhongsheng, et al. A driving step auto-access method for single wavelength microscopic interference [J].SPIE, 2014,9276:0U1-0U6.
[13]Wang Xuanze, Guo Jun, Xie Tiebang. Ellipse fit algorithm and subdivision revision method of precision diffraction grating[J]. Tool Engineering, 2003,37(12):47-49. 王选择, 郭军,谢铁邦. 精密衍射光栅信号的椭圆拟合与细分校正算法[J]. 工具技术 2003,37(12):47-49.
[14]Wang Wei. Multi-wavelength interferometry in the application of the nanometer scale measurement[D].WuHan: Hubei University of Technology, 2006. 汪威.多波长干涉法在纳米尺度测量中的应用[D].武汉:湖北工业大学,2006.
[15]Yang Liangen, Liu Bingkang, Wang Xuanze, et al. Method for improving precision of interferometric phase-recognization[J].Journal of Applied Optics,2015,36(4):590-595. 杨练根,刘丙康,王选择,等. 一种提高干涉相位识别精度的方法[J]. 应用光学,2015,36(4):590-595.
Four-wavelength switching interference measurement system for surface topography
Yang Liangen1, Yu Zaixin1, He Lang1, Wang Xuanze1,2
(1. School of Mechanical Engineering, Hubei University of Technology, Wuhan 430068, China; 2.State Key Laboratory of Precision Measuring Technology and Instruments, Tianjin University, Tianjin 300072,China)
Phase-shifting interferometry is an important measurement method for surface topography, but the depth measuring range is limited by the wavelength.A four-wavelength interference measurement system for surface topography was proposed.Through rotating the filters, 4 light sources with different wavelengths were switched out from LED light, and the single wavelength interference was conducted in turn. A data processing method for multiple wavelength interference images was put forward, which used the algorithm of elliptic fitting and the combination of varied scales to achieve wide-range high-precision surface topography measurement on the condition of calculating the phase point-by-point and frame-by-frame. Experimental results show that under the measurement depth expanded to nearly 41 times, the relative measurement error of surface roughness of square wave specimen with multiple grooves is only 4.09%,compared to the data calibrated by China Institute of Metrology. Therefore, the system can realize high-precision measurement for surface topography in a certain range.
phase-shifting interferometry;surface topography measurement;four-wavelength;phase difference; elliptic fitting
1002-2082(2015)06-0847-05
2015-03-25;
2015-07-13
国家自然科学基金资助项目(51275157,51275158,51175154)
杨练根(1965-),男,湖南平江人,博士,教授,主要从事精密测量与仪器和传感器技术等方面的研究。
E-mail:yanglg@mail.hbut.edu.cn
TN206;TH
A
10.5768/JAO201536.0601005

