大俯仰角度的两轴两框架平台稳定技术
李红光,纪 明,吴玉敬,郭新胜,彭 侠
(西安应用光学研究所, 陕西 西安 710065)
大俯仰角度的两轴两框架平台稳定技术
李红光,纪 明,吴玉敬,郭新胜,彭 侠
(西安应用光学研究所, 陕西 西安 710065)
为了解决大俯仰角度方位平台稳定性能降低的问题,利用两轴两框架稳定平台稳定原理,分析在传统方位陀螺安装方式下,大俯仰角度时方位平台稳定性能降低的原因以及正割补偿带来的噪声等问题,提出在方位平台上安装2个正交的方位、横滚陀螺,解算出瞄准线方位惯性角速度,从而实现大俯仰角度下的方位稳定控制方法。仿真实验验证了该方法可以提升大俯仰角度下两轴两框架平台的方位稳定控制性能,减小陀螺噪声对控制性能的影响,在同等条件下,方位稳定误差峰峰值由450 urad减小为250 urad。
光电稳定平台;两轴平台;大俯仰角度;瞄准线角速度
引言
目前,光电系统普遍采用的稳定平台是两轴结构,包括两轴两框架和两轴四框架,其中两轴两框架以其机构简单、成本低、体积小等特点,应用十分广泛。两轴两框架稳定平台通常采用两只陀螺作为惯性速率传感器,均安装在俯仰平台上,且2个敏感轴和光轴均正交,陀螺数据分别通过方位、俯仰控制电路驱动方位、俯仰电机,形成速率闭环,从而实现光电系统的稳定。从某些光电系统的战术指标来看,在稳定平台俯仰角度很大时仍需要正常瞄准跟踪目标,而此时两轴两框架稳定平台的方位轴的稳定性能降低,稳定指标已经无法满足系统要求[1-2]。本文在分析两轴两框架稳定平台稳定原理的基础上,针对该问题,提出了利用两只陀螺分别测量方位转台的方位轴与横滚轴的扰动速率,通过解算代替原来方位陀螺,实现方位平台的速率闭环控制,实现在俯仰角度很大时方位平台稳定性能基本保持不变。
本文通过简述两轴两框架稳定平台稳定原理,分析大俯仰角度时方位平台稳定性能降低的原因以及正割补偿带来的问题,通过理论分析,提出了在方位平台上安装方位陀螺、横滚陀螺实现瞄准线惯性速度测量,然后在方位控制回路加入正割补偿,从而实现光电系统瞄准线的稳定,最后通过仿真实验验证了该方法的能够提升大俯仰角度下两轴两框架平台的方位稳定控制性能,减小陀螺噪声对控制性能的影响。
1 两轴两框架稳定平台稳定原理简述
1.1 建立坐标系
在进行讨论之前,先建立两轴两框架稳定平台的坐标体系。
系统的结构与坐标的定义如图1所示。图中
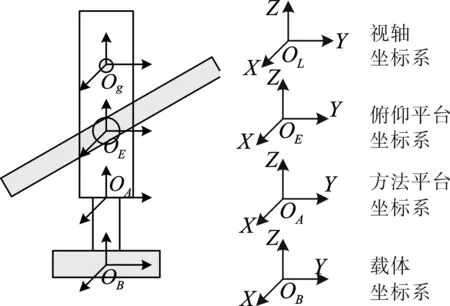
图1 反射镜稳定的坐标系示意图Fig.1 Schematic diagram of coordinates for mirror stabilization
1.2 稳定原理简述
系统的结构与坐标系定义如图1所示,通常陀螺直接安装于俯仰平台上,其2个敏感轴与光轴正交。各个坐标系相对运动关系如图2所示。
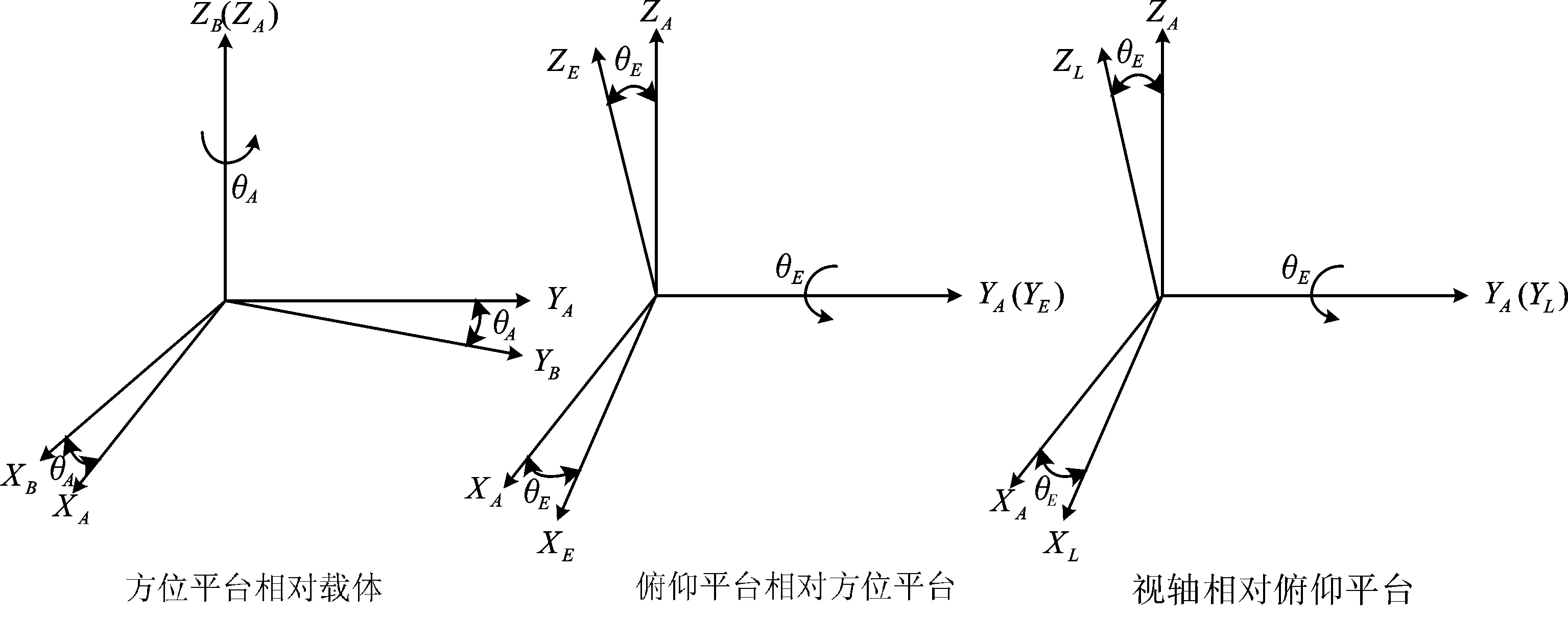
图2 坐标系相对关系示意图Fig.2 Schematic diagram of coordinates relation
设方位平台相对载体转动角度为θA,载体干扰角速度耦合到方位平台坐标系的方程为
(1)
设俯仰平台相对方位平台转动角度为θE,方位平台对俯仰平台的耦合关系为
(2)
由于光轴坐标系和俯仰平台坐标系时刻保持一致,因此方位平台对光轴坐标系的耦合关系为
(3)
将(3)式展开,将(1)式代入,可以得到视轴的方位和俯仰速度表达式:
(4)
陀螺敏感安装在俯仰平台上,用来测量瞄准线方位角速度和俯仰角速度,设陀螺敏感量分别为ωgY和ωgZ,则有:
(5)
由于光学传感器固定安装在俯仰平台上,方位、俯仰陀螺测量得到的结果就是光轴的惯性方位和俯仰角速度,用陀螺信号进行反馈,通过控制器控制方位、俯仰电机转动,使得光轴的方位角速度ωLY、俯仰角速度ωLZ等于零,实现光轴惯性空间方位、俯仰的稳定控制[3-5]。
2 大俯仰角时方位性能降低的原因
就方位闭环控制系统来看,方位陀螺随俯仰轴转动,敏感光轴方位轴的扰动信号,通过方位控制电路控制方位电机,形成速率闭环,实现方位轴稳定,此时的方位控制框图[6]如图3所示。当俯仰角度为零时,方位电机轴和方位陀螺敏感轴平行,方位陀螺的数据即是方位电机的转动速度;当俯仰转动θE时,由于方位陀螺随俯仰平台转动,此时方位陀螺测得的数据是方位电机转速的一个分量,即方位电机转速的cosθE倍,从控制理论来讲,方位速率闭环控制回路的总增益系数降低,方位控制性能下降。
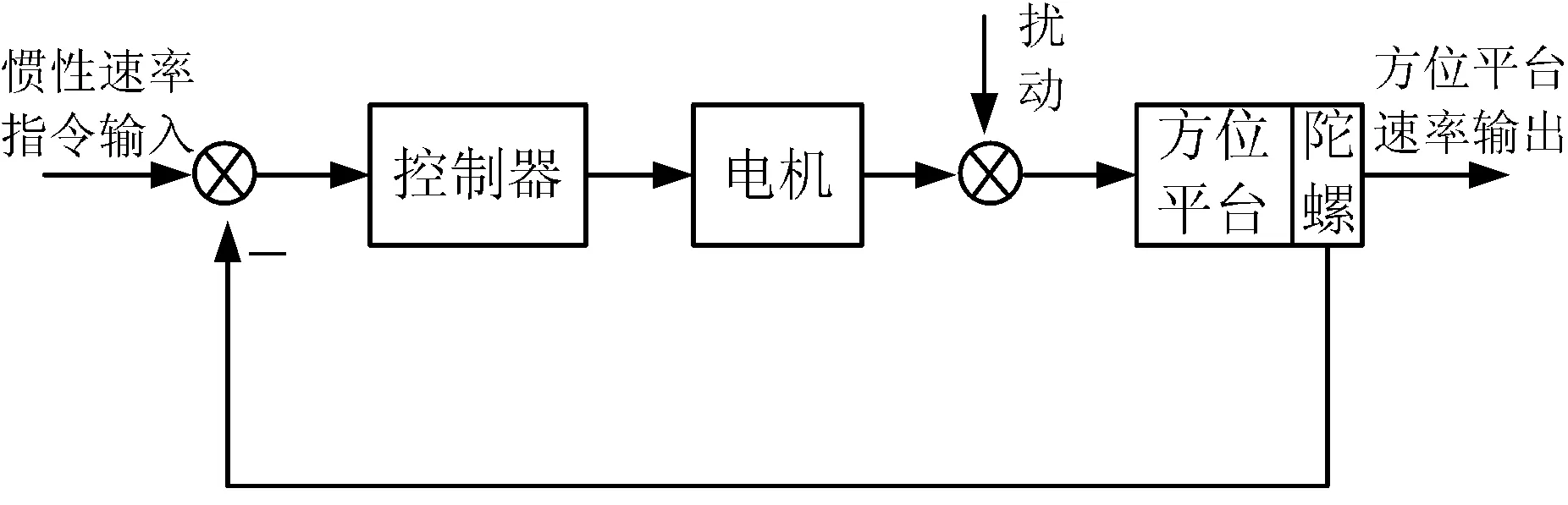
图3 方位控制框图Fig.3 Block diagram of azimuth control
在两种情况下,方位控制回路开环波特图如图4所示,图中无标识曲线为俯仰角度为0°时方位控制系统开环波特图,在10Hz处幅频特性值9.76dB;图中标×曲线为俯仰角度为30°时,方位控制系统开环波特图,在10Hz处幅频特性8.5dB,前者总增益是后者总增益的1.154 78倍,如果俯仰角度增大,两者相差更大,但两者的相频特性相同。
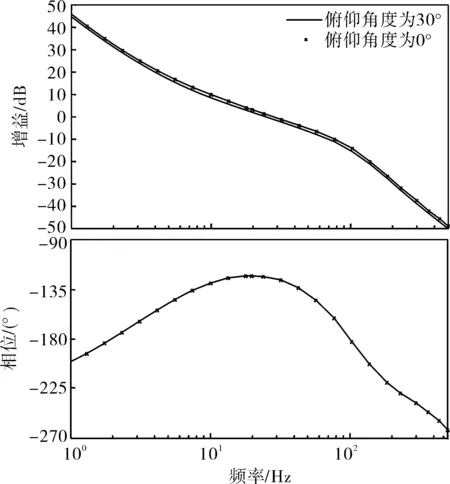
图4 俯仰在不同位置时方位回路开环波特图Fig.4 Bode plot of azimuth open loop at different pitching positions
因此,俯仰角度较大时,两轴两框架稳定平台需要对方位速率闭环回路进行正割补偿,此时的方位控制框图如图5所示,在任意俯仰角度下,方位控制回路的开环特性曲线如图6所示,与没有正割补偿时俯仰处于零位的方位控制回路的开环特性曲线相同。通常,为了获得很好的控制性能,在俯仰角度为零时,假设方位回路的增益选择最佳值,如果对方位回路直接进行正割补偿,不同俯仰角度下整个闭环系统对陀螺数据的放大系数不同,由于陀螺噪声的存在[7],造成方位控制性能并没有明显好转,尤其是在俯仰角度较大时,极易出现方位控制闭环不稳定现象。
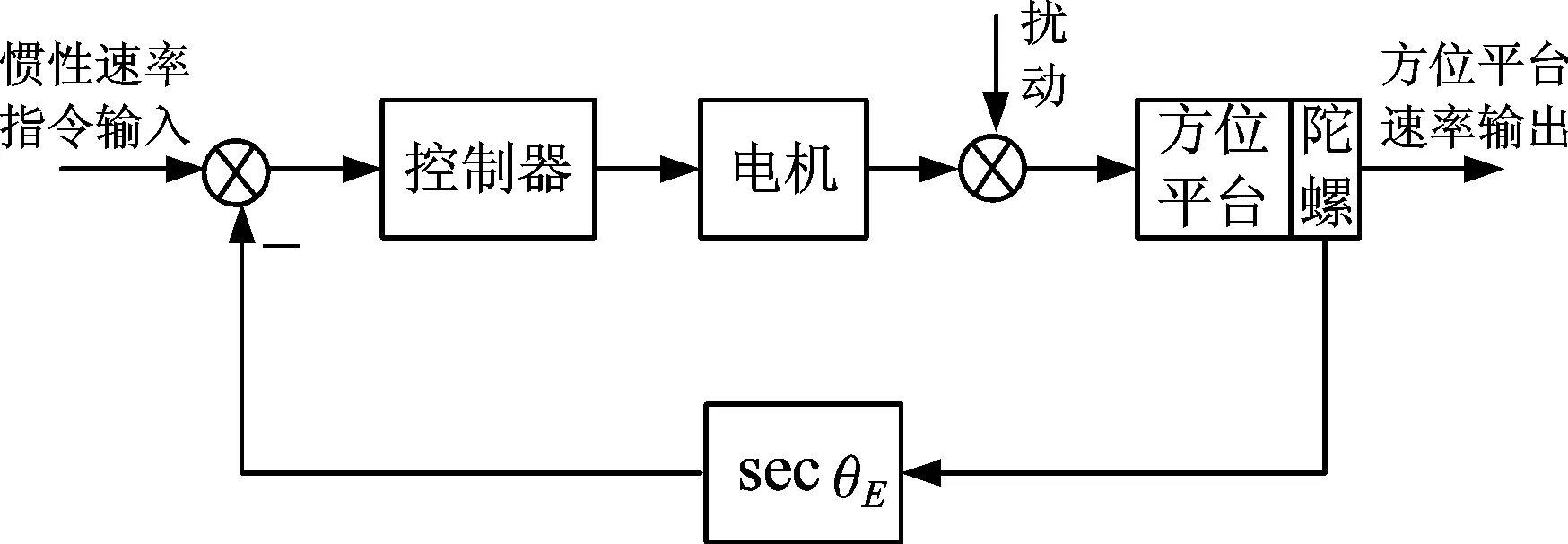
图5 正割补偿方位控制框图Fig.5 Block diagram of azimuth control with secant compensation
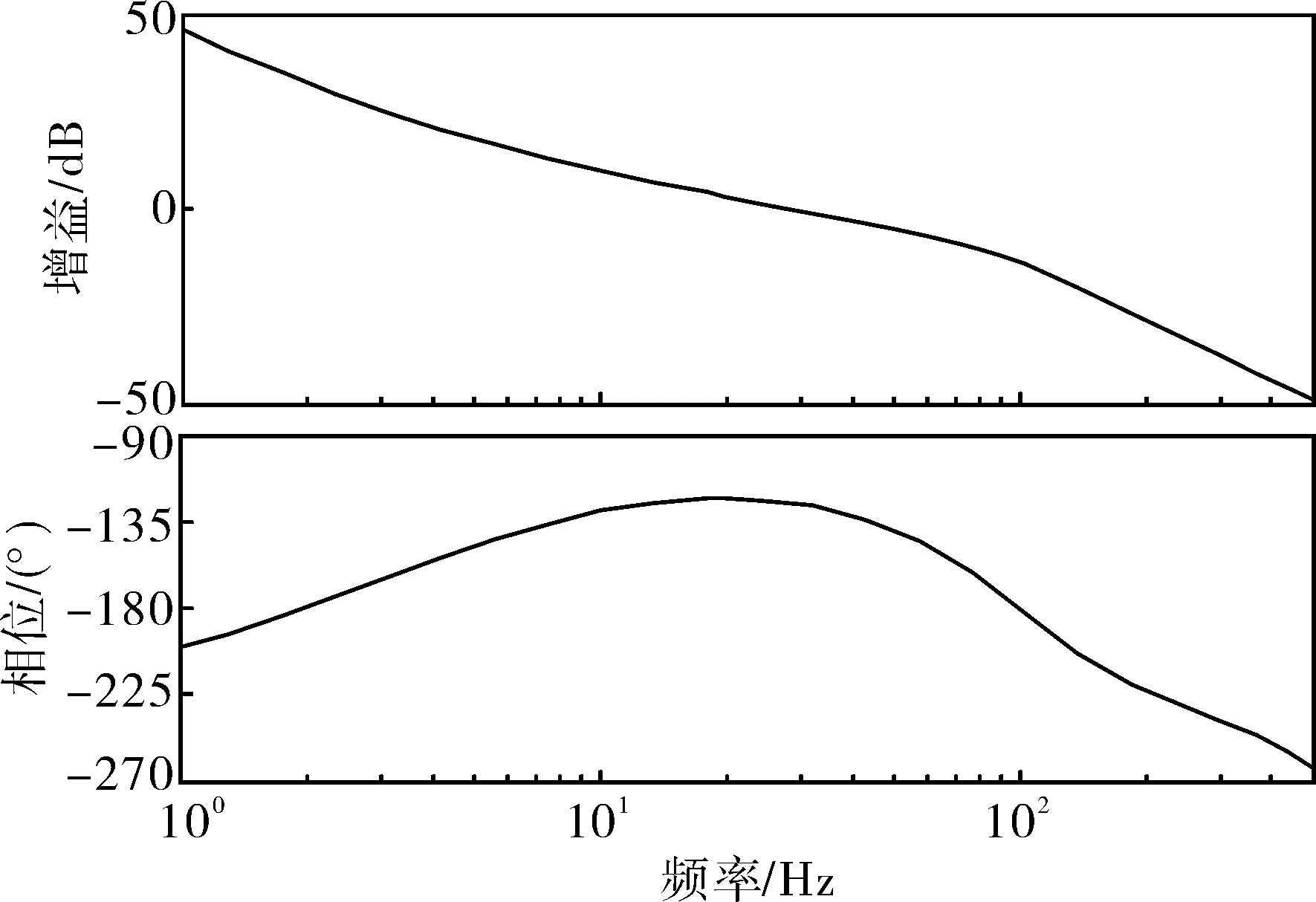
图6 正割补偿的方位控制回路开环特性曲线 Fig.6 Open loop characteristic curve of azimuth control with secant compensation
因此,需要寻找一种光轴惯性速率的测量方法及方位闭环控制方法,既能测量出光轴的方位速率数据,又保证在控制回路中加入正割补偿后不会造成陀螺噪声被放大。
3 大俯仰角稳定平台方位控制回路设计方法
3.1 瞄准线惯性速率测量方法
根据上述两轴两框架稳定原理的分析,依据公式(1)、公式(2)和公式(3),可以得到瞄准线的惯性空间下的速度表达式为
ωLZ=ωAX·sinθE+ωAZ·cosθE
(6)
因此,考虑在方位平台上安装两只陀螺,在俯仰平台上安装一只陀螺,代替传统稳定平台中俯仰平台的两只陀螺。方位平台上的两只陀螺正交,测量方位平台的ωAX和ωAZ,即方位平台的方位速率和横滚速率,然后由(6)式求解出瞄准线方位速率ωLZ,代替原来的方位陀螺ωgZ。俯仰平台上的陀螺测量瞄准线俯仰速率ωLY的方法与传统的测量方法相同,俯仰控制回路也不变。因此,本文只研究方位控制回路设计方法。
3.2 方位控制回路设计方法
方位控制回路框图如图7所示,控制回路由控制器、电机、方位平台及负载、方位陀螺、横滚陀螺、瞄准线速度解算模块、正割补偿构成。
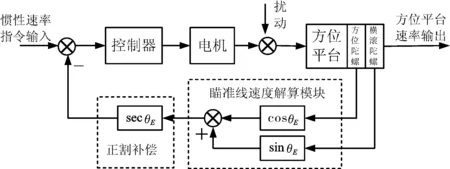
图7 方位控制回路框图Fig.7 Block diagram of azimuth control loop
依据公式(6)求出瞄准线方位速率,在控制回路中对其进行正割补偿,即
secθE·ωLZ=secθE·(ωAX·sinθE+
ωAZ·cosθE)=tgθE·ωAX+ωAZ
(7)
式中ωAX和ωAZ分别为方位平台上两只陀螺的输出。从公式(7)可以看出,在正割补偿后,方位平台上的方位陀螺ωAZ的噪声的放大倍率并没有变化,而方位平台上的横滚陀螺ωAX的噪声放大了tanθE倍,而在俯仰角度θE小于45°时,tanθE<1,相当于横滚陀螺ωAX的噪声并没有放大反而减小。利用两种测速方法得到瞄准线方位角速率经过整个补偿后的波形如图8和图9所示,此时俯仰角度为30°,测试时瞄准线方位轴与速率转台的旋转轴平行,速率转台转动速率为5°/s,传统方法测量的瞄准线角速度均值为5.044 4°/s,利用两只正交陀螺测量的瞄准线角速度为5.043 2°/s,比较图8和图9比较可以看出,正割补偿后传统方法测量的瞄准线速率信号白噪声较大。
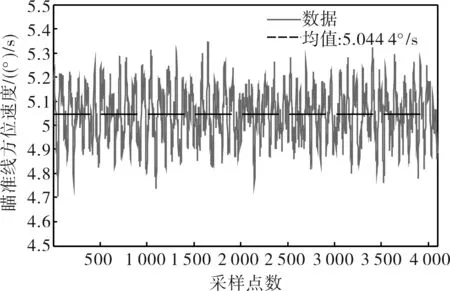
图8 传统测速量的瞄准线方位速度Fig.8 Azimuth velocity of LOS measured by tradition method
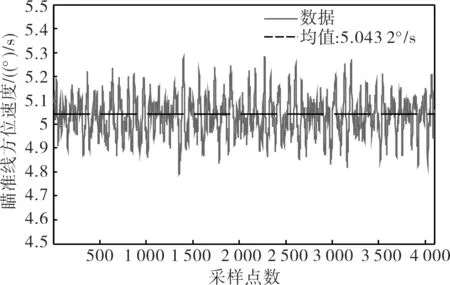
图9 两只陀螺测量的瞄准线方位速度Fig.9 Azimuth velocity of LOS measured by two gyros
因此,上述瞄准线惯性速率测量方式,在对方位控制系统进行正割补偿时,避免了方位控制系统中陀螺噪声对控制性能的影响;此时俯仰控制系统没有变化,保证了整个系统的稳定性能。
4 方位控制回路仿真
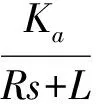
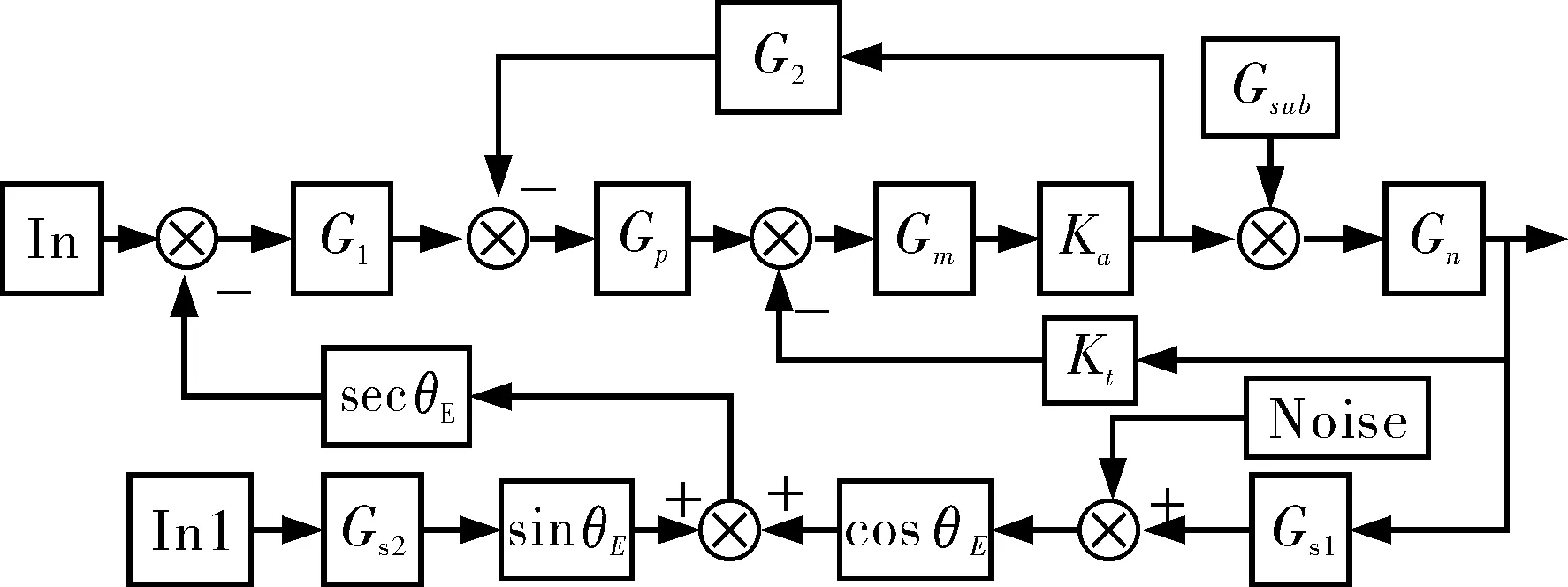
图10 方位控制回路仿真模型图Fig.10 Simulation diagram of azimuth control loop
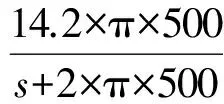
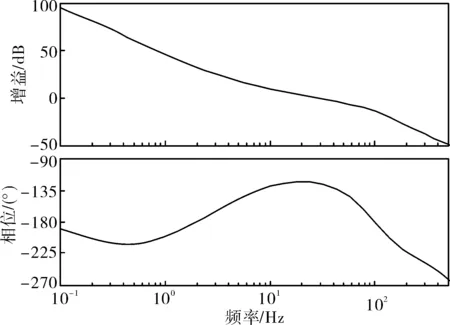
图11 方位控制回路开环波特图Fig.11 Bode plot of azimuth control open loop
图10中输入点In为系统指令输入点,输入点In1为方位平台的横滚扰动,仿真时采用1hz正弦选信号。子系统Gsub为摩擦力矩生成模型,载体扰动在方位平台方位向的分量通过此模型转换为扰动力矩进入模型,其输入为平台运动速度和最大静态摩擦力矩[9-10],其输出波形如图12所示。Noise为陀螺信号的噪声,如图13所示。
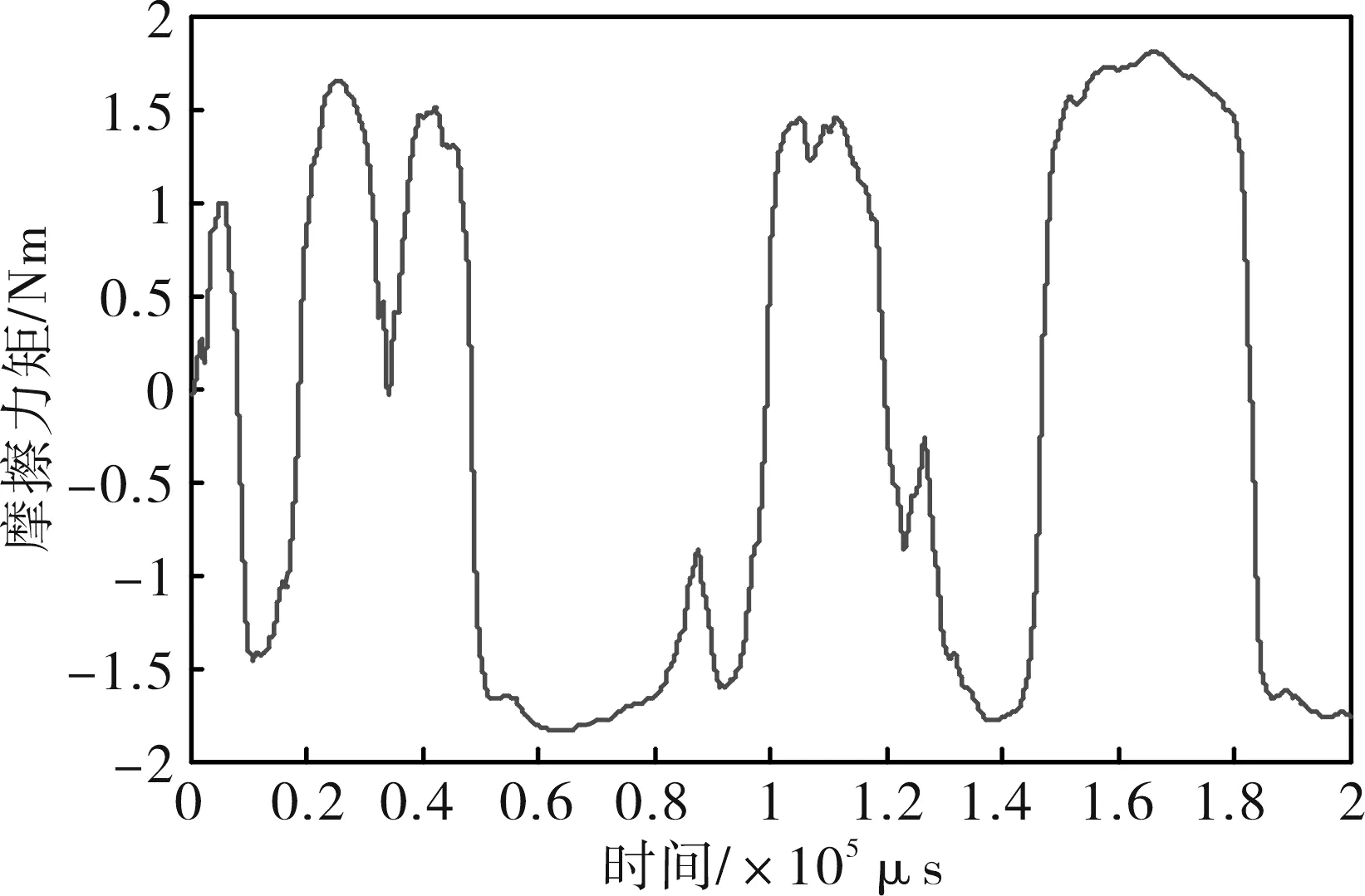
图12 摩擦力矩波形Fig.12 Waveform of friction moment
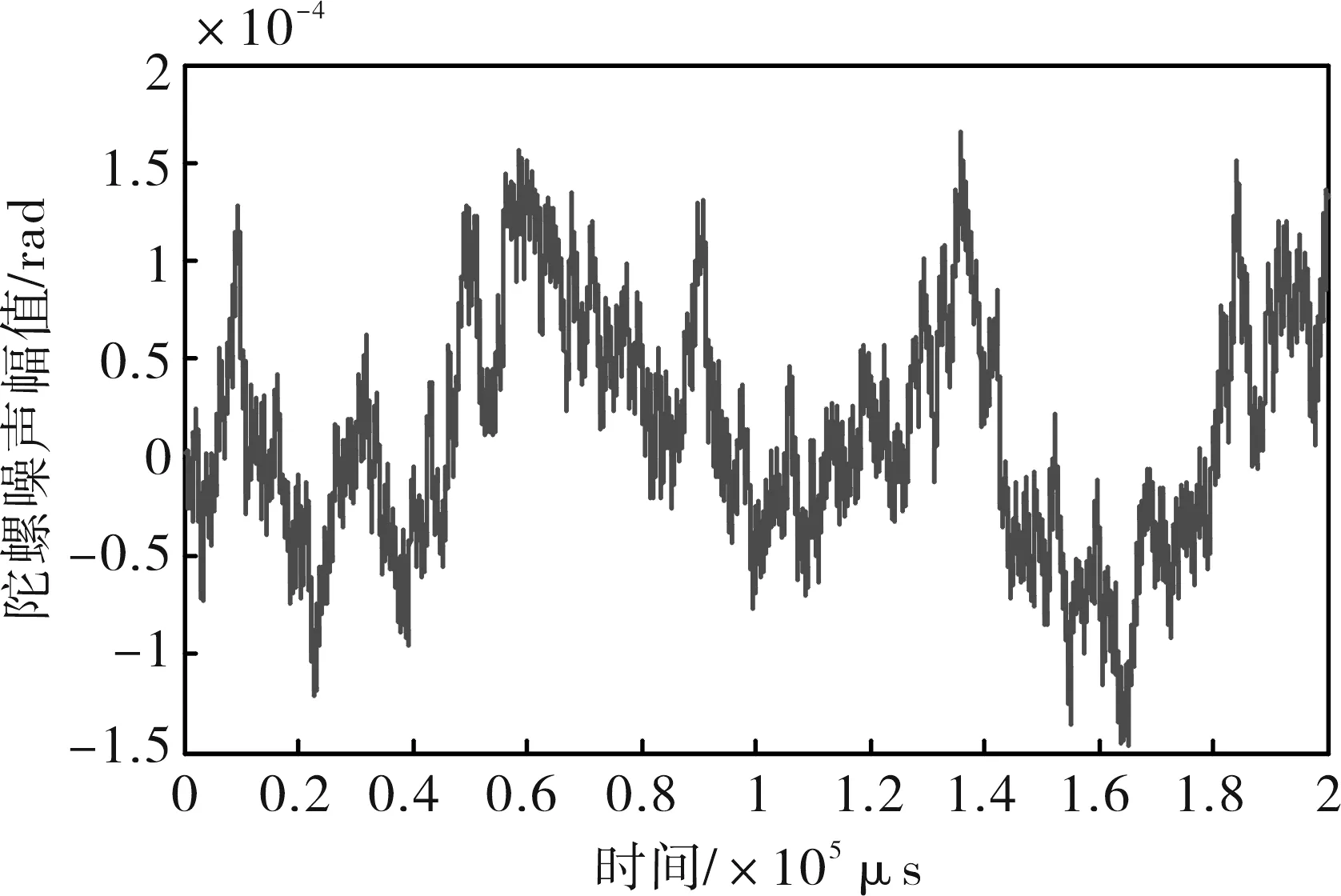
图13 陀螺噪声波形Fig.13 Waveform of gyro noise
仿真时俯仰角度为1rad,其稳定误差曲线如图14所示,图中LOS2曲线为利用传统安装方式
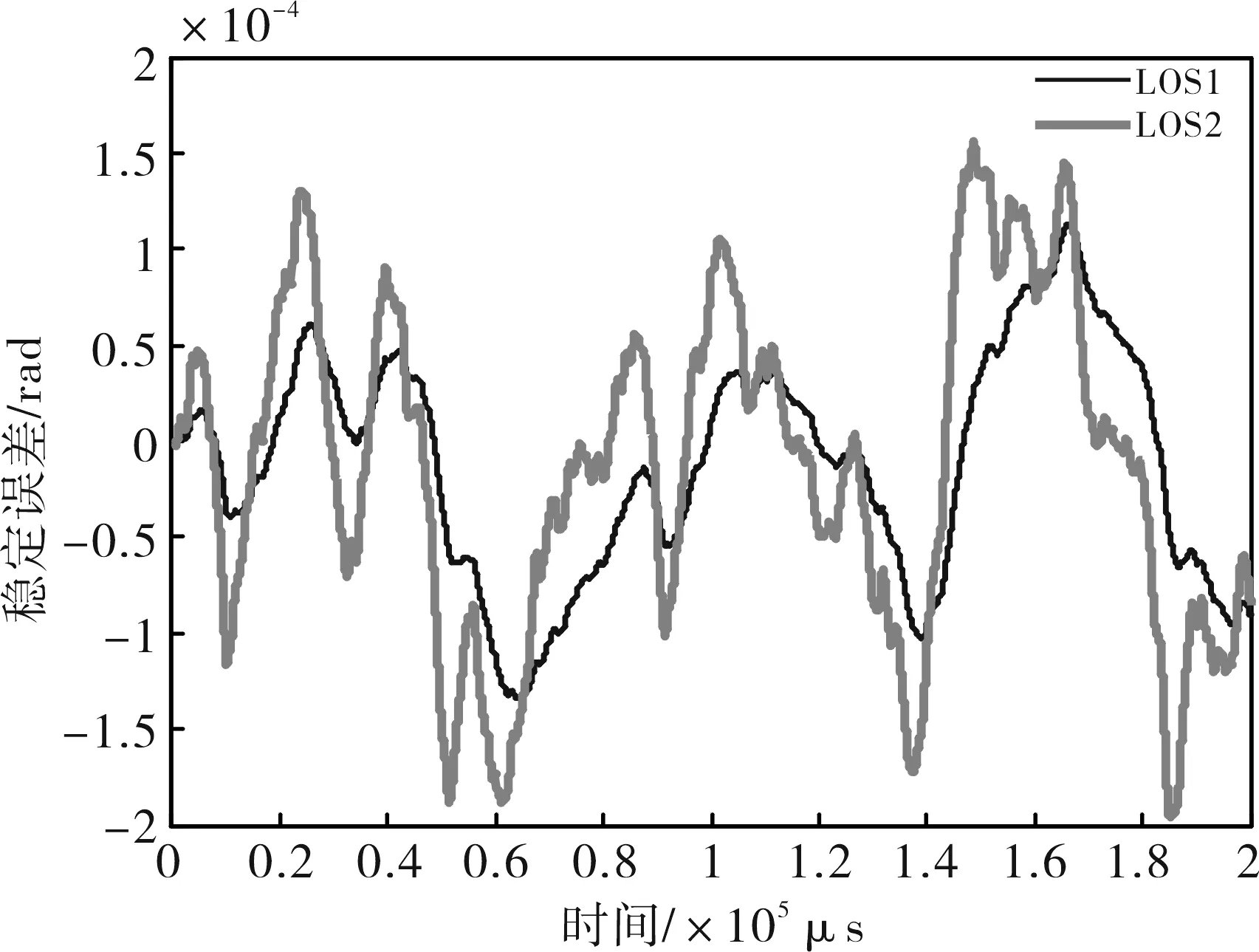
图14 稳定误差比较Fig.14 Comparison of stabilized error
的方位陀螺作为瞄准线惯性速度传感器时,方位轴的稳定误差曲线,其峰峰值为450μrad。LOS1曲线为同等条件下,在方位平台上安装方位和横滚陀螺作为瞄准线的惯性速度传感器时,方位向的稳定误差曲线,LOS1误差曲线明显小于LOS2误差曲线,其稳定误差峰峰值在250μrad以内。
5 结束语
本文从两轴两框架稳定平台稳定原理出发,分析在传统方位陀螺安装方式下,大俯仰角度时方位平台稳定性能降低的原因以及方位控制回路对方位陀螺信号正割补偿带来的问题,提出通过在方位平台上安装两只正交的方位、横滚陀螺,解算出瞄准线方位惯性角速度的方法,通过正割补偿,实现大俯仰角度下的稳定控制。理论分析及仿真结果表明,本文提出的方法满足在惯性空间下两轴两框架光电系统瞄准线速度测量需求,在大俯仰角度下,方位控制回路的性能几乎没有变化,而且避免了正割补偿带来的控制回路噪声问题,较传统陀螺安装方式下的方位稳定性能有所提升,从而实现了大俯仰角度下光电系统瞄准线的稳定。该方法瞄准线的惯性速度是依据俯仰角度对方位陀螺、横滚陀螺解算得到,因此,系统对俯仰角度测量精度提出了一定的要求。
[1]WangHui,BianShuancheng.Studyonstabilizationtechnologyforgyroscpe-stabilizedplatformunderlargepintchingangle[J].MicrocomputerInformation, 2012,28(6):32-33. 王辉,边栓成.两轴稳定平台大俯仰角状态控制技术研究[J].微计算机信息, 2012,28(6):32-33.
[2]DongXiaomeng,ZhangPing.Zenithblindzoneoftwo-axisstabilizedplatform[J].JournalofBeijingUniversityofAeronauticsandAstronautics, 2007,33(7):811-815. 董小萌,张平.两轴稳定平台的过顶盲区问题[J].北京航空航天大学学报, 2007,33(7):811-815.
[3]FanDapeng,ZhangZhiyong,FanShixun,etal.ResearchofbasicprinciplesofE-Ostabilizationandtrackingdevices[J].OpticsandPrecisionEngineering, 2006,14(4):673-679. 范大鹏,张智永,范世珣,等.光电稳定跟踪装置的稳定机理分析研究[J].光学精密工程, 2006,14(4):673-679.
[4]HilkertJM.InertiallyStabilizedplatformtechnology[J].IEEE, 2008,28(1):26-46.
[5]JiMing.Isolationandcompensationofmovementforstabiliztionoptics-electricalsystemwithhighaccuracy[J].ActaArmamentarii, 1996, 17(4):320-324. 纪明. 高精度光电二级稳定系统的运动隔离与补偿分析[J].兵工学报,1996,17(4):320-324.
[6]ZhangZhiyong,FanDapeng,FanShixun.ServosystemdesignforE-Ostabilizationandtrackingdevices[J].OpticsandPrecisionEngineering, 2006,14(4):681-690. 张智永,范大鹏,范世询.光电稳定跟踪装置的控制系统设计[J].光学精密工程,2006,14(4):681-690.
[7]JiMing.Simulationanderroranalysisofmirrorstabilizedsystem[J].JournalofAppliedOptics, 2000,21(5):19-22. 纪明.反射镜稳定系统的仿真与误差分析[J].应用光学,2000,21(5):19-22.
[8]WuYujing,JiMing.Compensationtechnologyforhighvelocitytrackingofelectro-opticalpod[J].JournalofAppliedOptics,2006,27 (4):293-297. 吴玉敬,纪明.光电吊舱大速率平稳跟踪补偿技术研究[J].应用光学,2006,27 (4):293-297.
[9]WangShijing,YangMing,DongHao.Variablestructurecontrolbasedonstabilizedplatformconsideringfrictioncharacteristic[J].ComputerSimulation, 2009,26(5):332-336. 王石静,杨明,董浩.考虑摩擦特性的稳定平台变结构控制研究[J]. 计算机仿真,2009,26(5):332-336.
[10]XunQingqing,WuYujing,ZhangJingyue,etal.ResearchonmodelingofstabilizedaimcontrolsystembasedondSPACE[J].ActaArmamentarii,2011,11:1423-1427. 胥青青,吴玉敬,张璟玥,姜世洲.基于dSPACE平台的稳瞄控制系统建模方法研究[J].兵工学报,2011,11:1423-1427.
Stabilization technology for two-axis two-framework platformwith big pitching angle
Li Hongguang,Ji Ming,Wu Yujing,Guo Xinsheng,Peng Xia
(Xi’an Institue of Applied Optics, Xi’an 710065, China)
In order to resolve the issue of azimuth platform stability depressing, by using the stabilization principle of two-axis two-framework platform, the reason for the stability depressing and the noise caused by secant compensation of azimuth platform were analyzed,which worked in big pitching angle with azimuth gyro of tradition fixing mode. We proposed to install an azimuth gyro and a roll gyro,which were orthogonal, on the azimuth platform to calculate the inertial azimuth angle velocity of line of sight,and realized the controlling method of azimuth stability with big pitching angle. Simulation experiment validates that, the azimuth stability controlling performance of the two-axis two-framework platform with big pitching angle can be advanced and the influence of gyro noise on the controlling performance can be depressed by using the method. Under the same conditions, the peak-to-peak error of azimuth stabilization can reduce form 450 urad to 250 urad.
EO stabilization platform ; two axes platform; big pitching angle; angle velocity of line of sight
1002-2082(2015)06-0823-06
2015-07-20;
2015-09-23
李红光(1983-),男,山东巨野人,博士研究生,主要从事光电系统及稳定跟踪技术研究。
E-mail:redlight007@163.com
TN29
A
10.5768/JAO201536.0601001

