启发式牙颌CT影像自动分割

黄志伟 戴 宁 刘 浩

(南京航空航天大学机电学院，南京 210016)

引言

计算机图形图像处理技术的发展和CT影像技术的广泛应用，为病灶的诊断和治疗提供了新的手段［1－2］。CT影像技术的应用主要包含切片数据三维重构、特征提取、外科手术模拟和放射性治疗精确定位等［3］。

图像分割是CT影像技术应用的关键步骤，CT图像序列分割可以分为像素分割和轮廓分割。像素分割是指通过区域增长或阈值设定的方法来增强具有相同特性的像素，但缺点是存在边界泄露。轮廓分割分为两类:一类是对象表面的演化［4］，另一类是对象轮廓的层层提取［5－6］。基于表面演化的方法提高了提取轮廓的精度，但比较耗时。轮廓层层提取的方法是近几年研究的热点，但有两个主要的难点:一是单幅图像轮廓如何准确获取，代表性方法有蛇形逼近法［7－8］;另一个是如何快速获取切片序列轮廓，CT图像通常包含几十张甚至上百张切片，如果通过人工对每一张切片进行交互分割，不仅效率低而且容易出错。

CT轮廓的自动提取可以最大程度地减少用户交互操作时间，许多学者对自动提取方法进行了研究［9－12］。侯等提出了基于快速行进法(FMM)，实现肝脏CT图像序列自动分割［9］。首先通过滤波处理，得到速率系数图像;然后根据CT图像相邻层的相似性，计算FMM所需的参数;最后根据这些参数进行图像分割。Pu等采用分段边界行进算法(ABM)，对 肺 CT 图 片 进 行 自 动 分 割［10］。Ciecholewski提出了基于逼近模型的方法，自动提取肝脏轮廓，通过构建多线段逼近肝脏近似轮廓，并取得了很好的效果［12］。

由于牙齿轮廓曲率较大且相邻牙齿间距较小，因此上述用于肝脏和肺部轮廓的提取方法难以适用于牙齿轮廓提取。张等提出一种牙的半自动分割方法，先利用包围盒技术获得待处理切片，然后用种子生长算法获取牙轮廓［13］。但是，此方法所需参数需要手动输入，操作比较繁琐。

口腔牙颌模型的快速重建对牙齿正畸、修复等具有重要意义。通过分析上述轮廓自动提取算法的优缺点，笔者提出一种基于启发式的CT轮廓自动提取方法。首先手动提取第一层切片轮廓，并将其匹配映射到下一层切片上;根据原始轮廓和待提取轮廓之间的对应点向量关系，使用收缩包围算法;同理，将得到的下一层轮廓映射到相邻层切片上，然后根据轮廓对应点的坐标值和法向量拟合轮廓边缘像素点。采用启发式的CT轮廓自动提取算法，大大缩短了轮廓提取的时间。

1 技术路线

牙齿间距较小，相邻牙齿之间存在粘连区，针对这一特点，设计具体的技术路线如图1所示。

1)通过拉普拉斯算子，对边界进行增强。

2)交互拾取特征区轮廓作为启发式轮廓自动分割的首张轮廓线。

3)将首张轮廓线映射到下层切片，作为收缩包围算法的初始轮廓。

4)用收缩包围算法，逼近待提取特征区的像素轮廓。轮廓收缩时先计算原始曲线上的极大曲率点，用这些曲率点构造控制多边形，然后分情况判断轮廓收缩方向。对于可直接判断上下层轮廓大小的情况，则直接向内或者向外用收缩包围算法;对于轮廓有交叉的情况，就每一个控制点的最大曲率处作法向射线，射线与轮廓线的内部和外部像素点相交，通过设置一个门限值决定轮廓收缩方向。在收缩过程中，采用可局部变形的四点Binary插值细分算法［14］，通过定义N个顶点构成闭合折线，然后四点插值来细分曲线。

图1 CT影像牙齿序列自动分割流程Fig.1 Femoral CT image automatic segmentation technology flowchart

5)以位移权重系数作为轮廓线逼近是否终止的判断标准。

2 CT轮廓自动提取

2.1 拉普拉斯算子轮廓增强

牙齿边界轮廓质量的好坏直接关系到轮廓分割的准确性。笔者提出一种CT图像轮廓增强算法:首先用图像边缘检测的方法检测CT切片的亮度梯度，得到边界轮廓(见图2(b))，然后将得到的轮廓和原始CT切片配准叠加得到边缘轮廓增强的CT图片(见图2(c))。通过实验比较Sobel、prewitt、roberts、拉普拉斯和 Canny等多种边缘检测算子［15－17］，发现 Canny边缘检测算子最优。但是，Canny算子得到的是边缘抑制后的单宽度像素轮廓，难以计算边缘像素点内外法向向量，并且将冗余轮廓线全部提取出来将导致后来收缩方向的判断难度增加。拉普拉斯算子较其他几种边缘检测算子不仅可以获得双像素边界，而且边界提取精度相对其他几种算子更高，所以综合考虑笔者选择拉普拉斯边缘检测算子。

图2 Laplace算子原始切片轮廓增强。(a)原始切片;(b)边缘检测;(c)轮廓增强Fig.2 Original slice contour is enhanced by Laplace operator.(a)Original slice;(b)Edge detection;(c)Contour enhancement

2.2 启发式分割过程

牙齿上下层轮廓的形状和位置非常相似，利用相似继承的原理，提出基于启发式的牙齿轮廓自动分割法，具体过程如下:首先，将手动提取的第一层切片轮廓装入初始轮廓链表，然后将此初始轮廓匹配映射到下一层切片上，根据原始轮廓和待提取轮廓之间的对应点向量关系使用收缩包围算法。同样，将得到的下一层轮廓装入初始轮廓链表，并且映射到下一层切片上;然后，根据轮廓对应点的坐标值和法向量拟合轮廓边缘像素点。牙齿轮廓的大小从上往下是个不断变化的过程，两层轮廓的逼近方向共分为3种类型。

1)上一层轮廓完全包围下一层轮廓，即Sn－Sn+1＞0，此时用向内收缩包围算法逼近下一层轮廓。

2)上一层轮廓完全位于下一层轮廓内部，即Sn－Sn+1＜0，此时用向外收缩包围算法逼近下一层轮廓。

3)上一层和下一层轮廓存在交叉无法直接判断，笔者通过门限值设定来决定轮廓收缩方向。

在图3中，Sn和Sn+1分别表示第n和第n+1层轮廓所围成的面积。在Sn－Sn+1＞0时，向内收缩包围如图(4)所示;同理，可以得到Sn－Sn+1＜0的轮廓向外收缩包围的过程;对于Sn和Sn+1存在交叉无法直接判断大小的情况，将在下一节叙述。

在图4中，切片Tn上的轮廓Bn映射到下一层切片Tn+1上，通过轮廓收缩包围算法，逐渐逼近待提取轮廓Bn+1，生成拟合轮廓Bn，n+1。同理，把得到的Bn，n+1当作上一层轮廓，映射到下一层切片上作为初始轮廓。然后，逼近Bn+2生成Bn+1，n+2，往复循环，最终实现启发式轮廓提取。

图3 轮廓收缩方向判断流程Fig.3 Illustrating the contracting direction in terms of flowchart

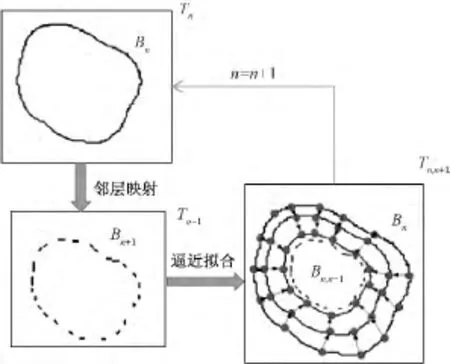
图4 第n层轮廓收缩逼近n+1层像素轮廓Fig.4 The n th layer contour approaches the(n+1)th pixel contour

切片Tn匹配映射到切片Tn+1后，用符号Tn，n+1表示为

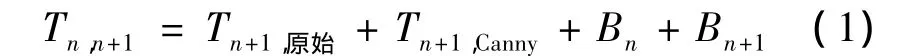
采用收缩包围算法，将初始轮廓Bn逐步拟合到待提取像素轮廓Bn+1，生成最终拟合轮廓Bn，n+1，有

最后，Tn+1层切片只含有拟合后的轮廓，即

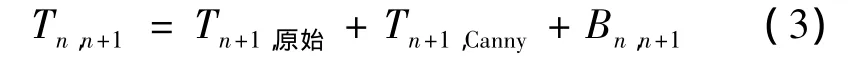
上述过程的伪代码为

2.3 收缩包围算法轮廓逼近

为了使上一层的闭合轮廓线都尽可能地逼近待提取轮廓，将文献［18］中的收缩包围算法推广到CT数据离散像素点拟合，通过调整初始轮廓上控制点来逐渐逼近待提取像素轮廓。收缩包围算法、蛇形算法以及变形算法比较相似，都是通过最优化边界轮廓来获得二维或三维的原始轮廓。最优化是通过内部稳定力(弯曲能量最小化)和将像素点拉向轮廓的外力，外部力通常来自于二维或三维标量场的梯度。本研究采用收缩包围算法，作用力分别是基于法向的吸引力和切向的松弛力，下面先介绍法向吸引力作用过程。

1)如果上层轮廓包围下一层轮廓，则向内用收缩包围算法，反之则向外用收缩包围算法;如果轮廓交叉不能直接判断向外还是向内收缩，就通过设定门限值判断轮廓收缩方向来获得符合要求的离散像素点。先找到已知轮廓线曲率极大值点，由这些点构建控制多边形(见图5(a))。沿一个曲率极大值点构建法方向向量np(见图5(b))，并取得与轮廓外像素的交点，建立离散点和已知曲率极大值点的一一映射(见图6(a))。常用的方法是最近投影点法［19］，即求离散点pi到已知轮廓X(S)上点qi的最短距离，有

式中，S*为pi在初始轮廓上最近点的参数。

在图5(b)中，水红色的点qi是初始轮廓线上曲率极大值点，np是其中一个极大值点的法向量;pi是待逼近的轮廓像素点，nc是np法向向量与pi交点像素的法向量;si是外部像素点，ns是np法向向量与si交点处像素的法向量。因为曲率极大值点的法向量np与初始轮廓线以外的像素点不止一个交点，所以无法直接判断曲率极大值点的收缩逼近方向。笔者通过门限值设定法解决此问题。

已知曲率极大值处的法向量np以及与np相交的交点像素法向量nc和ns。规定np·n≥δ，通过设定门限值δ来决定初始轮廓的逼近方向。设定δ＞0，由图5(b)可以看出，ns和np方向相反，nc和np方向相同。所以，此处初始轮廓向内收缩。初始轮廓线上另一点曲率极大值点的法向量为np1，与轮廓外像素和轮廓内像素交点的法向量分别是nc1、ns1。由图5(b)可以看到，np1的方向与nc1方向相同，与ns1方向相反，所以np1·nc1＞δ，此处控制顶点向外采用收缩包围算法。

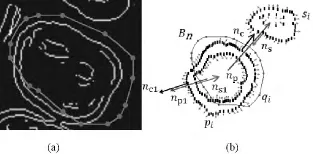
图5 交叉轮廓收缩方向判定。(a)构建控制多边形;(b)门限法原理Fig.5 Determine the contracting direction in intersected situation.(a)Constructthe control polygon;(b)Principle of the threshold

图6 轮廓包围算法逼近原始轮廓。(a)投影点一一映射;(b)轮廓拟合Fig.6 Approaching the initial outline with the shrinkwrapping algorithm.(a)One-to-one mapping;(b)Contour fitting

为了在位移过程中使qi点最大限度地逼近pi点，引入了位移权重系数［20］，通过设计权重矩阵来量化和评估点对的接近程度。权重矩阵M为对角矩阵，维数为n×n，n的大小为初始轮廓曲率极大值点的个数，于是权重矩阵为

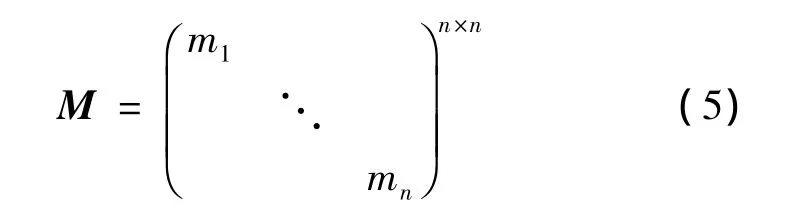
权重系数越大，表示当前点在移动过程中的影响力越大，即此点与目标点的位置越接近。设mi表示第i点的权重系数，则

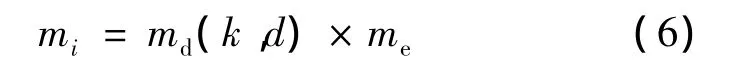
式中，md(k，d)为位移权重函数，k为当前迭代次数，d为当前移动点q'i与目标点pi之间的距离。

me代表两移动点之间曲线能量函数，有

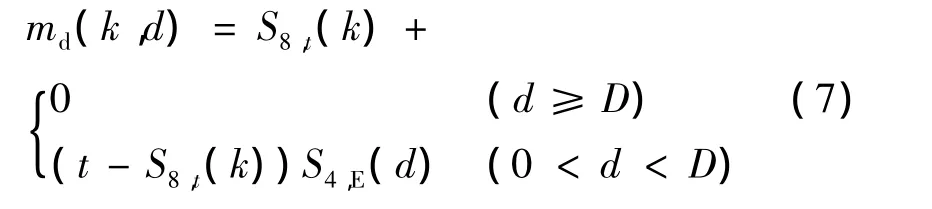
式中，D为有效距离，S8，t(k)为支撑函数。

式中，X(S)表示沿着参数s方向的轮廓;在点移动过程中，随着与目标点之间的距离逐渐缩小，md(k，d)逐渐增大，me增大，所以mi逐渐增大。

2)对于原始轮廓上的每一点qi，先用吸引力作用，再用松弛力作用。松弛力作用相当于对曲线进行光滑，使曲线上的点尽可能地均匀分布。由于收缩包围算法拟合内部像素点，只得到边界轮廓的大致形状，并不光滑，所以本研究采用可局部变形的四点binary插值细分算法，通过这些边界点生成连续光滑的曲线。

2.4 算法验证

所提出算法的实验平台为主频2.93 GHz、Core2处理器、4.00 GB内存的DELL PC，CT数据分别在10.01版本的Mimics软件［21］(比利时Materlise公司)和5.4版本的Amira(美国VSG公司)软件上进行数据重建。开发环境为VS2008，模型渲染基于OpenGL2.0图形库。

图7 不同初始权值曲线光滑程度对比。(a)控制多边形;(b)=0.02;(c)=0.07;(d)=0.15Fig.7 The comparison of smooth degree with different initial weights(a)Control polygon;(b)=0.02;(c)=0.07;(d)=0.15

为验证所提出算法的有效性和可行性，以一例完整牙上颌(14颗牙数据样本)锥束CT断层扫描图像序列进行试验，实验数据参数见表1。提取后的切片轮廓用Mimics软件和本算法进行三维重建，并对重建后的模型质量进行对比。

为验证所提出算法的有效性及普遍适用性，对14例完整牙(每例28～32颗牙数据样本)锥束CT断层扫描图像序列进行试验，并与现有商用软件的实验结果进行比较，进行配对样本t检验，P＜0.05认为具有显著性差异。

表1 实例CT图像参数Tab.1 The parameters of the example CT images

3 结果

3.1 有效性实验

图8根据双数字牙位标记法［22］，选取16号牙作为研究对象。图8每行从左到右分别代表第34、39、44、49、54、59张牙齿切片轮廓的提取结果。图8(a)为Mimics软件提取的牙齿切片轮廓，可以看到，因为CT切片的多样性，同时由于单一阈值分割算法，难以准确地分割所有切片轮廓，导致部分切片轮廓线丢失;图8(b)是由Amira软件提取的牙齿切片轮廓，由切片44和切片59可以看到，此软件边界轮廓提取算法存在欠提取或者过提取的现象。图8(c)中的轮廓是本算法的实验结果，先进行轮廓增强，然后用收缩包围算法逼近增强的像素点，可以有效改善边界失真的状况。

图8 Mimics和Amira软件手工提取与本算法轮廓自动提取算法比较(每行自左至右分别为第34、39、44、49、54、59张牙齿切片轮廓提取结果)。(a)Mimics商业软件;(b)Amira商业软件果;(c)本算法Fig.8 The comparison of our results with those of Mimics and Amira software manual segmentation(Each line from the left to right respectively represents the results of extracted dental contours of 34th，39th，44th，49th，54th，59th figure).(a)Contour extracted with Mimics software;(b)Contour extracted with Amira software;(c)Contour extracted with our algorithm

图9 Mimics软件和本算法轮廓提取及三维重构对比。(a)Mimics分割结果;(b)Mimics三维重构;(c)本算法分割结果(简化后);(d)本算法三维重构Fig.9 The comparison of 3D reconstruction model between Mimics software and our algorithm.(a)Extracting the contours using Mimics;(b)3D reconstruction using Mimics;(c)Extracting the Contours using our algorithm(simplified);(d)3D reconstruction using our algorithm

提取后的切片轮廓用Mimics软件和本算法进行三维重建，并对重建后的模型质量进行对比。用一例完整牙上颌CT断层扫描图像序列进行试验(各参数见表1)，分别选取16号磨牙、11号切牙、13号尖牙，在进行轮廓提取后进行三维重建实验。由图9可以看出，基于Mimics软件和本算法在构建磨牙、尖牙和切牙重建时的三维模型质量相当。

3.2 效率对比

为验证本算法的有效性及普遍适用性，对14例完整牙(每例28～32颗牙数据样本)锥束CT断层的扫描图像序列进行试验，并得出统计数据，如表2所示。可以看出，Mimics和Amira手动分割每一例完整牙的单颗牙，平均用时在160～239 s之间;本自动分割算法用时不多于60 s，证明了本自动轮廓提取算法的高效性。

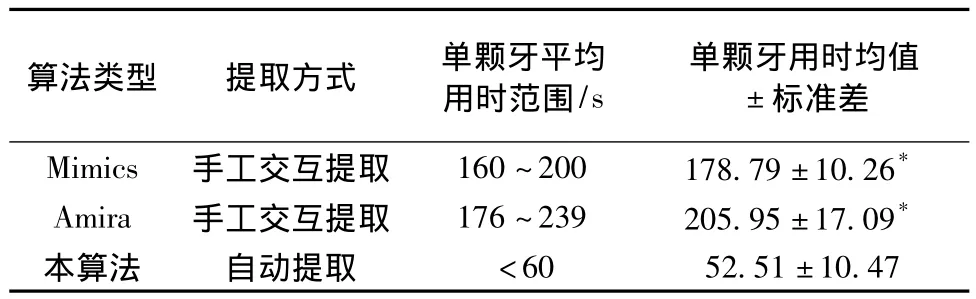
表2 本算法其与他算法的轮廓提取时间(s)统计Tab.2 The comparison of time(s)on extracting contours between our algorithm and others

为详细说明所提出算法的高效性，以一例完整牙上颌(14颗牙数据样本)锥束CT断层扫描图像序列进行试验(具体参数见表1)，实验结果如表3所示。Mimics和Amira手动分割单颗牙，用时分别为(177.14±5.78)s，(185.31±6.91)s;而本算法用时为(43.41±5.42)s。本研究所提出算法提取单颗牙轮廓平均用时为Mimics和Amira商业软件手工提取单颗牙平均用时的23%，很大程度上提高了轮廓提取的效率。

表3 Mimics和Amira软件与本算法轮廓提取用时(s)对比Tab.3 The comparison of time(s)between our algorithm and Mimics and Amira software

4 讨论和结论

针对现有的CT切片特征区轮廓提取技术难以实现轮廓自动分割的局限，提出一种基于启发式CT数据特征区的轮廓自动分割方法。目前，国内外现有的CT切片特征区轮廓提取主要采用手动层层提取的方法，不仅提取效率低，而且轮廓提取的精度受操作人员熟练程度的影响。本轮廓自动提取算法的提出，对减少目前医生仅仅凭经验进行轮廓分割的盲目性具有重要意义。

通过轮廓匹配映射实现初始轮廓的继承，从而实现已分割轮廓从上往下启发式自动传递。笔者将用于曲面细分的收缩包围算法用于特征区像素轮廓提取，不仅可以自动分割切片轮廓，而且解决了轮廓断裂的问题。本方法为CT数据特征区自动化分割提供了一种重要方法，为进一步改进现有的CT影像分割和三维重建算法提供了新思路。通过对CT切片数据进行自动轮廓提取实验，验证了算法的有效性实用性和高效性。由图9可知，Mimics软件和本算法在构建磨牙、尖牙和切牙三维模型上质量相差不大;但由表2可知，本算法提取单颗牙平均用时不到1 min，比传统方法提取单颗牙平均用时少很多，自动化程度和分割效率明显提高。

算法还有不足之处:由于不同人牙齿的形态差距很大，特别是存在突变区牙齿轮廓的提取，其拟合误差的大小还需要更多的实验数据来评估。另外，本算法仅在牙齿股骨头等CT数据上进行实验，并没有验证算法对人体其他部位轮廓相对复杂的CT数据模型的自动提取是否适用，具有一定的局限性。因此，在以后的实验中会更加关注这方面的研究。

本研究提出了一种基于启发式的CT轮廓自动提取方法，不仅保证了轮廓提取的精度，而且大大缩短了轮廓提取的时间。该方法为CT数据特征区自动化分割提供了一种有效的方法，对改进现有的CT影像数据自动分割和三维重建算法提供了新思路，对切片数据三维重构、特征提取、外科手术模拟和放射性治疗精确定位具有重要意义。

［1］孙涛，高东强.基于CT图像的个性化人骨三维建模方法［J］.机械设计与制造，2010，9(2):262－263.

［2］姜晓彤，罗立民.一种肺部肿瘤CT图像序列的自动分割方法［J］.中国图像图形学报，2003，9(8):1028 －1033.

［3］李想.CT图像的应用研究［D］.哈尔滨:哈尔滨工程大学，2004.

［4］Xu Chenyang，Prince JL.Snakes，shapes，and gradient vector flow［J］.IEEE TransactionsonImage Processing，1998，7(3):359－369.

［5］Shang Yanfeng，Xin Yang，Zhu Lei，et al.Region competition based active contourformedicalobjectextraction［J］.Computerized Medical Imaging and Graphics，2008，32(2):109－117.

［6］Yan Pingkun，Kassim AA.Segmentation of volumetric MRA images by using capillary active contour［J］.Medical Image Analysis，2006，10(3):317 －329.

［7］Ghanei A，Soltanian-Zadeh H，Windham JP.Segmentation of the hippocampus from brain MRI using deformable contours［J］.Computerized Medical Imaging and Graphics，1998，22(3):203－216.

［8］Cohen LD，Cohen I.Finite-element methods for active contour models and balloons for 2－D and 3－D images［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1993，15(11):1131－1147.

［9］侯晓丽，王博亮.基于Fast Marching Method的肝脏CT图像序列自动分割［J］.中国数字医学，2008，4(2):32－35.

［10］Jiao Pu，Justus R，Chin A，et al.Adaptive border marching algorithm:Automatic lung segmentation on chest CTimages［J］.Computerized Medical Imaging andGraphics，2008，32(6):452 －462.

［11］Zoroofi RA， Yoshinobu S， Toshihiko S，et al. Automated segmentation of acetabulum and femoral head from 3－D CT images［J］.IEEE Transactions on Information Technology in Biomedicine，2003，7(4):329 －343.

［12］Marcin C.Automatic liver segmentation from 2D CT images using an approximate contour model［J］.J Sign Process Syst，2014，74(10):151－174.

［13］张飞，樊瑜波.齿颌CT图像中牙的半自动分割方法［J］.生物医学工程学杂志，2007，24(1):15 －18.

［14］Dyn N， Leven D， Gregory JA. A 4-pointinterpolatory subdivision scheme for curve design［J］.Computer Aided Geometric Design，1987，4(4):257 －268.

［15］冈萨雷斯.数字图像处理学［M］.阮秋琦译.北京:电子工业出版社，2004.

［16］张毓晋.图像工程:图像处理和分析［M］.北京:清华大学出版社，2000.

［17］马涛，余春暄.数字图像处理在指针式指示表读数识别中的应用［J］.微计算机信息2004，7(20):116－117.

［18］Kobbelt LP，Vorsatz J，LabsikU，et al.A shrink wrapping approachto remeshing polygonal surfaces［J］.Computer Graphics Forum，1999，18(1):209 －237.

［19］Zhou Jinfang，Sherbrooke EC，Patrikalakis N.Computation of stationary points of distance functions［J］.Engineering with Computers，1993，9(4):231 －246.

［20］同长虹，刘经华.用权重系数法优选机械设计方案［J］.甘肃科技，2005，11(21):121 －123.

［21］尹庆水，万磊.Mimics软件在数字骨科的应用［J］.中国骨科临床与基础研究杂志，2010，2(2):137－139.

［22］李康军.虚拟牙齿矫正系统中的排牙算法研究与实现［D］.西安:西安科技大学，2009.