遗传算法在政府采购系统中的应用
李春梅,刘海雄
(青海大学 现代教育技术中心,青海 西宁 810016)
在政府采购业务[1-6]中,评审专家委员会是整个评标过程的关键,他们的结论将直接决定采购结果的公平、公正,因此评标专家的建立、管理是政府采购业务重要的环节之一。政府采购部门通过推荐、审批、考核等方式建立评审专家库。并在前期评标工作结束后,通过招投标监管机构、驻场监察员和招标单位对评标专家的工作态度、业务水平和公正合理性等进行评议打分,同时定期或不定期地组织参与招标投标的主体各方对评标等家进行测评,评议打分和测评的结果等作为年度考核管理的重要依据。为了确保政府采购行为的透明、公正、公平,文中通过改变传统手工的专家抽取过程,解决抽取方法不合理、抽取机会不均等、抽取与通知各自独立、人工干预多、保密性差、间隔时间过长等弊端,采用遗传算法来实现评标专家的抽取,以达到评审抽取的公正性和公平性的目的。
1 专家随机抽取的要求及抽取的条件
1.1 专家随机抽取的要求
评标专家抽取[2]的过程,首先授权给专家抽取的工作人员并凭证书登录系统,在监督人员的监督下进行现场抽取,整个抽取过程如图1所示。
1.2 专家随机抽取的条件设置
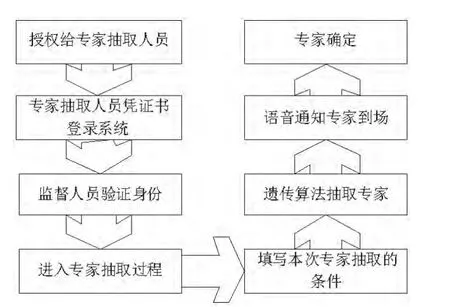
图1 评审专家抽取过程Fig.1 The extraction process of evaluation experts
按照每次评标的实际情况,要求抽取符合条件的评审专家进行参加评标活动。条件可包括:专业类别、每组人数、学历、职称和组数等。但有时因特殊需要,对专家条件需要更进步一步的限制:如1)同组专家成员要求:不能有多个专家是来自同一单位;2)学历要求:比如,10个专家中博士要有5人以上,硕士 3人以上;3)职称要求:职称必须为正高 6人以上,副高2人以上等。
2 遗传算法在专家随机抽取中应用
为了实现抽取过程的公正性和合理性,本论文将采用遗传算法对评标专家进行抽取。
2.1 遗传算法介绍
遗传算法[4,7]是在达尔文的“优胜劣汰”的生物进化理论得到启发,利用简单的编码技术和繁殖机制来表现复杂的现象,从而解决一些最优解等问题。其基本流程图如图2所示。本文中,对于流程图中的pt,pm,pc赋予了新的含义。Pt是在第i代染色体中,每次随机选择出10个染色体作为交叉和变异的个体;pc是将对选择后的染色体中依照其适应值查找出最高值和最低值,将最低值淘汰,将最高值取出将其出现的次数设置为2其余染色体不变,随机抽取出50%染色体,与剩下的染色体两两进行交叉计算;pm的值完全是视抽取评审专家的条件决定的,由1.2所述的1)2)3)3个特殊条件决定是否发生变异。
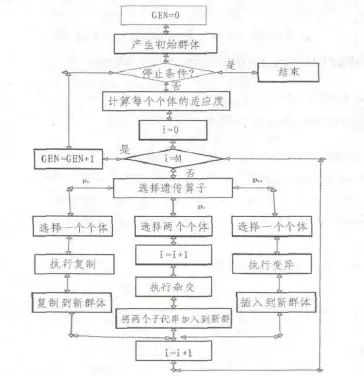
图2 遗传算法基本流程图Fig.2 The basic flow chart of genetic algorithm
2.2 遗传算法设计
2.2.1 基因和染色体的定义
我们假定一个专家个体就是一个染色体,若考虑到特殊要求,比如考虑专家的学历、职称以及来自同一单位的人数的限制等情况时,染色体可以定义为,领域编码+专家编码+单位编码+学历+职称。本论文中,所有基因的定义均采用十进制来表示。对领域编码是按照国家对学科领域的编码进行编码,用3位数来编码,如110为数学领域,150为化学领域,210为农学,220为林学等;专家编码采用3位领域数+3位专家在本领域中的编码共6位数来表示;专家所在单位用3位数来表示,如078表示青海大学;专家学历用1位数来表示,如1表示博士,2表示硕士,3表示本科;职称用1位数来表示,1表示正高,2表示副高,3表示讲师。例如430+430102+078+1+1是一个完整的染色体个体,表示材料学科的李某专家来自青海大学,学历为博士,职称为正高。在以上染色体定义中,领域编码和专家编码两个基因是决定染色体的主要基因,单位编码、学历和职称3个基因是决定染色体发生变异的主要基因,而发生变异的基因依然是专家编码。
2.2.2 适应度函数的定义
针对宿州市特色农产品销售管理系统,从功能需求分析、系统架构设计、 系统功能实现等三个方面对面向区域特色的农产品销售管理系统进行了系统化、科学化试验。目前,已经实现了基于移动端销售管理系统App的基本功能,但是在大数据分析和挖掘功能方面,仍需要作进一步的完善。
每个评审专家在入库时都需要经过资格评审和专业评审,并且每年均进行年度考核评审,因此各自具有一个评审分数,采用百分制,如98分。同时,参加过投标评审的专家均有投标方、被投标方和监督方三方从专业水平、评审态度和是否公正等三方面以百分制方式进行打分,这些也都成为每个评审专家的个人成绩。我们将入库时的打分标准和参加评标活动后对专家的打分标准一致化,将所有成绩的平均分作为这个专家的最后分数。在遗传算法中,将专家的最后分数除以 100 定义为该专家的影响因子 p(i),即 p(i)=avg(评审分数+年度考核分数+投标方打的分数+被投标方打的分数+监督方打的分数)/100。未参加过投标评审的专家,其影响因子是 p(i)=avg(评审分数+年度考核分数)/100;多次参加评审的专家其投标方打的分数、被评标方打的分数及监督方打的分数均为多次参加评审时多得分数的平均分。
2.2.3 种群的定义
我们假定本次评标所需的一组专家为一个种群。评审专家抽取之前,按照输入的评审专家领域条件的要求,把专家库所有该领域的专家抽取出来,然后在这些专家中按照输入的评审专家人数的要求,随机抽取出指定的人数,这个人数就是遗传算法的规模M,将这些随机抽取出来的专家进行数字化后形成了染色体定义格式的初始种群。在此基础上经过一系列的复制、杂交和变异最终产生符合条件的一组专家,将获得的最终目标种群,将染色体格式翻译成专家库中的记录形式、将本次专家信息进行保存记录并显示在输出设备上,然后进行语音通知,最终确定本次的评审专家。
2.3 遗传算法各算子的定义
2.3.1 选择算子的定义
选择是对那些适应值高的染色体进行选择,通过选择算子将种群中适应值高的染色体被选中到交配池中。适应值的计算按如下方法计算:
专家的适应值由3部分构成:专家入库时的资格考核成绩、专家每年的考核平均分、专家参加评标项目后由评标单位、被评标单位和监管单位进行的评分的平均分[8]。最终值为这三项分数的平均分,对于未参加过评标的专家的适应值是由(1)和(2)的平均分。按照定义的遗传算法的规模M,随机选择的初始群体,依照找出适应值最高和最低的评审专家,进行“优胜劣汰”,将分数最低的专家首先淘汰。
2.3.2 交叉算子
如:两个被选择的染色体为,包括5部分数据:领域编码,专家编码,单位编码,学历编码和职称编码。
1)430 430102 078 1 2 ,其适应值 p(1)=98/100
2)430 430088 078 1 2, 其适应值 p(2)=96/100
交叉计算的结果为:
3)430 430082 078 1 2, 其适应值 p(3)=94/100
4)430 430108 078 1 2, 其适应值 p(4)=99/100
计算结束后检查编码为108和082两位专家的第3、4、5部分数据以及适应度是否与原来库中的所在单位、学历和职称是否相同,若不同,则将其所在单位、学历和职称以及适应度修正为正确的信息。1)和2)交叉的结果最终是:
3)’430 430082 067 1 3 其适应值 p(3)为 98/100 4)’430 430108 067 2 2 其适应值 p(4)为 97/100
2.3.3 变异算子
变异是针对特殊要求而产生的计算。在文中,引发变异的条件是2.2中提及的1)2)3)3条特殊条件。个体是由专家编码决定的,而变异的基因是由3个条件决定,即,变异是由专家的单位编码、学历编码和职称编码决定的。因此,专家编码是决定遗传的主要基因,而单位编码、学历编码和职称编码作为变异时的主要基因,决定着染色体个体是否发生变异,但变异的发生点不是发生在单位编码、学历编码和职称编码上,而是发生在专家编码及对应的其他信息上。
比如,针对条件1),在上述交叉计算结束后产生的种群中,检查第3组数据是否有多组数据是相同的,即是否有多个专家均来自同一单位,若是,则要在第2组数据,即对专家编码进行变异操作,并将其他的响应信息也进行修改,以保证专家信息的一致性。计算过程如下:
检查 3)4)两个染色体,其第3部分数据均为 067,说明他们均来自青海师范大学,这不符合“专家不能来自同一单位”的条件,因此需发生变异。在3)4)两组数据中随机抽取一组数据进行变异计算。因为不论条件怎么变化,我们最终抽取的专家是由专家号来决定,因此,虽然发生变异的条件由“单位编码”来决定,但发生变异的基因依然是“专家编码”。假设,抽取3)组数据,变异发生在082这三位数中的任何一位,变异的候选值是专家编码中各位的最大数以内。假设,本领域专家编码最大为138,则发生变异时的规则时,若发生在第 1位,则由 0变为1,此时,第2位变为0,1,或 2,第3位变为 0,1,2,3,4,5,6,7,8,9;若发生在第 2 位或第 3 位,则由 8变为 0,1,2,3,4,5,6,7,9 均可。 总之,发生变异后的专家编码不能大于本领域中的最大专家编码。编码发生变异后,对应的单位号、学历和职称等其他信息也随着发生变化,以确保专家信息的正确性。因此,变异后的染色体为:5)430 430109 056 2 2。变异操作结束后,再检查其余染色体的单位是否满足条件,若不满足继续变异,直到满足条件为止。
同理,针对2)和3)特殊条件,采用此方法进行变异。
2.3.4 终止条件
当评审专家的3个特殊条件1)2)3)满足并且循环T次数达到300次时,循环终止。
3 实验数据分析
当条件中不要求学历和职称时,只要求专家领域为材料科学时,在筛选出材料科学领域所有专家的前提下,随机抽取出10名专家,作为初始群体,其个体的染色体表示及其适应值如表1所示。

表1 第0代群体Tab.1 The zeroth generation group
在上表的基础上进行一次选择计算之后,将适应值最高的个体在交配池中出现2次,而适应值最小的个体则被淘汰。杂交计算的结果如表2所示。
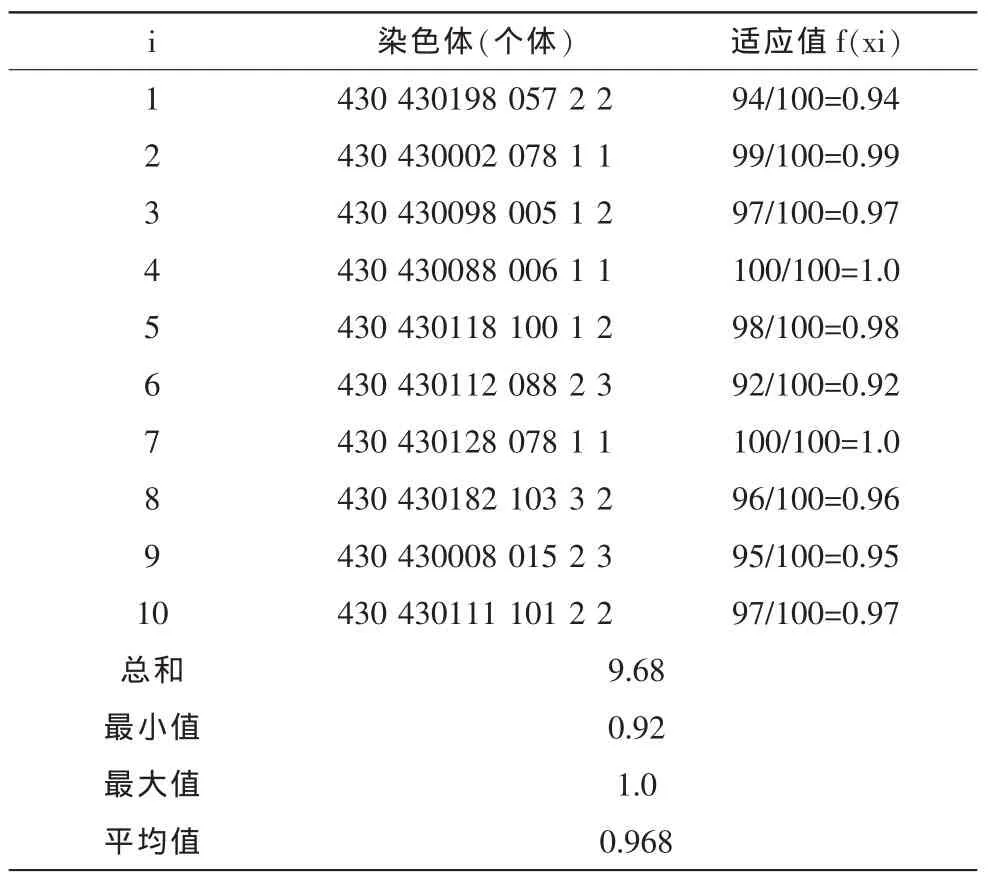
表2 第1代群体Tab.2 The first generation group
在表2中,依据特殊条件 1)2)3)依次进行变异,经过 T次的选择、交叉和变异,最终实现“优胜劣汰”,生成符合条件的10名评审专家的信息。通过交叉计算的结果,将“优”的个体被选入了交配池,“差”的个体被淘汰了,但是交叉计算的结果并不一定产生“更优”的个体。只是将每一代中相对“优”的个体生存下去,相对“差”的个体被淘汰。经过T次循环后得到相对“优”的个体“生存下来”,所有“劣”的个体均被淘汰。体现遗传算法的公正性、公平性和合理性。
4 结束语
文中采用遗传算法对评标项目的评审专家进行抽取,整个过程简单、方便,一方面比传统的手工抽取更具有随机性、科学性,另一方面整个抽取过程交给计算机去实现,减少人为干扰,体现了公平性、公正性。遗传算法不但实现了对评审专家的随机抽取,也实现了对投标单位的随机抽取。科学合理的进行优胜劣汰,使得电子化政府采购系统可以发挥更有效的作用。
[1]邢新岭,唐明.工程项目的招标专家抽取系统的设计[J].软件开发与设计,2013(8):33-35.XING Xin-ling,TANG Ming.Design of the bidding evaluation expert system[J].Software Development and Design,2013(8):33-35.
[2]牛勇,刘海雄.青海省政府采购专家管理系统中专家库的抽取方法 [J].青海大学学报:自然科学版,2008,26(4):27-31.NIU Yong,LIU Hai-xiong.Extractionm ethod of expert database in the expert managem ent system of Qinghai provincial government[J].Journal of Qinghai University:Nature Science,2008,26(4):27-31.
[3]童吉.高校设备采购专家抽取和语音通知系统的构建[J].实验技术与管理,2013,30(5):221-223.TONG Ji.Construction an expert-choosing and voice-notification system for equipment procurement in colleges and universities[J].Experimental Technology and Management,2013,30(5):221-223。
[4]杜浩.基于遗传算法的FMS调度问题研究[D].武汉:湖北工业大学,2014.
[5]王巍,刘云.铁路工程招标专家抽取系统设计[J].铁路计算机应用,2011,20(4):34-36.WANG Wei,LIU Yun.Design of experts extracting smart system in tender of railway construction[J].Railway Computer Application.2011,4.20(4):34-36.
[6]覃奕.评标专家系统设计[J].广西科学院学报,2014,30(1):1-4.Tang Yi.Designofthe Bidding Evaluation Expert System[J].Journal of Guangxi Academy of Sciences.2014,30(1):1-4
[7]宋骏豪.一种基于遗传算法的保险方案智能推荐方法[J].计算机与现代化,2013(215):80-83.SONG Jun-hao.An intelligent recommendation approach for insurance scheme based on genetic algorithm[J].Jisuanji Yu Xiandaihua,2013(215):80-83.
[8]周云端,何志勇,赵瑞国.基于遗传算法的加速度控制PID参数自整定研究[J].火箭推进,2012(4):68-71.ZHOU Yun-duan,HE Zhi-yong,ZHAO Rui-guo.Study on genetic algorithm based auto-tuning of acceleration control PID parameters[J].Journal of Rocket Propulsion,2012(4):68-71.

