基于星座点分布的TDM－OFDM自适应调制识别算法

程 聪

(上海大学通信与信息工程学院，上海200072)

1 引 言

在当今无线通信的应用中，有限的频谱资源与巨大用户容量需求之间的矛盾日渐突出，具有高频谱利用率的通信体制成为通信系统的重要研究方向。以高的频谱利用率为优势的正交频分复用(Orthogonal Frequency Division Multiplexing，OFDM)通信体制已成为现代数字通信系统的重要方式之一，但OFDM系统存在一个重要的缺陷:峰均功率比(PAPR)过高。为对抗OFDM系统中固有的PAPR问题，时分复用－正交频分复用(TDM－OFDM)系统通过将较长符号的逆傅里叶变换处理转换为对较短序列的处理，降低了PAPR处理方法的复杂度［1］。自适应调制解调技术是依据信道估计结果，根据各子载波信道条件的优劣，遵循一定的约束条件在各子载波或传输帧内切换使用不同的调制方式。将自适应调制解调技术应用到TDM－OFDM系统，可更充分利用信道资源，提高数据传输效率，使TDM－OFDM系统适用于移动快衰落传输环境［2］。在非协作通信环境中，如频谱监测、电子对抗和认知无线电等，接收端需对接收信号进行调制方式的识别，并利用得到的调制方式和调制参数信息进行解调译码。本文针对TDM－OFDM系统，研究调制方式识别算法。在TDM－OFDM系统，使用的调制方式包括四相相移键控(QPSK)和八相相幅调制(8PAH)。

目前针对OFDM信号子载波的调制方式的识别方法主要有如下几种［3－7］:文献［3］中提出了一种利用高阶累积量实现对多种调制信号进行识别的方法，通过选用不同阶累积量特征参数实现调制方式的识别;文献［4］中针对子载波为正交振幅调制(QAM)类调制方式的OFDM自适应调制系统，通过提取一种基于高阶混合矩的特征量达到盲识别的目的;文献［5］中针对子载波为相移键控(PSK)和QAM类调制的OFDM系统，采取联合高阶混合矩和高阶累积量分步识别的方法实现了对四种调制方式的识别;文献［6］中针对子载波为多进制数字相位调制(MPSK)信号的OFDM系统，提出了一种在载频估计基础上用减法聚类法重构星座图，通过统计聚类中心数目来确定调制方式的识别算法;文献［7］利用高阶累积量特征将OFDM信号中的空子载波与导频子载波滤除，然后利用减法聚类的方法判断子载波调制方式，识别的调制类型包括{QPSK，16QAM，64QAM}。上述方法针对OFDM系统的子载波使用限定的调制方式能够实现识别，但在识别本文研究的TDM－OFDM系统中的QPSK和8PAH时，却难以实现有效识别。因此，本文重点研究基于QPSK、8PAH作为子载波调制方式的 TDMOFDM自适应调制信号的识别方法，提出基于星座点分布统计特征的调制模式识别算法。

对于自适应调制解调系统，载波同步技术依赖于信号的调制方式，各数据帧中调制方式的改变会导致载波同步模块的锁相环频繁失锁，针对此问题，本文提出预置相位补偿方法解决解调失锁问题，以满足基于调制识别的自适应调制解调系统的工程应用需求。

2 系统模型与问题描述

TDM－OFDM信号的帧结构示意图如图1所示，每一个子载波的时分多址(TDMA)帧分为N个时隙，每个时隙包含Ns个符号。其中第1时隙为同步时隙，第2—5时隙为调制编码控制时隙，后续时隙都为用户数据时隙。同步时隙和调制编码控制时隙的调制方式不变，用户数据时隙采用自适应调制方式，调制方式包括 QPSK和8PAH。为了便于接收解调时进行精确的帧同步和样点同步，同步时隙采用m序列生成，将同步时隙设计为发送单频，并在单频尾部加入调制信号，用于发送m序列。调制编码控制时隙采用QPSK调制，信道编码采用交织、BCH码、加扰等方式，该时隙承载的信息包含一个TDMA帧内每个用户数据时隙的调制方式和编码方式。

图1 TDMA帧结构Fig．1 TDMA frame structure

在TDM－OFDM自适应调制解调系统中，解调器一般分为基带预处理、帧同步、快速傅立叶变换(FFT)、解译调制模式信息、解译信号负载部分等步骤。本文提出的算法针对该系统模型中特定调制方式的切换，采用基于星座点统计特征的调制识别方法得到调制模式信息，再据此对用户载荷部分解调译码。系统流程如图2所示。

在图2中，接收数据后，基带预处理模块通过数字下变频将中频信号转换为基带信号。帧同步模块用于确定TDMA帧的精确起点，其中包含两个阶段，首先通过延时相关累加功率检测粗测帧起始位置，然后利用m序列相关峰确定TDMA帧精确起点。另外，为了提高同步精度及减少由于频偏造成的信道间干扰(Inter－Carrier Interference，ICI)，利用同步时隙的单频信号进行频偏粗估计与纠正。完成帧同步后，FFT模块用于提取每个通道的基带I、Q路调制信号。完成FFT后，对调制模式进行识别，将得到的调制指示信息用于解译信号负载部分进行载波同步和译码。

图2 自适应调制解调算法流程图Fig．2 Improved demodulation algorithm for adaptive modulation system

3 基于星座点分布的调制模式识别和载波同步预补偿算法

3.1 基于星座点分布特征的调制模式识别算法

对调制方式进行快速准确的识别是本文研究系统的重要环节，本文提出基于星座点分布特征的区域统计法来解决这个问题。由图3可见，根据QPSK星座分布特性，在以坐标原点为中心的某个圆形区域内，该调制方式的数据星座点落点个数理论值应为零。而8PAH星座在某特定圆形区域内包含两个星座点，在一个时隙内该圆内的数据落点数目应该远远大于QPSK调制的落点数目。因此，可以通过点数统计选定一个经验阈值，将此阈值作为这两种调制方式的判别依据。

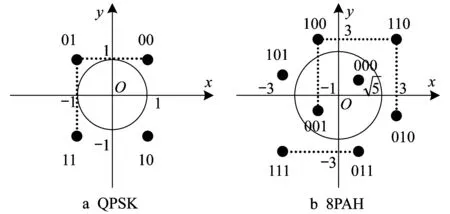
图3 调制星座图及圆形区域示意图Fig．3 Modulation constellation and circular area diagrams

对于上述圆形区域的选取实现过程如下:假设该时隙内的功率平均值为

Ns是一个时隙内的符号总数。把满足公式x2+y2=E/2的圆作为这个圆形区域的边界，即半径r=。假设在一个时隙内各星座点出现的概率相同，根据式(1)计算得到QPSK调制的时隙中E=2，则r=1;计算得到8PAH调制的时隙中E=10，则r=槡5。从图3可知QPSK星座图的圆形区域中无星座点分布，8PAH星座图的圆形区域中包含了两个星座点。因此，在相同符号数的前提下，采用这两种调制方式的数据在半径为的圆形区域中的星座点数目会有较明显的区别，可以此作为区分两者的依据。本文将在仿真部分对实际数据中的落点情况进行统计并确定阈值。

3.2 载波同步预补偿方法

载波同步模块包括自动增益控制和载波同步部分，主要完成相位捕获与剩余频偏跟踪。应用经典科斯塔斯(Costas)环［8－9］对信号载波同步时发现，算法对于8PAH的收敛相位与标准星座图相差π/4，该相位差导致调制方式切换时锁相环频繁失锁。因此，本文采用加入相位控制的Costas环实现载波同步，即根据调制模式识别结果，在调制方式切换时预置π/4的相位误差值，同步环结构图见图4。由此可补偿初相跳变，使锁相环平稳入锁。

假设输入信号可以表示为:

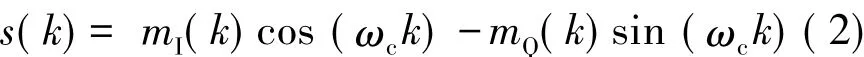
图4 加入相位控制的载波同步环结构框图Fig．4 Diagram of carrier synchronization loop with phase control

其中:mI(k)，mQ(k)分别为相互正交的I/Q路信号;ωc表示载波中心频率。图4中数控振荡器(NCO)产生跟踪载频，假设本振与输入信号的相位差为 Δθ，则可知:r1(k)=cos(ωck+Δθ)，r2(k)=sin(ωck+Δθ)。因此，当输入信号与NCO的两路输出混频后，可得到u1(k)和u2(k):

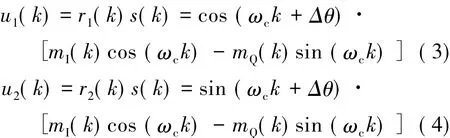
u1(k)和u2(k)中包含的高频分量经过低通滤波器滤除后，可得u3(k)和u4(k):

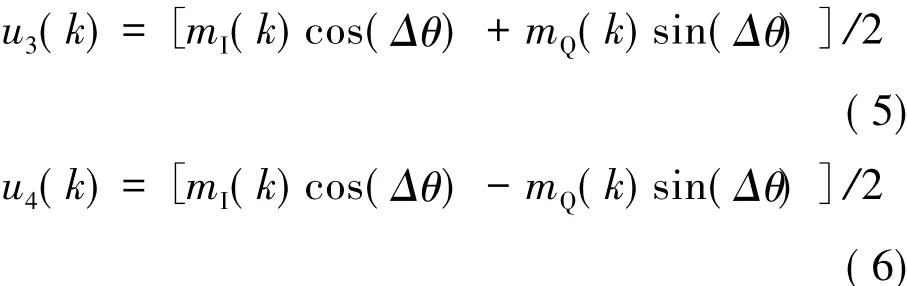
鉴相器即相位误差检测模块通过非线性变换估计载波相位误差，得到包含相位误差的函数:

式(7)中的误差信号u5( k)被送入环路滤波器，得到Δθ后对NCO中的本振频率进行校正，同时根据调制识别结果判别是否进行π/4相位预补偿，由此实现稳定入锁。

3.3 计算量和实现复杂度分析

本节着重分析本算法在计算复杂度方面的优势，这里将本文研究的利用调制方式识别得到调制模式信息的自适应调制解调系统，与另外一种在工程应用中使用的利用调制控制信息解译模块得到调制模式信息的调制解调系统进行比较，该系统对应的算法流程如图5所示。

图5 另一种自适应调制解调算法流程图Fig．5 Another demodulation algorithm for adaptive modulation system

在上述TDM－OFDM自适应调制系统的解调算法中，调制控制信息解译模块需要在FFT之后对调制控制时隙进行载波同步和信道译码来提取控制信息。其中载波同步原理见3．2部分，在每个TDMA帧中每个时隙内符号总数为Ns，控制时隙个数为4个，则实际计算中每帧需要做4×7Ns次乘法和4×7Ns次加法来完成载波同步。在信道译码模块中，需要对数据去扰码、解交织后，再对BCH码译码才能解译出调制控制信息。BCH译码计算复杂度较高，其译码算法一般包括硬判决代数译码、软判决最大似然算法、软判决格形译码等类型［10］。虽然近年来学者们不断简化和改进以上算法，在纠错能力、存储资源和译码速度上寻求折衷，但以迭代算法或查表法为代表的BCH译码算法皆有各自的瓶颈。迭代算法通常会带来接近于码长级数倍的计算量，查表法在码长较长或纠错位数较多时需要占用较大的存储资源来存放错误图样列表，并且需要优化的错误图样搜索算法。综上，该方法计算量是载波同步、去交织、解交织、BCH码译码等所有计算量的总和。

在本文3．1部分提出的调制模式识别模块中，首先根据式(1)计算平均功率，再根据实际数据星座点进行模式判断，因此在每个TDMA帧中只需要做Ns×4Ns次乘法、Ns×2Ns次减法即可完成对各时隙调制模式的识别。

通过对两个模块计算量的比较可知，调制信息的解译模块总体计算量超过本文提出的调制模式识别模块，而后者的算法复杂度却大大低于前者。在FPGA中实现本文算法时，只需要一个调制识别模块就可以实现对帧中所有时隙的识别，不需要额外添加对调制控制时隙的载波同步和译码模块，只占用较少的硬件存储空间。可见在软硬件实现的复杂度方面，本文算法明显更优。

下面针对仿真数据和实验结果，着重讨论调制模式识别和载波同步部分。

4 算法实现与分析

设定系统子载波数为16，一个TDMA帧包含的时隙数N=256，时隙内符号Ns=4 096，调制速率为 3．375 MB。

以信噪比为8dB的仿真数据为例，按照式(1)计算确定两种调制方式星座图中的圆形区域位置，如图6所示。

图6 仿真数据星座图和圆形区域图Fig．6 Constellation and circular area diagrams of simulation data

在8～20 dB各信噪比点下对两种调制方式的仿真数据分别计算E，并统计圈内半径r=的点数，可以得到统计曲线如图7所示，图7中星座点值较高的曲线为8PAH星座点落在圈内的点数分布，值较低的曲线为QPSK星座点落在圈内的点数分布。由图7中看到两种调制方式在圈内点数分布上有明显的区分，设定固定阈值S=350点作为两种调制方式的判决门限。根据此阈值对大量仿真数据进行调制模式识别，实验结果表明，该判决方法在信噪比(SNR)大于8 dB的条件下可正确区分两种调制模式。

实验中发现，根据调制模式识别结果对数据段进行载波同步时存在严重问题，即信号在不同调制方式切换时，会有一个重新入锁的过程。图8为调制方式切换时星座图的变化，可见当在不同时隙间调制方式不变时，锁相环工作稳定;而当调制方式切换时，锁相环会短暂失锁。

图7 QPSK、8PAH区域内点数Fig．7 Sum of QPSK and 8PAH constellation points within the circular area

图9 a为锁相环相位误差估计曲线，图9b为锁相环累计相位误差曲线，很明显在圆圈标示的范围内出现了失锁与重新入锁的过程，图9c是圆圈处的放大。

图8 调制方式转换时的星座图Fig．8 Constellations during conversion of the modulation mode

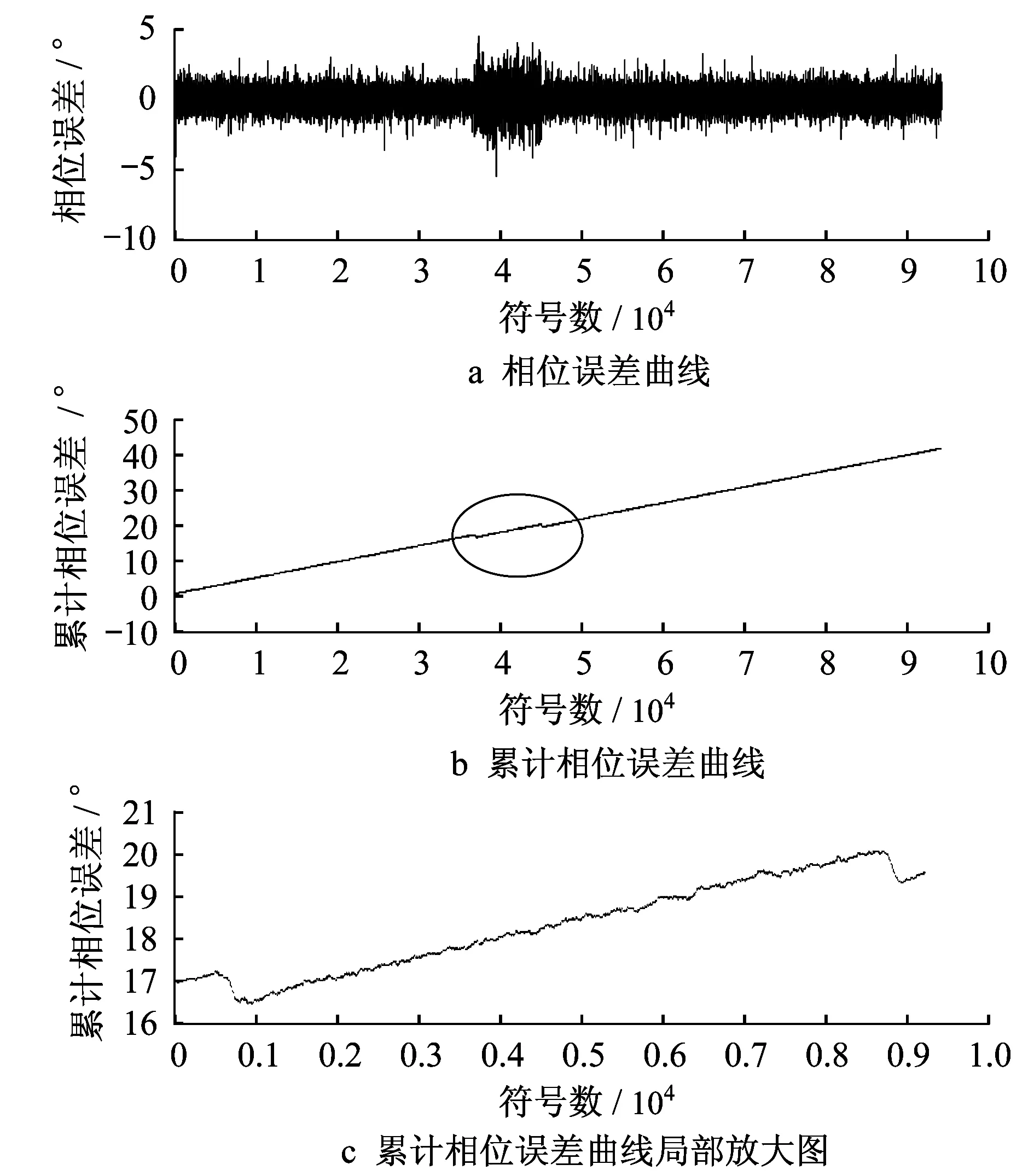
图9 未补偿相位的相位误差估计和累计相位误差曲线Fig．9 Phase error estimation curve and cumulative error curve without phase compensation

因此考虑是否是在不同调制方式切换时发生了初相跳变。为此，首先选取一个时隙做单时隙解调，在载波同步前增加非数据辅助的相位估计算法［11］，结果载波同步稳定入锁，说明确实是相位变化导致载波环失锁。比较前后时隙载波同步环初估相位差，发现接近π/4。于是在每一次调制方式突变时，累计误差上调π/4，发现消除了载波环失锁的问题，锁相环即可实现平稳切换。图10a为采用该算法后的锁相环相位误差估计曲线，图10b为锁相环累计相位误差曲线，图10c是对图10b的局部放大，仿真结果表明锁相环平稳入锁。

图10 相位补偿后的相位误差估计曲线和累计相位误差曲线Fig．10 Phase error estimation curve and cumulative error curve with phase compensation

5 结 论

本文针对子载波使用QPSK和8PAH两种调制方式的自适应调制TDM－OFDM系统，提出了基于星座点统计特征的调制识别方法。该方法利用QPSK和8PAH两种调制方式在一个特定区域中星座点分布特征的明显差异，统计得出识别阈值，通过该阈值实现对各时隙调制方式的识别。实验表明该方法在信噪比大于8dB时可以获得较好的识别正确率。本文把经典的Costas环应用于该特定系统的载波同步，但在实验中发现在时隙间调制方式切换时存在明显的初相跳变现象。于是在Costas环算法流程中加入相位控制模块，通过调制模式识别结果引导相位预补偿解决了该载波环失锁问题。仿真结果表明，本文算法可以很好地解决该TDM－OFDM自适应调制信号的解调问题，同时优化了解调处理流程，大幅降低了算法复杂度。

［1］ 吴玉成，伍丹，周强．适用于快衰落环境的 OFDM/TDM信道估计算法［J］．重庆大学学报，2011，34(2):64－68．WU Yucheng，WU Dan，ZHOU Qiang．Novel channel estimation algorithm for OFDM/TDM over fast fading channels［J］．Journal of Chongqing University，2011，34(2):64－68．

［2］ 杨迎新，宋桂景，贾岳．自适应OFDM调制解调［J］．无线电工程，2007，37(1):17－20．YANG Yingxin，SONG Guijing，JIA Yue．Adaptive modulation and demodulation in OFDM system［J］．Radio Engineering of China，2007，37(1):17－20．

［3］ 郭娟娟，尹洪东，姜璐，等．利用高阶累积量实现数字调制信号的识别［J］．通信技术，2014，47(11):1255－1260．GUO Juanjuan，YIN Hongdong，JIANG Lu，et al．Recognition of digital modulation signals via high-order cumulants［J］．Communications Technology，2014，47(11):1255－1260．

［4］ 安宁，李兵兵，黄敏．自适应OFDM系统子载波调制方式盲识别算法［J］．西北大学学报，2011，41(2):231－234．AN Ning，LI Bingbing，HUANG Min．Blind subcarrier modulation classification algorithm for adaptive OFDM system［J］．Journal of Northwest University，2011，41(2):231－234．

［5］ 朱洪波，张天骐，王志朝，等．基于高阶统计量的OFDM子载波调制识别算法［J］．光通信研究，2013(4):11－14．ZHU Hongbo，ZHANG Tianqi，WANG Zhichao，et al．A higher-order statistics-based modulation identification algorithm for OFDM subcarriers［J］．Study on Optical Communications，2013(4):11－14．

［6］ 赵春晖，杜宇．基于星座图的混合MPSK信号盲识别算法［J］．黑龙江大学工程学报，2012，3(4):70－75．ZHAO Chunhui，DU Yu．Blind recognition algorithm of mixed MPSK signals based on constellation diagram［J］．Journal of Engineering of Heilongjiang University，2012，3(4):70－75．

［7］ 刘明骞，李兵兵，赵雷．多径信道下OFDM信号子载波的调制方式识别新方法［J］．西安电子科技大学学报:自然科学版，2011，38(5):20－26．LIU Mingqian，LI Bingbing，ZHAO Lei．Modulation identification of the subcarriers of OFDM signals in multipath channel［J］．Journal of Xidian University:Nalural Science，2011，38(5):20－26．

［8］ Joh Hamkins，Simon Marvin K．Autonomous softwaredefined radio receivers for deep space applications［M］．New York:John Wiley ＆Sons Inc，2006:259－263．

［9］ Lee Kyung Ha，Jung Seung Chul．A novel digital lock detector for QPSK receiver［J］．IEEE Trans Commun，1998，46(6):20－23．

［10］ 朱建锋，安建平，王爱华．北斗导航信号BCH译码器中校正子辅助的列表译码算法［J］．电子与信息学报，2014，36(4):1013－1016．ZHU Jianfeng，AN Jianping，WANG Aihua．Syndromeassisted list decoding for BCH codes of china beidou navigation signal［J］．Journal of Electronics ＆Information Technology，2014，36(4):1013－1016．

［11］ Umberto Mengali，D ＇Andrea A．Synchronization techniques for digital receivers［M］．New York:Plenum Publishing Co．，1997:308－312．