2类优美图的冠的优美标号*

唐保祥 , 任 韩

(1.天水师范学院数学与统计学院，甘肃 天水 741001;2.华东师范大学数学系，上海 200062)



2类优美图的冠的优美标号*

唐保祥1, 任 韩2

(1.天水师范学院数学与统计学院，甘肃 天水 741001;2.华东师范大学数学系，上海 200062)

优美图是图论中重要的研究课题之一，有着广泛的应用价值和研究前景。但是目前仍然很难从理论上对一般图的优美性进行研究。马克杰猜想:所有优美图的冠都是优美图。这一猜想至今没有被证明或否定。对任何正整数m和n,用构造的方法给出了图I(1-Fm,4)和I(K1,1,1,n)的优美标号,从而证明了I(1-Fm,4)和I(K1,1,1,n)都是优美图。

优美图; 冠; 优美标号

图的优美标号是目前图论研究的一个热点问题[1-11],它的研究成果已经应用于密码理论、天文学、导弹控制、雷达、通讯网络寻址、数据库管理等方面[1-2]。文献[1]中给出了一个猜想：任意优美图的冠是优美图。这一猜想至今未被证明或否定。本文证明了两类优美图的冠是优美图。

1 相关概念

定义1[1]图G的每个顶点上都粘接r条悬挂边(r≥1的整数)得到的图,叫做G的r-冠。G的1-冠称为G的冠,记作I(G)。

定义2[1]设图G=(V,E),若存单射θ:V(G)→{0,1,2,…,|E(G)|},使得∀e=uv∈E(G), 由θ′(e)=|θ(u)-θ(v)|导出双射θ′:E(G)→{1,2,…,|E(G)|},则称图G是优美图,θ称为图G的一个优美标号,θ′称为由θ导出的边标号。

文献[1]中把顺序有一个公共顶点的m个4圈C4所形成的图记为Fm,4(如图1所示),Fm,4是优美图[1]。设V(Fm,4)={u0,u1,…,um,v1,v2,…,vn,w1,w2,…,wm},将顶点pi与图Fm,4的顶点vi和wi分别连接一条边(i=1,2,…,m)得到的图记为1-Fm,4(如图2所示)。

图1 Fm,4图Fig.1 Figure of Fm,4

图2 1-Fm,4图Fig.2 Figure of 1-Fm,4

2 主要结果及其证明

定理1 ∀m∈Z+,图1-Fm,4是优美图。

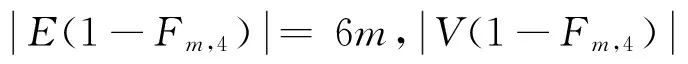
例如, 图1-F6,4的优美标号图3所示。

图3 图1-F6,4的优美标号Fig.3 Graceful labeling of graph 1-F6,4

令S1={θ(ui)|i=0,1,…,m},S2={θ(pi)|i=1,2,…,m},

S3={θ(vi)|i=1,2,…,m},S4={θ(wi)|i=1,2,…,m}。

因为S1∪S2={0,1,2,…,2m},minS3=2m+4,minS4=2m+1,max(S1∪S2)=2m-1, 所以Si∩Sj=Ø,i≠j。因此,映射θ:V(1-Fm,4)→{0,1,2,…,6m}是单射。

显然θ(v1)-θ(u0),θ(v1)-θ(p1),θ(v1)-θ(u1),θ(w1)-θ(u0),θ(w1)-θ(p1),θ(w1)-θ(u1),θ(v2)-θ(u1),θ(v2)-θ(p2),θ(v2)-θ(u2),θ(w2)-θ(u1),θ(w2)-θ(p2),θ(w2)-θ(u2),…,θ(vm)-θ(um-1),θ(vm)-θ(pm),θ(vm)-θ(um),θ(wm)-θ(um-1),θ(wm)-θ(pm),θ(wm)-θ(um)是首项为6m,尾项是1,公差是1的等差数列,所以θ′:E(1-Fm,4)→{1,2,…,6m}是双射,因此θ是图1-Fm,4的一个优美标号,图1-Fm,4是优美图。证毕。

定理2 ∀m∈Z+,图1-Fm,4的冠I(1-Fm,4)是优美图。

证明 根据图I(1-Fm,4)的定义,|V(I(1-Fm,4))|=8m+2,|E(1-Fm,4)|=10m+1。

设V(I(1-Fm,4))={u0,u1,…,um,v1,v2,…,vm,w1,w2,…,wm,p1,p2,…,pm,q1,q2,…,

qm,x1,x2,…,xm,y1,y2,…,ym,r0,r1,r2,…,rm},如图4所示。

图4 I(1-Fm,4)图Fig.4 Figure of I(1-Fm,4)

定义图I(1-Fm,4)顶点的标号θ如下:

θ(ui)=6i,i=0,1,…,m;θ(pi)=2+6(i-1),i=1,…,m;

θ(vi)=10m-1-4(i-1),i=1,2,…m;θ(wi)=10m-4(i-1),i=1,2,…m;

θ(qi)=10m-6-4(i-1),i=1,2,…m;θ(xi)=3+6(i-1),i=1,…,m;

θ(yi)=5+6(i-1),i=1,…,m;θ(ri)=10m+1-4i,i=0,1,…,m

例如, 图I(1-F6,4)的优美标号如图5所示。

图5 图I(1-Fm,4)的优美标号Fig.5 Graceful labeling of graph I(1-Fm,4)

令S1={θ(ui)|i=0,1,…,m},S2={θ(pi)|i=1,2,…,m},S3={θ(vi)|i=1,2,…,m},S4={θ(wi)|i=1,2,…,m},S5={θ(qi)|i=1,2,…,m},S6={θ(xi)|i=1,2,…,m},S7={θ(yi)|i=1,2,…,m},S8={θ(ri)|i=0,1,2,…,m},则maxS1=6m, maxS2=6(m-1)+2, minS3=6m+3,minS4=6m+4,minS5=6m-2, maxS6=6m-3,maxS7=6m-1,minS8=6m+1,所以Si∩Sj=Ø,i≠j,i,j∈{1,2,…,8}。因此，映射θ:V(I(1-Fm,4))→{0,1,2,…,10m+1}是单射。

因为θ(ri-1)-θ(ui-1),θ(wi)-θ(ui-1),θ(vi)-θ(ui-1),θ(wi)-θ(pi),θ(vi)-θ(pi),θ(vi)-θ(xi),θ(wi)-θ(yi),θ(wi)-θ(ui),θ(vi)-θ(ui),θ(qi)-θ(pi)(i=1,2,…,m),θ(rm)-θ(um),是首项为10m+1,尾项是1,公差是1的等差数列, 故θ′:E(I(1-Fm,4))→{1,2,…,10m+1}是双射,从而θ是图I(1-Fm,4)的一个优美标号,图I(1-Fm,4)是优美图。证毕。

文献[3]证明了：对任意正整数n，完全4部图K1,1,1,n是优美图。例如, 图K1,1,1,7的优美标号如图6所示。

图6 图K1,1,1,7的优美标号Fig.6 Graceful labeling of the graph K1,1,1,7

定理3 ∀n∈Z+,完全4部图K1,1,1,n的冠I(K1,1,1,n)是优美图。

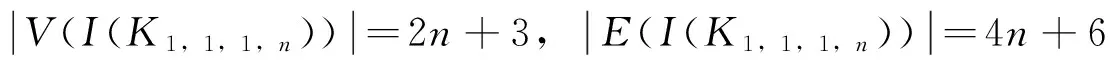
图7 图I(K1,1,1,n)Fig.7 Figure of I(K1,1,1,n)

定义图I(K1,1,1,n)顶点的标号θ如下:

θ(u0)=0;θ(u1)=n+1;θ(u3)=3n+6;

θ(x1)=n+2;θ(x2)=3n+5;θ(x3)=n+3;θ(vi)=3n+7+(i-1),i=1,2,…n;

θ(wi)=n+5+2(i-1),i=1,2,…n

例如, 图I(K1,1,1,7)的优美标号图8所示。

图8 图I(K1,1,1,7)的优美标号Fig.8 Graceful labeling of graph I(K1,1,1,7)

令S1={θ(vi)|i=0,1,…,n}∪{θ(x2),θ(u3)}={3n+5,3n+6,3n+7,…,4n+6},S2={θ(u1),θ(u2),θ(x1),θ(x3)}={0,n+1,n+2,n+3},S3={θ(wi)|i=1,2,…,n}={n+5,n+7,n+9,…,3n+3},则Si∩Sj=Ø,i≠j。因此,映射θ:V(I(1-Fm,4))→{0,1,2,…,10m+1}是单射。

因为θ(v1)-θ(u3),θ(v2)-θ(u3),…,θ(vn)-θ(u3),θ(u2)-θ(u1),θ(x1)-θ(u1),θ(vn)-θ(wn),θ(vn-1)-θ(wn-1),…,θ(v1)-θ(w1),θ(u3)-θ(x3),θ(x2)-θ(u2),θ(u3)-θ(u2),θ(vi)-θ(u2)(i=1,2,…,m),θ(u3)-θ(u1),θ(vi)-θ(u1)(i=1,2,…,m),是首项为1,尾项是4n+6,公差是1的等差数列, 故θ′:E(I(1-Fm,4))→{1,2,…,10m+1}是双射,从而θ是图I(K1,1,1,n)的一个优美标号,图I(K1,1,1,n)是优美图。证毕。

[1] 马克杰. 优美图[M]. 北京：北京大学出版社，1991.

[2] ALON N. Combinarorics, probability and computing [M]. Cambridge: Cambridge University Press, 1999, 150-236.

[3] 唐保祥. 关于K1,2,n和K1,1,1,n的优美性[J]. 上海师范大学学报：自然科学版, 1996, 24(4): 33-35.

[4] GALLIAN J A. A dynamic survey of graph labeling [J]. The Electronic Joumal of Combinatorics, 2013, 19, DS6:1-306.

[5] ZHOU X Q, YAO B, CHEN X E, et al. A proof to the odd-gracefulness of all lobsters [J]. Ars Combinatorial, 2012, 103: 13-18.

[6] KATHIESAN K M. Two classes of graceful graphs [J]. Ars Combinatorial, 2000, 22: 491-504.

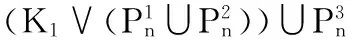
[8] 孙宗剑，黎贞崇，罗海鹏，等. 升降梯图L3m + n + 1的优美性[J]. 计算机应用研究, 2007, 24(12): 132-133.

[9] 容青, 熊冬春.P2r,b图的优美性[J]. 系统科学与数学, 2010, 30(5): 703-709 .

[10] 唐保祥，任韩.2类优美图[J]. 山东大学学报：理学版, 2010, 45(10): 45-48 .

[11] 唐保祥，任韩.3类特殊图的优美性[J]. 武汉大学学报：理学版, 2014, 60(6): 553-556 .

Graceful Labeling of the Corona for Two Kinds of Graceful Graphs

TANGBaoxiang1,RENHan2

(1. School of Mathematics and Statistics, Tianshui Normal University, Tianshui 741001, China;2. Department of Mathematics, East China Normal University, Shanghai 200062, China)

Graceful graph is one of the important research topics in graph theory with wide application and research prospects. But now it is still difficult to study the gracefulness of general graphs in theory. Ma Kejie conjecture is that all the coronas of graceful graph are graceful graphs. This conjecture has not been proved or denied. For any positive integersmandn, the constructor method gives graceful labeling ofI(1-Fm,4) andI(K1,1,1,n), thus prove thatI(1-Fm,4) andI(K1,1,1,n) are graceful graphs.

graceful graph; corona; graceful labeling

10.13471/j.cnki.acta.snus.2015.05.006

2015-01-24

国家自然科学基金资助项目(11171114)

唐保祥(1961年生)，男；研究方向：图论和组合数学;E-mail: tbx0618@sina.com

O157.5

A

0529-6579(2015)05-0024-04