强太赫兹激光作用下量子阱中载流子量子态的变化特征
王伟杨,吴 波,常 山,吕 岿,许 磊
(上饶师范学院 物理与电子信息学院,江西上饶334001)
强太赫兹激光作用下量子阱中载流子量子态的变化特征
王伟杨,吴 波,常 山,吕 岿,许 磊
(上饶师范学院 物理与电子信息学院,江西上饶334001)
利用Kramers-Henneberger平移变换法和分析转移矩阵方法,研究了强太赫兹激光作用下有限深矩形量子阱体系载流子量子态的变化特征。结果表明,电子能级和量子态(或积分几率)随电场强度的增大或辐射频率的减小而增大,势阱宽度越小量子态和电子能级受辐射场的影响越显著。当电场强度逐渐增大或辐射频率逐渐减小,单势阱量子阱将先转变成双势阱量子阱,然后转变成半导体体材料。最后,讨论了量子态变化特征的物理本质。
强太赫兹激光;量子态;量子阱;分析转移矩阵方法;激光缀饰势
太赫兹(1012Hz 或THz)科学科技被公认为是21 世纪电子和信息领域的重大科学问题和高新技术并受到世界各国的高度关注[1],但是太赫兹科学技术中还存在许多重大科学难题亟待解决,其应用也在不断的研究开发之中。随着超快光电子技术和低尺度半导体技术的发展(高功率、调频、线性极化太赫兹激光源的真空电场强度已达到100 kV/cm),太赫兹科学技术在研究半导体及低维体系物理特性等领域的应用越来越广泛[2]。特别是,强太赫兹激光辐照下低维半导体体系光学特性的研究引起了国内外科学家的高度关注[3-5],此时:(1)低维半导体体系受激载流子的动量和能量弛豫时间τ均在皮秒量级[6]并满足条件ωτ>1,强太赫兹激光将强烈修正体系受激载流子的动量和能量弛豫过程;(2)低维半导体体系的限制势[7-8]和态密度[9]被强太赫兹激光有效调制,以及太赫兹光子与体系元激发的能量具有相同数量级,体系将进入能带内的非线性区域。因此,强太赫兹激光辐照下低维半导体体系的光学性质将呈现出许多新颖的物理特性,并将丰富强外场作用下低维半导体体系载流子运动状态的知识。
在半导体器件领域,掌握强外场作用下低维半导体系统的电学和光学性质是设计半导体器件的基础。众所周知,量子阱的结构参数(势阱宽度、势阱形状以及势阱深度)对体系的电学和光学性质有重要的影响,所以强太赫兹激光辐照下量子阱体系的电学和光学性质将受到体系的结构参数和外场条件(电场强度和辐射频率)的共同影响。同时,强太赫兹激光辐照下量子阱载流子的量子态变化特征在研究调控量子阱激光[10]、共振隧穿效应[11],浅能级杂质态[12]、子带能级间跃迁[13]以及带间辐射复合[14]等具有重要作用。因此,强太赫兹激光辐照下量子阱载流子量子态变化特征的研究,不但可揭示体系非线性光学性质的物理本质,而且还将为设计半导体光电子器件提供理论支持。对于有限深矩形量子阱,E.C.Niculescu等利用Kramers-Henneberger (KH) 平移变换法[15]研究了强激光辐照下有限深矩形量子阱中浅能级杂质态密度的变化特征,他们首次得到了当激光缀饰参数α0≤L/2时(L量子阱势阱宽度), 有限深矩形量子阱的缀饰限制势,结果表明强激光可有效调制量子阱的限制势,这对浅能级杂质态密度产生重要影响[7]。随后,F. M. S. Lima等利用相同的方法进一步研究了强激光作用下有限深矩形量子阱的电学和光学特性,推导出了量子阱普适的缀饰限制势解析表达式,当激光缀饰参数α0>L/2时研究发现量子阱体系具有以下新颖效应[8]:(1)量子阱的单势阱转变成双势阱;(2)量子阱的电子束缚能级随α0增大而合并的效应为光学泵浦调控量子阱激光的粒子数反转提供了新的可能途径;(3)仅在量子阱势阱材料层中才能产生可调控的共振态。近几年来,科学家虽然利用KH平移变换法对强激光辐照下有限深矩形量子阱[16-17]、量子点[18]和抛物线形量子阱[19]的线性与非线性光学性质进行了大量研究,但是强太赫兹激光作用下有限深矩形量子阱中载流子的量子态随辐射电场强度和辐射频率的变化规律,以及外场条件(电场强度和辐射频率)和结构参数(势阱宽度和势阱深度)对量子阱体系量子态的调控效应还有待研究。
因此,本论文将对强太赫兹激光辐照下有限深矩形量子阱载流子量子态的变化特征展开研究,揭示出体系载流子量子态随结构参数和外场条件的变化规律,为设计半导体光电子器件提供理论支持。
1 理论方法

(1.1)

图1 I型量子阱导带底和价带顶的能带示意图

(1.2a)
其中
(1.2b)
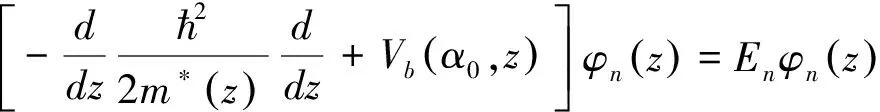
(1.3)

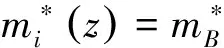

(1.4a)
(1.4b)

(1.4c)
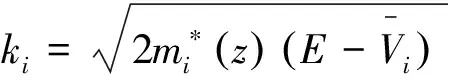
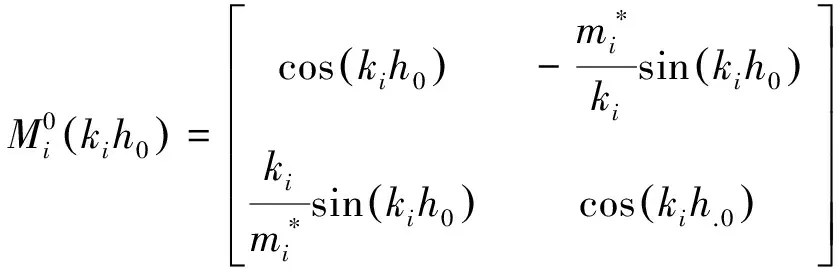
(1.5a)
和

(1.5b)
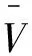
(1.6)


(1.7a)
(1.7b)
因此,综合式(1.4)—式(1.7),可得
(1.8)
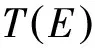
(1.9)
最后,电子波函数在量子阱体系的左右两端还满足第一类边界条件,即
(1.10)
因此,利用分析转移矩阵方法和式(1.8)—式(1.10)原则上可获得量子阱体系任意限制势的电子包络波函数和子带能级,在此基础上我们可揭示出强太赫兹激光作用下有限深矩形量子阱电子量子态随外场条件和结构参数的变化规律。同理,我们可获得强太赫兹激光作用下量子阱体系中空穴量子态的变化特征。
2 结果与讨论
量子阱AlxGa1-xAs/GaAs/AlxGa1-xAs体系在半导体光电子器件有着广泛的应用,所以本论文将以该体系为例进行数值计算。在量子阱AlxGa1-xAs/GaAs/AlxGa1-xAs体系中,窄禁带半导体GaAs为势阱材料A层,宽禁带半导体AlxGa1-xAs为势垒材料B层。由于在T=300 K时GaAs晶体与AlAs晶体的晶格失配度非常小,仅有0.14%,所以GaAs晶体与AlxGa1-xAs化合物晶体之间的晶格失配效应将变的微乎其微。因此,本论文将不考虑量子阱AlxGa1-xAs/GaAs/AlxGa1-xAs体系的晶格失配应变和应力等问题。量子阱体系势垒材料AlxGa1-xAs化合物半导体中Al元素的摩尔分数x取值在0~1之间:(1)当0

表1 量子阱体系材料的基本参数[22]
*a)T=300K时的禁带带隙;*b)B代表AlxGa1-xAs材料,A代表GaAs材料
当有限深矩形量子阱的势阱层具有不同宽度时,激光缀饰限制势Vb(α0,z)随辐射电场F0和辐射频率f的变化规律如图2所示。根据图2,我们可得到以下有趣的物理图像:(1)当辐射电场F0在0~F0pkV/cm(图(a)F0p=6.77和图(b)F0p=13.54)或辐射频率f在fp~10 THz(图(c)fp=3.65, 图(d)fp=2.58)区间时,激光缀饰量子阱的势阱层有效宽度L在 dA-2α0(势阱底部) ~dA+2α0(势阱顶部)区间连续变化,即能级En≤V0/2(En>V0/2)的电子态的有效势阱宽度L< dA(L> dA),激光对量子阱限制势的修正效应随辐射电场F0(辐射频率f)的增大而增强(减弱)。(2)当辐射电场F0在F0p~200 kV/cm或辐射频率f在0.1~fpTHz时,由于反余弦限制势函数的叠加效应,在势阱层-α0+dA/2~α0-dA/2区域内形成了对称的势垒峰,即形成双势阱的量子阱。同时,势垒峰的宽度为2α0-dA并随辐射电场F0(辐射频率f)的增大而增大(减小),势垒峰的极大值为Vtop(α0)=(2V0/π)arcos[dA/(2α0)]并位于量子阱势阱层的中心位置(z=0),势垒峰的极小值为Vmin(α0)=(V0/π)arcos(dA/α0-1)并位于势阱层z=-α0+dA/2和z=α0-dA/2处。(3)当电场强度F0≥200 kV/cm和辐射频率f~ 0.1 THz时,势阱层中的势垒峰趋于V0,这表明有限深矩形量子阱在强太赫兹激光作用下将转变成半导体体材料。(4)量子阱的势阱层宽度dA越小,激光对量子阱限制势的修正效应越显著,这表明势阱宽度与外场条件对缀饰限制势存在竞争关系。此外,由于激光缀饰参数α0=eF0/(m*ω2)与辐射电场F0(辐射频率f)成正比(反比),所以上述关于量子阱缀饰限制势的结果与E.C.Niculescu等[7]和F. M. S. Lima等[8]的强激光对量子阱限制势的修正效应随α0增大而增强的结论相符。
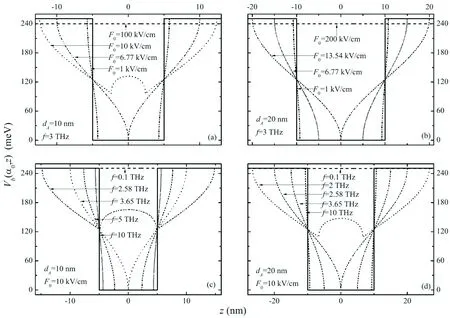
图2 有限深矩形量子阱的激光缀饰限制势Vb(α0,z)随电场强度F0和辐射频率f的变化规律,实线表示无强太赫兹激光辐照时的量子阱限制势Vb(z)
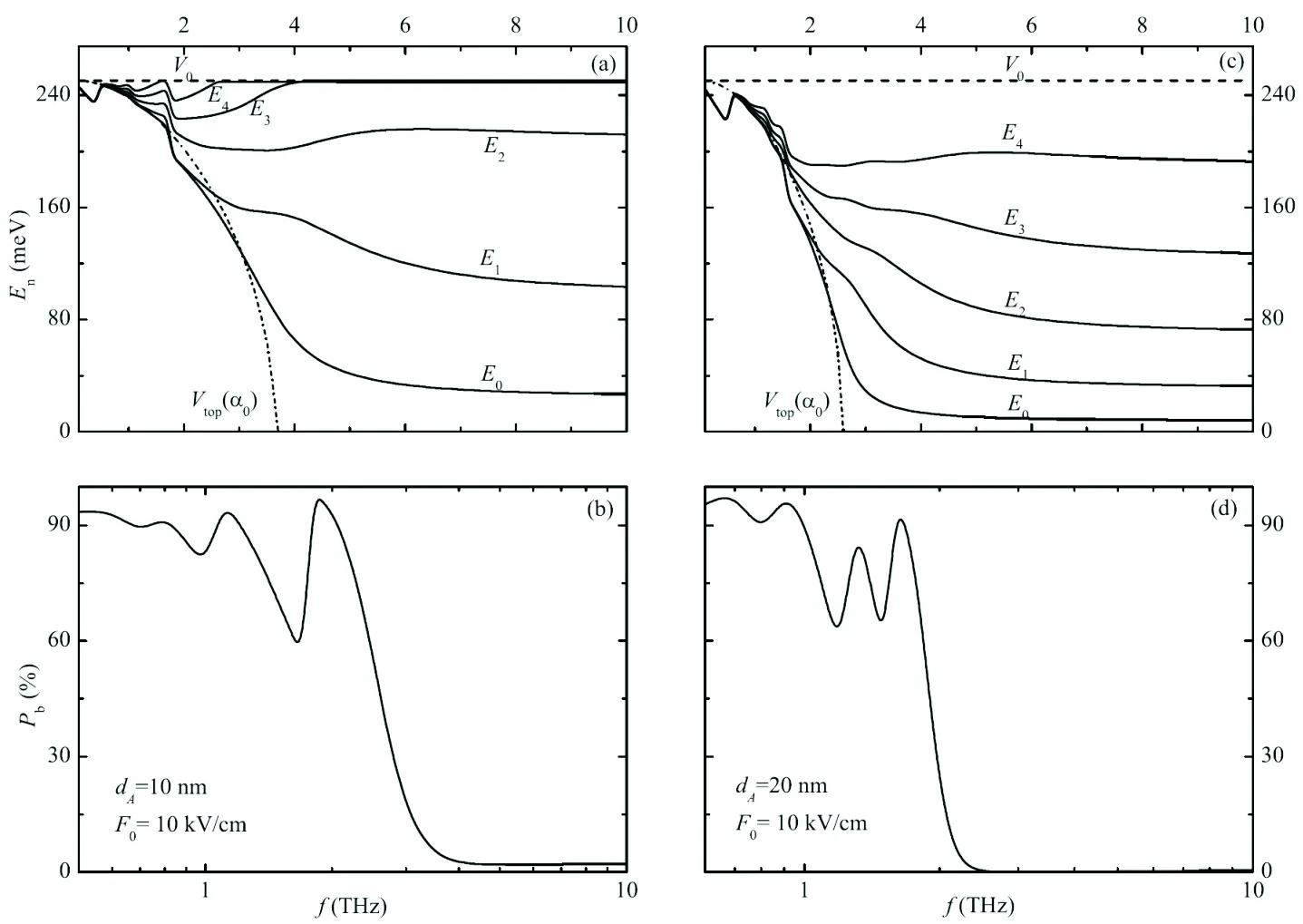
量子阱的量子隧穿效应是半导体纳米电子和光电子器件的物理基础。为此,引入量子阱势阱层基态电子波函数对势垒层的渗透效应,即渗入量子阱势垒层基态电子波函数的积分几率Pb[22]:
其中φ0(z)为量子阱势阱层导带电子的子带基态波函数,E0为相应的电子基态能级。图3和图4显示了当量子阱的势阱层具有不同的宽度dA时,并固定辐射频率f或辐射电场F0,辐射电场F0或辐射频率对电子能级En(n=0,1,2,3,4)和积分几率Pb的影响。由图3和图4,我们可得到以下量子态新颖的物理特征:(1)当辐射电场F0或辐射频率f比较小时,即0≤F0 图3 激光缀饰量子阱的电子能级En和积分几率Pb随辐射电场强度F0的变化规律,虚线和点虚线分别表示量子阱的带阶V0和势垒峰的极大值Vtop(α0) 图4 激光缀饰量子阱的电子能级En和积分几率Pb随辐射频率f的变化规律,虚线和点虚线分别 综上所述,有限深矩形量子阱AlxGa1-xAs/GaAs/AlxGa1-xAs体系在强太赫兹激光作用下,辐射场可有效修正量子阱的限制势形状和势阱宽度,所以强外场可调控体系的电子能级和积分几率(或量子态)。由于量子阱体系的量子态和电子能级受体系的结构参数(势阱形状、势阱宽度以及势阱深度)的影响[22],所以量子阱体系的电子能级和量子态将受到体系的结构参数和外场条件的共同影响,两者形成相互协助和相互竞争的关系。一般地,半导体电子和光电子器件的结构参数是确定的,所以我们的结论对利用强太赫兹激光有效调控量子阱电子和光电子器件的物理特性提供了坚实的物理基础。 本论文利用KH平移变换法和分析转移矩阵方法研究了强太赫兹激光作用下,有限深量子阱AlxGa1-xAs/GaAs/AlxGa1-xAs体系的电子能级和积分几率(或量子态)随外场条件的变化规律,研究表明:(1)电子能级和量子态随辐射电场和辐射频率的变化呈现显著的非线性效应; (2)随着辐射强度的增强和辐射频率的减小,体系结构将发生如下演化:单势阱量子阱先演化成双势阱量子阱,然后再演化成半导体体材料;(3)势阱宽度越小,辐射场对量子阱电子能级和量子态的修正效应越显著,即量子阱体系的量子态和电子能级受到外场条件和结构参数的共同影响,两者相互竞争。因此,强太赫兹激光作用下量子阱体系量子态的变化特征,为设计强外场调控的半导体电子和光电子器件提供了理论依据。 [1]Ferguson B, Zhang X C. Materials for terahertz science and technology[J]. Nature Materials,2002,(1): 26-33. [2]Lee Y S. Principles of Terahertz Science and Technology[M]. New York: Springer, 2009. [3]Brandi H S, Latgé A, Oliveira L E. Laser effects on donor states in low-dimensional semiconductor heterostructures[J]. Phys Rev B,2002,70(15): 153303-153309. [4]Lu L L, Xie W F, Hassanabadi H, et al. The effect of intense laser field on the Electronic Raman Scattering of shallow donor impurities in quantum dots[J]. Superlattices Microstruct. 2011,50(5):501-510 [5]Niculescu E C, Cristea M, Radu A. Laser-dressed donor states in a CdS/SiO2spherical nanodot under applied electric fields[J]. Superlattices Microstruct, 2014,69:65-75 [6]Xu W, Zhang C. Resonant absorption of terahertz electromagnetic waves by heated electrons in AlGaAs/GaAs heterostructures[J]. Appl Phys Lett, 1996, 68(23): 3305-3308. [7]Niculescu E C, Burileanu L M, Radu A. Density of impurity states of shallow donors in a quantum well under intense laser field[J]. Superlattices Microstruct, 2008,44(2):173-182. [8]Lima F M S, Amato M A, Nunes O A C, et al. Unexpected transition from single to double quantum well potential induced by intense laser fields in a semiconductor quantum well[J]. J Appl Phys, 2009, 105(12):123111- 123117. [9]Lima C P, Lima F M S, Fonseca A L A, et al. Magnetic field effect on the laser-driven density of states for electrons in a cylindrical quantum wire: transition from one-dimensional to zero-dimensional behavior [J]. New J Phys,2011,13:073005-073019. [10]Gerck E, Miranda L C. Quantum well lasers tunable by long wavelength radiation[J]. Appl Phys Lett, 1984, 44(9):837-839. [11]Zhang C. Resonant tunneling and bistability in a double barrier structure under an intense terahertz laser[J]. Appl Phys Lett. 2001,78(26):4187-4189. [12]Sari H, Kasapoglu E, Sokmen I, et al. Intense field effects on shallow donor impurities in graded quantum wells[J]. Semicond Sci Technol,2003,18(6):470-474. [13]Kasapoglu E, Sari H, Yesilgul U, et al. The effect of intense laser field on the photoionization cross-section and binding energy of shallow donor impurities in graded quantum-well wire under an electric field[J]. J Phys Condens Matter, 2006,18(27):6263-6271. [14]Xu W. Optical absorption by a semiconductor in the presence of intense radiation fields[J]. Appl Phys Lett, 2006, 89(17):171107-171109. [15]Henneberger W C. Perturbation method for atoms in intense light beams[J]. Phys Rev Letts, 1968,21(12): 838-841. [16]Ungan F, Yesilgul U,akirolu S, et al. Effects of an intense, high-frequency laser field on the intersubband transitions and impurity binding energy in semiconductor quantum wells[J]. Phys Lett A, 2010,374(29): 2980-2984. [17]Yesilgul U, Ungan F, Kasapoglu E, et al. Effects of an intense, high-frequency laser field on the binding energy of excitons confined in a GaInNAs/GaAs quantum well[J]. Physica B, 2012,407(3):528-532. [18]González-Santander C, Apostolova T, Domínguez-Adame F. Binding energy of hydrogenic impurities in quantum dots under intense laser radiation[J]. J Phys Condens Matter,2013,25(33):335802-335806. [19]Yesilgul U, Ungan F, Sakiroglu S, et al. Effect of intense high-frequency laser field on the linear and nonlinear intersubband optical absorption coefficients and refractive index changes in a parabolic quantum well under the applied electric field[J]. J Lumin,2014,145: 379-386. [20]Suzuki M, Transfer-matrix method and Monte Carlo simulation in quantum spin systems[J]. Phys Rev B, 1985,31(5):2957-2965. [21]Chen B, Lazzouni M, Ram-Mohan L R.Diagonal representation for the transfer-matrix method for obtaining electronic energy levels in layered semiconductor heterostructures[J]. Phys Rev B, 1992,45(3):1204-1212. [22]Bastard G. Wave mechanics applied to semiconductor heterostructures[M]. Paris:Springer,1990 The Variations Characteristics of Carrier Quantum States in Quantum Well in the Presence of Intense Terahertz Laser Fields WANG Wei-yang, WU Bo, CHANG Shan, LV Kui, XU Lei (School of Physics and Electronics Information,Shangro Normal University, Shangrao Jiangxi 334001, China) Within the Kramers-Henneberger translation transformation and the analytical transfer matrix methods, the variations characteristics of carrier quantum states is analyzed theoretically in a finite rectangular quantum well under intense terahertz laser fields. The results show that the electronic energy levels and quantum states(or integrated probability) increase with increasing radiation intensity or decreasing radiation frequency gradually, the effects of radiaiton field on these quantum states are more significance at smaller width of potential well. When the radiation becomes intense or the radiaiton frequency becomes low, firstly the single quantum well potential transits into double quantum well potential, and then such double quantum well transits into semiconductor. Finally, the physical reasons behind these finding are discussed. intense terahertz laser field; quantum state; quantum well; analytical transfer matrix method; laser-dressed potential 2015-10-13;修改日期:2015-11-10 国家自然科学基金 (11404214;1455015);江西省教育厅基金(KJLD12046;GJJ13707);上饶师院基金 (201411) 王伟杨(1982-),男,江西南昌人,讲师,博士,主要从事强外场作用下半导体及低维体系磁光电效应的研究。 E-mail: wywang2014@sina.cn O482.3 A 1004-2237(2015)06-0033-08 10.3969/j.issn.1004-2237.2015.06.007
3 结论

