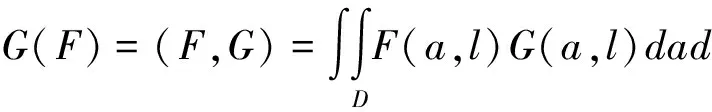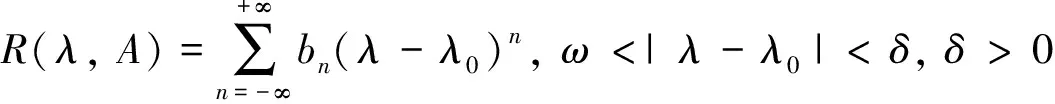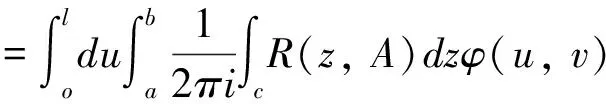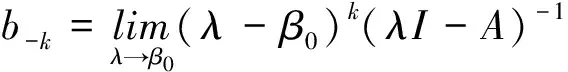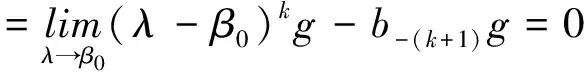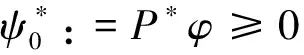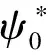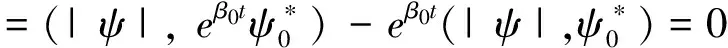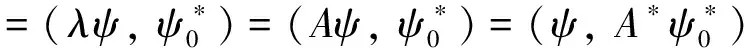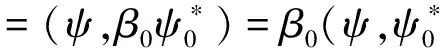细菌种群中一类迁移算子的占优本征值问题
王胜华, 潘世富
(1.上饶师范学院数学与计算机科学学院,江西上饶334001; 2.南昌大学数学系,江西南昌300031))
细菌种群中一类迁移算子的占优本征值问题
王胜华1, 潘世富2
(1.上饶师范学院数学与计算机科学学院,江西上饶334001; 2.南昌大学数学系,江西南昌300031))
在L2空间上,研究了一类具增生的细菌种群中具一般边界条件的迁移方程,得到了这类方程相应的迁移算子的占优本征值存在性等结果。
细菌种群;一般边界条件;迁移方程;迁移算子;占优本征值
1 引言
本文研究了以下一类具增生的细菌种群中迁移方程:
(1.1)
其中ψ=ψ(u,v,t)表示关于细菌的成熟度u(0 (1.2) 其中α,p≥0表示每一能有丝分解子细菌的平均数,p=1时保证了细菌通量的连续性,正核k=k(v,v')表示母体细菌v'和它的子细菌v间成熟速率的相互关系,并满足标准化条件 (1.3) 本文关注更 一般的生物规律,即在数学上表为更一般的边界条件: ψ(0,v,t)=Kψ(1,v,t) (1.4) 其中K表示边界空间上的有界线性算子。关于这类具增生的细菌种群中的迁移方程是由M.Rotenberg在文献[1]中提出来的,之后对该模型有许多研究工作(部分见文献[2-7])。最近,文献[6,7]在L1空间研究了这类模型,在边界条件α=0和边界算子为可容许算子[5,6]的情况下,得到了该模型相应的迁移算子产生不可约正C0半群,并讨论该迁移算子的谱和迁移方程解的渐近行为等。但是对边界条件(1.2)中αp≠0时的边界算子不是可容许算子,我们得到了该模型相应的迁移算子的谱分析和迁移方程解的渐近行为等结果。本文在L2空间得到了这类模型相应的迁移算子的占优本征值存在性等结果。 本节主要给出一些本文需要的空间和算子以及相关的结果。设 X=L2(D,dudv),D=(0,1)×(a,b)=I×J,(0≤a 它们分别按范数 和 构成的Banach空间。引进边界空间和范数分别为 Xi=L2(Γi,dv),i=1,2;Γ1={(0,v):v∈J};Γ2={(v,v):l∈J}. 引理2.1[5]若ψ∈W,则ψ|Γ1∈X1的充要条件为ψ|Γ2∈X2.其中 ψ|Γ1=ψ(0,v),ψ|Γ2=ψ(v,v). 定义迁移算子A为: 其中σ(.,.)∈L∞,边界算子K为: K:X2→X1,Kψ|Γ2=ψ|Γ1. 对φ∈X,λ∈C,ψ∈D(A),考虑方程 (λ-A)ψ=φ. (2.1) 则∀λ,Reλ>-σ(σ=essinf{σ(u,v) ∈I×J}),方程 (2.1)可形式地解为: (2.2) 取u=a,则(2.2)式为: (2.3) 根据(2.2)式和(2.3)式引进如下算子: 则由Hölder不等式知以上算子都是有界的,且 并在X+(X的正锥)上Bλ、Dλ、Eλ和Fλ都为正算子。从而(2.3)式和(2.2)式分别为: ψ|Γ2=BλKψ|Γ2+Eλφ. (2.4) ψ=DλKψ|Γ2+Fλφ. (2.5) 假设(O1):K=K1+K2,Ki≥0,i=1,2;K1为有界算子,K2为紧算子。 定理3.1[5]假设(O1)被满足,且存在数λ0,使得∀λ>λ0,有 rσ(BλK1) <1. (3.1) (2)若rσ(Bλ0K2) >1,则有σ(A)≠∅。 其中σ(A)表示迁移算子A的谱集。 (3)σ(A)∩{λ∈|Reλ>-σ}仅由有限个具有限代数重数的离散本征值组成。 引理3.2[5]迁移算子A在空间X上产生正不可约C0半群。 引理3.3[8]迁移算子A是空间X上的正不可约C0半群,则A(A*)的正本征函数为严格正的。其中A*为A的共轭算子。 为了给出迁移方程(1.1)解的大时间渐近行为,我们将证明该方程(1.1)相应的迁移算子A的占优本征值的存在性。为此,我们先引入算子的占优本征值的定义: 定义3.4[9]设A是Banach空间X上的闭稠定算子,β0是A的离散本征值,若 (1)β0是一个实数; (2)β0的代数重数为1; (3)∀λ∈σ(A),λ≠β0,Reλ<β0; (4)β0是A的具非负本征函数的唯一本征值。 定义3.5[8]设F∈X,则对G∈X,定义 从文献[8,A-III,3.6],我们引入留数的定义.设λ0∈σ(A) 是A的离散本征值,函数R(λ,A)关于λ的Laurent级数为: 其中系数bn是有界线性算子,且 (3.2) 系数b-1为谱集{λ0}的谱投影,被称为R(·,A) 在λ0的留数,且被表示为 由(3.2)式可知: b-(n+1)=(A-λ0I)n·P,b-(n+1)·b-(m+1)=b-(n+m+1),n,m≥ 0. (3.3) 如果存在k>0,使得b-k≠0,且对一切n>k,有b-n=0,则λ0被称为R(·,A)的k阶极点。根据(3.3)式,有b-k≠0,b-(k+1)=0。由此可知: (3.4) 由于P是正的,则P*(P的共轭)也是正的。根据定义3.5,对φ,φ∈X,有 定理3.6如果假设(O1)成立,则β0是迁移算子A的占优本征值。 证明.(1)根据定理3.1,我们知道β0是实数。 (2)现在,我们需要证明β0的代数重数为1.以下分两步证明。 第一步 找一个函数ψ0∈ker(β0I-A)是严格正的。 事实上,对λ>λ0≥β0,其阶数是k,则由(3.4)式知:k是Laurent级数的最高系数。即 易知:b-k正算子,则存在g≥0,使得ψ0:=b-kg≥0,且 即ψ0是β0的一个正本征函数,根据引理3.3,知道ψ0是严格正函数。 此外,若ker(β0I-A)含一个严格正函数ψ0,则β0是一阶级点。 PD(A)=ker(β0I-A),P*D*(A)=ker(β0I-A*). (3)现在我们来证明定义3.4(3),即∀λ∈σ(A),λ=β0,有Reλ<β0.事实上,我们仅需证明Reλ≠β0,因为β0是谱界。 首先,我们说明:若∀ψ∈ker(β0-A),ψ≠0,则|ψ|∈ker(β0-A). 因为Aψ=β0ψ,则U(t)ψ=eβ0 tψ([8,A-III,Cor.6.4]).由于U(t)是正的,则 eβ0 t|ψ|=|eβ0 tψ|=|U(t)ψ|≤U(t)|ψ|,i.e.U(t)|ψ| -eβ0 t|ψ| ≥ 0, (3.5) (3.6) A|ψ|=β0|ψ|. (3.7) 现在,假设Reλ=β0,令λ=β0+iα,α≠0,根据(3.7)式,有A|ψ|=β0|ψ|,其中ψ∈ker(β0I-A),所以β0+iαn∈σ(A) (n∈N)[8]。这当n充分大时与定理3.1(3)矛盾即∀λ∈σ(A),λ=β0,有Reλ<β0. (4)最后,我们证明定义3.4(4),即β0是A的唯一具有非负本征函数的本征值。 假设有另一本征值λ,其中λ=β0,ψ∈X,ψ≠0是它的本征函数,则 因此,根据定义3.4,我们完成了定理3.6的证明。 [1]RotenbergM.Transporttheoryforgrowingcellpopulations[J].JtheorBiol, 1983, 103: 181-199. [2]BoulanouarM.Transpotequationincellpopulationdynamics(I)[J].ElecDiffEquaN, 2010, 144:1-20. [3]BoulanouarM.Transpotequationincellpopulationdynamics(II)[J].ElecDiffEquaN, 2010, 145:1-20. [4]王胜华,翁去芳,阳名珠.人体细胞增生中的一类迁移算子的谱分析[J].数学物理学报,2010,30A(4):1055-1061. [5]王胜华,吴军建.种群细胞增生中一类Rotenberg模型[J]. 应用泛函分析学报,2014,16(4):296-303. [6]BoulanouarM.Transpotequationforgrowingbacterialpopulations(I)[J].ElecDiffEqua, 2012, 221:1-25. [7]BoulanouarM.Transpotequationforgrowingbacterialpopulations(II)[J].ElecDiffEqua, 2012, 222:1-21. [8]NagelR,GreinerG,LectureNotesinMathematics[M].NewYork:Springer, 1986. [9]WangShenghua,YangMingzhu,XuGenqi,Thespectrumofthetransportoperatorwithgener-alizedboundaryconditions[J].TransportTheoryandStatisticalPhysics, 1996,25(7):811-823. [10]YangMingzhu,ZhuGuangtian.Spectrumofneutrontransportoperatorwithanisotropicscat-teringandfission,Scientia Sinica, 1981,(4):476-482. Dominant Eigenvalue's Problem of a Transport Operators in Bacterial Population WANG Sheng-hua1, PAN Shi-fu2 (1.School of Mathematics & Computer Science, Shangrao Normal University,Shangrao Jiangxi 334001,China; 2.Department of Methmetics of Nanchang University,Nanchang Jiangxi 330031,China) The objective of this paper is to research that the transport equations for a growing bacterial populations model with generalized boundary conditions inL2space.itistoobtainthattheexistenceofdominanteigenvalueforthetransportoperator. bacterial populations; generalized boundary conditions; transport equation; transport operator; dominant eigenvalue 2015-11-28 国家自然科学基金资助项目(11461055);江西省自然科学基金资助课题(2015BAB201029) 王胜华(1956-),男,江西余干,教授,博士,研究方向:迁移方程。E-mail:wshua@sru.jx.cn 0177.2 A 1004-2237(2015)06-0001-05 10.3969/j.issn.1004-2237.2015.06.001
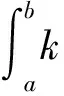
2 准备知识

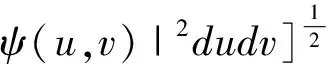


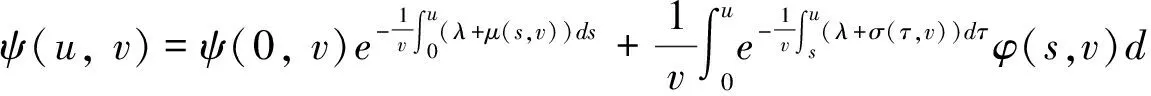
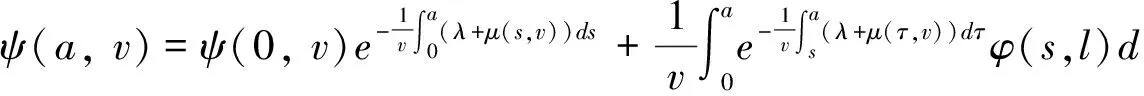
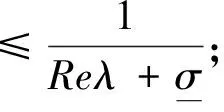
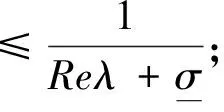
3 算子A的谱