电动汽车动力总成悬置系统优化

李尧尧, 王 晖

(江苏大学 汽车与交通工程学院，江苏 镇江 212013)



电动汽车动力总成悬置系统优化

李尧尧, 王 晖

(江苏大学 汽车与交通工程学院，江苏 镇江 212013)

建立了某电动汽车动力总成悬置系统六自由度数学模型和ADAMS仿真模型，对系统进行了模态分析和振动响应分析,研究了系统的振动特性。选择动力总成悬置支承处动反力最小为优化目标，各个悬置的轴向静刚度为设计变量，动力总成固有频率合理分布以及各个悬置和总成位移等为约束条件，利用 ADAMS/Insight 对悬置参数进行优化。结果表明优化悬置刚度参数后，驾驶员耳旁测点平均声压级有明显的降低，降低了13%，特别是在声压值较高点降低尤其明显，降低了21%，很好地达到了隔振降噪的目的。

车辆工程；电动汽车；动力总成悬置系统；声压级

动力总成悬置是指动力总成与车架之间的弹性连接元件，可以衰减两者间的振动传递，有隔振、支承和限位的作用。动力总成悬置系统的隔振降噪性能只对整车的NVH性能有很大影响[1-3]。当前，国内外学者在动力总成悬置系统优化设计匹配方面做了大量的研究。常见的研究方法有能量解耦和转矩轴解耦。徐中明[4]，徐石安[5]，温任林，等[6]在这些方面做了深入研究，研究了悬置系统参数对悬置系统的解耦鲁棒性、固有频率的影响。然而对纯电动汽车动力总成悬置系统的研究比较少。

针对传统的内燃机汽车，对其动力总成优化的方法有许多，有正交优化设计方法进行变量优化；合理布置悬置点安装位置和安装角度以获得较好隔振效果的方法；综合考虑各子系统的模态影响,以车内噪声为目标进行优化等等。电动机与发动机的特性是不同的，借鉴传统的分析方法，在研究纯电动汽车动力总成悬置系统隔振问题时，电动机的特点是必须要考虑的。

笔者考虑到电动机与发动机的差异性建立了某电动汽车动力总成悬置系统六自由度数学模型和ADAMS仿真模型，对系统进行了模态分析和振动响应分析，以动力总成悬置支承处动反力最小为优化目标，探索一种有效途径来解决电动汽车动力总成悬置系统的振动问题。

1 系统建模

考虑到动力总成悬置系统的固有频率远低于动力总成的固有频率，并且根据具体的动力总成悬置系统和悬置数目，可将动力总成作为刚体考虑。由此动力总成悬置系统的简化模型为：通过3个三维的黏-弹性悬置元件支承在车架上，具有6个自由度。图1为动力总成三点式悬置位置布置。

图1 电机动力总成悬置系统悬置位置与编号

图1中，①②③分别表示各个弹性悬置元件的位置。动力总成悬置系统的坐标系原点O选在电机风扇罩端面中心处，X轴与水平面平行，指向为汽车行驶方向，Z轴方向是垂直向上，Y轴与电机转子轴线平行，依据右手定则确定方向。X，Y，Z轴上的平动x，y，z和绕X，Y，Z的转动α，β，γ为动力总成的振动，动力总成广义坐标表示为:

(1)

根据振动理论，建立动力总成悬置系统六自由度振动的运动微分方程式如式(2)：

(2)

将式(2)拉氏变换转换到频域内，不考虑阻尼和外力作用可得式(3)：

(3)

式中：ω为固有频率。

2 系统模态和振动响应分析

2.1 模态分析

固有频率作为悬置系统的重要特性，分析系统的固有频率来判断其是否满足隔振要求。通过式(3)可得出固有频率。通过ADAMS/Vibration 模块来计算系统的各阶固有频率和能量分布百分比，如表1和表2。

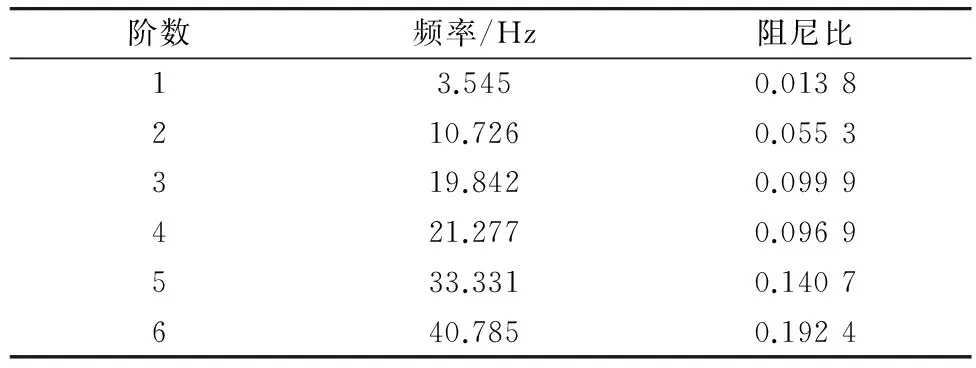
表1 系统固有频率

表2 动力总成悬置系统能量分布百分比

从表1可以看出，1阶固有频率过低，容易在路面的激励下产生共振，第6阶固有频率过高，容易与电机工作频率重合，产生共振。阻尼比很小，因此在以后的优化过程中不必考虑悬置阻尼对系统的影响。从表2可以看出，动力总成悬置系统解耦性能不太理想，Y向与Rzz向振动存在一定程度的耦合。耦合程度最为严重的是第4阶Rzz向，其能量最多，为31.65%；但是Z向振动模态能量占到25.46%，Ryy向占18.12%；Rxx向占14.86%。在这个模态下，能量分布非常散，Rzz向振动与其它几个自由度的耦合程度非常高。因此在合理布置固有频率的同时需保证各自由度能量解耦[7]。

2.2 系统时域仿真分析

将动力总成三向激励加载于动力总成悬置系统ADAMS模型的相应位置点，并对其进行仿真。图2为橡胶悬置1分别在u，v，w向动反力响应。橡胶悬置1在u，v，w向位移响应见表3。

图2 悬置1 在u，v，w向动反力响应

悬置1的3个方向uvw位移均方根值/m0.00080.00030.0018

通过对图2和表3分析，可以得到悬置1的以下动态特性：

1)在振动初始时，振动幅值较大且较复杂，这是由于初始振动时，系统自由振动与强迫振动相互叠加，经过一段时间，自由振动的振幅很小，忽略不计，最后主要是激励力引起的强迫振动。

2)悬置u，w向受剪切应力，v向受拉压应力，u，w向受力明显高于v向，这是因为u，w向均直接作用有激励并且还会受到绕Y轴转矩激励My的影响；而v向只存在由惯性力产生的瞬时激励Fy，此惯性力在直线匀速行驶时很小，可忽略不计，v向的受力主要是由于悬置系统的自由度耦合引起的激励。

3)悬置u，v，w向均产生了不同程度的变形，其中w向变形最大，达0.001 8 m，但变形量都在合理的范围内。

对悬置2和悬置3动态特性进行仿真分析，可得到与悬置1相同的结论。

2.3 系统频率仿真分析

对系统ADAMS模型进行仿真得到悬置支承处响应力频谱特性，如图3。

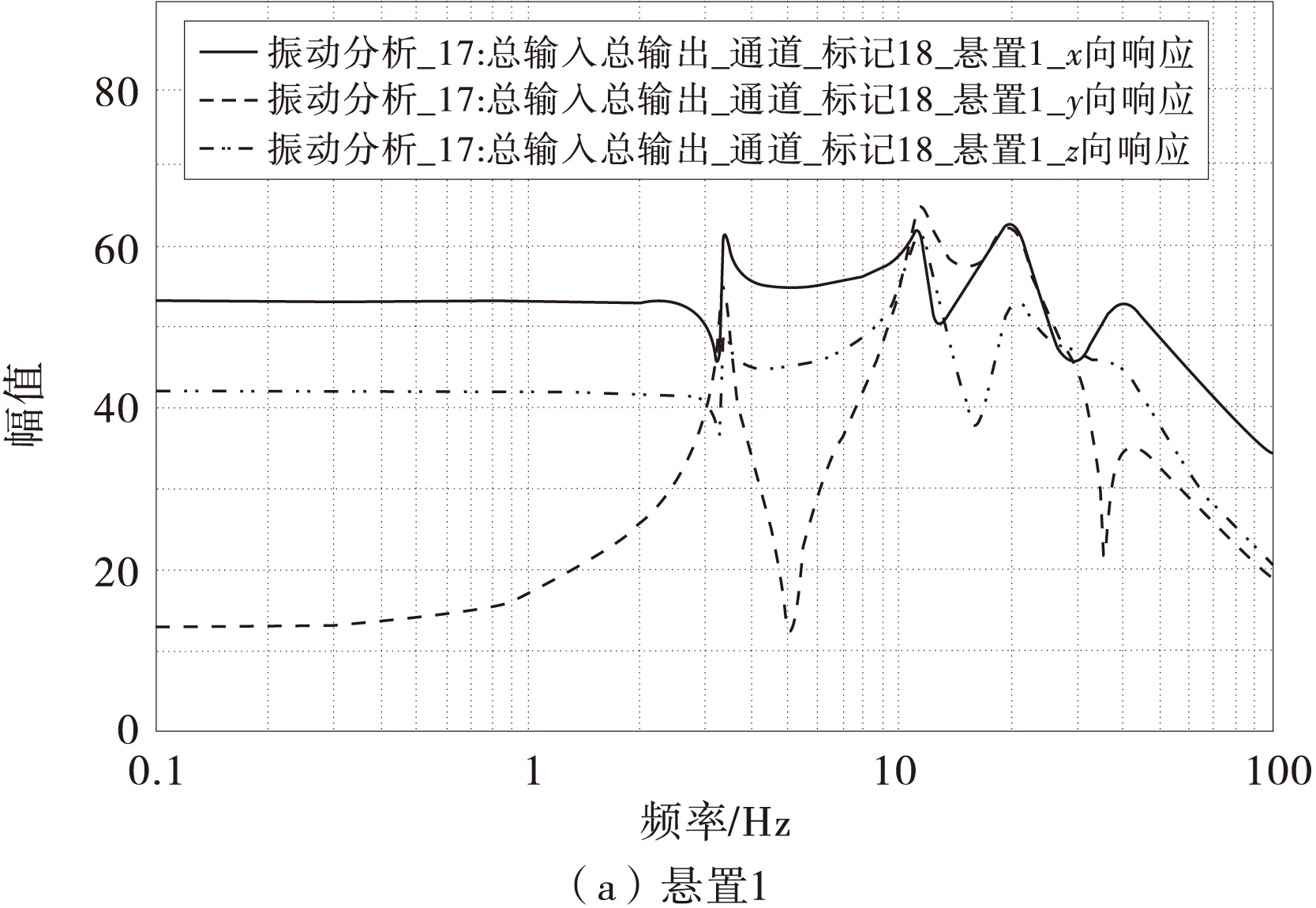
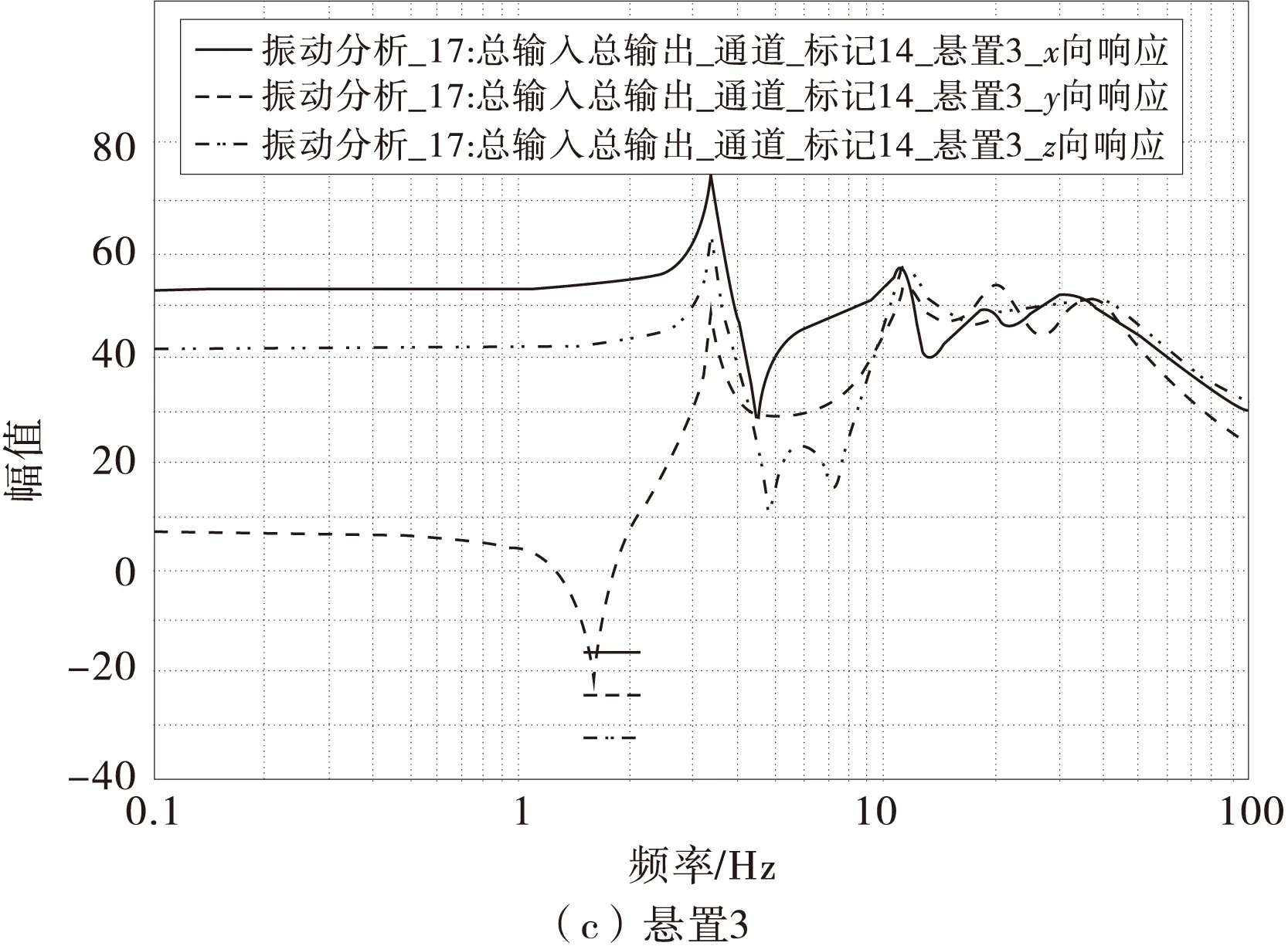
图3 悬置1，2，3动反力频谱响应

从图3可看出开始响应曲线是线性的，之后进入系统的6个固有频率，从而引发了共振，最大共振出现在3.5 Hz处，这是由于动力总成悬置系统第1阶模态受激发引起的。随后进入电机的工作频率，在50 Hz之后随着频率的增加，悬置支承处动反力力幅值都出现了不同程度的减小。通过隔振原理可知，激励频率和固有频率的比值越大，系统的隔振性能也就越好。因此需合理布置动力总成悬置系统固有频率，防止共振的发生。

3 悬置系统优化

3.1 优化目标

优化设计动力总成悬置参数时，可从多个角度提出多个目标函数。通常动力总成悬置系统的目标函数有：系统各自由度解耦率、系统固有频率的合理匹配、悬置支承处动反力最小和垂直方向的振动加速度均方根值最小等。由前面分析可知，动力总成振动通过悬置传递到车身的激励力是引起车身板件振动从而辐射噪声的主要原因。因此从降低车内噪声出发，设计目标函数取为悬置支承处动反力振幅最小，响应力振幅越小，说明其综合隔振效果越好。样车动力总成支承方式为三点式，因此共3个优化目标，分别记悬置1、悬置2、悬置3支承处动反力优化目标为object1，object2，object3[8]。

3.2 设计变量

设计变量就是优化过程中要确立的变量。系统的动力学特性和悬置元件的阻尼、刚度、安装位置等因素有关。实际过程中，对已成型的动力总成悬置系统进行优化设计时，系统自身的特性参数如质心、质量和转动惯量等是不会变的，所以只能对悬置元件物理、几何特性参数进行优化，主要是系统阻尼、刚度及悬置元件的安装位置、角度等。样车受到电机动力总成安装空间位置的限制，考虑经济性，悬置元件仍采用原来的布置形式，即悬置元件的安装位置和角度不变。另外，在微小振幅振动下，系统的动态特性受橡胶悬置阻尼的影响很小，因此设计变量的选择主要针对每个悬置元件的三向静刚度，共9个设计变量，见表4。

表4 设计变量编号

3.3 约束条件

在优化设计过程中，约束条件是对设计变量取值时的限制条件。由于约束条件的存在，使得为求解满足设计约束条件的设计点的工作难度加重，但其优化结果更符合实际的要求，能达到最佳的优化效果。动力总成悬置系统优化设计的约束条件可概括为：

2)确保动力总成在工作时振动不能过大从而影响连接管路、周围零部件和仪表正常工作。如果垂向位移和侧向位移太大，会缩短悬置元件的寿命。规定电机动力总成质心位移不得超过11 mm，悬置的侧向位移不得超过1 mm，垂向位移不得超过4 mm。

3)根据刚度变化的合理性，将橡胶悬置刚度变化范围设置在±100%之间。

3.4 优化结果分析

SQP(Sequential Quadratic Programming)算法常优于拉格朗日乘子法，是求解非线性约束优化问题的一类最有效的算法。动力总成悬置系统优化问题是一个非线性优化问题。因此采用SQP算法求解。优化后的悬置静刚度见表5。通过对比原悬置静刚度表1可知，改进后的悬置1的u向和悬置3的w向刚度有明显增加，悬置2的u向刚度有明显减小，其余方向刚度值变化不大。

表5 优化后的悬置静刚度

优化后的电机动力总成悬置系统固有频率分布见表6。通过对比原动力总成悬置系统固有频率分布表2可知，系统优化后的固有频率在4.935～23.699 Hz之间，最高阶固有频率比优化前有一定降低，避开了电机的工作频率，最低阶固有频率比优化前有一定的提高，避免了路面激励引起的共振。而且各阶固有频率之间间隔在2 Hz以上，频率分布更加合理。

表6 优化后的电机动力总成悬置系统固有频率

优化后电机动力总成悬置系统能量分布百分比见表7。通过对比表3分析可知，在能量分布上，解耦程度均有提高，其中最明显的是第4阶从31.65%提高到80.22%，其余阶数解耦度均在60%以上，基本上达到了各自由度解耦，优化效果比较理想。

表7 优化后电机动力总成悬置系统能量分布百分比

选取计算频率为0～100 Hz，频率增量的步长为2 Hz，计算得到驾驶员耳旁测点声压级并与优化前作比较，如图4。从图4可以看出，在各频率处声压值都有所降低，通过计算驾驶员耳旁测点平均声压级降低了13%，特别是在45，65，95Hz处声压值降低较明显，降低达到了21%。在60，72 Hz处声压值略微有所增大，但是增大的幅度并不大，而且此频率处声压值本来就不高，所以并不影响整体车内噪声的降噪效果。优化结果表明此优化方法有效可行，可以起到隔振降噪的效果。

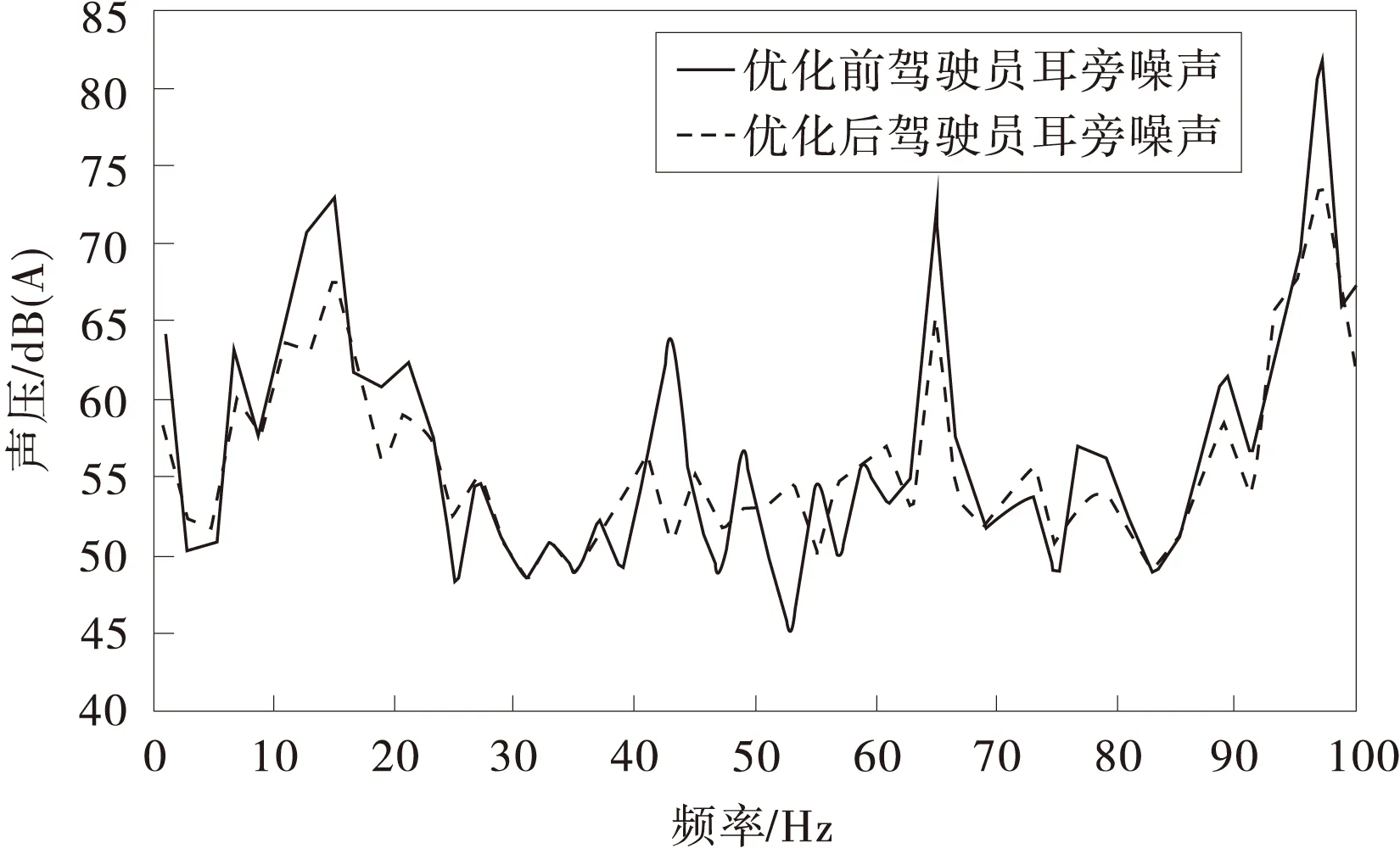
图4 优化前后驾驶员耳旁噪声声压值对比

4 结 语

建立了样车电机动力总成悬置系统的六自由度仿真模型，分析了其固有模态与固有振型以及振动能量耦合情况。从模态频率和能量分布百分比可以得出电机动力总成悬置系统存在多自由度耦合现象。并且通过悬置系统在常用工况下的动态响应分析，指出悬置系统隔振效果不理想。选择以悬置支承动反力最小为优化目标，以悬置静刚度为设计变量，以电机动力总成悬置系统固有频率合理配置、悬置变形、系统位移为约束条件，采用SQP算法优化悬置系统参数，分析和评价了优化结果，结果表明优化悬置刚度参数后，驾驶员耳旁测点平均声压级有明显的降低，降低达到13%，特别是在45，65，95 Hz处声压值较高点降低尤其明显，降低达到了21%，很好地达到了隔振减噪的目的。

[1] 王珣,张立军.燃料电池轿车电动动力总成悬置系统动态特性分析[J].汽车技术,2009(2):28-35. Wang Xun,Zhang Lijun.Study on dynamic characteristic of electrical powertrain mounting system for a fuel cell vehicle [J].Automotive Technology,2009(2):28-35.

[2] H Hata,H Tanaka.Experimental Method to Derve Optimum Engine Mount System for Idle Shake [R].U.S.A:SAE Paper,1987.

[3] 梁天也,史文库,唐明祥.发动机悬置研究综述[J].噪声与振动控制,2007(1):6-10. Liang Tianye,Shi Wenku,Tang Mingxiang.The summary of study in engine mounting [J].Noise and Vibration Control,2007(1):6-10.

[4] 徐中明.纯电动汽车动力总成悬置系统的优化[J].汽车工程,2012,34(9):807-810. Xu Zhongming.Optimization of the powertrain mounting system of electric vehicle [J].Automotive Engineering,2012,34(9):807-810.

[5] 徐石安.汽车发动机弹性支承隔振的解耦方法[J].汽车工程,1995,17(4):198-204. Xu Shian.Vibration isolation and decoupling technique of engine-mount on vehicles [J].Automotive Engineering,1995,17(4):198-204.

[6] 温任林,颜景平.汽车发动机悬置系统多目标的研究[J].东南大学学报,1996,26(6A):106-112. Wen Renlin,Yan Jingping.Study on multi-objective optimization of engine mounting system [J].Journal of Southeast University,1996,26(6A):106-112.

[7] 王天利,孙营.基于能量法解耦的汽车动力总成悬置系统优化[J].机械设计与制造,2006(7):31-33. Wang Tianli,Sun Ying.The optimization of vehicle powertrain mounts system based on energy decoupling [J].Machinery Design & Manufacture,2006(7):31-33.

[8] 薛念文,高非.电动汽车动力传动系统参数的匹配设计[J].重庆交通大学学报:自然科学版,2011,30(2):304-307. Xue Nianwen,Gao Fei.Matching of parameters of power transmission for electric vehicles [J].Journal of Chongqing Jiaotong University:Natural Science,2011,30(2):304-307.

Optimization of the Power Train Mount System of Electric Vehicle

Li Yaoyao, Wang Hui

(School of Automobile & Traffic Engineering, Jiangsu University, Zhenjiang 212013, Jiangsu, China)

The power train mount system of electric vehicle with six degrees of freedom mathematical model and ADAMS simulation model were established. By analyzing the mode and vibration response of the mount system, the characteristics of mount system vibration was researched. Firstly, that the dynamic reaction force at the supporting of power train mount reached the minimum value was chosen as the optimal objective; secondly, the axial static stiffness of each mount was chosen as design variables; thirdly, the reasonable distribution of power train inherent frequency, mount and power train displacement were chosen as constraint conditions; finally, the optimization on mount parameters were conducted with ADAMS/Insight. The results show that the driver’s average sound pressure level at ear point is significantly reduced by 13%, and it was even reduced by 21% on the higher sound pressure level. The optimization well achieves the purpose of the noise reduction of vibration isolation.

vehicle engineering; electric vehicle; power train mount system; sound pressure level

10.3969/j.issn.1674-0696.2015.01.29

2013-03-13；

2013-05-31

李尧尧(1987—)，男，江苏宿迁人，硕士研究生，主要从事电动汽车动力总成悬置系统方面的研究。E-mail：550748909@qq.com。

U469.72

A

1674-0696(2015)01-135-05