基于投资者情绪的市场均衡分析

谢 军 , 高 斌

(1.广西大学 数学与信息科学学院，广西 南宁 530004； 2.华南理工大学 经济与贸易学院，广东 广州 510006)



基于投资者情绪的市场均衡分析

谢 军1, 高 斌2

(1.广西大学 数学与信息科学学院，广西 南宁 530004； 2.华南理工大学 经济与贸易学院，广东 广州 510006)

在行为金融研究框架下，通过分析情绪投资者与理性投资者的市场均衡条件，构建基于投资者情绪的资产定价模型，并对模型进行了数值模拟。结果表明，投资者情绪是影响资产价格的重要因素：被情绪投资者高估的资产，其回报将下降；被情绪投资者低估的资产，其回报将增加；资产回报的变化程度与情绪投资者卖出低估资产的份额正相关，与资产预期回报金额的相关系数负相关；并且，乐观情绪与悲观情绪对资产价格的作用是非对称的。

行为金融；投资者情绪；市场均衡；资产价格

0 引言

标准金融资产定价理论建立在有效市场假设(EMH)之上，以理性人为假设基础，认为市场只有理性的投资者，且具有同质信念，都清楚的知道资产回报的真实联合分布。然而，Kahneman和Tversky[1]通过实验对比发现，大多数投资者并非是标准金融投资者，投资者的行为并不总是理性的。Black[2]也认为投资者购买资产的依据并不是资产的基础价值信息。并且，现实金融市场中的长期反转现象[3,4]、封闭式基金折价之谜[5]、动量效应[6]等大量金融异象的出现，也都表明理性人假设的有着很大的局限性。现实金融市场的定价分析过程，除了受基础价值、传统风险的因素影响外，还应考虑投资者心理、行为等多方面因素。

为此，在均衡资产定价领域，DeLong等[7]建立的DSSW模型打破了市场只有理性投资者的假设。Daniel等[8]在考虑投资者过度自信和有偏的自我归因, 建立了可用以解释股票收益短期动量和长期反转的DHS模型。Barberis等[9]通过分析保守主义和代表性偏差构建了BSV模型。Hong和Stein[10]研究了由消息观察者和动量交易者两种类型的有限理性投资者作用下的市场均衡定价问题。近来，Fama和French[11]考虑了投资者偏好对资产价格的影响；然而，正如杨春鹏[12]总结的，现今已有归纳的投资者心理、行为偏差就有三十多种，当前依据投资者行为、心理偏差的资产定价研究往往只利用一、两种心理偏差来针对性构建模型，这就造成了行为金融研究存在分散、无逻辑和内涵模糊等内在局限性[13]。

史金艳等[14]研究了基于投资者异质信念的均衡资产定价问题，试图突破以往行为均衡定价模型中依据片面心理、行为偏差假设的局限性。与之不同，鉴于当前大量实证[15～18]研究表明投资者情绪是影响资产价格的重要因素。本文试图以投资者情绪来取代投资者行为、心理偏差(从而避开了对众多心理偏差的探讨)，探讨在情绪投资者作用下、市场均衡情况下的资产定价问题。本文从理论建模和数值模拟两方面对这一问题进行探讨。(1)通过分析情绪投资者、理性投资者在均衡定价中的作用，建立一个基于投资者情绪的均衡资产定价模型，阐释了情绪投资者与资产价格的关系。(2)进一步对本文基于投资者情绪的均衡资产定价模型进行数值模拟，并与理性资产定价进行对比，更深入、具体地探讨投资者情绪对资产价格的影响。

1 基于投资者情绪的市场均衡模型

当市场是有效的，投资者表现为理性投资者时，CAPM的切点组合T就是市场组合M，即T=M。然而投资者受情绪影响的情况却是常见的，池丽旭, 庄新田[16]给出了中国证券市场投资者情绪与股票收益关系的实证检验结果；Chiang等[17]检验了投资者情绪与资产泡沫间的关系；Hwang[18]提供了情绪导致资产价格偏离基础价值的证据；Fisher和Statman[19]以及Brown和 Cliff[20]也实证表明投资者情绪是影响资产价格的重要因素。本文以此为契机，在市场没有资金流入、流出的前提下，考虑市场的均衡价格，建立模型说明情绪投资者对资产价格的作用。

(1)模型假设。考虑市场由情绪投资者S及理性投资者T构成，情绪投资者受到错误信息的影响，产生乐观情绪时高估资产价值、产生悲观情绪时低估资产价值；而理性投资者对市场进行纯理性的分析，即按CAPM模型进行投资，拥有切点组合上的风险资产组合。

为简单起见，假设开始时理性投资者T拥有资产H与资产L各1单位。而由于情绪投资者S对资产H悲观低估，从而卖出份资产H给理性投资者，即此时理性投资者T共拥有1+θH份资产H；情绪投资者S对资产L乐观高估，从理性投资者手中买入份资产L，即理性投资者此时还拥有1-θH份资产L；市场期望回报E(RM)、无风险利率Rf及夏普率ST为常数。

(2)模型构建。为求出每单位资产H的市场均衡价格VH及每单位L的市场均衡价格VL，假设每单位资产H回报的总金额为PH，每单位资产L回报的总金额为PL。所以资产H的收益RH及资产L的收益RL为：E(RH)=E(RH)/VH，E(RL)=E(PL)/VL。 记φΗ1+θH，θL1-θL，由市场均衡

(θH-1)VH-(1-θL)VL=0

(1)

RT=(θLPL+φHPH)/(φLVL+φHVH)

(2)

其中RT为理性投资者拥有的切点组合T的收益。则

(3)

记PH的波动率为σH，PL的波动率为σL，PH与PL间的相关系数为ρ，代入上式计算得

(4)

类似的，

(5)

公式(4)、(5)描述了悲观情绪引起的低估资产H与乐观情绪引起的高估资产L的市场均衡价格与如下变量有关：无风险利率Rf，切点组合夏普率ST；对资产H、L的预期回报总金额E(PH)、E(PL)，及相应的波动率σH、σL；资产H与L的相关系数ρ及卖出低估资产H的份额θH与买入高估资产L的份额θL。

进一步的，讨论组合H，L的回报，不妨假设E(PH)=αE(PL)，σH=βσL，显然如果相关系数ρ=1，即乐观情绪引起的高估资产L与悲观情绪引起的低估资产H完全正相关，必然会导致θH或θL为零，所以此时没有发生市场买卖，即市场仍将是CAPM均衡，因此组合H、L及切点组合T的回报都应该等于理性的CAPM定价所确定的价格。

下面考虑悲观低估资产H与乐观高估资产L的相关系数小于1的情形，由(4)、(5)得：

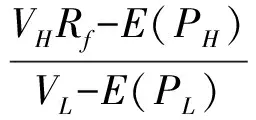
(6)

(6)式左边分子、分母同时除以VH，并把(5)式代入，解得

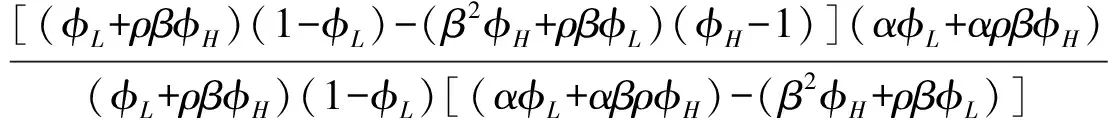
(7)

(6)式左边分子、分母同时除以VL，并把(5)式代入，解得

(8)

也就是说情绪投资者悲观低估的资产H与情绪投资者乐观高估的资产L的期望与无风险利率Rf、低估资产L与高估资产H的相关系数ρ、比例系数α、β及买卖数量φH、φL有关。

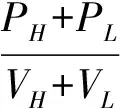
(9)

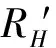
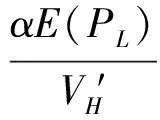
(10)

类似的，对资产L有：

(11)

由(10)、(11)解得

记

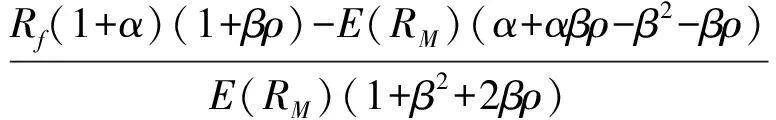
(12)

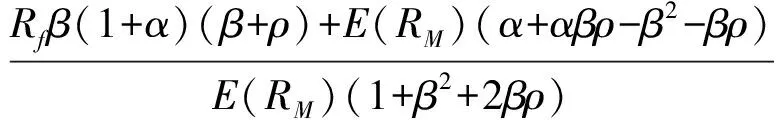
(13)

则

(14)

(15)

把(14)、(15)带入到(9)得：

(16)

当情绪投资者对资产H、L低估、高估产生交易时，注意到σH=βσL，则由(5)式知：

(17)

(16)、(17)分子分母同时除以VL，联立得

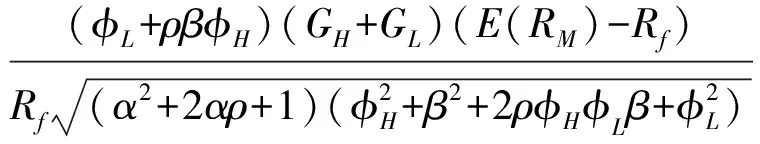
(18)

最后联立(7)、(8)、(12)、(13)、(18)式，即可求出期望收益与相关系数ρ及φH之间的关系。从而确定资产在投资者情绪影响下的均衡价格。

2 数值模拟

本节用Matlab软件对上节构建的基于投资者情绪的市场均衡模型进行编程模拟，具体参数赋值见表1。对数值模型参数的进一步说明：α=0.9，β=1，表明情绪投资者对资产H低估的总回报金额为资产L的0.9倍，而资产H与资产L的回报金额有相同的波动，即E(PH)=0.9E(PL)，σH=σL。

表1 数值模拟参数说明

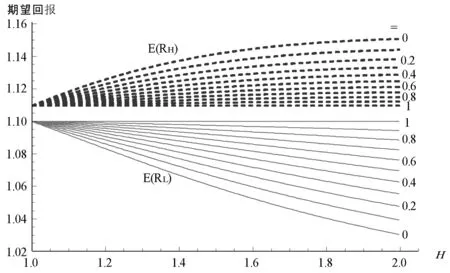
数值模拟结果图1显示，情绪投资者对市场造成重大影响：低估资产H与高估资产L的回报会随着情绪投资者卖出、买入的份额产生较大的变化。例如，取定ρ=0.2，当情绪投资者卖出低估资产H的份额从0.2增大到0.8时(即φH从1.2变化到1.8)，此时对低估资产的期望回报E(RH)将从1.12增大到1.14；对应的，对高估资产的期望回报E(RL)将从1.09减少到1.06。从图1中知道低估资产H与高估资产L的回报受到H，L的期望回报金额间的相关系数ρ的影响。例如，取定φH=1.6，当相关系数从0.2变化到0.8时，低估资产H的期望回报将从1.13下降到1.11，而高估资产的回报将从1.07上升到1.09。Longin和Solnik[21]以及Cheung和Miu[22]的研究表明证券市场资产的相关系数是动态变化的，熊市和牛市的相关系数存在显著差异，一般的熊市相关系数大于牛市相关系数。可见，熊市资产间的相关系数大，将导致资产间回报差异小。因此，熊市中的投资者在处置资产时，抛售任何资产都是正确的投资策略。而牛市资产间的相关系数小，将导致资产间回报差异大。因此，牛市中的投资者在处置资产时，买入资产的选择将有重要意义：买入正确的资产才能获得高额回报。这就解释了为什么出现投资者在牛市中也赚不到钱的现象。

最后，我们考察系数α、β对低估资产H、高估资产L期望回报的影响。图4分析系数α对资产期望回报的影响。取β=1 ，φH=1.6，ρ=0.8,其它参数如图1所取，当α∈(0.1,1)，即当对资产H低估与对资产L高估的系数逐步变大，即低估、高估的程度逐步缩小时，显然其低估资产与高估资产的回报差距逐渐缩小。但是从图4，我们注意到资产H低估与对资产L高估的系数，对高估资产L的影响明显比对低估资产H的影响小。例如，当β从0.2变化到0.8时，低估资产H的期望回报E(RH)将从1.6变化到1.13，高估资产L的期望回报E(RL)将仅从1.095变化到1.094。

图5分析系数β对期望回报的影响。取α=1，φH=1.6，ρ=0.8，其它参数仍如表1所取，当β∈(1,10)，当对资产H的预期回报总金额的波动率与对资产L预期回报总金额的波动率间的系数逐步变大，即低估、高估的程度逐步扩大时，显然其低估资产与高估资产的回报差距逐渐扩大。但是从图5，我们注意到资产H低估与对资产L高估的系数对高估资产L的影响明显比对低估资产H的影响小。例如，当β从2变化到8时，低估资产H的期望回报E(RH)将从1.2变化到2.6，高估资产L的期望回报E(RL)将仅从1.091变化到1.088。

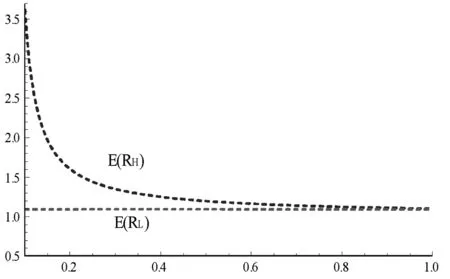
图4 α对期望回报的影响

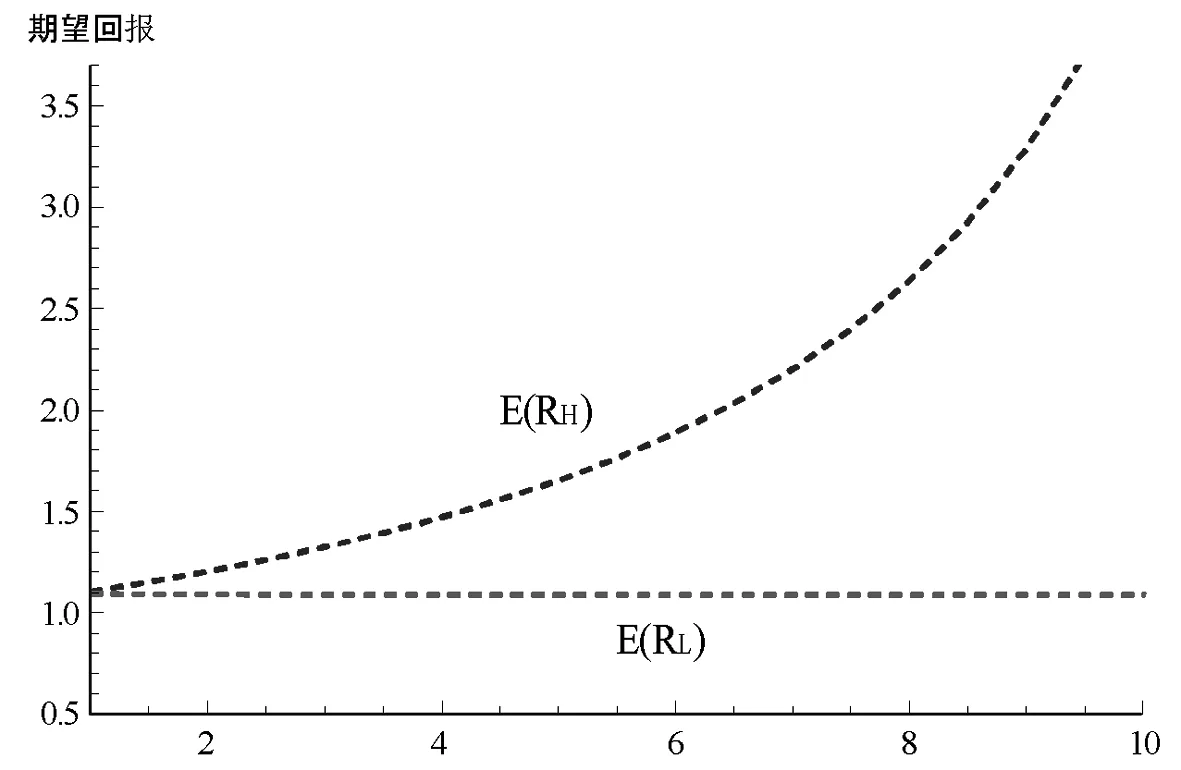
图5 β对期望回报的影响

总之，当仅考虑系数α、β对系统的影响时，如果把期望回报的预期作为投资者参与市场买卖资产(股票)的动力，则投资者情绪或许正是现实金融市场上股票价格上涨的速度慢于下跌的速度的模型解释：当市场乐观时，投资者普遍对大量资产(股票)高估，但是由图4、图5的分析我们知道，系统参数α、β的变动并不能引起对已经高估的资产(股票)的期望收益产生太大的变化，考虑到交易费用等问题就造成了投资者缺乏参与市场的动力(由于投资者是乐观的，投资者更偏向于买入资产，但是预期到大部分的高估资产的期望回报变动不大，投资者仍会处于观望状态，拒绝买入。从而造成资产(股票)价格上涨的速度不快；而当市场悲观时，投资者普遍对大量资产(股票)低估，但是由图4、图5的分析我们知道，系统参数α、β的变动并将引起对已经低估的资产(股票)的期望收益产生剧烈的变化，这就导致投资者有强烈参与市场的欲望(由于投资者是悲观的，投资者将更倾向于卖出资产)，从而造成资产(股票)价格下跌的速度非常快。

3 结论

本文探讨理性投资者和情绪投资者共同参与的市场的情况下，通过市场出清，构建了情绪投资者在其中起重要作用的均衡定价模型，并且进一步通过数值模拟探讨了投资者情绪对资产回报的影响。情绪投资者对资产L乐观高估，对资产H悲观低估，将导致资产L的回报下降、资产H的回报增加。且资产L的回报下降及资产H的回报增加的程度都与情绪投资者卖出低估资产的份额θH(θH=φH-1)正相关，而与资产L、H的预期回报总金额的相关系数ρ负相关。整体而言，熊市相关系数大于牛市相关系数。因此，熊市中的投资者在处置资产时，抛售任何资产都是正确的投资策略。而牛市资产间的相关系数小，资产间回报差异大。因此，牛市中的投资者在处置资产时，买入正确的资产才能获得高额回报。这就解释了为什么出现投资者在牛市中也赚不到钱的现象。

通过数值模拟仿真作图，本文发现投资者情绪可以使得资产的回报相对理性时候的回报产生较大的偏差，表明当资产受到除了资产的基本价值外的其它一些因素(如投资者情绪)影响时，资产价格将与标准金融的理性定价理论有很大不同。另外我们指出，乐观、悲观情绪对资产的作用并不是完全对称的，这也就说明市场在牛、熊市的不同阶段，其市场表现可能差别很大。最后，用α、β表示投资者情绪引起对资产高估、低估的程度系数，研究表明该程度系数对低估资产H的影响明显比对高估资产L的影响大。这对现实市场中股票价格上涨缓慢而下跌迅速的现象给出了有效解释。

[1] Kahneman D, Tversky A. Prospect theory: an analysis of decision making under risk[J]. Econometrica, 1979, 47(2): 263-291.

[2] Black F. Noise[J]. The Journal of Finance, XLL(3), 1986. 529-543.

[3] DeBondt W F M, Thaler R H. Does the stock market overreact?[J]. Journal of Finance, 1985, 40, 793- 805.

[4] DeBondt W F M, Thaler R H. Further evidence on investor overreaction and stock market seasonality[J]. Journal of Finance, 1987, 42, 557-581.

[5] Lee C, Shleifer A, Thaler R H. Investor sentiment and the closed-end fund puzzle[J]. Journal of Finance, 1991, 46(1): 75-109.

[6] Jegadeesh N, Titman S. Profitability of momentum strategies: an evaluation of alternative explanations[J]. The Journal of Finance, 2001, 56, 699-720.

[7] DeLong J B, Shleifer A, Summers L H, Waldmann R J. Noise trader risk in financial markets[J]. Journal of Political Economy, 1990, 98, 703-738.

[8] Daniel K, Hirshleifer D, Subrahmanyam A. Investor psychology and security market under-and over-reactions[J]. Journal of Finance, 1998, 53(1): 1839-1886.

[9] Barberis N, Shleifer A, Vishny R. A model of investor sentiment[J]. Journal of Financial Economics, 1998, 49(3): 307-343.

[10] Hong H, Stein J C. A unified theory of underreaction, momentum trading and overreaction in asset markets[J]. Journal of Finance, 1999, 54(6): 2143-2184.

[11] Fama E F, French K R. Disagreement, tastes, and asset prices[J]. Journal of Financial Economics, 2007, 83: 667- 689.

[12] 杨春鹏.非理性金融[M]. 科学出版社, 2008.

[13] 宋军,吴冲锋.金融资产定价异常现象研究综述及其对新资产定价理论的启示[J].经济学(季刊),2008,7(2):701-730.

[14] 史金艳,赵江山,张茂军.基于投资者异质信念的均衡资产定价模型研究[J].管理科学,2009,22(6):95-100.

[15] Kumar A, Lee C. Retail investor sentiment and return comovements[J]. The Journal of Finance, 2006, 61(5): 2451-2486.

[16] 池丽旭,庄新田.中国证券市场的投资者情绪研究[J].管理科学,2008,23(3):79- 87.

[17] Chiang M C, Tsai I C, Lee C F. Fundamental indicators, bubbles in stock returns and investor sentiment[J]. The Quarterly Review of Economics and Finance, 2011, 51: 82- 87.

[18] Hwang B H. Country-specific sentiment and security prices[J]. Journal of Financial Economics, 2011, 100(2): 382- 401.

[19] Fisher K L, Statman M. Consumer confidence and stock returns[J]. Journal of Portfolio Management, 2003, 30: 115-128.

[20] Brown G W, Cliff M T. Investor sentiment and asset valuation[J]. Journal of Business, 2005, 78(2): 405- 440.

[21] Longin F, Solnik B. Extreme correlation and international equity markets[J]. Journal of Finance, 2001, 56(2): 649- 676.

[22] Cheung S, Miu P. Diversification benefits of commodity futures[J]. Journal of International Financial Markets, Institutions and Money, 2010, 20(5): 451- 474.

Market Equilibrium Analysis Based on Investor Sentiment

XIE Jun1, GAO Bin2

(1.CollegeofMathematicsandInformationSciences,GuangxiUniversity,Nanning530004,China; 2.SchoolofEconomicsandCommerce,SouthChinaUniversityofTechnology,Guangzhou, 510006,China)

Under the analysis framework of behavioral finance, emotional investor and rational investor are taken into account. This paper presents the asset pricing model of market equilibrium based on investor sentiment, and gives a numerical simulation. The results show that investor sentiment is the key factor which affects the asset pricing. The asset which is overestimated by emotional investor has the low return, and the asset which is underestimated by emotional investor has the hight return. The increasing level or the decreasing level of return has the positive correlation with the proportion of the asset which is underestimated and sold by emotional investor, and has the negetive correlation with the expected money payoff. Finanly, the asymmetrical effect of optimism and pessimism is showed by our model. We give an effective explanation of why some people may earn nothing in the bull market, and we also give an effective explanation of why the stock price falls rapidly but rises slowly.

behavioral finance; investor sentiment; market equilibrium; asset price

2012- 07-23

国家自然科学基金资助项目(71201037);广西自然科学基金项目(2015jjBA10015)

谢军(1980-)，男，博士，副教授，主要研究领域：金融工程、行为金融；高斌(1984-)，男，博士后，主要研究领域：行为金融。

F830.91

A

1007-3221(2015)06- 0211- 06

10.12005/orms.2015.0215