基于产品生命周期的闭环供应链定价和协调策略研究
卢荣花, 李 南
(1.南京航空航天大学 经济与管理学院,江苏 南京 211106; 2.南京航空航天大学 金城学院管理系,江苏 南京 211156)
基于产品生命周期的闭环供应链定价和协调策略研究
卢荣花1,2, 李 南1
(1.南京航空航天大学 经济与管理学院,江苏 南京 211106; 2.南京航空航天大学 金城学院管理系,江苏 南京 211156)
研究产品生命周期条件下一个制造商、一个零售商组成的闭环供应链的定价和协调策略:制造商第一周期只生产新品,从第二周期开始生产再制造品,并负责回收。建立了两周期、多周期和无限周期下的分散决策模型和多周期下的集中决策模型,得到最优定价和生产策略。结果表明:两周期中,制造商和零售商应根据不同的成本节约额制定不同的批发价、零售价和生产量。多周期中,当成本节约额比较小时,除第一和最后一个周期外,制造商和零售商应采取相同的定价和生产策略;当成本节约额比较大时,除第一和最后两个周期外,制造商和零售商应采取相同的定价和生产策略。无限周期中,除第一周期以外,制造商和零售商都应该采取相同的定价和生产策略。在有限周期情况下,制造商和零售商应通过在前期制定比较低的批发价和零售价,以提高生产量和销售量,使得后期的回收量增大,达到降低成本的目的。通过引入收益共享契约制定合适的批发价和销售收入及再制造收益共享比率可以协调整个闭环供应链。算例验证了上述结论。
闭环供应链;产品生命周期;定价策略;契约协调
0 引言
由于人们环保意识的增强和政策法规的出台,闭环供应链在近十几年的时间里受到了企业界和学术界的重视,而经济利益的驱动也是供应链企业参与闭环供应链的另外一个非常重要的因素,因为和制造成本相比,回收品的再制造成本要低得多[1~3]。很多学者从产品生命周期角度对闭环供应链的定价和协调进行研究。其中,有部分学者对两周期闭环供应链进行研究[4~11]。Ferguson等、徐峰等都是基于异质性消费群体进行定价研究[4,5]。Webster等考虑了回收法规的影响[6]。Atasu[7]等综合考虑了存在绿色环保市场、制造商竞争和产品生命周期情形下的制造商定价问题。Debo等基于消费者偏好建立了无限周期的利润最大化模型[12]。Ferrer等研究了垄断竞争和多普勒竞争环境下,新品和再制造品无差异时两个、多个和无限多个产品生命周期下的定价策略,给出当成本节约额小于一定阈值时的最优定价[13]。Ferrer等进一步考虑了再制造品和新品有明显差异条件下的两个和多个周期的定价策略[14]。谢家平引入消费者市场需求偏好函数,探讨单一垄断厂商应该如何制定两期和无限期最优的产量-价格策略[15]。黄永等建立了制造商竞争环境下两周期、多周期和无限周期的闭环供应链模型,讨论制造商的定价和生产策略[16]。Chen研究了两周期和多周期双渠道环境下垄断制造商的定价策略,提出了无约束的静态模型和两种有约束的动态模型[17]。
上述多周期模型主要针对一个垄断制造商或制造商竞争环境下的定价问题进行研究,而没有考虑引入零售商进行分销的情况,故在Ferrer等[13,14],黄永等[16]的研究基础上,引入零售商进行分销,研究多周期下制造商和零售商的定价和协调策略,并给出当再制造成本节约额大于一定阈值时的最优定价和生产策略,进一步拓展了其研究。
1 模型基本假设和描述
考虑由一个制造商和一个零售商和顾客构成的闭环供应链,制造商生产的产品由零售商进行销售,制造商直接从顾客手中回收废旧品。
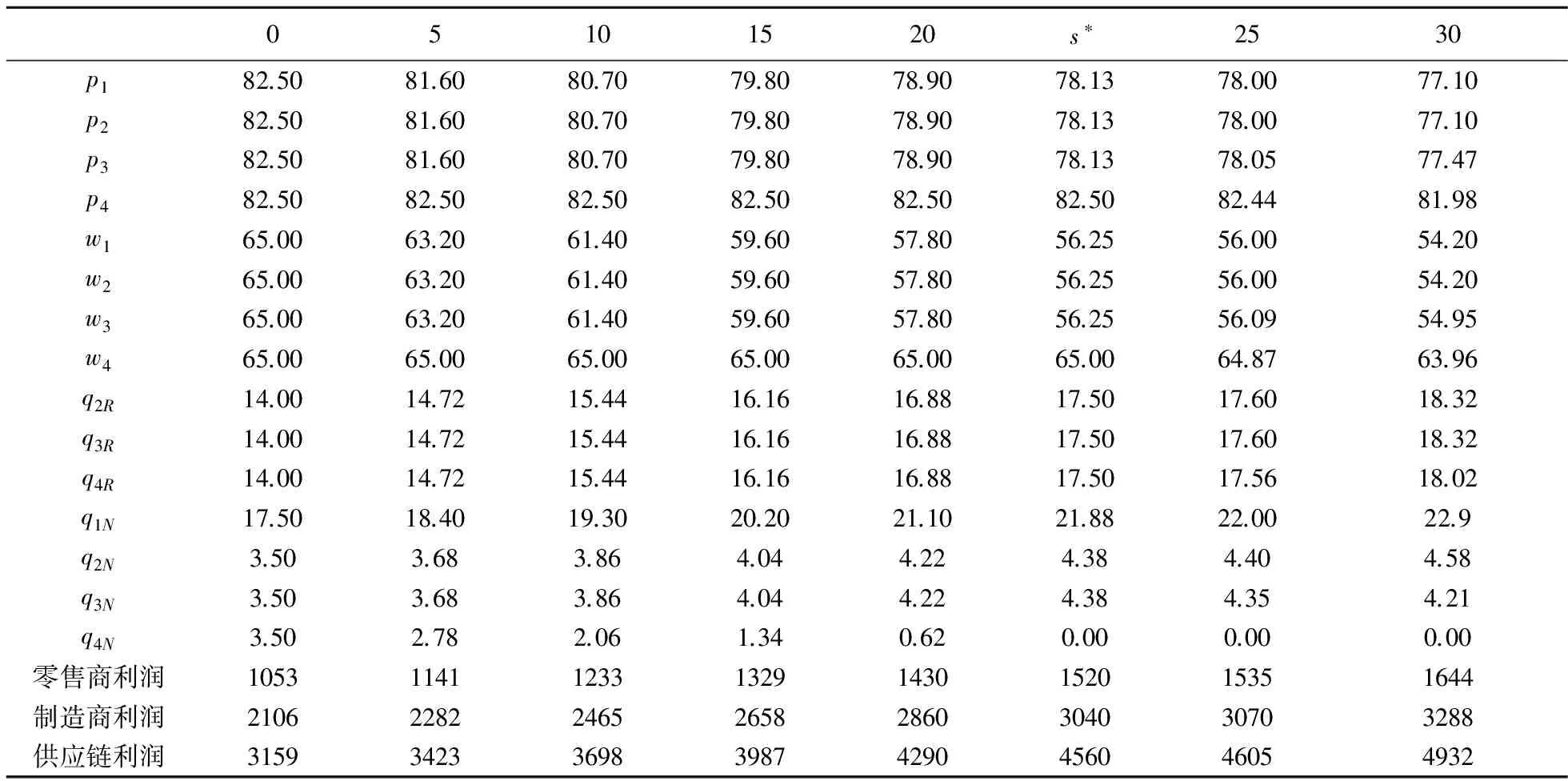
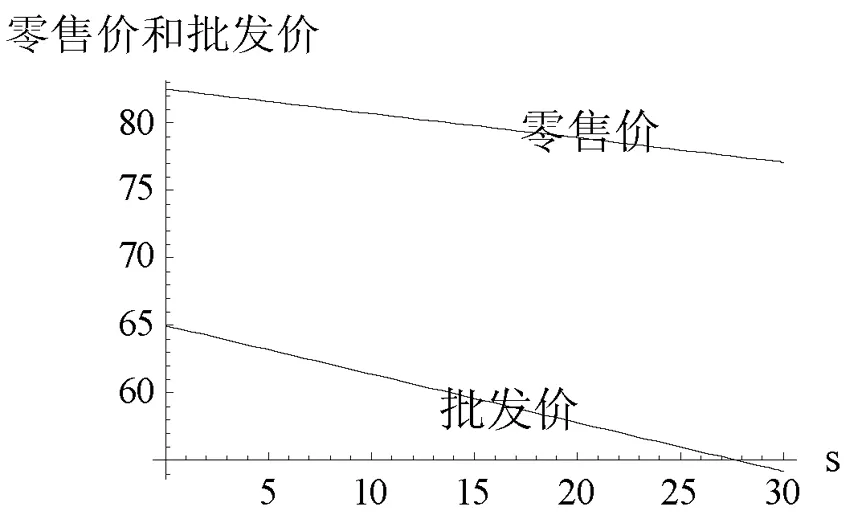
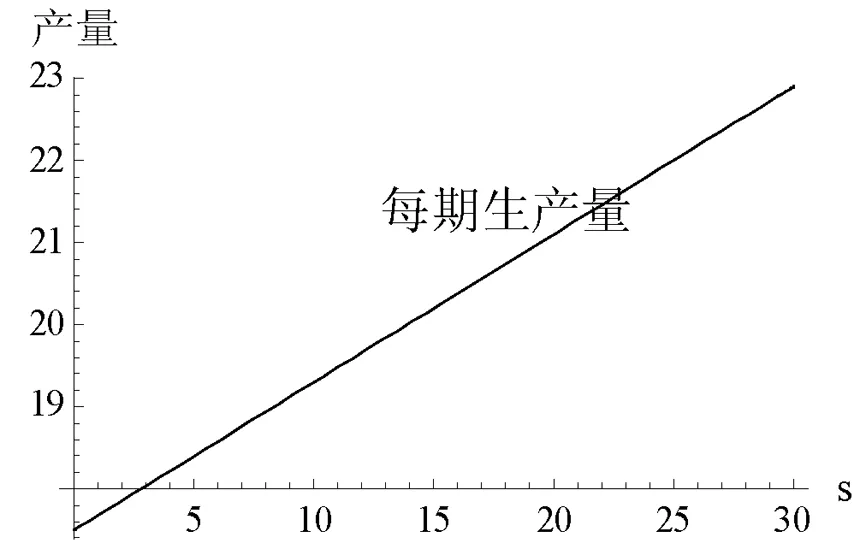
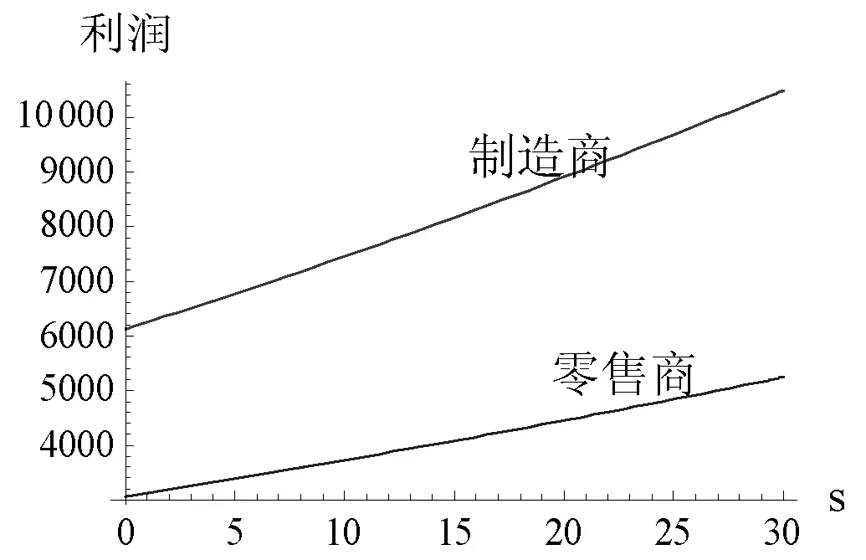
假设1 制造商生产的新品和再制造品是同质的,生产新品的单位成本为c,生产再制造品的单位成本节约额为s,故生产再制造品的单位成本为c-s,显然0 假设2pi表示零售商在第i期制定的零售价,wi表示制造商的批发价,qi,j表示制造商在第i期生产j产品的数量,其中,i=1,2……;J=N(新品),R(再制造品)或A(所有产品)。因此,可知qiA=qiN+qiR。在第一周期制造商只生产新品,从第二周期开始生产再制造品。假设产品的需求函数为qiA=Q-pi,其中Q为潜在市场规模,每周期都是定值[13]。 假设3 制造商为Stackelberg领导者,制造商和零售商均为风险中性且信息对称。 假设4 考虑利润的时间价值,设每期的贴现率为β(β≤1)。 制造商在第1周期只生产新品,在第2周期既生产新品也生产再制造品。制造商通过制定合适的批发价,生产合适数量的产品最大化其利润。制造商的决策问题为: (1) s.t.γq1A≥q2R (2) q2A≥q2R (3) 零售商通过确定合适的零售价最大化其利润。零售商的决策问题为: (4) 在分散决策模式下,制造商和零售商形成Stackelberg博弈,制造商是此博弈中的领导者,根据零售商的反应函数确定其最优批发价和生产量,而零售商零售价的确定取决于制造商的批发价和生产量。根据此博弈过程,可得定理1。 (2)当s≥s*时,制造商在第2周期只生产再制造品。零售商和制造商的最优决策为: (5) 求解K-T条件,由目标函数对q2R的导数可知λ+μ=βs,且λ0,μ0,因此可分以下三种情况进行讨论。 ①当λ=βs,μ=0时,制造商将回收的产品全部用于再制造,同时生产新产品。求解可得定理1前半部分所示结果。为了保证每期的生产量大于等于零,则必须满足s≤s*。 ②当λ=0,μ=βs-λ>0时,制造商将回收的产品全部用于再制造,且第2周期只生产再制造品。求解可得定理1后半部分所示结果。因λ*>0,μ*>0,故必须满足s>s*。 ③当λ=0,μ=βs时,只有当再制造的成本节约额s为零时才会成立。 定理1说明,如果再制造的成本节约额比较大,制造商在第2周期将不会生产新品,第2周期的生产量为第1周期生产量的γ倍,并将第1周期回收的产品全部用于再制造;如果再制造成本节约额比较小,制造商在第2周期既生产再制造品,也生产新品,并将回收的产品全部用于再制造。第1周期的零售价和批发价都比第2周期的低,生产量比第2周期的高。由此可以看出制造商和零售商可通过在第1周期制定比较低的批发价和零售价来提高第2周期的回收量,从而达到降低成本提高收益的目的。再制造条件下的零售价和批发价都小于或等于不进行再制造条件下的零售价和批发价,生产量大于或等于不进行再制造条件下的生产量。当再制造不能带来成本节约时(s=0),制造商和零售商在第1和第2周期的批发价和零售价相等,生产量也相等。 3.1 分散式闭环供应链 制造商在第1周期只生产新品,从第2周期开始到第M周期既生产新品也生产再制造品。制造商对每一周期制定合适的批发价,生产合适数量的产品最大化其利润。制造商的决策问题为: (6) s.t.γqk-1,A≥qk,R,k=2,…,M (7) qk,A≥qk,R,k=2,…,M (8) 零售商通过确定合适的零售价最大化其利润。零售商的决策问题为: (9) 通过计算制造商和零售商的均衡解,可得定理2。 定理2 令成本节约额s⦤s*,则零售商和制造商的最优决策为:零售商在第1周期到第M-1周期,都会采取相同的零售价,而不同于第M周期的零售价;制造商在第1周期到第M-1周期,都会采取相同的批发价,而不同于第M周期的批发价,在第1周期到第M-1周期生产的新品和再制造品数量之和相同,同时在每一周期生产的新品数量正好弥补了上一周期损失的产品数量,而不同于第M周期的生产量,即 第1周期: 第k(k=2,…,M-1)周期: 第M周期: 当s>s*且(Q-c)(1+βγ-γ-βγ3)+sβγ(1-γ-βγ3)≥0时,零售商和制造商的最优决策为:零售商在第1周期至第M-2周期都会采取相同的零售价,而不同于第M-1和第M周期的零售价;制造商将每一期回收的产品全部用于再制造,在第1周期至第M-1周期既生产再制造品,也生产新品,第M周期只生产再制造品,前M-2个周期的生产量相同,而不同于第M-1和第M周期的生产量,从第2周期开始至第M-1周期的再制造量相同,而不同于第M周期的再制造量,第2周期至第M-2周期的新品生产量相同,而不同于第M-1周期的再制造量,即 第1周期: 第k(k=2,…,M-2)周期: 第M-1周期: 第M周期: (1)当M=2时,定理1证明了定理2是成立的。 (2)假设当M=n-1时,定理2仍成立,令Π1,j代表制造商从第1周期到第j周期的利润之和,则有: Π1,n-1=max{maxΠ1,n-3+βn-3[(wn-2-c)qn-2,A+sqn-2,R]+βn-2[(wn-1-c)qn-1,A+sqn-1,R]} (10) s.t.γqn-3,A≥qn-2,R (11) γqn-2,A≥qn-1,R (12) qn-2,A≥qn-2,R (13) qn-1,A≥qn-1,R (14) 当Π1,n-3取最大值时,可得定理2所示的最优解。 (3) 当M=n时,制造商的所面临的决策问题为: Π1,n= max{maxΠ1,n-3+βn-3[(wn-2-c)qn-2,A+sqn-2,R]+βn-2[(wn-1-c)qn-1,A+sqn-1,R]+ βn-1[(wn-1-c)qn,A+sqn,R]} (15) s.t.γqn-3,A≥qn-2,R (16) γqn-2,A≥qn-1,R (17) γqn-1,A≥qn,R (18) qn-2,A≥qn-2,R (19) qn-1,A≥qn-1,R (20) qn,A≥qn,R (21) 构造制造商M周期的Langrangean函数如下: (22) 求解K-T条件,由目标函数对qn-1,R,qn,R的一阶导数可知λn-1和μn-1,λn和μn不可能同时为零,因此分以下四种情况进行讨论。 ④当λn-2=0或λn-1=0或λn=0,且λn-2,λn-1,λn,μn-2,μn-1,μn,中至少有一个不为零时,将会违反每期再制造生产量小于等于上一期回收量的约束条件,故不成立。 命题得证。 3.2 集中式闭环供应链 对于集中式闭环供应链,其决策问题变为[21]: (23) s.t.γqk-1,A≥qk,R,k=2,…,M (24) qk,A≥qk,R,k=2,…,M (25) 当s≤s*时,结果参考文献[13],当s>s*且(Q-c)(1+βγ-γ-βγ3)+sβγ(1-γ-βγ3)≥0时,求解可得定理3。 定理3 当s>s*且(Q-c)(1+βγ-γ-βγ3)+sβγ(1-γ-βγ3)≥0时,集中式闭环供应链的最优定价和生产量分别为: 第1周期: 第k(k=2,…,M-2)周期: 第M-1周期: 第M周期: 证明同定理2的证明,此处略。 当计划周期M趋向于无穷大时即为无限周期模型,因为考虑了利润的时间价值,未来利润的价值将会越来越小。由多周期模型可知,零售商和制造商除了第1周期以外的各个周期都会采取和第2周期相同的策略,即pi=p2,wi=w2,qi,R=q2R,qi,N=q2N(i=3,4,…)。 制造商的决策问题为: (26) s.t.γq1,A≥q2R (27) γq2A≥q2R (28) 零售商的决策问题为: (29) 通过求解,可得定理4。 定理4 零售商和制造商一直会采取和第1周期相同的零售价、批发价和生产量,同时在每一周期生产的新品数量正好弥补了上一周期回收中损失的产品数量。即 证明略。 和Ferrer等[13]的研究结果进行对比分析可以发现:分散式闭环供应链的零售价高于集中式闭环供应链的零售价,生产量低于集中式闭环供应链的生产量,闭环供应链利润也明显小于集中式闭环供应链的利润,存在双边效应,因此需要设计合理的契约来协调整个闭环供应链。 由于在闭环供应链中,供应链的收益不仅来源于其销售收入,同时也会从再制造成本节约中获得一定收益。因此,假设收益共享契约中,制造商共享零售商销售收入的比例为1-θ,同时制造商将其由再制造节约获得收益的η比例共享与零售商,则可得定理5。 证明 对于M(M≥2)周期闭环供应链,此时制造商的决策问题为: (30) s.t.γqk-1,A≥qk,R,k=2,…,M (31) qk,A≥qk,R,k=2,…,M (32) 零售商通过确定合适的销售价格最大化其利润。零售商的决策问题为: (33) 对于无限周期闭环供应链,此时制造商的决策问题为: (34) s.t.γq1,A≥q2R (35) γq2A≥q2R (36) 零售商的决策问题为: (37) 将零售商的利润函数对零售价进行求导并令其等于零,求得零售价和批发价之间的关系式,令其等于集中式供应链的零售价,即可得定理5。此时闭环供应链是协调的。 由定理5可知,制造商批发价的确定只和制造商共享零售商销售收入的比例θ相关,而和给予零售商的再制造收益比例η无关。但η的取值和θ一样都会影响到此共享契约的有效性。 设Q=100,c=30,β=0.9,γ=0.8,M=4,则计算可知s*=24.3056,当s=25,s=30时满足条件(Q-c)(1+βγ-γ-βγ3)+sβγ(1-γ-βγ3)≥0。此时零售商和制造商的零售价、批发价、生产量和利润随单位成本节约额变化的情况如表1所示。 表1 四周期分散式再制造闭环供应链定价和生产策略 从表1可知,当s≤s*时,除了最后一个周期(零售价和批发价和s无关,保持不变)以外,其他各个周期的零售价和批发价都随成本节约额s的增加而减少,生产量随成本节约额s的增加而增加,当s>s*且(Q-c)(1+βγ-γ-βγ3)+sβγ(1-γ-βγ3)≥0时,各个周期的零售价和批发价都随成本节约额s的增加而减少,生产量都随成本节约额s的增加而增加。最后一个周期出现差异的原因在于:当成本节约额s比较小时,最后一个周期制造商既生产新品也生产再制造品,生产总量和s无关;而当成本节约额s比较大时,最后一个周期制造商没必要生产新品,只生产再制造品,此时生产总量等于再制造量,和s相关,随s的增加而增加。在上述两种情况下,零售商和制造商的利润都随s的增加而增加。 图1、图2表示了无限周期零售价、批发价和生产量随成本节约额s变化的情况、图3表示无限周期零售商利润和制造商利润随成本节约额s变化的情况,从图中可知各个周期的零售价和批发价都随成本节约额s的增加而减少,生产量都随成本节约额s的增加而增加。零售商和制造商利润都随s的增加而增加。 图1 无限周期零售价、批发价随s的变化 图2 无限周期生产量随s的变化 当s=10时,在协调模式下,零售商利润为4390.82θ+753.16η,制造商利润为4930.82(1-θ)-753.16θ,且当2463.41≤4930.82θ+753.16η≤1232.7时,零售商和制造商的利润大于无契约下各自的利润,说明此契约是有效的。 当s=25时,零售商利润为6139.57θ+2144.99η,制造商利润为6139.57(1-θ)-2144.99η,且当1534.89≤6139.57θ+2144.99η≤3069.78时,零售商和制造商的利润大于无契约下各自的利润,说明此契约是有效的。此时制造商和零售商实现双赢。 当s=10制造商和零售商在有契约和无契约条件下的利润之差随θ,η的变化情况如图4所示,从图中可知零售商利润差随θ,η增加而增加,制造商利润差随θ,η增加而减少。当制造商共享零售商销售收入的比例增加时,即可将一部分再制造收益分配与零售商,使其利润大于无契约时的利润,从而实现供应链的协调,因此可通过调节θ和η的大小以协调供应链。 图3 无限周期制造商和零售商利润随s的变化 图4 有无契约下制造商、零售商的利润差随θ,η的变化 本文主要研究了第一周期只生产新品,从第二周期开始生产再制造品的两周期、多周期和无限周期中制造商和零售商的定价和生产策略及协调策略。结果表明:两周期情况下,存在成本节约额临界值,当成本节约额低于此值时,制造商既生产新品也生产再制造品;高于此值时,制造商只生产再制造品。第一周期的批发价和零售价都低于第二周期的批发价和零售价。多周期情况下,也存在一个成本节约额临界值,当成本节约额低于此值时,制造商既生产新品也生产再制造品,且每期再制造品量相等,除最后一个周期外,每期总生产量相等,批发价和零售价分别相等,都分别低于最后一期的批发价和零售价;当成本节约额高于此值且满足一定条件时,第一周期只生产新品,最后一个周期只生产再制造品,其他各期既生产再制造品也生产新品,且再制造品生产量相等,除最后两周期以外,其他各期的总生产量相等,批发价和零售价分别相等,都分别低于最后两期的批发价和零售价,最后一期的批发价和零售价最大。无限周期情况下,除第一周期外,每期都既生产再制造品也生产新品,且生产量相等,批发价和零售价每期都是相等的。通过引入收益共享契约制定合适的批发价和收益共享比率可以协调整个闭环供应链。因此,在有限周期情况下,制造商应通过在前期制定比较低的批发价,零售商制定比较低的零售价,以提高其生产量和销售量,从而使得后期的回收量增大,进一步达到降低自身成本,提高收益的目的。 本文忽略了再制造品和新品的差异性,并假设需求是确定的,因此再制造品和新品存在差异性,需求不确定,考虑回收成本等因素将是下一步的研究方向。 [1] Ferrer G, Ayres R U. The impact of remanufacturing in the economy[J]. Ecological Economics, 2000, 32(3): 413- 429. [2] Guide V D R. Production planning and control for remanufacturing: industry practice and research needs[J] Journal of Operations Management, 2000, 18(4): 467- 483. [3] Giutini R, Gaudette K. Remanufacturing: the next great opportunity for boosting US productivity[J]. Business Horizons, 2003, 46(6): 41- 48. [4] Ferguson M E, Toktay L B. The effect of competition on recovery strategies[J]. Production and operations management, 2006, 15(3): 351-368. [5] 徐峰,盛昭瀚,陈国华.基于异质性消费群体的再制造产品的定价策略研究[J].中国管理科学,2008,16(6):130-136. [6] Webster S, Mitra S. Competitive strategy in remanufacturing and the impact of take-back laws[J]. Journal of Operations Management, 2007, 25(6): 1123-1140. [7] Atasu A, Sarvary M, Van Wassenhove L N. Remanufacturing as a marketing strategy[J]. Management Science, 2008, 54(10): 1731-1746. [8] Chen J M, Chang C I. Pricing strategies for managing new and remanufacturing products in a closed-loop supply chain[J]. Information, 2012, 15(12): 5999- 6010 [9] 李新军.再制造成本随机分布和市场细分的生产优化模型[J].中国管理科学,2007,15(5):72-77. [10] 孙浩,达庆利.基于产品差异的再制造闭环供应链定价与协调研究[J].管理学报,2010,7(5):733-738. [11] 林欣怡,黄永,达庆利.两周期零售商竞争下的闭环供应链的定价和协调策略研究[J].运筹与管理,2013,22(2):28-33. [12] Debo L G, Toktay L B, Van Wassenhove L N. Market segmentation and product technology selection for remanufacturable products[J]. Management Science, 2005, 51(8): 1193-1205. [13] Ferrer G, Swaminathan J M. Managing new and remanufactured products[J]. Management Science, 2006, 52(1): 15-26. [14] Ferrer G, Swaminathan J M. Managing new and differentiated remanufactured products[J]. European Journal of Operational Research, 2010, 203(2): 370-379. [15] 谢家平,王爽.偏好市场下制造/再制造系统最优生产决策[J].管理科学学报,2011,14(3):24-33. [16] 黄永,孙浩,达庆利.制造商竞争环境下基于产品生命周期的闭环供应链定价和生产策略研究[J].中国管理科学,2013,21(3):96-103 [17] Chen J M, Chang C I. Dynamic pricing for new and remanufactured products in a closed-loop supply chain[J]. International Journal of Production Economics, 2013, 146(1): 153-160. Research on Pricing and Coordination Policies Based on Product Life-Cycle in Closed-Loop Supply Chain LU Rong-hua1,2, LI Nan1 (1.CollegeofEconomicsandManagement,NanjingUniversityofAeronauticsandAstronautics,Nanjing211106,China; 2.NanhangJinchengCollege,Nanjing211156,China) This study deals with the pricing and coordination policies based on product life-cycle in closed-supply chain consisting of one manufacturer and one retailer, where the manufacturer makes and supplies all-new products in the first period and uses returned cores to offer remanufactured products, along with the new ones, in the subsequence periods until the end of product life-cycle. We build a decentralized model in two-period, multi-period and infinite planning horizons and a centralized model in multi-period and characterize the optimal pricing and manufacturing strategy for the manufacturer and the retailer. The result suggests that in the two-period setting the manufacturer and the retailer should make different wholesale price, sales price and production quantity according to different cost savings, and in the multi-period setting the manufacturer and the retailer should adopt the same pricing and manufacturing strategies except the first and the last period with the low cost savings and adopt the same pricing and manufacturing strategies except the first period and the last two periods with the high cost savings, and in the infinite-horizon setting the manufacturer and the retailer should make the same pricing and manufacturing strategies except the first period. The manufacturer and the retailer should make lower price in the earlier periods to provide cores that are essential for the low cost production in the later periods. The whole closed-loop supply chain can be coordinated with revenue sharing contract. A numerical example is given to prove the conclusions above. closed-loop supply chain; product life-cycle; pricing policy; contract coordination 2013-12-19 江苏高校哲学社会科学研究项目(2015SJD040) 卢荣花(1983-),女,安徽萧县人,博士生,讲师,研究方向:供应链管理等;李南(1956-),女,重庆人,博导,教授,研究方向:供应链管理,项目管理理论与应用等。 F252 A 1007-3221(2015)06- 0112- 09 10.12005/orms.2015.02022 两周期分散决策模型
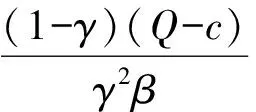
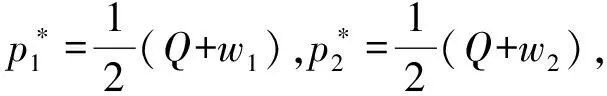
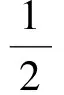
3 多周期模型
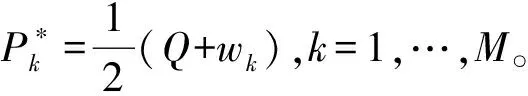
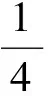
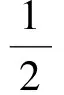
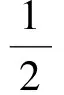

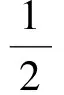


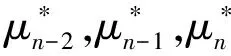

4 无限周期分散决策模型

5 协调机制
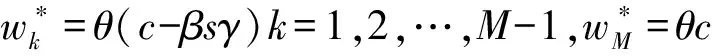

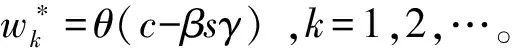
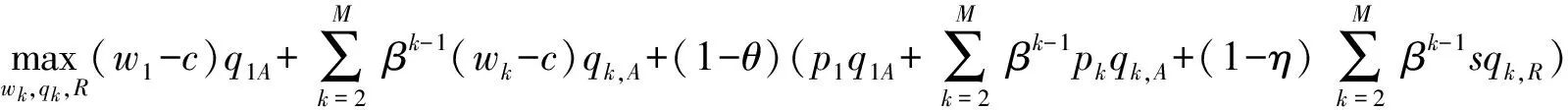

6 算例

7 结语

