信用期下时滞变质品供应链库存和定价的Stackelberg均衡策略
董坤祥, 侯文华, 陈宗泽, 丁慧平,3
(1.南开大学 商学院,天津 300071; 2.爱荷华大学 管理科学系,美国 爱荷华州 IA 52242; 3.青岛农业大学 经济与管理学院,山东 青岛 266109)
信用期下时滞变质品供应链库存和定价的Stackelberg均衡策略
董坤祥1, 侯文华1, 陈宗泽2, 丁慧平1,3
(1.南开大学 商学院,天津 300071; 2.爱荷华大学 管理科学系,美国 爱荷华州 IA 52242; 3.青岛农业大学 经济与管理学院,山东 青岛 266109)
在允许缺货和考虑资金机会成本情况下,根据时滞变质品的基本库存模型,分别构建了信用期下供应商为领导者(SL)和零售商为领导者(RL)的Stackelberg博弈模型。通过分析SL和RL下的Stackelberg博弈模型唯一均衡解,得到两个模型中均衡解的解析表达式。最后,根据数值算例分析得出:(1)在SL供应链中信用期并不总使整个供应链协调,然而在RL供应链中信用期的协调效果较好;(2)延长信用期或增加零售价格均能刺激零售商多订货;(3)在两个模型中,零售价格均随变质时刻递增,且整条供应链达到Pareto改进;(4)SL中供应商变动信用期与RL中零售商变动价格相比,SL供应链收益更高;而当信用期和价格固定,其他参数变动时,RL供应链收益更大。
库存;信用期;时滞变质品;Stachekelberg博弈
0 引言
据来自物流行业协会的数据显示,我国每年收购的1.3亿吨粮食中有1900万吨受到损失,其中因库存和运输中的损失达1000万吨,约占流通中粮食总量的10%;另外我国苹果年产量约1800万吨,在运输环节中的损耗率仅有1%~2%,而在贮存过程中损失达300万吨,相当于总产量的20%,这些腐烂损耗几乎可以满足近两亿人口的基本营养需求。此外,我国粮油因变质造成的损失约15%、蛋类约15%、肉类约3%,加上食品的等级间隔、运输及加工损耗,每年造成的经济损失约上千亿元。诸如此类农副产品具有在库存过程中出现损坏、腐败、干燥和蒸发等导致其原始可用性降低甚至消失特性的产品称为易逝品。易逝品可以分为两类:第一类是即逝品,即产品入库即变质(例如,挥发剂等化学类产品);第二类是时滞变质品,即变质品具有一定的保质期(例如,水果,蔬菜,面包,时尚服装,电子类消费品等)。Ferguson和Ketzenberg[1]通过调查发现各类产品在销售过程中因变质或者损耗的损失达15%,而在我国水果蔬菜等农产品供应链流通环节因腐烂变质或贬值处理高达20%~30%。因此,对于变质品的研究有着国计民生的意义,并引起了学术界的高度关注。
研究中发现,零售商因需要投入大量的运营资金保存和处理已经变质的产品,而导致订货资金短缺。为了激励零售商加大订货量的同时减少运营资金的投入,供应商会向零售商提供一定的信用期期限。现已有学者对如何协调信用期和订货进行了相关研究。Wu等[2]首次提出时滞变质品的概念,并建立了信用期下不允许缺货且需求固定的时滞变质品库存模型;Ouyang[3]等进一步扩展了Wu的模型,构建了考虑生命周期的时滞变质品的库存模型,并优化了不同情境下最优解的求解算法;然后,Chung[4]进一步完善了Ouyang的研究,通过比较信用期、变质时刻和订货周期的大小将问题划分为6种不同的情形,并构建了相应的模型及求解;Geetha和Uthayakumar[5]在Ouyang模型的基础上首次构建了允许缺货的时滞变质品库存模型。后来,一些学者对时滞变质品库存的模型和情境进行不同方面的拓展,例如,变质前后的两阶段定价[6],需求变化[7~12],变质率的分布以及影响因素[12,13]等。
以上学者的研究视角多是合作决策或单独决策下构建相关模型,尚未考虑供应链中供应商和零售商因地位不同对决策的影响。目前,在采用信用期策略的供应链中,考虑决策者地位建模时多假设供应商为主导者,例如,Kouvelis和Zhao[14]的报童模型,Zhou等[15,16]以及胡劲松和胡玉梅[17]的EOQ模型,Shi和Zhang[18]以及Chern等[19]考虑风险的拓展EOQ模型。上述学者通过对模型的求解发现,采用信用期策略能够增加供应链的收益,且能够实现供应链协调。此外,在变质品供应链中考虑决策者地位文献主要有:Xiao和Xu[20]在供应商为领导者的变质品供应链中,探讨了VMI策略下,价格和服务水平两个内生变量之间的关系以及对供应链绩效的影响,发现供应链绩效随着市场规模、价格灵敏度、变质率和供应商成本以及服务投资效率的增大而增大;随后,许甜甜和肖条军[21]进行了延续性研究,将文献[20]中的变质品拓展为时滞变质品,并讨论了数量折扣下集中和分散情况下的均衡解,得到产品变质时刻和价格之间成反比关系,还发现生产商向零售商提供的最优批发价格折扣随着生产商的生产成本和库存持有成本增加而增加。
当前,供应链的主导权从上游的供应商逐渐向中下游零售商转移,以零售商为领导者的供应链研究日益受到关注:徐贤浩和聂思玥[22]研究发现在零售商主导的变质品供应链中,零售商通过竞价手段将供应商的产品订购价格压制在比较低的水平;赵道致和吕昕[23]将公平偏好引入传统VMI模型揭示了零售商为主导供应链中公平偏好起作用的边界条件。一些学者对SL和RL两种供应链结构的效率进行了对比发现,在VMI[24]、需求受价格和广告影响[25]以及闭环[26]等供应链中,零售商为领导者的供应链的效率更高。
基于上述文献的分析发现,现有文献尚未讨论和对比信用期下不同领导者的Stackelberg博弈对时滞变质品的库存及定价产生的影响。因此,本文基于Stackelberg博弈分别构建了供应商为领导者和零售商为领导者两种供应链中考虑信用期的时滞变质品供应链库存模型,并对数值结果进行了讨论。与已有文献的不同体现在以下两方面:
一方面,在模型构建上:以时滞变质品为研究对象,首次在考虑信用期的时滞变质品供应链中构建供应商为领导者(SL)和零售商为领导者(RL)的Stackelberg博弈模型;其次,前人多采用最优算法求解,本文则运用牛顿—莱布尼茨方法化简模型,并给出不同情形下均衡解的解析表达式。
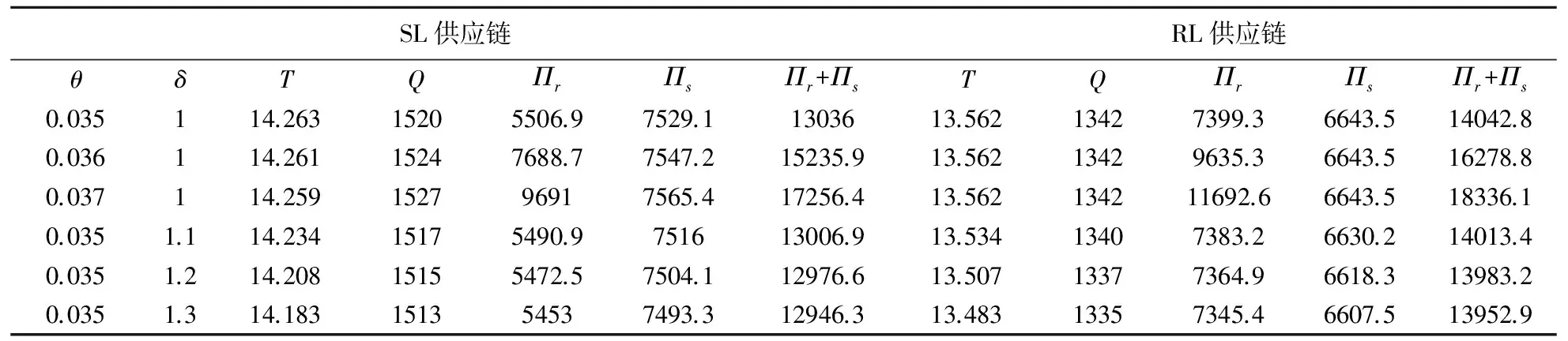
另一方面,在结论上与既存信用期下变质品供应链文献的不同:(1)现有文献认为信用期可以同时增加买卖双方的总收益,而本文发现,在SL供应链中,当0≤M 图1 时滞变质品库存水平及不同信用期下的情形 本文考虑零售商向供应商采购单一时滞变质品,供应商为鼓励零售商多订货而给予零售商一定的信用期。模型中产品的生产率无穷大,产品生产后在供应商库存中滞留一定时间τ,然后运往零售商处。零售商的库存变化时间序列为:首先,零售商采购Q单位的产品,且期初零售商的库存量为Im;产品保质期为τ+td;td为产品变质时刻,在[0,td]时间段内产品未变质,零售商库存的减少仅依赖于外部需求,用I1(t)表示;t0为库存为零的时刻,在[td,t0]时间内产品开始变质,零售商的库存量因外部需求和产品变质而减少,用I2(t)表示;T为零售商的订货周期,在[t0,T]时间内产品缺货,用I3(t)表示。由图1可知,td,t0,T和信用期M之间的大小关系有:(1)0≤M 1.1 参数符号 θ:产品的变质率;D:单位时间的需求率;Ip:单位资金费用率;Ie:利息率;cd:单位变质成本;cs:单位缺货成本;c0:单位机会损失成本;w:供应商单位售价,及零售商的单位批发价;c:供应商的原材料采购单价;p:零售商单位售价;As:供应商一次订货成本;Ar零售商一次订货成本;hs:供应商单位库存持有成本;hr零售商单位库存持有成本。 1.2 假设条件 假设1 零售商订货提前期为零; 假设2 产品不会在供应商处变质; 假设3 产品的运输时间为0; 假设4 产品一旦产生变质即失去全部效用; 假设5 允许缺货,与文献[8]、[9]和[27]假设相同,产品缺货情况下需求累积函数B(x)=ke-δx(0 1.3 模型构建 根据图1,建立库存水平的微分方程: (1) 根据边界条件I1(0)=Im,I1(td)=I2(td)和I2(t0)=I3(t0)=0求解微分方程(1)得: (2) 将t=T带入I3(t)得累积需求量为: (3) 由于I1(0)=Q-Im,因此,零售商的订货量为: (4) 根据图1,得到供应商的收益模型为: Πs=wQ-cQ-HsQτ-cIpQτ-wIpQM-As (5) 其中,wQ为供应商的销售收入,cQ为供应商的采购成本,hsτQ为供应商的库存持有成本,cIpQτ为供应商的库存机会成本,wIpQM为供应商提供信用支付的机会成本,As为供应商每次发生的订货成本。 基于以上描述,零售商在三种情形(0≤M (6) 2.1SL供应链Stackelberg博弈模型 根据(5)式和(6)式,构建SL供应链Stackelberg博弈模型,如下: (7) (1)当0≤M 命题1的证明均在附录中给出。 从命题1可以得到Stackelberg博弈下SL供应链中相关推论: 推论3 订货周期T*随累积需求参数δ,变质率θ和信用期M(M 2.2RL供应链Stackelberg博弈模型 (8) 命题2证明与求解过程与命题1相同。 从命题2可知,在RL供应链中具有与SL供应链不同的性质: 推论4 在RL供应链中产品变质时刻td与变质率θ无关。 为了说明构建模型的有效性,使用一组相同的数据验证这两个模型。既可以观察参与者收益的连续变化,也可以针对不同的情形作出对比分析。参数设置为:D=100,hr=0.5,hs=0.1,θ=0.035,Ip=0.02,Ie=0.013,c=5,w=cd=10,cs=3,c0=1,B(x)=e-x,Ar=500,As=50,τ=0.1。用Mathematica 8.0对模型进行计算,所得结果如表1所示。 表1 两种Stackelberg博弈模型在不同情形下的数值结果 注:SL表示供应商为领导者的供应链;RL表示零售商为领导者的供应链。 通过分析表1,可以得出以下结论: (1)SL的Stackelberg博弈分析: 根据假设和πs>0的约束,可以等到不同情形下信用期的取值范围:(i)当0≤M 当0≤M 通过讨论可知,在SL的时滞变质品供应链中,并不是在任何情形下增加信用期均可增加供应链各成员的收益。由于处于领导地位的供应商追求其自身利益的最大化,此时供应商最优决策是不向零售商提供信用期。即使双方订立相关契约,供应商仅会在0≤M (2)RL的Stackelberg博弈分析: 由表1可以,前两种情形在现实中并不可取,因此零售商的决策只会在第三种情形作出选择。此时,由于高价格带来高收益,零售商则会选择提高价格。但是,较高的价格使零售商的竞争力下降,为了权衡增加收益与竞争力下降,零售商则会要求供应商在t0≤M范围内提供尽可能长的信用期。 (3)在两个Stackelberg博弈模型中,当供应商增加信用期或零售商提高零售价格,在领导者获得Stackelberg均衡解的基础上零售商总会增加订货量(与Panos和Zhao,2012结论相同)。同时,如果零售商增加销售价格,供应链则会在每种情形下均可达到Pareto改进(见表1和表2)。 表2 供应商为领导者时,当M=1时,不同p下的数值分析 由表2可知,当供应商提供固定信用期(M=1)时,零售价格越高,双方受益越大即,提高售价可使双方达到Pareto改进。同时,td,t0,T和Q的最优值随p的增加而递增。与在SL供应链中其他情形下结论相同。 为了进一步了解博弈双方在决策方面的相互影响,现讨论SL供应链中信用期M和售价p对各方收益的灵敏度分析,结果如图2所示。 图2 供应商为领导者时,信用期变化对供应链收益的影响 从图2(a)可以看出,在SL情况下,当0≤M 图3 零售商为领导者时,供应链的Pareto改进 从图3得到RL供应链中以下结论: (1)零售商增加售价,供应链达到Pareto改进; (2)随着信用期的增加,供应商的收益基本不变; (3)零售商的收益增长率大于供应商的收益增长率,即零售商总会在信用期中收益。 两种供应链结构下收益的对比: (2)SL的时滞变质品供应链中不同情况下双方收益的变化率不同,如图2(a)中双方收益均下降的情况下,零售商收益下降速度慢,而图2(b)中零售商的收益增加,供应商的收益减少,且零售商增加的收益大于供应商的损失,即供应链的总收益增加。如表1和图3所示,在RL供应链中双方收益均增加,且零售商的增加率大于供应商的增加率。 综上所述,无论在哪种类型的供应链中零售商总能占据有利地位(收益下降时,减少得最少;收益增加时,增加得最快)。 产品的变质率θ影响产品库存的变化,进而影响订货决策;产品累积需求参数δ则通过影响累积需求产生的利润和缺货损失来影响零售商的决策。为探究参数θ和δ对两种不同的供应链的决策影响有何不同,本文对t0≤M,且参数为M=15和p=40条件下,做如下灵敏度分析。 表3参数θ和δ的灵敏度分析 从表3中可以看到如下结论: (1)变质率θ的影响:在SL的情况下,当θ增加时,零售商的订货周期缩短,订货量和收益却增加。这是因为,供应商提供的信用期足够大(t0≤M),弥补了零售商因多订货而产生的损失。同时,零售商通过缩短订货周期和增加订货量来应对因变质率增大而产生的产品库存不足。在零售商为领导者的情况下,由推论4可知θ与变量T和Q没有关系,但由参数设置以及式(6)得θ增加,持有成本HC减少,变质成本DC增加,且变化量ΔHC-ΔDC>0,故零售商收益增加。 (2)累积需求参数δ的影响:在两种供应链结构中均出现以下情形,当δ增加时,需求的累积量B(x)减少,缺货成本和机会成本均增加。为避免更大的损失,零售商减少订货量并缩短订货周期,进而导致整条供应链的收益下降。 (3)通过两种供应链下收益对比,与供应链中领导者可操控对应变量下结论不同,当双方均不能掌控M和p时,RL供应链收益更大。 时滞变质品供应链的库存控制可在一定程度上减少不必要的库存浪费,供应商通过提供信用期融资来降低零售商库存资金的投入。因此,库存控制和信用期融资问题一直受到零售业和学术界的高度关注与重视。目前时滞变质品的相关文献从多集中决策或单独决策的时滞变质品供应链两个角度进行研究,忽略了现实生活中生产商和零售商在不同供应链中因实力地位不同而存在差异这一要素。本文考虑了供应商提供信用期,零售商确定售价下的库存订货策略,首先构建了外部需求固定,且允许缺货的SL的Stackelberg博弈模型和RL的Stackelberg博弈模型;其次,通过命题的形式证明了最优解的存在并求出其解析表达式;最后,通过数值计算和分析发现:SL的Stackelberg博弈中,作为决策者的供应商不会延长提供信用期,但零售商的决策者为了维持合作关系,而会增加订货量,此时若td≤M 本文在模型构建中假设外部需求是固定的,但是变质品具有易变质、存储费用高、外部需求波动大等特点,因此将来的研究可以从不确定需求,变质率随时间变化或考虑多种时滞变质品协同订货,以及供应商为延长保质期付出努力等方面进行深入研究。此外,变质品的订货规模有大、小之分,不同规模的订货方式模型构建和影响产品变质的因素也各不相同,因此,后续研究也可比较不同订货规模的库存订货策略。 [1] Ferguson M E, Ketzenberg M E. Information sharing to improve retail product freshness of perishables[J]. Production and Operations Management, 2006, 15(1): 57-73. [2] Wu K S, Ouyang L Y, Yang C T. An optimal replenishment policy for non-instantaneous deteriorating items with stock-dependent demand and partial backlogging[J]. International Journal of Production Economics, 2006, 101(2): 369-384. [3] Ouyang L Y, Wu K S, Yang C T. A study on an inventory model for non-instantaneous deteriorating items with permissible delay in payments[J]. Computers and Industrial Engineering, 2006, 51(4): 637- 651. [4] Chung K J. A complete proof on the solution procedure for non-instantaneous deteriorating items with permissible delay in payment[J]. Computers and Industrial Engineering, 2009, 56(1): 267-273. [5] Geetha K V, Uthayakumar R. Economic design of an inventory policy for non-instantaneous deteriorating items under permissible delay in payments[J]. Journal of computational and applied mathematics, 2010, 233(10): 2492-2505. [6] Tsao Y C. Two phase pricing and inventory management for deteriorating and fashion goods under trade credit[J]. Mathematical Methods of Operations Research, 2010, 72(1): 107-127. [7] Musa A, Sani B. Inventory ordering policies of delayed deteriorating items under permissible delay in payments[J]. International Journal of Production Economics, 2012, 136(1): 75- 83. [8] Maihami R, Nakhai K I. Joint pricing and inventory control for non-instantaneous deteriorating items with partial backlogging and time and price dependent demand[J]. International Journal of Production Economics, 2012, 136(1): 116-122. [9] Maihami R, Nakhai K I. Joint control of inventory and its pricing for non-instantaneously deteriorating items under permissible delay in payments and partial backlogging[J]. Mathematical and Computer Modelling, 2012, 55(5- 6): 1722-1733. [10] Soni H N, Patel K A. Joint pricing and replenishment policies for non-instantaneous deteriorating items with imprecise deterioration free time and credibility constraint[J]. Computers & Industrial Engineering, 2013, 66(4): 944-951. [11] Soni H N. Optimal replenishment policies for non-instantaneous deteriorating items with price and stock sensitive demand under permissible delay in payment[J]. International Journal of Production Economics, 2013, 146(1): 259-268. [12] Shah N H, Soni H N, Patel K A. Optimizing inventory and marketing policy for non-instantaneous deteriorating items with generalized type deterioration and holding cost rates[J]. Omega, 2013, 41(2): 421- 430. [13] Dye C Y. The effect of preservation technology investment on an on-instantaneous deteriorating inventory model[J]. Omega, 2013, 41(5): 872- 880. [14] Kouvelis P, Zhao W. Financing the newsvendor: supplier vs. bank, and the structure of optimal trade credit contracts[J]. Operations Research, 2012, 60(3): 566-580. [15] Zhou Y W, Zhong Y G, Li J C. An uncooperative order model for items with trade credit, inventory dependent demand and limited displayed-shelf space demand and limited displayed-shelf space[J]. European Journal of Operational Research, 2012, 233(1): 76- 85. [16] Zhou Y W, Zhou D. Determination of the optimal trade credit policy: a supplier-Stackelberg model[J]. Journal of the Operational Research Society, 2012, 64(7): 1030-1048. [17] 胡劲松,胡玉梅.模糊环境下考虑缺货和延期支付Stackelberg均衡策略[J].管理工程学报,2011,25(2):87-94. [18] Shi X J, Zhang S M, Trade credit: the interaction of financing, marketing, operations, and risk behavior[J]. Review of Management Science, 2014, 8(2): 225-248. [19] Chern M S, Pan Q, Teng J T, et al. Stackelberg solution in a vendor-buyer supply chain model with permissible delay in payments[J]. International Journal of Production Economics, 2013, 144(1): 397- 404. [20] Xiao T J, Xu T T. Coordinating price and service level decisions for a supply chain with deteriorating item under vendor managed inventory[J]. International Journal of Production Economics, 2013, 145(2): 743-752. [21] 许甜甜,肖条军.基于数量折扣的时滞变质物品库存协调模型[J].系统工程理论与实践,2013,33(7):1690-1698. [22] 徐贤浩,聂思玥.零售商主导的短生命周期产品供应链订货策略[J].管理科学学报,2009,12(4):83-93. [23] 赵道致,吕昕.零售商主导供应链中考虑供应商公平偏好的VMI模型[J].运筹与管理,2013,22(3):45-52. [24] Almehdawe E, Mantin B. Vendor managed inventory with a capacitated manufacturer and multiple retailers: retailer versus manufacturer leadership[J]. International Journal of Production Economics, 2010, 128(1): 292-302. [25] Naimi S A, Mozafari M, Karimi B. Manufacturer-retailer supply chain coordination: a bi-level programming approach[J]. Advances in Engineering Software, 2012, 45(1): 144-152. [26] 易余胤.不同主导力量下的闭环供应链模型[J].系统管理学报,2010,19(4):389-396. [27] Abad P L. Optimal pricing and lot-sizing under conditions of perishability and partial backordering[J]. Management Science, 1996, 42(8): 1093-1104. Inventory and Price Stackelberg Equilibrium Policies of Non-instantaneous Deteriorating Items Supply Chain with Trade Credit DONG Kun-xiang1, HOU Wen-hua, CHEN Zong-ze2, DING Hui-ping1,3 (1.BusinessSchool,NankaiUniversity,Tianjin300071,China; 2.DepartmentofManagementSciences,UniversityofIowa,Iowacity,IA52242,USA; 3.SchoolofEconomicandManagement,QingdaoAgricultureUniversity,Qingdao, 266019,China) Based on the inventory model of non-instantaneous deteriorating items, two kinds of inventory models(supplier as the leader-SL & retailer as the leader-RL), by considering shortage and cash time cost, based on Stackelberg game for non-instantaneous deteriorating items under trade credit are developed. The equilibrium solutions of the two models are obtained by analyzing the Stackelberg game model. Finally, our results of the numerical examples show: (1)Trade credit is not always an appropriate way to coordinate the whole supply chain in SL, while it is much better for the supply chain with the RL; (2)And prolonging the trade credit or improving sales price can increase the order quantity; (3)The sales price is increasing with deterioration time, and the whole chain gets the Pareto improvement in both SL and RL models; (4)Comparing supplier changes the trade credit period in SL with changing the sale price in RL, the profit of SL is much higher when changing the trade credit period in SL; however, when the trade credit period and price are fixed, the profit of RL is much higher. inventory; trade credit; no-instantaneous deteriorating items; stackelberg game 2013-12-21 国家自然科学基金资助项目(71071080);国家社科基金资助项目(15BGL074) 侯文华(1964-),通讯作者,男,河北邢台人,教授、博士生导师,研究方向为服务外包、供应链协调等;董坤祥(1988-),男,山东陵县人,博士研究生,研究方向为供应链金融,服务外包;陈宗泽(1986-),男,黑龙江哈尔滨人,博士研究生,研究方向为动态网络定价;丁慧平(1976-), 女,山东日照人,讲师,博士研究生,研究方向:电子商务外包。 C931 A 1007-3221(2015)06- 0076-10 10.12005/orms.2015.0198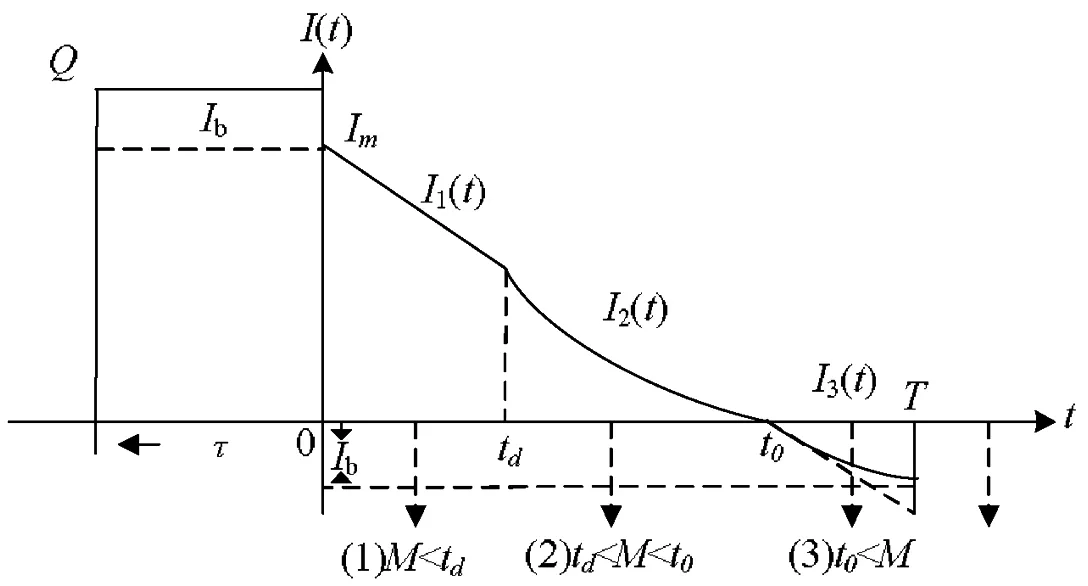
1 基本模型
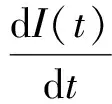
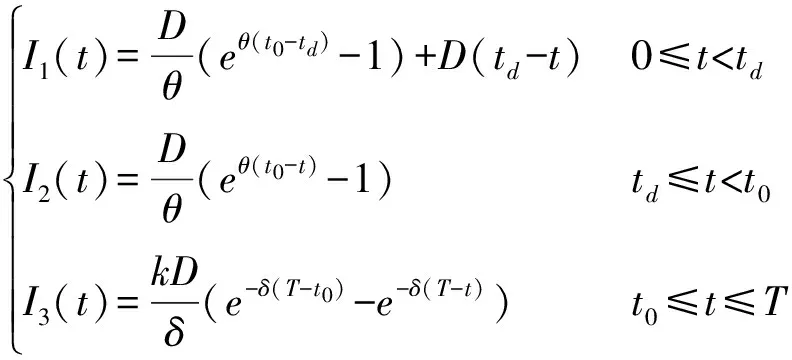
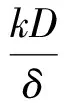
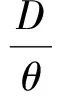
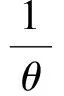
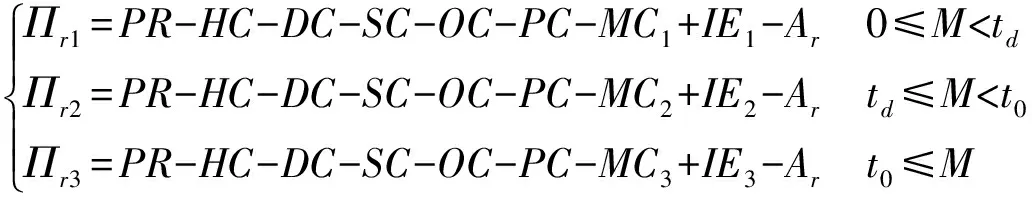
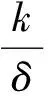
2 Stackelberg博弈模型
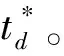
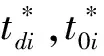
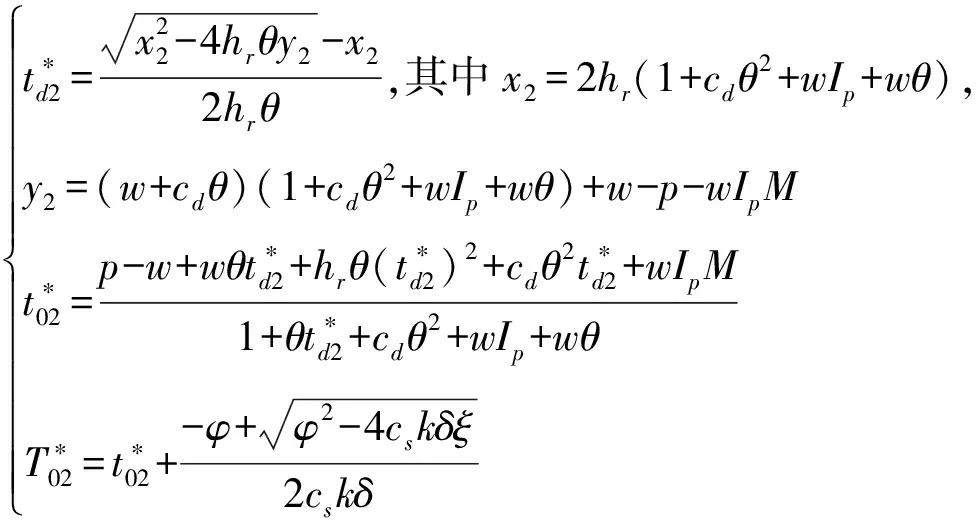
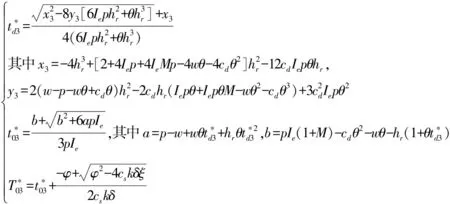
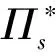
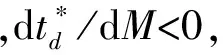
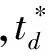
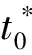
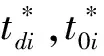
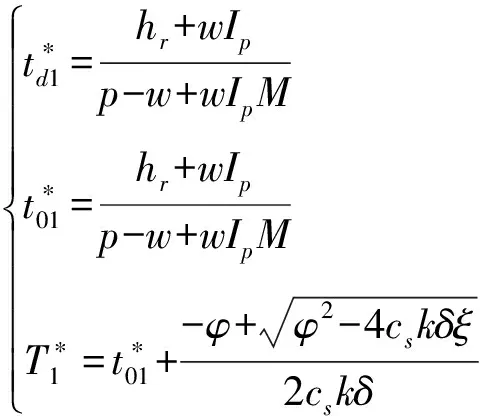
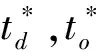
3 数值算例分析
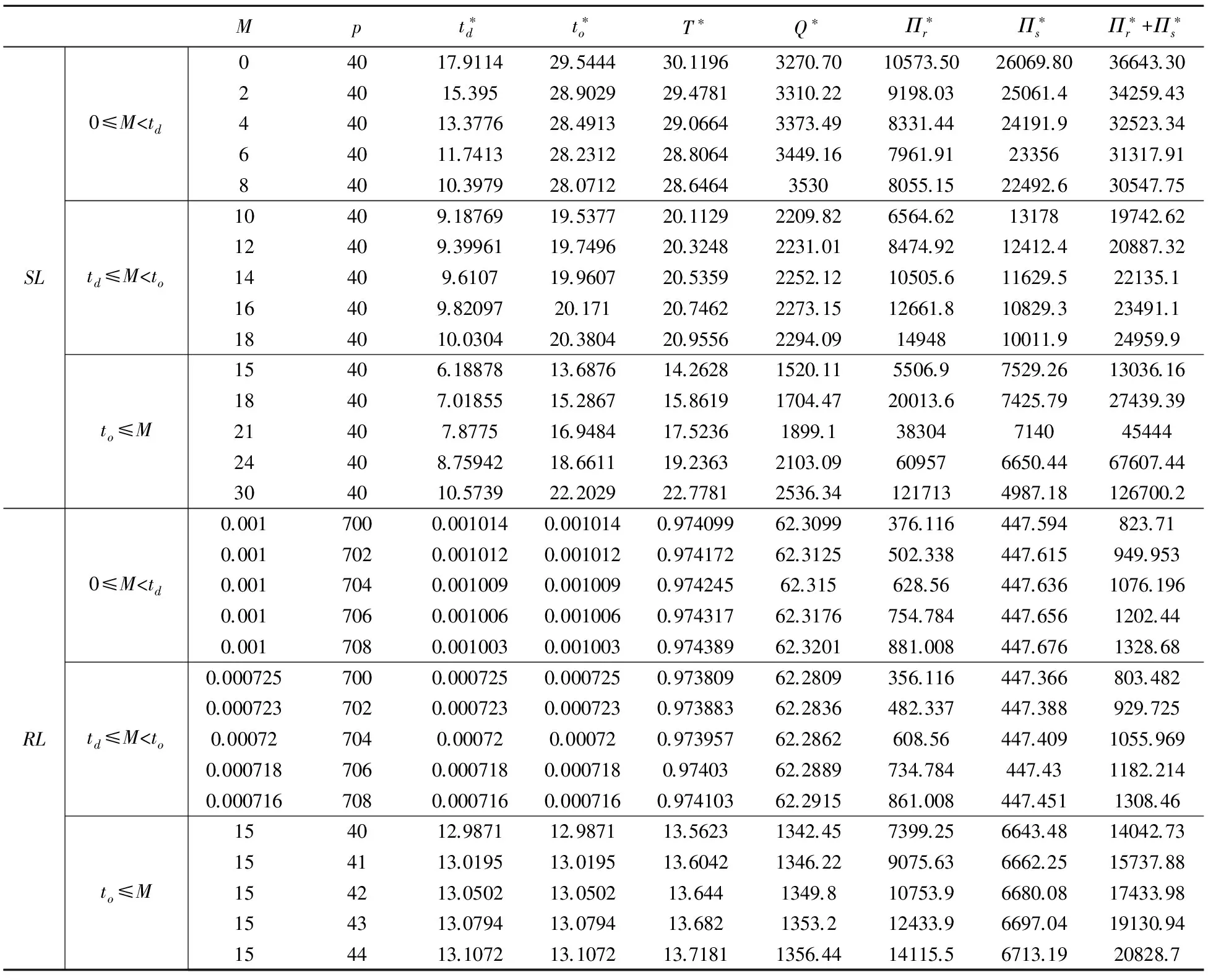

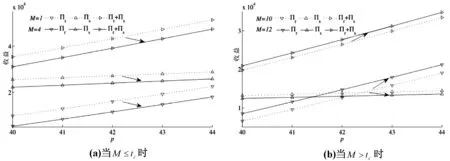
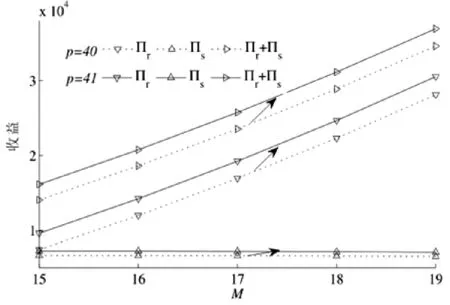
4 结束语

