带时间窗口的超市物流配送不确定规划模型
吴攀峰, 刘慧清, 彭 锦
(1.湖北大学 数学与统计学学院,湖北 武汉 430062; 2.黄冈师范学院,不确定系统研究所,湖北 黄冈 438000)
带时间窗口的超市物流配送不确定规划模型
吴攀峰, 刘慧清, 彭 锦
(1.湖北大学 数学与统计学学院,湖北 武汉 430062; 2.黄冈师范学院,不确定系统研究所,湖北 黄冈 438000)
主要研究了不确定环境下带时间窗口的超市物流配送问题。假设超市的日需求量是不确定变量,在配送过程中车辆的行驶时间也为不确定变量。为了最小化配送过程中车辆行驶时间,建立了不确定机会约束模型。然后应用不确定变量的运算法则对模型进行等价转化,并为求解模型设计了算法。最后给出了一个数值算例来说明模型的实际应用。
物流配送;时间窗口;不确定变量;机会约束
0 引言
物流是现代社会企业价值创造和价值实现的关键环节,是企业生产经营的生命线之一。物流配送是实现物流的基础体现。随着物流的快速发展,物流配送在整个物流系统中的作用越来越显著。在物流配送过程中,配送中心一般要向多个客户配送,在各客户对配送中心服务满意的情况下,让配送成本最小是配送中心所关注的问题。这里的配送成本主要考虑的是配送车辆在行驶过程中的能源消耗,在一定程度上,车辆的行驶时间与能源消耗正相关。因此缩短配送时间已成为当今一个重要的研究课题。
在物流配送过程中,存在很多不确定信息。需求商品特征的不确定性、需求客户时间的不确定性、道路的不确定性和配送车辆的不确定性等都会影响配送效率。而配送时间是影响配送效率的首要因素之一。在近些年里,从配送时间对物流配送的影响方面,一些学者对物流配送进行了研究,并建立了物流配送模型。贺国先和刘凯[1]充分考虑所运载货物交付时间的紧迫性,构造了满载约束的数学期望模型。李延晖等[2]在基于时间竞争的环境下,建立了多源配送系统随机模型。王绍仁和马祖军[3]针对震后紧急响应阶段路网中断和救援物资需求不确定性,建立了航空物流中的随机定位路线安排问题模型。张乐诚和杨信丰[4]考虑城市物流配送中道路交叉口时间延误的影响,构造了有车辆载重、多车型和时间窗约束的随机机会约束规划模型。
上述学者都采用的是概率论的方法对配送时间进行研究,然而利用概率理论的基本前提是得到的概率分布与实际频率非常接近。由于配送过程中的各种因素的不确定性,在实际情况下我们往往很难得到样本数据。当我们不能得到充足样本数据时,一般会向这方面的专家请教,请他们给出事件发生的信度。通常情况下,这个信度与概率测度在运算上有较大的差别。Liu[5]2007年提出了基于规范性、对偶性、次可加性和乘积测度公理下的不确定理论可以用来处理这种信度。作为不确定理论在实际生活中的重要应用,Liu[5]在不确定理论的公理化体系下提出了不确定规划[6],用于解决机器排序、车辆路径和工程进度等实际问题。近年来, 不确定规划作为一种数学工具被很多学者所应用。Zhang和Peng[7]研究了中国邮路问题,从不同的角度给出了三个不确定规划模型。Gao[8]根据不同的满意度建立了两个不确定规划模型来解决网络单设施选址问题。Ding[9]以粮食的质量、工厂建立费用作为不确定变量建立不确定规划来解决粮食供应链问题。Jiang[10]建立了不确定机会约束规划模型解决集装箱空箱调运问题。Rong[11]将储存成本、缺货成本、订购单位成本看作不确定变量构造了两个经济订货批量不确定规划模型。Zhang和Peng[12]提出α-最优指派的概念后建立了α-最优不确定规划模型来解决最优指派问题等。
本文在不确定环境下, 以超市的日需求量和配送过程中车辆的行驶时间为不确定变量,建立了以配送时间最短为目标的不确定规划模型, 并设计了一种算法对模型进行求解, 最后为了模型的实际应用给出了一个数值算例。
本文的结构框架如下:第一节简要介绍不确定理论的基础知识, 第二节描述了以超市的日需求量和车辆的行驶时间为不确定变量的物流配送问题, 且为解决此问题建立了不确定规划模型, 第三节利用不确定理论的基础知识将不确定规划模型转化为一般的数学模型, 并给出了模型的算法, 第四节给出了一个数值算例。最后对本文做了小结。
1 不确定理论基础知识
定义1 (Liu[5]) 设Γ是一个非空集合,L是Γ上的一个σ-代数,L中的每一个元素Λ称为一个事件。若L上的集函数M满足以下公理:
公理1(规范性) 对全集Γ,有M{Γ}=1;
公理2(对偶性) 对任意的事件Λ∈L,有M{Λ}+M{ΛC}=1;

定义1 (Liu[5]) 不确定变量ξ的分布函数Φ定义为Φ(x)=M{γ|ξ(γ)≤x},x∈R,它的反函数Φ-1称为不确定变量ξ的逆分布。

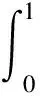
定理2 (Liu[5]) 设ξ和η是具有有限的期望值的两个独立的不确定变量。对于任意实数a和b, 我们有E[aξ+bη]=aE[ξ]+bE[η]。
定理3 (Liu[13]) 一个实值函数f(x1,x2,…,xn)被称为严格增的,若当xi≤yi,i=1,2,…,n时,有f(x1,x2,…,xn)≤f(y1,y2,…,yn),当xi 2.1 问题描述 某配送中心与该市的多个超市合作进行物流配送服务。据实际情况,各个超市点的日需求量是不确定的。配送中心每天根据各超市点的需求向其执行配送任务,因为城区不同时段不同的路况,以及天气情况的影响,配送过程中车辆的行驶时间也是不确定的。在各超市点对配送中心服务满意的前提下,考虑以上不确定因素的影响,车辆如何配送货物使行驶时间最短,是本文要解决的问题。 在配送过程中,为了不影响正常经营,所有超市点设定了接受配送的时间窗口,即规定了配送车辆的到达时间范围。已知配送中心配送的是可混装的物资,并且运载的货物量都能满足客户需求。这里,配送中心有足够的运力可供调配车辆, 每辆车的一次载重量不能超过其额定载重量,而且每个超市点只能由一辆车服务,每辆车最多使用一次,车辆行驶的每条路线的起点和终点都在配送中心。 在本文中,车辆的行驶时间和各超市点的日需求量是不确定的变量,并且假设它们都是独立的。在建模之前,先介绍参数: i=0为配送中心;i=1,2,…,n为超市点;k=1,2,…,m为车辆;ξi为超市点的日需求量,i=1,2,…,n;γi为ξi的不确定分布,i=1,2,…,n;ηij为车辆从超市点i到超市点j的行驶时间,i,j=0,1,2,…,n;Φij为ηij的不确定分布,i,j=0,1,2,…,n;Ck为车辆的载重量,与车型相关,k=1,2,…,m;[ai,bi]为超市i接受配送的时间窗口,i=1,2,…,n。 本文描述的是带时间窗口的超市物流配送问题, 这里的配送过程用决策向量x,y,t来表示:x=(x1,x2,…,xn),整数向量,代表n个超市点,其中1≤xi≤n,且当i≠j时,xi≠xj,这里i,j=1,2,…,n。 y=(y1,y2,…,ym-1),整数向量,代表车辆的使用情况,且y0≡0≤y1≤y2≤…≤ym-1≤n≡ym。对于每个k(1≤k≤m),若yk=yk-1,则车辆k不使用,若yk>yk-1,则车辆k使用。 t=(t1,t2,…,tk,…,tm),tk代表车辆k从配送中心出发的时间。 若车辆k被使用,在时刻tk从配送中心出发,其配送路线为:0→xyk-1+1→xyk-1+2→…→xyk→0。 以上决策变量x,y,t可确保: (1)每辆车最多使用一次。 (2)所有路线的起点与终点都是配送中心。 (3)每个超市点有且仅有一辆车服务。 (4)配送路线经过每个超市点, 且不重复。 用fi(x,y,t,η)表示车辆到达超市点i时的到达时间函数,其中i=1,2,…,n。在这里不妨假设当fi(x,y,t,η)在时间窗口的开始时刻ai之后时,车辆可立即卸货; 当fi(x,y,t,η)在时间窗口的开始时刻ai之前时,车辆要等到时刻ai才能卸货。本文中车辆在超市点的卸货时间忽略不计。 对车辆k,1≤k≤m,当车辆k被使用,即yk>yk-1时,有 fxyk-1+1(x,y,t,η)=tk+η0xyk-1+1 (1) 此时到达超市点xyk-1+1的时间fxyk-1+1(x,y,t,η)是不确定变量,其逆分布为 (2) 且 fxyk-1+j(x,y,t,η)=fxyk-1+j-1(x,y,t,η)∨axyk-1+j-1+ηxyk-1+j-1xyk-1+j (3) (4) 其中2≤j≤yk-yk-1。这个递推过程能够推出车辆k到达所有超市点时间的逆分布。 2.2 模型的建立 我们希望每个超市点i(1≤i≤n)都在接受配送的时间窗口[ai,bi]内被服务(即车辆在时刻bi前到达超市点i处)的置信水平为α, 于是有以下机会约束: M{fi(x,y,t,η)≤bi}≥α (5) 由于居民在城区的分布密度不同, 各超市点每天货物的需求量是不确定的。这里各种车辆的载重量为Ck,k=1,2,…,m, 则车辆所到达超市点的货物需求量之和要小于车辆载重量。给定一个置信水平β, 有下面的机会约束: (6) 令Tk(x,y,η)为车辆k在配送过程中的总行驶时间, 则 (7) 现建立超市物流配送的不确定规划模型如下 (8) 其中α和β是给定的置信水平。 3.1 模型的转化 上节给出了带时间窗口的超市物流配送不确定规划模型,其中含有很多不确定变量。如何求解此类不确定规划模型? 一般情况下,我们希望将不确定规划模型转化为确定形式,从而对模型进行简化。接下来,我们主要讨论模型的转化问题。 定理5 假设ξi和ηij是独立的不确定变量, 且它们的不确定分布分别为Υi和Φij, 则模型(8)可以转化为 (9) (10) 证明 根据定理2,不确定变量期望值算子的线性性质(10)显然成立。 利用定义1,不确定变量的逆分布, 约束条件(5)等价于 (11) 且约束条件(6)等价于 (12) 定理得证。 3.2 算法 99算法是Liu[13]提出来的, 用来计算不确定变量中单调函数的不确定分布。 我们用表1来表示不确定变量ζi。 表1 不确定变量ζi的分布 步骤1 设E=0,j=1。 步骤3 若j<99, 令j←j+1,回到步骤2。 步骤4 得到E即为E[ζi]估计值。 由于模型(9)比较复杂, 用传统的方法不能解决。下面给出求模型近似最优解的一个算法。 算法 步骤1 输入初始参数值n,m,Ck及目标函数值S(此处S是一个足够大的正数),令超市物流配送计划x=0,y=0且t=0。 … … 否则, 返回1; 步骤4 若S′ 步骤5 重复第二步到第四步操作, 如此重复循环检验直到满足终止条件。 步骤6 输出的最终结果(x;y;t)即为最优解, 且S是最优目标函数值。 作为模型的实际应用,我们给出一个数值算例。黄冈市某配送中心向7个超市点提供配送服务,用于配送的3辆车的载重量分别为C1=10,C2=14,C3=16,单位是吨。据实际情况,7个超市点的日需求量是不确定的,车辆在配送路途中,受车流量和红绿灯等影响,行驶时间也是不确定的。假设超市的日需求量服从表2所示的之字形不确定分布ξi~Zi(a,b,c),i=1,2,…,7 。 表2 超市的日需求量ξi的之字形不确定分布Zi(a,b,c) 车辆的行驶时间服从正态不确定分布(单位:小时) Tij~N(|i-j|,1),i,j=0,1,2,…,7 其中当i=j=0时,Tij=0。 又已知7个超市点接受配送的时间窗口如表3所示 表3 各超市点接受配送的时间窗口 而且车辆在超市点接受配送的时间窗口内到达的置信水平为0.9, 车辆所到达超市点的货物需求量之和小于车辆载重量的置信水平为0.95。 根据以上给出的数值, 模型(9)即为 (13) (14) 车辆1 配送中心→2→3→配送中心,出发时间6∶22; 车辆2 配送中心→1→配送中心, 出发时间5∶17; 车辆3 配送中心→4→5→6→7→配送中心, 出发时间7∶27,此时车辆最短行驶时间T=22。 本文基于不确定理论, 研究了不确定环境下带时间窗口的超市物流配送问题。在配送过程中, 超市点的日需求量和配送车辆的行驶时间是不确定变量, 为了最小化配送车辆的行驶时间, 建立了不确定规划模型。又用不确定理论的基础知识对该模型进行转化, 再给出了算法来解所建立的数学模型。最后用一个数值算例说明了模型的实际应用。文章只是研究了单个配送中心向各超市点运送货物的例子, 对于多个配送中心向超市点运送货物的问题建模是今后值得深入思考的问题。 [1] 贺国先,刘凯.优化物流中心配送方案的遗传算法[J].系统工程理论与实践,2003,(4):76- 81. [2] 李延晖,刘向,马士华.基于时间约束的多源多品种随机配送系统模型[J].科技管理创新,2006,(6):69-71. [3] 王绍仁,马祖军.航空紧急配送中的随机LRP模型及算法[J].计算机应用,2010,30(12):3207-3210. [4] 张乐诚,杨信丰.随机时间约束的城市物流配送车辆路径问题研究[J].物流技术,2005,(9):68-70. [5] Liu B. Uncertainty theory[M]. 2nd ed. Berlin: Springer-Verlag, 2007. [6] Liu B. Theory and practice of uncertain programming[M]. 2nd ed. Berlin: Springer-Verlag, 2009. [7] Zhang B, Peng J. Uncertain programming model for Chinese postman problem with uncertain weights[J]. Industrial Engineering and Management Systems, 2012, 11(1): 18-25. [8] Gao Y. Uncertain models for single facility location problems on networks[J]. Applied Mathematical Modeling, 2012, 36(6): 2592-2599. [9] Ding S. A new uncertain programming model for grain supply chain design[J]. Information: An International Interdisciplinary Journal, 2013, 16(2): 1069-1076. [10] Jiang G. An uncertain programming model of chance constrains for empty container allocation[J]. Information: An International Interdisciplinary Journal, 2013, 16(2): 1119-1124. [11] Rong L. Two new uncertainty programming models of inventory with uncertain costs[J]. Journal of Information and Computational Science, 2011, 8(2): 280-288. [12] Zhang B, Peng J. Uncertain programming model for uncertain optimal assignment problem[J]. Applied Mathematical Modeling, 2013, 37(9): 6458- 6468. [13] Liu B. Uncertainty theory: A branch of mathematics for modeling human uncertainty[M]. 2nd ed. Berlin: Springer-Verlag, 2010. Uncertain Programming Model for Supermarket Logistics Distribution with Time Windows WU Pan-feng, LIU Hui-qing, PENG Jin (1.SchoolofMathematicsandStatistics,HubeiUniversity,Wuhan430062,China; 2.InstituteofUncertainSystems,HuanggangNormalUniversity,Huanggang438000,China) This paper deals with the supermarket logistics distribution problem with time windows in an uncertain environment. The daily demands of supermarkets and travel times of vehicles are treated as uncertain variables. In order to minimize the total travel time of all the vehicles, an uncertain chance constrained programming model is constructed. Then the proposed model is converted into a crisp equivalent model by operational law of uncertain variable. Moreover, an algorithm for solving the model is designed. Finally, a numerical example is presented to illustrate the modeling idea. logistics distribution; time windows; uncertain variables; chance constrained 2014- 02-26 教育部人文社会科学基金项目(13YJA630065);湖北省自然科学基金重点项目(2012FFA0 65);湖北省教育厅科技创新团队项目(T201110) 吴攀峰(1988-),女,湖北襄阳人,硕士研究生,研究方向为不确定理论及其应用;刘慧清(1968-),女,湖北大悟人,博士,教授,研究方向为图论与组合优化;彭锦(1961-),男,湖北麻城人,博士,教授,研究方向为不确定理论及其应用。 O221.2 A 1007-3221(2015)06- 0058- 07 10.12005/orms.2015.0196
2 问题描述与模型的建立
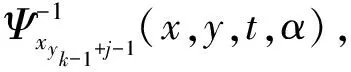
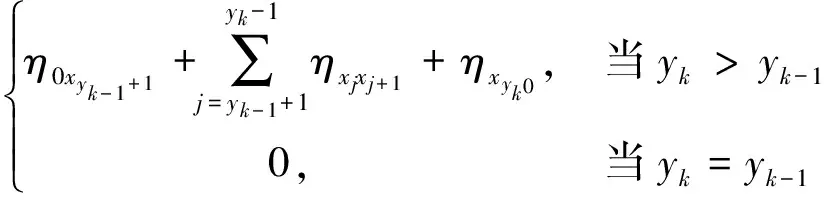

3 模型的转化与算法

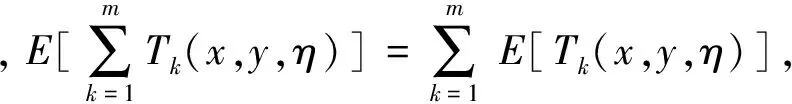
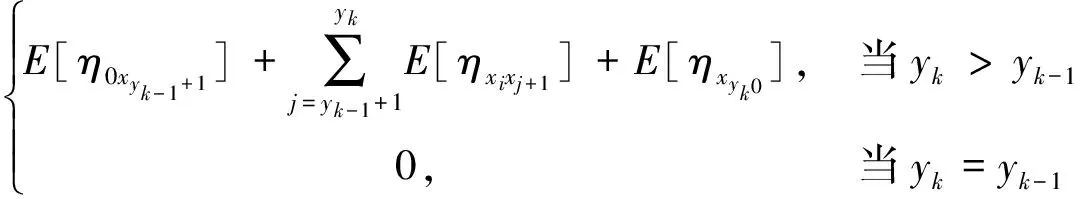



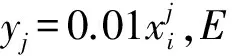
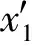
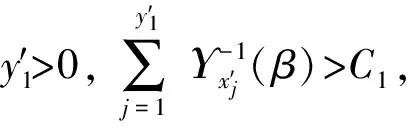

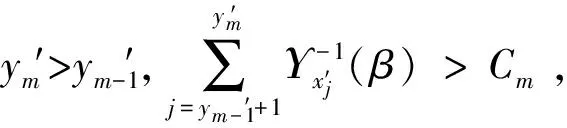
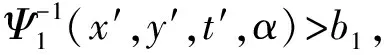


4 数值算例



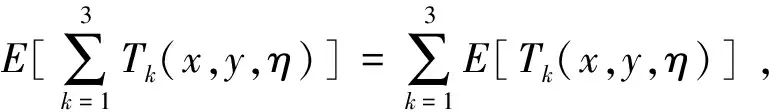
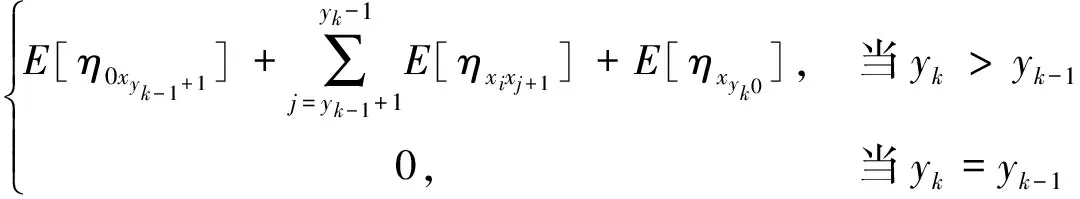
5 结束语

