基于灰色聚类的高校教辅人员综合评价

李志亮，罗芳，阮群生

(宁德师范学院计算机系，福建宁德352100)

基于灰色聚类的高校教辅人员综合评价

李志亮，罗芳，阮群生

(宁德师范学院计算机系，福建宁德352100)

灰色聚类是一种利用小样本数据进行统计分析的模糊优选方法，利用灰色聚类可以很好的对小样本数据的对象进行灰度划分.本文利用灰色聚类分析法进行教辅人员工作评价，构建了教辅人员工作评价模型，利用灰色聚类模型对教辅人员工作情况进行分析、计算和评价，得出了教辅人员工作灰类划分结果.通过具体实例分析说明，该模型快捷、简便，能够有效避免对教辅人员工作评价的盲目性，为教辅人员的选拔、聘任和评价提供量化依据.

灰色聚类;聚类系数;白化权函数;工作评价

近几年，随着大批的大专院校升为本科院校，高校的教育质量问题显得十分严峻.教辅人员整合教育资源配合教师完成教学工作，是一个重要的教育幕后工作者.许多高校十分重视教师队伍的建设却忽视了教辅人员素质的提升.许多教辅人员服务意识不高，工作效率低下，难以的配合教师较好的完成日常教学工作.为此建立一个适合的高校教辅人员评价模型，合理评价教辅人员的工作，充分调动广大教辅人员的工作积极性，成了众多高校迫在眉睫的问题.

灰色系统理论主要用于解决含未知因素的问题［1］，灰色聚类法作为其重要组成部分被广泛用于水、大气、土壤环境质量评价［2－4］，证券投资分析［5］，区域经济实力评价［6］等.近几年，许多学者将灰色聚类法应用于高校教学方面［7－8］，通过灰色聚类法通过构造白化权函数，计算聚类对象的差异性来分析和建立评价模型.基于中心点三角白化权函数能够方便、快捷的划分每个对象所属的各灰类，但存在不清晰的边界划分［9－10］，1993年刘思峰［11－12］首先提出了端点三角白化权函数，2011年对传统白化权函数进一步改进，提出中心点三角白化权函数.本文采用灰色聚类分析中改进白化权函数建立高校教辅人员综合评价模型，并结合某高校教辅人员的评价实例来说明灰色聚类的过程，为教辅人员的选拔、聘任和评价提供量化依据.

1 灰色聚类模型的构建

设待考核的人员有m个，考核人员的评估指标有n个，对考核人员评估结果有s个，即有s个灰类.对象i关于评估指标j的取值为xij，其中i∈［1，m］，j∈［1，n］，对象i划分为第k类，其中k∈［1，s］.采用灰色聚类方法对xij的取值进行分析、处理，得到考核人员i的评估结果，即评价考核对象i所属的灰色聚类k.

采用改进的三角白化权函数的灰色聚类具体步骤如下:

(1)确定灰类数及取值范围

按照建立评估模型的要求，划分灰类数s个.同时将评估指标的取值范围按照实际需求划分为s个区间，它们分别为

其中aj的值可以根据现实测量或实际数据的取值获得.

(2)确定灰类的转折点和中心点

按照步骤(1)中的灰类数，逐步确定灰类1的转折点，灰类s的转折点和灰类k的中心点，并分别记

(3)构建改进的白化权函数

构造的白化权函数示意图如图1、图2、图3所示.

图1 下限测度白化权函数图

图2 中心点三角白化权函数图

图3 上限测度白化权函数图

(4)确定灰色聚类指标权重

灰色聚类的权重是对同一灰类划分的权值的衡量指标，一般采用ωj来表示第j个指标的权重.指标权重分为主观权重和客观权重，主观权重可采用层次分析法［13］计算;客观权重可采用离差最大化法［14］计算;也可以计算主观、客观组合权重系数，通过组合赋权法［15］有效的融合主、客观权重，进而得到灰色聚类的指标权重;当然也可以根据实际数值得到指标权重的值.

(5)计算灰色聚类系数

(6)确定灰色聚类

2 教辅人员工作评价实例

2.1 建立灰色聚类评价矩阵

本文对某高校5名教辅工作人员进行灰色聚类的实证评价研究，将考核对象的思想品德、业务能力、工作态度、工作效果、廉洁程度和工作量作为灰色聚类的评价指标，量化分值记为xij，其中i为考核对象的编号，i∈［1，5］;j为考核指标的编号，j∈［1，6］，i，j均为整数.将考核对象的评价分为优秀、良好、合格和不合格四种.5名考核对象的评价指标评分值如表1所示:

表1 某高校教辅工作人员评分值

由表1可得到灰色聚类评价矩阵Ma如下:

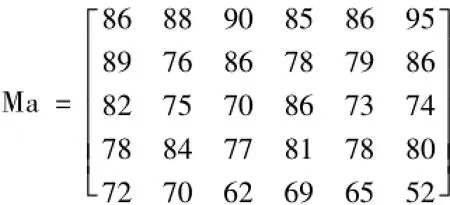
2.2 三角白化权函数的建立

2.2.1 确定灰类数及取值范围

灰类数记为m，结合某高校实际情况，将考核对象的评价分为优秀、良好、合格和不合格四种，所以m=4.其中不合格的取值范围为［50，70］，划分为灰类1;合格的取值范围为［60，80)，划分为灰类2;良好的取值范围为［70，90］，划分为灰类3;优秀的取值范围为［80，100］，划分为灰类4.

2.2.2 确定灰类的转折点和中心点

由表1可得到考核对象的相应指标的最低值和最高值，因此确定数值区间为［50，100］，其中灰类1即不合格灰类的转折点为60，灰类4即优秀灰类的转折点为90，灰类2和灰类3的中心点分别为70和80.

2.2.3 构建灰类的白化权函数

由公式1、公式2、公式3得到考核对象的白化权函数.

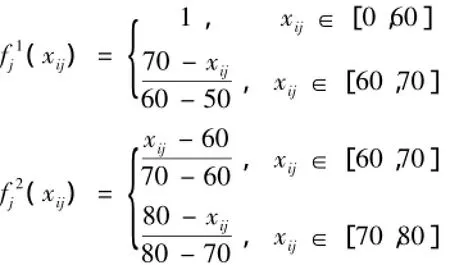
2.2.4 计算权重

根据某高校对教辅工作人员的思想品德、业务能力、工作态度、工作效果、廉洁程度和工作量6个考核指标中，每个评价指标的权值该高校取值如下:0.15，0.2，0.1，0.25，0.12，0.18.即ω1=0.15，ω2= 0.2，ω3=0.1，ω4=0.25，ω5=0.12，ω6=0.18.

2.2.5 计算灰色聚类系数

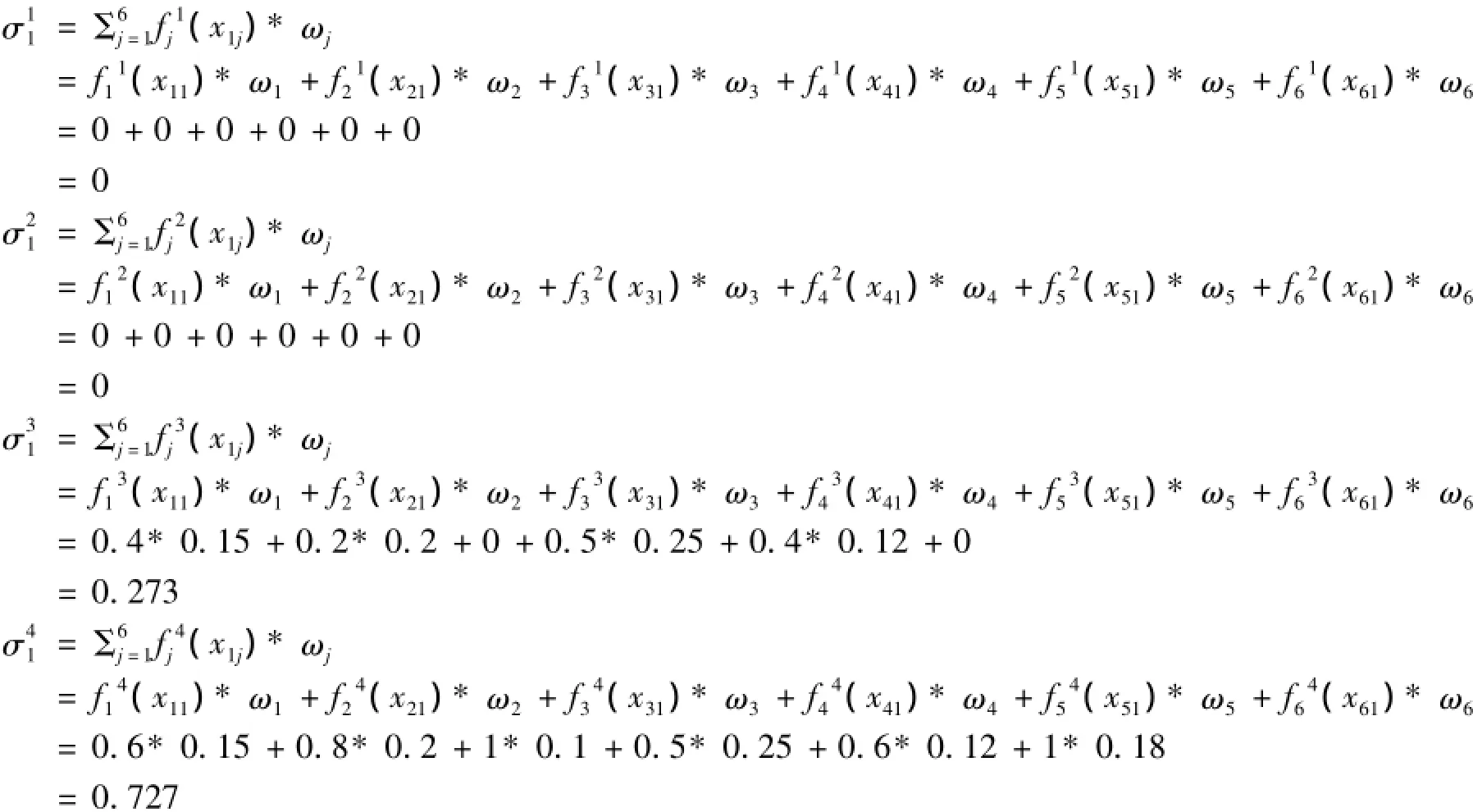
同理可以得到考核对象的其它灰色聚类系数，结果见表2.

表2 考核对象评估聚类系数表

2.2.6 确定灰色聚类

由表2可得到每个考核对象的评价的灰色聚类向量，5个考核对象的灰色聚类向量为

σ1=(0，0，0.273，0.727)，σ2=(0.0.25，0.555，0.303)，σ3=(0，0.492，0.578，0.03)，σ4=(0，0.084，0.811，0.105)，σ5=(0.745，0.255，0.03，0).

3 结束语

由于聚类分析具有很强的实用性，所以聚类分析受到了人们的重视并推广应用，其中灰色聚类分析是聚类分析中的新方法，近年来已经逐步发展和完善，所以灰色聚类分析也可以用到很多聚类的领域.灰色聚类分析中的白化权函数对于聚类结果的准确性和实用性具有重要的影响.因此本文构建了一种改进的灰色聚类评估方法，通过对中心点白化权函数的改进，很好的延伸灰色聚类指标的范围.将改进的灰色聚类模型首次应用到高校教辅人员的工作评价上，验证了灰色聚类模型的实用性，为教辅人员的选拔、聘任和评价提供量化的依据.

［1］邓聚龙.灰理论基础［M］.武汉:华中科技大学出版社，2002.

［2］Smeltzer E，Shambaugh A，Stangel P.Environmental change in lake champlain revealed by longuterm monitoring［J］.Journal of Great Lakes Research，2012，38(1):6－18.

［3］赵丹，易英欣.基于灰色聚类评价模型的研究生招生质量研究［J］.黑龙江高教研究，2014(11):46－49.

［4］张丽，李广杰，周志广，汪茜.基于灰色聚类的区域地质灾害危险性区域评价［J］.自然灾害学报，2009，18(1):164－168.

［5］李星.模糊聚类与灰色聚类在我国证券投资中的应用［D］.株洲:湖南工业大学，2012.

［6］孙晓利，董春，李青元.灰色聚类法在区域经济发展水平综合评价中的应用［J］.测绘科学，2008，33(6):160－162.

［7］于俊乐，许青.高校教学管理质量评价信息综合处理方法研究［J］.天津师范大学学报，2007，27(2):73－75.

［8］赵丹，易英欣.基于灰色聚类评价模型的研究生招生质量研究［J］.黑龙江高教研究，2014(11):46－49

［9］刘思峰，谢乃明.灰色系统理论及其应用［M］.北京:科学出版社，2013.

［10］Liu S F，Xu Bin，Jeffrey Forrest，et al.On uniform effect measure functions and a weighted multi－attribute grey target decision model［J］.J of Grey System，2013，25(1):1－12.

［11］刘思峰，朱永达.区域评估指标与三角隶属度评估模型［J］.农业工程学报，1993，9(2):8－13.

［12］刘思峰，谢乃明.基于改进三角函数白化权函数的灰评估新方法［J］.系统工程学报，2011，26(2):244－249.

［13］马农乐，赵中极.基于层次分析法及其改进对确定权重系数的分析［J］.水利科技与经济，2006，12(11):732－733.

［14］董一哲，党耀国.基于离差最大化法的灰色聚类方法［J］.系统工程理论与实践，2009，29(9):141－146.

［15］陈伟，夏建华.综合主、客观权重信息的最优组合赋权方法［J］.数学的实践与认识，2007，37(1):17－21.

Evaluation on Teaching Staff in Universities Based on Grey Clustering

LI Zhi－liang，LUO Fang，RUAN Qun－sheng
(Department of Computer Science，Ningde Normal University，Ningde，352100，China)

The grey clustering is the preferred method using small sample data for statistical analysis，the use of grey clustering can be a good target for small samples of grey division.In this paper，the grey clustering analysis method is used to evaluate the teaching staff，build an evaluation model，using grey clustering model to analyze，calculate and evaluate the work of the teaching staff，get the grey division results.Through concrete examples analysis shows that the model is fast and easy，can effectively avoid the evaluation blindness of teaching staff.It provides a quantitative basis for the selection，appointment and evaluation of teaching staff.

grey clustering;clustering coefficient;whitenization weight function;job evaluation

G647

A

1672－2590(2015)06－0038－05

2015－09－28

福建省自然科学基金项目(2011J01357);宁德师范学院服务海西资助项目(2012H405);福建省大学生创新创业训练计划项目(201410398059)

李志亮(1981－)，男，山东禹城人，宁德师范学院计算机系讲师.