激光跟踪仪精密跟踪转台轴系优化设计
林心龙,周维虎,劳达宝
(1.中国科学院大学,北京 100190;2.中国科学院光电研究院,北京 100094)
激光跟踪仪精密跟踪转台轴系优化设计
林心龙1,2,周维虎1,劳达宝1
(1.中国科学院大学,北京 100190;2.中国科学院光电研究院,北京 100094)
精密跟踪转台是高精度飞秒激光跟踪仪的关键单元,其精度直接影响激光跟踪测量系统的总体精度,而跟踪转台的精度主要由轴系精度决定,因此跟踪转台的轴系结构设计以及对其轴系进行性能分析非常重要。文中首先对精密跟踪转台进行结构设计与建模,利用SAMCEF of rotor软件对二维转台2个轴系进行了仿真分析。根据激光跟踪仪性能要求与仿真结果对轴系结构进行分析与优化。最后通过搭建的二维转台验证了所设计轴系的可行性,能够满足激光跟踪仪跟踪转台高精度、高灵敏度和低跳动的要求。
激光跟踪仪;跟踪转台;轴系;有限元分析
0 引言
新型飞秒激光跟踪仪具有测量功能多、测量精度高、测量速度快、量程大、可现场测量等特点,是大型科学工程和大型高端装备制造中急需的测量装备。二维转台是高精度飞秒激光跟踪仪的主要组成部分,作为目标跟踪的执行机构,其性能直接影响激光跟踪测量系统的跟踪性能;它也是跟踪仪测角装置的承载机构,直接影响仪器的测角精度;同时也是跟踪仪测距光路的辅助部件,影响测距性能。因此,精密跟踪转台是实现高性能飞秒激光跟踪仪的关键因素及基础。
目前国内外学者对转台精度的研究主要集中在消除指向误差[1-2]、测角系统误差[3]、垂直度误差[4]、轴线不相交[5]等方面,或者利用多体动力学的方法对转台进行空间综合误差建模与分析[6-7]。本文主要针对跟踪转台主要性能指标中,对轴系测角精度具有重要影响的轴系振动特性进行仿真分析和研究,并根据仿真结果对轴系结构进行优化。最后通过搭建的二维实验转台验证了所设计轴系的可行性,测角精度经过修正后可达到0.5″,正弦引导精度可达2.0″,满足了飞秒激光跟踪仪的高性能要求。
1 轴系设计
激光跟踪仪精密跟踪转台由方位轴系和俯仰轴系构成,其中方位轴系主要部件包括外壳、轴套、角接触轴承组、光栅编码器、读数头、力矩电机、垂直通轴等。该轴系采取轴端固定支承轴套的方式模拟经典半运动式轴系[8],以便于调整装拆。因垂直通轴主要承受轴向力,故采用配对的角接触球轴承来抵消轴向力,增强承载刚度,减小轴向跳动误差,同时方位轴系需要方便安装调试,采用角接触球轴承可以简化结构设计,便于预紧和消除间隙。轴和轴套选用GCr15轴承钢材料,通过精密加工保证轴与轴套椭圆度及其滑动配合间隙,并添加仪表油保证其灵活转动。方位轴系三维模型如图1所示,对应的二维剖面图如图2所示。

(a) 完整图

(b) 不含外壳和读数头支撑架

图2 方位轴系剖面图
俯仰轴系主要部件包括外壳、轴套、角接触轴承组、深沟球轴承、光栅编码器、读数头、力矩电机、俯仰通轴、跟踪转镜、电子倾角传感器等。俯仰轴系并未采用传统的经纬仪左右轴独立的形式,而采用通轴形式,保证俯仰轴具有较好的同轴精度,轴和轴套材料均选用GCr15轴承钢,以保证温度变化对轴系精度的影响[9]。轴系采用双联角接触球轴承作为主支撑,同时设置了一个深沟球轴承作为辅助端,双联角接触球轴承承受的负荷大,寿命长,定位精度高,适用于对转速、刚度等都有很高要求的设备[10],保证俯仰轴不会轴向窜动,减小轴向跳动误差。为了保证轴系精度,双联轴承需加预载过盈,使轴承稍带负的运转游隙。深沟球轴承用于防止俯仰轴因温度变化引起的伸缩对轴系转动的影响,减小轴端跳动误差。俯仰轴系三维建模如图3所示,对应的二维剖面图如图4所示。

(a) 完整图

(b) 不含外壳和读数头支撑架

图4 俯仰轴系剖面图
俯仰壳体是整个水平轴系的支撑骨架,大多数的机械机构都含纳其中。所以俯仰壳体的强度、刚度、质量、内部结构、外型尺寸等是直接影响轴系设计的基础因素。内部尝试将双U型架与壳体做成一体,虽然增加了壳体浇铸加工难度,但减少了联接件数量,增加了定位精度。俯仰壳体采用铸铝结构,主要材质为ZL201,ZL201具有密度相对较低,力学性能较好的优点[11],通过在薄弱环节加加强筋,以保证在刚度合格的前提下使整个俯仰轴系质量最小。
2 转子有限元分析原理
对于主轴系统,过去进行的性能分析主要采用简化计算方法,这类方法计算量小,但需要简化合理,否则计算结果与实际情况相差比较大,不能很好地满足设计要求。近年来由于科学技术的发展,尤其是计算机运算性能的提升,可采用有限元法进行较精确的计算[12-13]。
根据轴系转子系统的结构特点,将球轴承转子系统的振动作为梁的横向弯曲振动处理。利用达朗贝尔原理,考虑惯性力与阻尼的影响可以方便地建立主轴的运动微分方程,如式(1)所示:
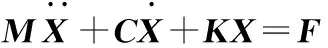
(1)
式中:M为单元矩阵;K为单元刚度矩阵;C为阻尼矩阵;X为系统的总体位移列向量;F为系统的总体载荷列向量。
球轴承转子系统的阻尼主要来自轴承内部的弹流润滑油膜。滚珠与套圈沟道的弹流油膜很薄,尤其是保持架含油润滑的微机械陀螺马达轴承,另外阻尼也不容易从理论上求得,具有不确定性,属于概率分布与趋势规律都未知的乏信息系统,所以系统的阻尼可以忽略,故转子的运动微分方程和自由振动方程分别简化如式(2)、式(3)所示:
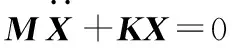
(2)
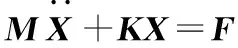
(3)
求解方程(2)的特征值和特征向量,即可得到系统的固有频率和结构振型,求解方程(3)可以得到系统的振动响应等其他转子动力学特性。
3 仿真分析
本文采用SAMCEF for Rotor仿真软件对方位轴系和俯仰轴系进行仿真分析。SAMCEF for Rotor是一款基于有限元方法,专门致力于旋转机械分析的专业仿真软件。该软件主要基于上节所介绍的转子有限元分析原理进行仿真计算。
因激光跟踪仪主要工作于低速状态下,两个轴系的工作转速远低于通过仿真所得的各阶临界转速,可见其在正常工作环境下不会因共振而产生较大振幅,故不需进行过多动力学分析。本文主要研究两个轴系在工作转速下,轴颈、轴承位置及不平衡质量对轴系振幅与振型的影响,并根据仿真结果优化轴系的结构设计。
3.1 方位轴系
3.1.1 不同轴径下的轴系跳动振幅变化
首先分析方位轴系在不同轴径下的跳动振幅变化。由于方位轴轴端要分别固定光栅尺和连接法兰,需要做螺纹孔,且其通孔直径为20 mm,故限制了方位轴的轴端最小轴径,轴端最小轴径取设计值34 mm,此时轴系的工作振型图如图5所示。由图5可知,当轴端轴径取最小时,轴系最大变形量在轴端处,为0.16 μm,满足精度要求。
通过改变轴端轴径值,其他轴段处直径相应等量增加,得到轴系跳动振幅变化如表1所示,由于轴系的最大变形量在上轴端,故表1中表达的为轴端处的最大变形量。

图5 方位轴系工作振型图(轴径最小时)
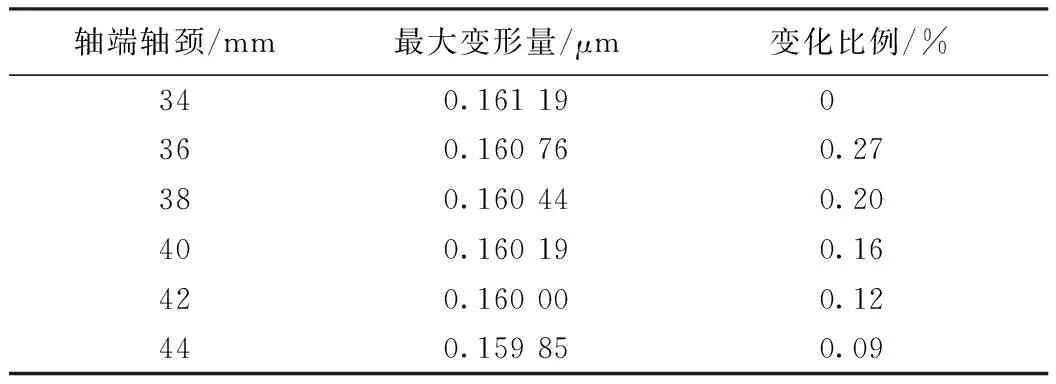
表1 不同轴径下的轴系跳动振幅
如表1所示,轴端变形量随轴端轴径的增加变化较小,且变化比例呈下降趋势。考虑到轴径增大将会造成整个仪器整体尺寸的增大,影响仪器的成本和工作性能,同时为了与轴承标准件相配合,故综合考虑最终选择垂直轴系轴端轴径为34 mm,其他轴段轴径相应变化。方位轴经最终优化后各轴段轴径如图6所示。

图6 方位轴各轴径尺寸图(优化后)
3.1.2 不同轴承位置时的轴系跳动振幅变化
轴承所在位置及轴承之间距离的变化均会直接影响轴系在正常转速范围内的跳动振幅变化,故通过分析轴承在不同位置时的轴系跳动振幅变化来选取轴承之间的最优位置与距离。现以方位轴下端轴承距离轴下端面的距离为基准距离,因为方位轴下端与方位电机相连,故由于结构原因下端轴承距离下端面的最小距离为29 mm,同时由于方位轴上端与连接法兰连接,故由于结构原因上端轴承距离下端面的最大距离为85 mm。取方位轴向上为正方向,通过改变下端轴承的位置和两轴承的间距分析轴系轴承的最优位置。仿真数据见表2。
由表2分析可得,下端轴承距离方位轴下端面距离越大,方位轴系跳动振幅越小;两个轴承之间的间距越大,方位轴系跳动振幅越小。由于方位轴主要承受轴向载荷,轴承间距的增大可以有效增大轴系的刚度,减小轴向变形。故综合考虑,最终选定下端轴承距离下端面的距离为29 mm,轴承间距为46 mm。图7为该轴承位置下的方位轴系振型图。

表2 不同轴承位置下的轴系跳动振幅
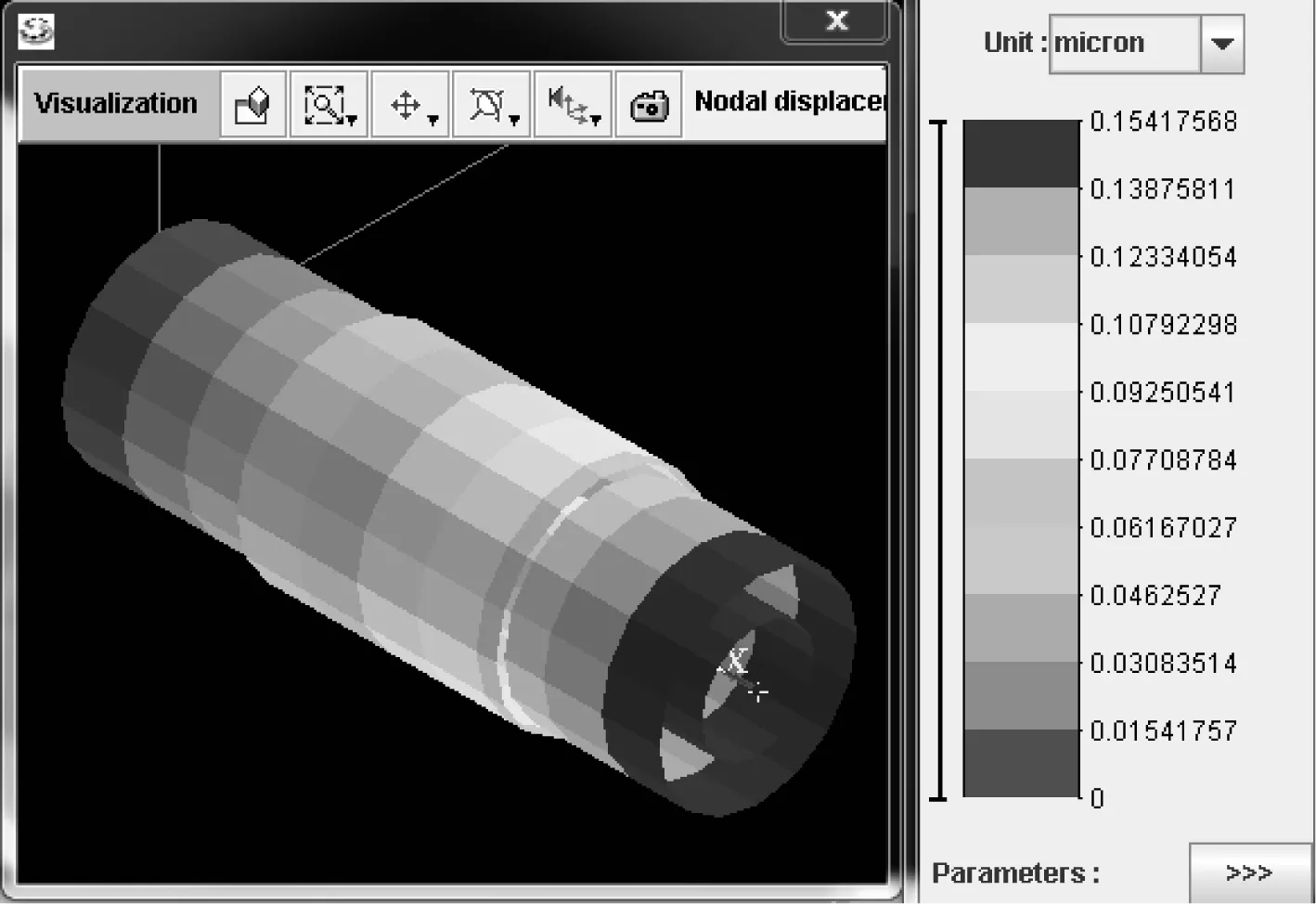
图7 方位轴系工作振型图(选定轴承位置下)
3.1.3 不同不平衡量下的轴系跳动振幅变化
动平衡是影响轴系设计的一个很重要的因素,会影响轴系的刚度、寿命以及回转精度等参数。在方位轴系中,产生不平衡量的主要是俯仰机构产生的负载,由于俯仰机构结构上不对称,故其重心并不在方位轴系的轴线上,故产生了不平衡量。在仿真中,主要用不平衡质量的偏移量来模拟由于俯仰结构不对称导致的不平衡量。通过比较不同偏移量下方位轴系跳动振幅的变化,最终计算出轴系在正常转速范围内满足精度要求情况下,动平衡所要达到的要求。具体仿真数据见表3。

表3 不同不平衡量下的轴系跳动振幅
由表3分析可得,方位轴系的跳动振幅与不平衡质量的偏移量呈比例增加,若要求轴系跳动振幅小于0.3 μm,即不平衡质量偏移量小于4 mm。配重公式如式(4)所示。
m1·L1=m2·L2
(4)
式中:m1为负载质量;L1为负载质心到转轴距离;m2为配平块质量;L2为配平块质心到转轴距离。
若进行配重设计时将配平块加于俯仰机构侧盖处(L2=85 mm),则要求俯仰机构侧盖处不平衡质量小于280 g。
为表述方便,现对俯仰机构建立坐标系如图8所示,取俯仰轴轴线为x轴,俯仰电机到光栅尺方向为x轴正方向,与方位轴轴线相交点为原点,其他两轴方向如图8所示。因为x轴上均为回转体,即沿z轴不存在明显不平衡质量,故仅分析x轴方向上的不平衡质量。用solidworks软件计算出俯仰机构主要部件质量与质心到转轴距离,如表4所示,其中x轴正半轴上质心到原点距离取正值,x轴负半轴上质心到原点距离取负值。

图8 俯仰机构坐标系示意图

表4 俯仰机构主要部件参数
由表4可知方位轴系的不平衡量产生在x轴正半轴,即若在俯仰机构左边盖处增加配重块消除不平衡量,由式(4)可得,配重块的质量为500 g,大于280 g,故必须要进行配重设计,进行不平衡量的消除。假设进行配重设计达到10 g数量级,则不平衡质量偏移回转轴心距离为0.14 mm。则经过最终优化后的方位轴系工作转速范围内的振型图如图9所示。

图9 方位轴系工作振型图(最终优化)
由图9可知,俯仰轴系在工作转速范围内的最大变形量发生在方位轴下轴端,振幅为0.011 μm,远远小于精度要求,故从理论上分析俯仰轴系结构设计满足精度要求。
3.2 俯仰轴系
俯仰轴系分析过程与垂直轴系相似,故省略分析过程,优化后的轴系结构尺寸及工作转速范围内的振型图分别如图10、图11所示。
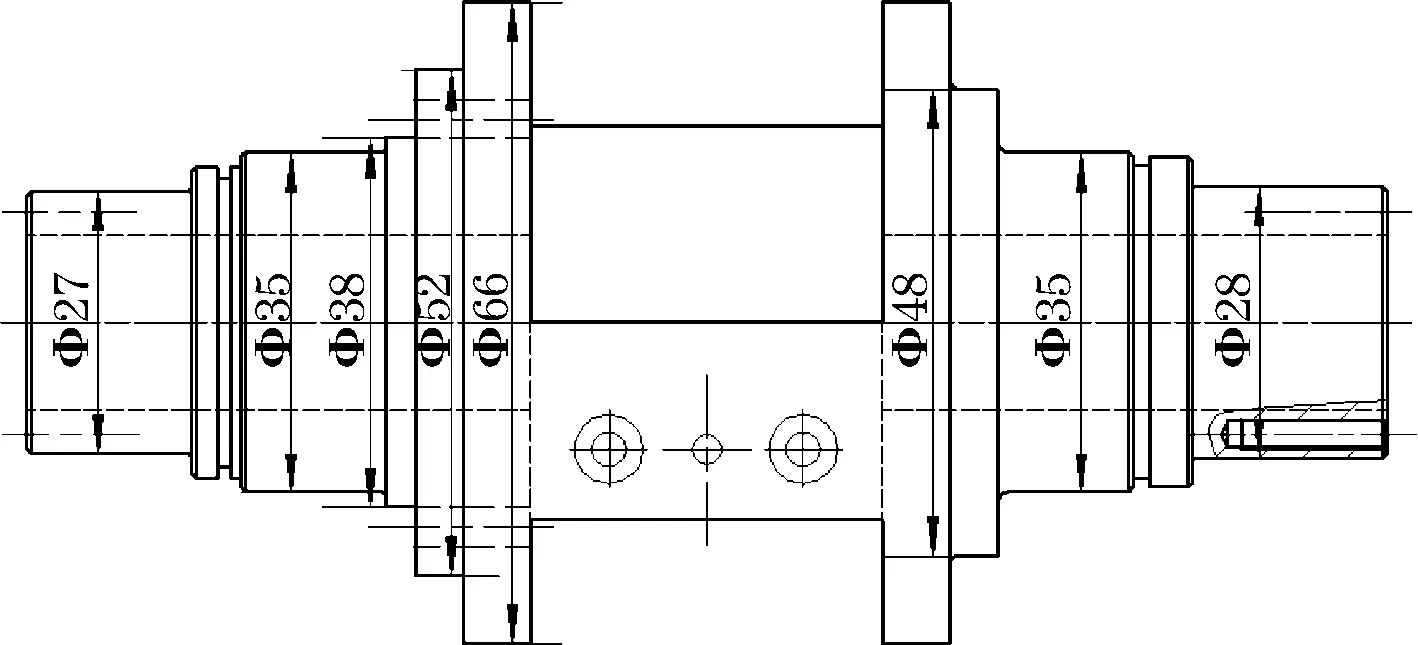
图10 优化后俯仰轴各轴径尺寸图
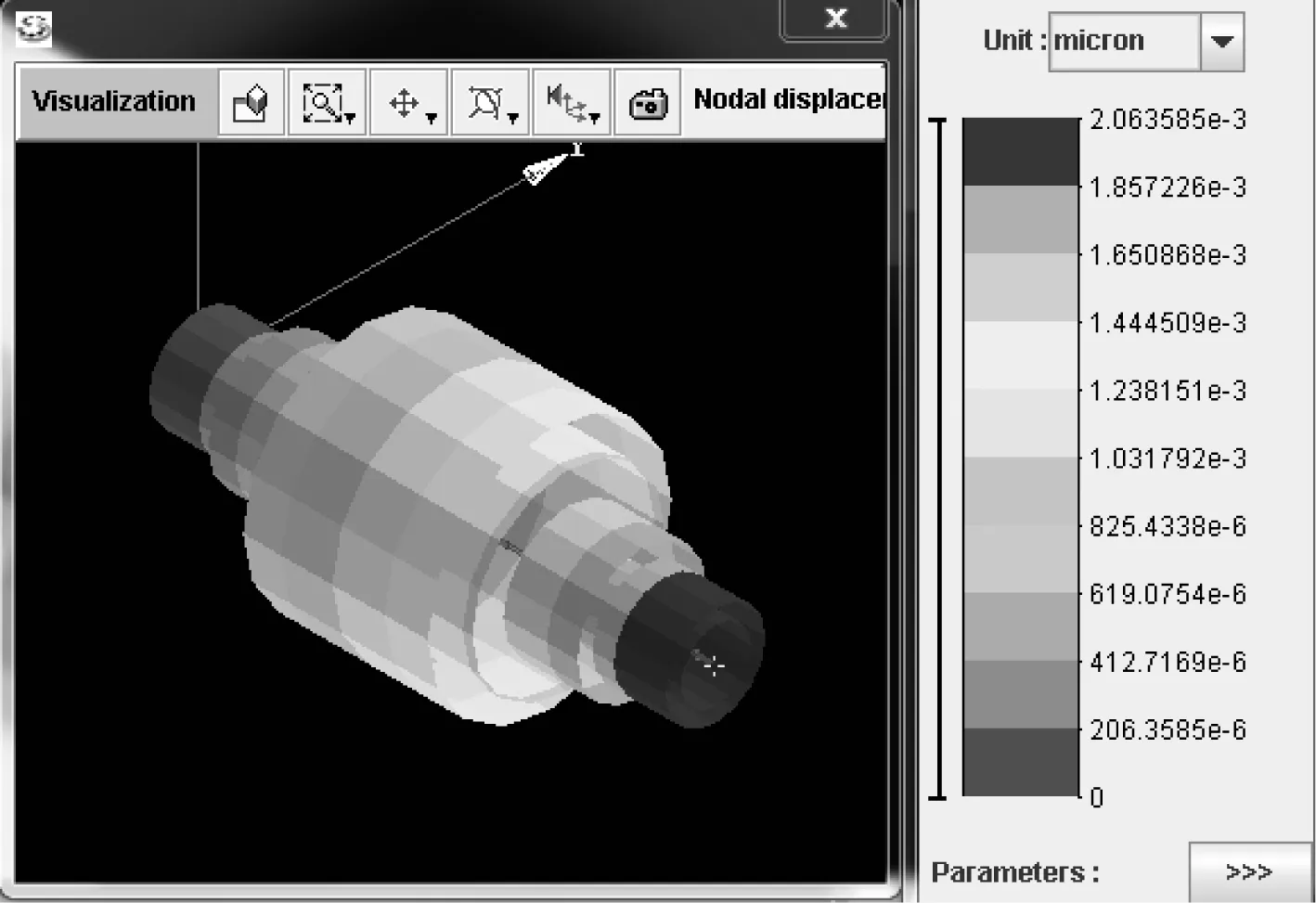
图11 优化后俯仰轴系工作振型图
由图11可知,俯仰轴系在工作转速范围内的最大变形量发生在光栅侧轴端,振幅为0.002 μm,远远小于精度要求,故从理论上分析俯仰轴系结构设计满足精度要求。
4 实验验证
经过初步验证,通过千分表测量轴系跳动为0.3″。为了进一步验证系统的精度,设计了2个试验:一是转台的测角精度测试;二是电机的正弦引导测试。
以方位轴系为例,因测角的重复性误差体现了系统的稳定性,即轴系精度的大小。故本文采用23面棱体和自准直仪在不同时间、重新装拆标定仪器的情况下对转台方位轴进行多次测量,获得多次测量误差曲线如图12所示。

图12 方位轴系测角误差
由图12可知,方位轴系测角的重复性误差为1.21″,具有较高的轴系精度和可靠性。
由于在实际测角误差标定试验中,不能精确地保证每次跟踪仪转动的位置一致性,即不能保证每个位置点跟踪仪测得角度值相等,同时为了减小随机误差的影响,所以取多次标定的测角误差平均值作为误差补偿源数据,如表5所示。

表5 23面棱体标定的误差平均值
由表5可知,该轴系未经补偿的测角精度为-1.21″~+1.12″,通过谐波补偿方法最终将测角精度由1.21″提高到0.51″。测角误差主要由安装误差和轴系跳动误差组成,其中安装误差一般为系统误差,而轴系跳动为随机误差。而本文基于仿真优化所设计的轴系结构有效地减少了轴系跳动等随机误差,从而使得测角装置能够经过软件补偿大大提高精度。
电机正弦引导测试是通过上位机模拟二维跟踪转台的运动轨迹,考察执行机构的响应速度、跟踪精度等综合性能,其引导精度主要由控制系统、电机性能及机械结构共同决定。通过与电机配合调试,方位正弦引导误差达到0.002°,均方误差为0.000 6°(2.16 ″)。方位正弦引导跟踪误差曲线如图13所示。
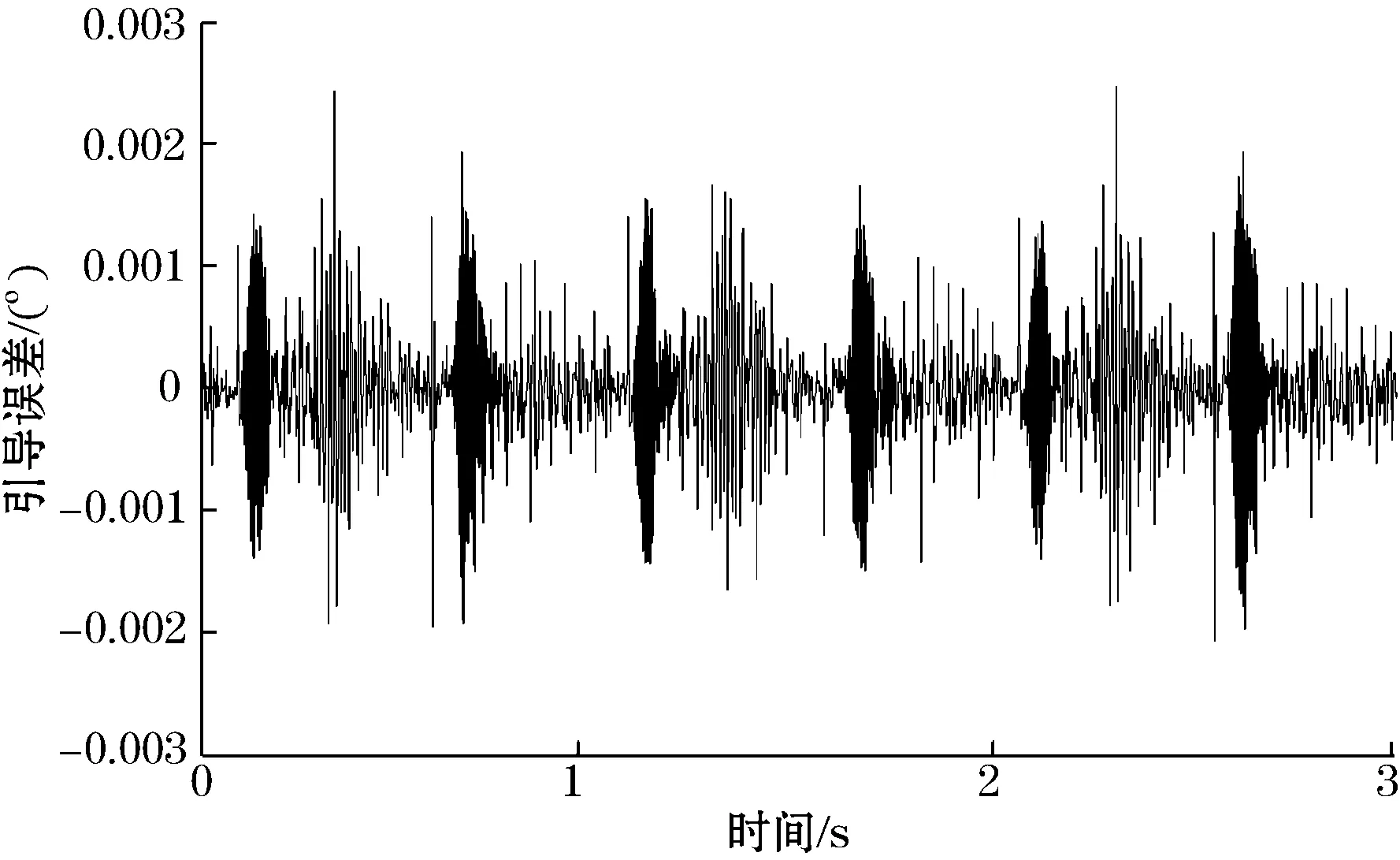
图13 方位正弦引导跟踪误差曲线
同样地,俯仰轴系的测角重复性误差为0.82″,未经补偿的测角精度为-1.17″~+4.50″,经过补偿后精度达到0.52″;正弦引导误差达到0.003°,均方误差为0.000 7°(2.52″)。由试验结果可知该二维转台符合低跳动、高精度的性能要求,与高性能电机配合可以实现高精度跟踪。
5 结束语
本文基于SAMCEF for rotors仿真软件分析了轴系负载不平衡质量、轴径、轴承位置等因素对转台方位和俯仰转动性能的影响,分析了不同参数情况下轴系旋转跳动的状态,初步确定了轴系参数选择对轴系性能影响的规律,并对轴系参数进行了优化。通过搭建二维试验转台,验证了所设计的二维轴系的可靠性,误差标定表明方位轴系测角精度可达到0.51″,正弦引导精度可达到2.16″,俯仰轴系测角精度可达到0.52″,正弦引导精度可达到2.52″,满足激光跟踪仪的高性能要求。
[1] 白雪峰,赵剡.单轴速率三轴位置惯性测试转台误差及传递分析.航天控制,2006(2) :26-29.
[2] 刘延斌,金光,何惠阳.轴仿真转台指向误差的建模研究.哈尔滨工业大学学报,2005 (5) :701-704.
[3] 邓辉宇,王欣利,苏宝库.三轴机械转台测角系统误差的非平稳性分析.中国机械工程,2002(12):2075-2097.
[4] 任顺清,陈希军,袭建军.三轴转台垂直度误差的测试与分离技术.计量技术,2002 (5 ):6-9.
[5] 王玉明,周兴义.测试转台轴线不正交对测量精度影响的分析.光学仪器,2008(1):11-14.
[6] 曲智勇,姚郁.仿真转台误差分析及误差建模.计算机仿真,2006 (3):301-304.
[7] 李岩,范大鹏.基于多体系统运动学理论的三轴转台装配误差建模分析.兵工学报,2007 (8) :981-987.
[8] 罗志刚,杜杰.成对双联角接触球轴承的性能与安装使用方法.哈尔滨轴承,2004,25(1):20-21.
[9] 王涛,唐杰,丛俊峰.基于标准轴承的经纬仪俯仰轴系设计.长春理工大学学报(自然科学版),2011,34(3):39-41.
[10] 王俊乾.高精度半运动式轴系工艺探讨.仪表技术与传感器,1979(1):17-18.
[11] 李有佳.铝合金铸造工艺及缺陷研究:[学位论文].武汉:华中科技大学,2009.
[12] 周传月.SAMCEF有限元分析与应用实例.北京:机械工业出版社,2009.
[13] 袁惠群.转子动力学基础.北京:冶金工业出版社,2013.
Optimized Design of Precision Tracking Turntable for Laser Tracker
LIN Xin-long1,2,ZHOU Wei-hu1,LAO Da-bao1
(1.University of Chinese Academy of Sciences,Beijing 100190,China ; 2.Academy of Opto-Electronics,Chinese Academy of Sciences,Beijing 100094,China)
The precision tracking turntable is the key unit in the high precision femtosecond laser tracker,and its accuracy directly influences the general accuracy of laser tracker system and depends on that of axis.Consequently,the design and analysis of axis structure in tracking turntable are important.In this paper,structure design and modeling of the precision tracking turntable were firstly designed,and then the software SAMCEF of rotor was applied to analyze the two axis of 2D turntable axis.Based on the property requirements and simulation results of laser tracker,the axis systems were analyzed and optimized.Finally,the 2D turntable was designed to validate the feasibility of the axis system,which can meet the requirements of high precision,high sensitivity and low jitter of laser tracker.
laser tracker;tracking turntable;shafting;FEA
国家重大科学仪器设备开发专项(2011YQ120022);中国科学院科研装备项目(090206A01Y);国家自然科学基金青年项目(61307095)
2014-03-31 收修改稿日期:2014-11-10
TH74
A
1002-1841(2015)04-0024-04
林心龙(1990—),硕士研究生,主要研究方向为精密机械设计与跟踪控制。E-mail:linxinlong12@mails.ucas.ac.cn 周维虎(1962—),研究员,博士生导师,主要研究领域为光电系统总体技术与集成测试,光电精密测量技术与系统,大尺寸测量技术与系统。E-mail:zhouweihu@aoe.ac.cn

