基于有限控制集模型预测控制的SAPF的研究

汪玉凤，周宏胭，刘存国，孟娜

(1．辽宁工程技术大学电气与控制工程学院，辽宁葫芦岛125105; 2．国网辽宁省电力有限公司阜新供电公司，辽宁阜新123000)

基于有限控制集模型预测控制的SAPF的研究

汪玉凤1，周宏胭1，刘存国2，孟娜1

(1．辽宁工程技术大学电气与控制工程学院，辽宁葫芦岛125105; 2．国网辽宁省电力有限公司阜新供电公司，辽宁阜新123000)

在并联型有源电力滤波器(SAPF)动态补偿电网谐波过程中，为了快速准确地跟踪并补偿谐波电流，对基于中点箝位三电平逆变器拓扑结构的SAPF进行了分析，提出一种有限控制集模型预测控制策略。首先通过重复预测器对负载电压和电流进行超前两拍的预测，在此基础上利用p-q理论计算出补偿电流超前两拍的参考值，然后根据参考电流值与补偿电流值之间的误差，运用有限控制集模型预测控制器进行反馈校正和滚动优化。仿真及实验结果表明:采用该控制策略的SAPF能有效降低电网电流的总谐波畸变率，具有很好的补偿效果和鲁棒性。

有限控制集;模型预测控制;p-q理论;三电平逆变器;并联型有源电力滤波器

1 引言

目前，电流谐波治理的趋势是采用并联型有源电力滤波器(SAPF)。由于多电平逆变器具有输出容量大、适用于高压大功率场合、在没有增加开关器件负荷的基础上具有更多的电平数以及能有效降低谐波畸变率等优点，被广泛应用在SAPF的主电路拓扑结构中，其中最常见的是中点箝位式逆变器［1］。

中点箝位多电平逆变器的开关函数组合(控制集)个数有限，可以通过逆变器预测模型计算出所有开关函数组合分别作用下的系统输出，并选择使所设计的系统优化目标函数最小的开关函数组合作用于逆变器。该优化控制方法即为有限控制集模型预测控制，它具有动态响应速度快、计算量小、易于处理系统非线性和约束等优点，已经成为当前预测控制领域的主要研究方向。

本文首先给出基于有限控制集模型预测控制的SAPF的拓扑结构，然后具体研究了有限控制集模型预测控制器在中点箝位三电平逆变器中的控制原理和方法，并对基于p-q理论的参考电流计算方法以及用于预测负载电压和电流的重复预测器进行了详细分析。最后通过仿真及实验验证了该控制策略的有效性和可行性，证明该控制策略可提高SAPF的补偿性能。

2 SAPF的拓扑结构

有源电力滤波器(APF)是一种用于动态抑制谐波、补偿无功的新型电力电子装置。图1为并联型有源电力滤波装置，谐波源为非线性负载，由三相二极管不可控整流桥外接电感Ll与电阻Rl串联的阻感性负载组成。SAPF主电路采用中点箝位三电平逆变结构，接电感Lc和电阻Rc后并入电网。系统的控制部分主要由有限控制集模型预测控制器、参考电流计算模块以及重复预测器组成。

3 有限控制集模型预测控制策略

3.1 逆变器的控制方法

SAPF控制部分的核心是逆变器的控制，这里采用有限控制集模型预测控制器寻找出最优开关函数组合作用于逆变器，从而使补偿电流ic快速逼近参考电流。控制器设计的关键是根据逆变器的结构建立系统的预测模型。图2为中点箝位三电平电压源型逆变器的电路图。

图1 SAPF的拓扑结构Fig．1Topology structure of SAPF

图2 中点箝位三电平逆变器电路Fig．2Circuit of neutral point clamped three-level inverter

在公共耦合点(PCC)与逆变器直流侧电容器组成的闭合回路中应用基尔霍夫电压定律可得系统的状态空间模型为:

式中，ic为系统的补偿电流;Vload为公共耦合点上的电压，即负载端的等效电压;Vswitch为逆变器上的电压，其大小由开关函数组合与直流侧电容器上的电压决定。式(1)为连续状态空间模型，离散化后得到补偿电流的等效离散预测模型［2］:

式中，Ts为采样周期。

在逆变器的直流侧，每个电容器上的电压VCi(i =1，2)在连续时间内可以表示为:

式中，iDCi为流过电容器的电流，其大小由补偿电流ic和开关函数组合决定。式(3)离散化后得到电容器的等效离散电压预测模型:

中点箝位三相三电平逆变器合成电压矢量数为33=27种，除去冗余电压矢量，有效电压矢量为19种。为了选择最优开关函数组合，定义目标函数如下:

式中，iref为系统的参考电流;cp为当前开关函数组合转移到下一个开关函数组合所涉及的开关转换次数。

当系统工作时，逆变器的最优开关函数组合可以使系统优化目标函数最小，而最优开关函数组合的选择需要在减小电流跟踪误差、降低逆变器开关损耗和减少直流侧电容器的电压不均衡现象之间进行权衡，式(5)中的系数μ1和μ2决定了这三者的折中程度。

在实际应用过程中，控制器在测量和计算时存在一定的延时，因此需要预测逆变器超前两拍的最优开关函数组合。采用有限控制集模型预测控制策略，其具体过程为:

(1)在tk时刻，设作用在逆变器上的开关函数组合S(tk)已由tk－1时刻计算出，并且已测量出了系统的补偿电流ic(tk)、负载电压Vload(tk)以及逆变器直流侧每个电容器上的电压VCi(tk)。

(2)第一步预测:利用式(2)预测出系统超前一拍的补偿电流ic(tk+1)，并利用式(4)预测逆变器直流侧每个电容器上的电压VCi(tk+1)。

(3)第二步预测:计算系统超前两拍的补偿电流ic(tk+2)和逆变器直流侧每个电容器上的电压VCi(tk+2)，计算公式分别为:

(4)按如下公式计算出所有开关组合函数(27个)，然后选择使得在tk+2时刻系统优化目标函数最小的开关函数组合，也即tk+1时刻的最优开关函数组合S(tk+1)，并在tk+1时刻作用于逆变器。

3.2 参考电流的获取

为了使SAPF具有更好的补偿性能，参考电流的准确获取也十分重要。本文利用p-q理论来计算补偿电流超前两拍的参考值［3］，具体方法如图3所示。首先将三相负载电压与电流经过Clark变换投影到静止的α-β坐标系中，得到三相瞬时电压矢量和电流矢量。然后经过瞬时功率计算，得到瞬时实功功率p和瞬时虚功功率q。这两个功率中都含有一个恒定的直流分量和一个振荡的交流分量，即:

图3 基于p-q理论的参考电流获取方法Fig．3Method for obtaining reference current based on p-q theory

由于开关损耗和补偿功率的计算误差，逆变器直流侧需要与电网之间进行功率交换，这就导致直流侧电容器的电压不均衡，并且会降低SAPF的补偿效果。通过补偿图3中的功率可以使逆变器直流侧的电压幅值保持恒定不变。为了准确计算功率，逆变器直流侧的实际电压与参考电压进行了PI反馈调节，计算出的功率珋loss作为α-β电流计算公式中－的一部分。

3.3 负载电压和电流的预测方法

为了获得补偿电流超前两拍的参考值，需要利用重复预测器对负载电压和电流进行超前两拍的预测。重复预测器由线性预测器并联重复误差补偿器组成，前者对负载电压和电流进行超前两拍的预测，后者的作用是存储线性预测器tk时刻的误差，然后在tk+1时刻的线性预测中进行补偿。其整体结构如图4所示［4］，预测公式如下:

式中，x表示负载的电压或电流值;w表示x的线性预测值;d表示x在线性预测时需要补偿的误差。式(10)的闭环传递函数为:

式中，1．5－0．5z－1表示线性预测结果;用来补偿前一次线性预测的误差，其中的Q(z，z－1)为可以滤除高频测量噪声的一阶低通滤波器;N为一个周期内的采样次数。式(11)在离散时间系统中可以表示为:

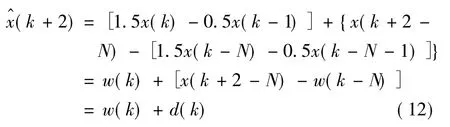
式中，滤波器Q(z，z－1)可以简化为1;d(x)为前一个周期中x的预测值与实际值之间的误差，作用于当前周期的线性预测器。由于负载具有周期特性，误差d(x)会逐渐减小。

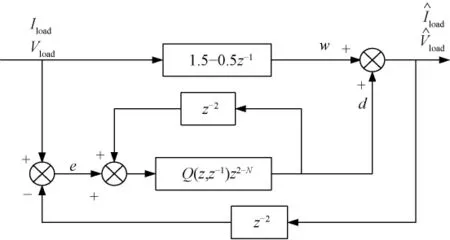
图4 重复预测器结构图Fig．4Diagram of repetitive predictor

在上述预测方法中，线性预测器与重复误差补偿器具有互补关系。线性预测器的响应速度快，但是没有记忆功能，且容易出现错误。为了提高预测精度，重复误差补偿器将先前的预测值存储起来，然后在下一次的线性预测中进行补偿，保证了零稳态跟踪误差。它的补偿时间稍长，但在线性预测器响应下一个动作之前能够使误差最小化［5］。

4 仿真分析

利用MATLAB对基于有限控制集模型预测控制的SAPF进行仿真研究，仿真参数设置如下:电源相电压有效值为110V，f=50Hz;电网侧Ls= 0.5mH;补偿端Rc=0.1Ω，Lc=10.5mH;负载Rl= 75Ω，Ll=20mH;系统采样周期Ts=40μs;逆变器直流侧的电容器由两个100V的直流电压源代替。图3中的滤波器选用截止频率为50Hz、阻尼因数为0.707的二阶低通滤波器。负载电压和电流预测过程中的高频测量噪声可以忽略，滤波器Q(z，z－1)等效为1。式(8)中的系数设为μ1=μ2=0.12，可以减小逆变器的开关损耗。

在有限控制集模型预测控制方法中，由于逆变器的开关频率不连续，其平均开关频率fave在三电平逆变器中由12个开关管的开关频率决定，即［6］:

式中，fi，j表示每个IGBT的开关频率。当系数μ1= μ2=0.12时，逆变器的平均开关频率为fave= 5.39Hz。

以A相为例，为了测试有限控制集模型预测控制方法在负载变化时的响应速度，在0.1s处使负载端的Rl由150Ω降到75Ω。负载电流Iload、补偿电流ic以及补偿后的电网电流Is如图5所示。经过计算，补偿后电网电流的总谐波畸变率由29.36%降为4.17%，系统的响应速度快，实时性好［7］。图5(d)为利用传统的电流跟踪PWM控制方法对系统的仿真结果，通过对比可知，有限控制集模型预测控制方法的补偿效果明显优于电流跟踪PWM控制方法。根据式(13)计算该控制方法的平均开关频率为5.46Hz，近似等于5.39Hz，但是总谐波畸变率为7.34%，大于4.17%。

下面对逆变器直流侧电压的控制方法进行仿真。电容C1=C2=50μF，系数μ1=μ2=0.1，经过PI控制器调节后，直流侧的总电压如图6所示，0.02s以后电压趋于稳定状态。

5 实验测试

图5 仿真波形Fig．5Simulation waveforms

图6 逆变器直流侧电压仿真Fig．6Simulation of inverter DC side voltage

为了验证SAPF的拓扑结构和控制策略的正确性与可行性，利用实验室开发的380V谐波电源和一套有源电力滤波装置进行样机实验。该装置的检测电路和控制电路由高速数字信号处理芯片DSP2812+CPLD和MAX125模数转换芯片以及相应的外围电路组成，开关管IGBT选择英飞凌BSM50GB120DN2模块(1.2kV，78A)，由三块落木源TX-DA962BA四单元IGBT驱动板进行驱动。逆变器直流侧电压为800V，由四个2200μF/450V电容两两并联后再串联组成，补偿端电阻Rc取0.8Ω，电感Lc取7.5mH。

电网的谐波电流由三相二极管不可控整流桥外接15mH与100Ω串联的阻感性负载组成的模拟谐波源产生，其中5、7次谐波含量较高，采用本文提出的控制策略对谐波电流进行跟踪控制，测试了A相电流补偿前后的波形及柱状图，如图7所示。可以看出，补偿后的A相电流接近正弦波，且电流总畸变率降到了2.5%，低于国家标准值5%。

图7 实验波形Fig．7Experimental waveforms

6 结论

本文以有效治理电网谐波问题为出发点，通过对基于中点箝位三电平逆变器拓扑结构的SAPF的分析，采用一种有限控制集模型预测控制策略在谐波电流补偿过程中进行优化控制，选择最优开关函数组合作用于逆变器，使补偿后的电网波形更接近于正弦波。最后对系统进行了仿真分析和实验测试，结果表明采用该控制策略的SAPF不仅具有鲁棒性好、响应速度快的优点，而且补偿效果明显，很好地改善了电网的电能质量。

［1］Rodriguez J，Bernet S，Steimer P，et al．A survey on neutral-point-clamped inverters［J］．IEEE Transactions on Industrial Electronics，2010，55(7):2219-2230．

［2］李玉玲，王克柔，林辉品，等(Li Yuling，Wang Kerou，Lin Huipin，et al．)．三相Boost并网逆变器的离散时间预测控制(The discrete-time predictive control of three-phase Boost grid-connected inverter)［J］．中国电机工程学报(Proceedings of the CSEE)，2011，31 (15):22-26．

［3］王晓鹏，韦寿祺(Wang Xiaopeng，Wei Shouqi)．一种基于P-Q理论的谐波电流检测方法的研究(A study of harmonic current detection based on P-Q theory)［J］．电子技术应用(Application of Electronic Technology)，2011，37(12):63-65．

［4］Rodriguez J，Pontt J，Silva C，et al．Predictive control of three-phase inverter［J］．Electronics Letters，2004，40 (9):561-562．

［5］Cao R，Low K S．A repetitive model predictive control approach for precision tracking of a linear motion system［J］．IEEE Transactions on Industrial Electronics，2009，56(6):1955-1962．

［6］Vargas R，Cortes P，Ammann U，et al．Predictive control of a three-phase neutral-point-clamped inverter［J］．IEEE Transactions on Industrial Electronics，2007，54 (5):2697-2705．

［7］陈良，黄传金，曹文思，等(Chen Liang，Huang Chuanjin，Cao Wensi，et al．)．三相四线制APF电流预测算法控制策略仿真(Research on three-phase fourwire APF based on prediction current control strategy)［J］．科学技术与工程(Science Technology and Engineering)，2012，12(22):5469-5473．

Research on SAPF based on finite control set model predictive control

WANG Yu-feng1，ZHOU Hong-yan1，LIU Cun-guo2，MENG Na1
(1．Faculty of Electrical and Control Engineering，Liaoning Technical University，Huludao 125105，China; 2．Fuxin Power Supply Company of Liaoning Power Co．Ltd．，Fuxin 123000，China)

In order to track and compensate the grid harmonic current quickly and accurately in the process of dynamic compensation harmonic for shunt active power filter(SAPF)，the SAPF that based on the topology structure of neutral point clamped three-level inverter is analyzed，and a finite control set model predictive control strategy is proposed．Firstly，the load voltage and current are predicted in two steps ahead by the repetitive predictor，and then according to these predictions，the reference value of compensation current is computed in two steps ahead through p-q theory．The simulation results show that the SAPF controlled by the finite control set model predictive control strategy can reduce the total harmonic distortion of grid current effectively，and has good compensation performance and robustness．

finite control set;model predictive control;p-q theory;three-level inverter;shunt active power filter

TN713

A

1003-3076(2015)02-0050-05

2013-05-10

辽宁省创新团队基金(2008T079)资助项目

汪玉凤(1962-)，女，河北籍，教授，博士生导师，研究领域为电力电子与电力传动;周宏胭(1988-)，女，河南籍，硕士研究生，研究方向为电力电子与电力传动。