波浪与非均匀透空外壁双筒柱的相互作用

于 过 曹孙林 赵 蓉

(大连理工大学建设工程学部，辽宁 大连 116024)

波浪与非均匀透空外壁双筒柱的相互作用

于 过 曹孙林 赵 蓉

(大连理工大学建设工程学部，辽宁 大连 116024)

简述了开孔结构所具有的良好特性，并采用比例边界有限元法进行了短峰波与非均匀透空外壁双筒柱的相互作用分析，为非均匀透空外壁双筒柱的水动力分析和结构设计提供了有价值的参考。

比例边界有限元，短峰波，波浪绕射，圆柱，非均匀开孔结构

0 引言

开孔结构作为一种新型海岸及港口工程结构物，具有以下良好特性：1)从水力学特性来讲，它既能降低波浪反射率，又可减少其所承受的波浪力；2)具有良好的受力特性；3)有可能降低造价，具有良好的经济指标[1]。然而，迄今为止，有关短峰波与非均匀透空外壁双筒柱相互作用的研究还很少。而且，一般的有限元方法也很难对波浪运动形式作出准确描述，但比例边界有限元方法能很好的描述该问题。

1 问题的提出

Φ(x,y,z,t)=φ(x,y)Z(z)e-iωt

(1)

满足边界条件的解为(k为波数)：

(2)

ω2=ghtanhkh

(3)

(4)

有限域Ω1和无限域Ω2界面处的边界条件可由式(5)表达：

(5)

其中，对于均匀开孔段的孔隙影响系数为G。当透空外壁为开口段时，开口段的孔隙影响系数为无穷大；而透空外壁为不透水壁时，G=0。

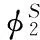
(6)

入射速度势φI可由式(7)表达[2]：

(7)

φ求出之后，波速度、波面高度和波动压力等可通过下列公式求得：

v=φ

(8)

(9)

p=-ρφ,t

(10)

2 推求比例边界有限元方程

SBFEM计算示意图见图2。

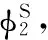
(11)

式(12)表示式(4)与式(11)的等效泛函变分：

(12)

空间直角坐标系与比例边界有限元坐标系之间的转换关系可表示为：

(13)

(14)

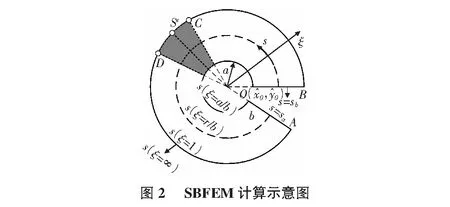
对两坐标系统分别求导，并用雅克比矩阵联系起来：

(15)

其中：

(16)

在比例边界坐标下，梯度算子可以表示为：

(17)

其中：

(18)

根据等参变换概念，速度势函数可采用同样的插值函数N(s)进行离散：

φ(ξ,s)=N(s)φ(ξ)

(19)

将式(17)和式(19)代入式(12)，经整理后可得：

(20)

其中：

B1(s)=b1(s)N(s),B2(s)=b2(s)N(s),s

(21)

引入下列系数矩阵E0,E1,E2,M0和Fs(ξ)[2]：

(22)

(23)

(24)

(25)

(26)

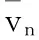
对式(20)中含δφ(ξ),ξ的项进行分部积分，并使ζ=kbξ，从而得到如下方程[2]：

(27)

(28)

(29)

3 求解比例边界有限元方程

3.1 求解无限域Ω2

式(27)是Bessel方程组，用Hri(ζ)Ti作为基函数表示其解：

(30)

其中，Hrj(ζ)被称为第一类汉克尔(Hankel)函数。

T=[T1,T2，…，Tn]

(31)

C=[c1,c2，…，cn]

(32)

(33)

将式(30)代入式(27)中，考虑到Hankel函数具有导数性质，经整理可得[2]：

(34)

因为Hankel函数已经满足无穷远处的边界条件，故只用对比例边界有限元在ξ=1上的边界条件进行考虑式(28)：

(35)

(36)

3.2 求解有限域Ω1并耦合Ω1和Ω2

同理，有限域Ω1中的φ1可用式(37)作为其解的基函数：

(37)

其中：

(38)

(39)

J(ζ)=diag[Jr1(kbξ),Jr2(kbξ),…,Jrn(kbξ)]

(40)

Y(ζ)=diag[Yr1(kbξ),Yr2(kbξ),…,Yrn(kbξ)]

(41)

考虑内边界条件式(28)、外边界条件式(29)分别可得Ω1中的SBFEM内外边界条件：

(42)

(43)

其中：

(44)

(45)

(46)

(47)

考虑方程(42)，方程(43)以方程(5)，得出：

(48)

可以解出两个域的解：

(49)

(50)

(51)

(52)

(53)

(54)

在式(53)中，i为虚实单位;G0为多孔介质的孔隙影响系数对角矩阵。

单位长度上力的大小可按式(55)计算[2](为方便起见，s代表x和y；r代表内外半径a和b；并且φx=cos(θ)，φy=sin(θ))：

(55)

总力的计算值可按式(56)求得：

(56)

由式(56)可以得出，归一化的Ps(kx,ky,k,r)在使用过程中会使问题更加简单。

4 结语

本文首次开展了应用比例边界有限元法对两种典型非均匀透空外壁(开口或不透水)双筒柱相互作用的研究，基于比例边界坐标变换和变分原理详细推导出一有限域和一无限域的SBFEM基本方程。总体来说，非均匀透空外壁中存在不透水段时，内外柱要承受更大的波浪力；平面波的作用力相对其他波来说也是最大的。本研究为工程上设计非均匀透空外壁双筒柱提供了理论参考。

[1] Huang Zhenhua, Li Yucheng, Liu Yong. Hydraulic performance and wave loadings of perforated/slotted coastal structures:A review[J].Ocean Engineering，2011,doi:10.1016/j.oceaneng,2011(3)：3-4.

[2] Tao Longbin, Song Hao, Chakrabarti Subrata. Scaled boundary FEM model for interaction of short-crested waves with a concentric porous cylindrical structure[J]. Journal of Waterway, Port, Coastal and Ocean Engineering,2009,135(5):200-212.

The interaction of waves and non-uniform open outer wall double cylinders

Yu Guo Cao Sunlin Zhao Rong

(FacultyofInfrastructureEngineering,DalianUniversityofTechnology,Dalian116024,China)

This paper simply introduced the good properties of open structure, and using proportion boundary finite element method made interaction analysis of short crested waves and non-uniform open outer wall double cylinders, provided valuable reference for hydrodynamic analysis and structure design of non-uniform open outer wall double cylinders.

proportion boundary finite element method, short crested waves, wave diffraction, cylindrical, non-uniform opening structure

2015-02-11

于 过(1994- )，男，在读本科生； 曹孙林(1994- )，男，在读本科生； 赵 蓉(1996- )，女，在读本科生

1009-6825(2015)13-0050-03

TU318

A