拉盖尔-高斯光束拓扑荷值的三角孔测量

李新忠，吕芳捷，王 辉，王屹山，聂兆刚

(1．河南科技大学 物理工程学院，河南 洛阳 471023；2．中国科学院西安光学精密机械研究所 瞬态光学与光子学国家重点实验室,陕西 西安 710119；3．新加坡南洋理工大学 数学物理学院，新加坡 新加坡 637371)



拉盖尔-高斯光束拓扑荷值的三角孔测量

李新忠1,2，吕芳捷1，王 辉1，王屹山2，聂兆刚3

(1．河南科技大学 物理工程学院，河南 洛阳 471023；2．中国科学院西安光学精密机械研究所 瞬态光学与光子学国家重点实验室,陕西 西安 710119；3．新加坡南洋理工大学 数学物理学院，新加坡 新加坡 637371)

基于三角孔衍射方法，测量了拉盖尔-高斯(LG)涡旋光束的拓扑荷值。当LG涡旋光束照射在三角孔衍射屏上后，在其后的傅里叶频谱面形成衍射三角点阵状光强分布；通过角点阵外边上衍射点数来确定拓扑荷值，拓扑荷的符号通过三角点阵的方向来确定。数值模拟和试验结果表明：该方法能有效测量LG光束的拓扑荷值，测量范围达到了±9。

衍射；光学涡旋；拓扑荷值；测量

0 引言

涡旋光束是一种具有螺旋形相位波前且中心光强为零的光束，其表达式中含有exp(imθ)的相位因子，其中m是涡旋光束的拓扑荷值[1-2]，每个光子携带mh的轨道角动量。涡旋光束的轨道角动量在量子信息编码[3-4]、光学扳手[5]、粒子旋转与操纵[6-7]等方面[8-10]具有重要的应用前景，因此，精确测量涡旋光束的拓扑荷值是涡旋光束研究中首要解决的科学问题。

从目前研究看，涡旋光束拓扑荷值的测量方法主要分为干涉测量[11-13]和衍射测量[14-20]。由于衍射方法光路简单，受到了众多研究者的关注，比较成功的有圆环衍射法[14]、环形椭圆孔衍射法[15]及锥透镜法[16]等。其中一项突出的工作是三角孔衍射法[17]，该方法测量拓扑荷值的范围为±7[18]，能实现半整数阶的拓扑荷值测量[19]。在衍射测量方法中，目前存在的最大问题是如何提高拓扑荷值的测量范围和测量准确性[12-13,18]。

本文利用三角孔衍射方法测量了典型涡旋光束—拉盖尔-高斯(LG)涡旋光束的拓扑荷值，通过精细调节光路，该方法能确定拓扑荷的大小和方向，拓扑荷值的测量范围扩展到了±9。此外，还研究了涡旋光束亮环尺寸与三角孔大小的匹配关系。

1 理论基础

拉盖尔-高斯光束作为一种典型的涡旋光束，在自然界中不存在。首先，要生成拉盖尔-高斯涡旋光束，本文采用了基于空间光调制器的计算全息法来生成LG光束。

鉴于本文的目的是测量LG光束的拓扑荷值，这里令LG光束的径向指数取0。设生成的LG光束在三角孔平面(z=0)的波场表达式为：

(1)

其中：m为角向指数，即拓扑荷数；(x0,y0)为三角孔平面内坐标；w0为照射在三角孔上的激光束的束腰尺寸；j为虚数单位。衍射屏采用边长为a的正三角孔，其复振幅透过率函数为：

(2)

当LG涡旋光束照射在三角孔屏上后，在夫琅禾费衍射区(傅里叶频谱面)的复振幅分布为：

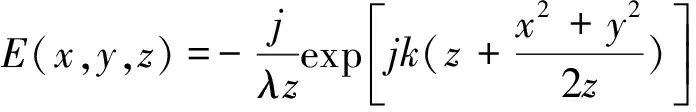
(3)

根据文献[17]的结论：通过傅里叶频谱面上的光强分布，即可判定涡旋光束拓扑荷值，即涡旋光束的拓扑荷值等于衍射点阵中最外侧边上点数减去1。

2 试验装置

Laser.激光器;BE.扩束器;P1,P2.偏振片;SLM.空间光调制器;A.光阑;T.三角孔；L.透镜;CCD.CCD相机；Computer.计算机。

试验光路原理图如图1所示。He-Ne激光器(λ=633 nm)产生的基模高斯光束经扩束准直后，入射到写入计算全息图的空间光调制器上，从空间光调制器出射后，生成LG涡旋光束。经可调光阑后选择+1级涡旋光束，然后使涡旋光束的暗核恰通过正三角孔照射在三角孔屏上。电荷耦合元件(CCD)相机置于透镜的焦平面，获得涡旋光束在夫琅禾费区的衍射光强图。

3 结果与讨论

利用三角孔衍射的方法来测量涡旋光束的拓扑荷值，其中一个关键问题是涡旋光束的亮环不能与三角孔的大小相差太多。首先，数值模拟和试验研究了涡旋光束亮环半径与拓扑荷值的关系，结果如图2和图3所示。其中，图2为数值模拟涡旋光束光强分布随拓扑荷值的变化。由图2可以看出：随着拓扑荷值的增大，LG光束亮环的直径也随之增大。

试验获得的LG涡旋光束光强分布图如图3所示。由图3可以看出：亮环的直径仍然随涡旋光束拓扑荷值的增大而增大。对试验图像来说，由于寄生干涉和光路的微失谐，导致光强图中圆环有部分干涉背景和变成圆度有所降低。但这对测量拓扑荷值来说，其影响可以忽略不计。

图2 不同拓扑荷值的LG光束模拟光强图图3 不同拓扑荷值的LG光束试验光强图

图4 涡旋光束经三角孔后的理论模拟图

为进一步验证该方法的有效性和拓扑荷值的测量范围，研究了拓扑荷值m=2～9的涡旋光束的衍射图案，图5为数值模拟结果。在图5中，m=2,4和m=6,8的涡旋光束三角形分别采用边长a=2mm和a=3mm。

图5 不同拓扑荷值的LG光束三角孔衍射模拟光强图

图6为拓扑荷值m=2～9的涡旋光束的试验衍射光强图，测试条件与模拟条件相同。由图6可以看出：试验结果与数值模拟结果符合的较好。在三角衍射点阵中，存在跳点现象，可能是由于本文采用的三角孔边不够光滑，边缘毛刺导致的刀口衍射所致。而在CCD相机拍摄过程中，存在光强饱和现象，因此三角衍射点阵的边界依然较为清晰。

图6 不同拓扑荷值的LG光束三角孔衍射试验光强图

而要在试验中获得更理想的衍射图案，需要制作更理想的三角孔，此外，还需要精细条件三角孔与涡旋光束亮环的相对位置，这是下一步工作的重点内容。

4 结论

利用三角孔衍射方法对LG光束的拓扑荷值进行了测量，拓扑荷值的绝对值等于衍射点阵三角形外边上亮点减去1。拓扑荷的符号可以通过衍射三角点阵的朝向来判断。此外，在测量过程中，三角孔的尺寸应与LG光束的亮环尺寸相匹配。要实现高拓扑荷值的测量，需要增大三角孔的尺寸，并精密调节三角孔与照射涡旋光束的相对位置。

[1] Allen L,Beijersbergen M W,Spreeuw R J C,et al.Orbital Angular Momentum of Light and the Transformation of Laguerre-Gaussian Laser Modes[J].Phys Rev A,1992,5(11):8185-8189.

[2] Allen L,Padgett M J,Babiker M.The Orbital Angular Momentum of Light[J].Prog Opt,1999,39:291-372.

[3] Leach J,padgett M J,Barnett S M,et al.Measuring the Orbital Angular Momentum of a Single Photon[J].Phys Rev Lett,2002,88:257901.

[4]Berkhout G C,Beijersbergen M W.Method for Probing the Orbital Angular Momentum of Optical Vortices in Electromagnetic Waves from Astronomical Objects[J].Phys Rev Lett,2008,101(10):100801.

[5] Molina T G,Torres J P,Torner L.Measuring of the Angular Momentum of Light:Preparation of Photons in Multidimensional Vector States of Angular Momentum[J].Phys Rev Lett,2002,88:013601.

[6] Ng J,Lin Z,Chan C T.Theory of Optical Trapping by an Optical Vortex Beam[J].Phys Rev Lett,2010,104:103601.

[7] Xia S Q,Song D H,Tang H Q,et al.Self-trapping and Oscillation of Quadruple Beams in High Band Gap of 2D Photonic Lattices[J].Opt Lett,2013,11:090801.

[8] Li X Z,Tai Y P,Nie Z N,et al.Propagation Properties of Optical Vortices in Random Speckle Field Based on Fresnel Diffraction Scheme[J].Opt Commu,2013,287(1):6-11.

[9] Yang Y,Dong Y,Zhao C,et al.Generation and Propagation of an Anomalous Vortex Beam[J].Opt Lett,2013,38:5418-5421.

[10] Yang Y,Dong Y,Zhao C,et al.Autocorrelation Properties of Fully Coherent Beam With and Without Orbital Angular Momentum[J].Opt Express,2014,22:2925-2932.

[11] Li X Z,Tai Y P,Lv F J,et al.Measuring the Fractional Topological Charge of LG Beams by Using Interference Intensity Analysis[J].Opt Commu,2015,334(1):235-239.

[12] Vaity P,Singh R P.Topological Charge Dependent Propagation of Optical Vortices Under Quadratic Phase Transformation[J].Opt Lett,2012,37:1301-1303.

[13] Vaity P,Banerji J,Singh R P.Measuring the Topological Charge of an Optical Vortex by Using a Tilted Convex Lens[J].Phys Lett A,2013,377:1154-1156.

[14] Guo C S,Lu L L,Wang H T.Characterizing Topological Charge of Optical Vortices by Using an Annular Aperture[J].Opt Lett,2009,34:3686-3688.

[15] Tao H,Liu Y,Chen Z,et al.Measuring the Topological Charge of Vortex Beams by Using an Annular Ellipse Aperture[J].Appl Phys B-Lasers O,2012,106:927-932.

[16] Han Y,Zhao G.Measuring the Topological Charge of Optical Vortices with an Axicon[J].Opt Lett,2011,36:2017-2019.

[17] Hickmann J M,Fonseca E J S,Soares W C,et al.Unveiling a Truncated Optical Lattice Associated with a Triangular Aperture Using Light’s Orbital Angular Momentum[J].Phys Rev Lett,2010,105:053904.

[18] de Araujo L E E,Anderson M E.Measuring Vortex Charge with a Triangular Aperture[J].Opt Lett,2011,36:787-789.

[19] Mourka A,Baumgartl J,Shanor C,et al.Visualization of the Birth of an Optical Vortex Using Diffraction from a Triangular Aperture[J].Opt Express,2011,19:5760-5771.

[20] Yang Y,Mazilu M,Dholakia K.Measuring the Orbital Angular Momentum of Partially Coherent Optical Vortices Through Singularities in Their Cross-spectral Density Functions[J].Opt Lett,2012,37:4949-4951.

国家自然科学基金项目(61205086,11404097);瞬态光学与光子学国家重点实验室开放基金项目(SKLST201203);河南省教育厅基金项目(12B140006)

李新忠(1979-),男,山东邹平人,副教授,博士,主要从事光电信息及其图像处理方面的研究.

2015-01-28

1672-6871(2015)04-0091-04

O436；O438.1

A