某跨海大桥运营期交通特性及荷载效应研究
朱 荣,石雪飞,阮 欣
(同济大学 桥梁工程系,上海 200092)
某跨海大桥运营期交通特性及荷载效应研究
朱 荣,石雪飞,阮 欣
(同济大学 桥梁工程系,上海 200092)
通过对某跨海大桥1个月的WIM数据进行统计,分析了运营阶段的交通组成特性及其规律,讨论了车辆荷载和车队荷载特性、多车道汽车荷载的横向分布规律。以该跨海大桥双塔三跨斜拉桥结构的关键截面为分析对象,研究了在实测车流荷载作用下的效应分布特征,并与现行设计规范的汽车效应标准值进行对比。结果显示:车头间距和时距与小时交通量呈现出二项指数函数关系;由于不同轴型车辆对行驶车道选择的倾向性,导致各车道汽车荷载水平分布存在明显的差异,单个重车车道效应极值大于规范值,而多车道总体效应小于规范值。探讨了现行规范在多车道荷载折减问题和大跨径桥梁汽车荷载效应计算模式上的不足与建议。
桥梁工程;动态称重;交通特性;车辆荷载;大跨径桥梁;效应分析
0 引 言
桥梁结构在运营期间面临的交通荷载环境是影响结构安全和使用寿命的重要 因素。近年来,随着我国公路交通运输事业的发展,交通量的增长、超载运输猖獗,已与相关的交通运输法规和现行规范不相协调[1]。在长期不合理的大比例重载交通作用下,桥梁的安全运营与耐久性受到威胁,并对桥梁运营养护及维修带来困难和沉重的经济负担。
运营期的交通特性统计和车辆荷载环境调查是对桥梁及其构件的实际工作性能评估的重要组成部分。目前,动态称重系统(Weigh-in-Motion,简称WIM)可以在车辆正常行驶的状态下记录通过观测断面的车辆信息,包括车速、车重、轴重、轴距以及车头时距和车头间距等交通特性参数,并在此基础上展开了相关的研究工作[2-4]。然而,以往的研究主要集中在总体车流特性的统计和中小跨径桥梁的效应分析上[5-6],对车辆荷载的车道分布规律和大跨径桥梁实际的汽车荷载效应特性关注不足,从而导致结构设计不合理。
笔者选取某跨海大桥为期1个月的WIM数据作为研究基础,该桥桥面布置为双向六车道,日均车流量达到2.6~3.4万辆,共计854 686辆车辆数据,该组数据在很大程度上能反映我国东部沿海地区经济社会活动特点,体现该区域交通运输的整体水平,且在大桥的运营期内具有一定的代表性。通过对交通流量、车型组成和车辆到达特性的统计,分析了交通组成特性及其规律;研究了车辆荷载和车队荷载特性,以及多车道汽车荷载的横向分布规律;以该跨海大桥为对象,分析了运营阶段实际的汽车荷载作用效应,并与现行设计规范进行比较,讨论了现行规范在多车道荷载折减问题和大跨径桥梁汽车荷载效应计算模式上的不足与建议,为桥梁设计以及桥梁运营阶段的管养工作提供借鉴。
1 交通组成特性
1.1 交通流量
交通流量为一段时间内通过的车辆实体数,反映道路桥梁的交通拥挤状况,具有一定的时变特性。统计时间内每天的交通量变化、周分布特性如图1,由图1可以看出,日均交通量为3.01万辆,变异系数为8%;由于我国实行周六、周日休息的5天工作日制,交通量在一周变化呈现出周五为峰值,周日为谷值的周期性变化规律,峰差约为20%。以每小时交通量反映车辆在一天内的密集分布状况,每小时平均车重反映车辆在各时段的荷载水平,进一步研究一天各时段内交通量与交通荷载的变化规律,如图2。
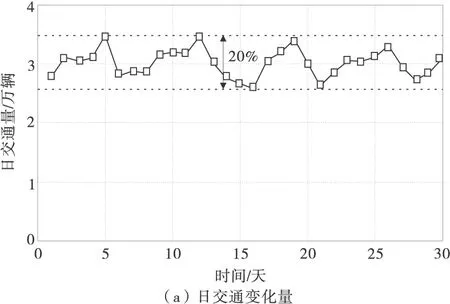

图1 日均交通量变化

图2 交通量和车重时变规律
图2表明,白天的车辆数要远远大于夜晚,交通高峰期出现在每天的9点至11点和14点至17点,低谷期出现在凌晨1点至5点。每一时段的平均车重与交通量呈现出相反的变化规律,交通量大的时段对应的车重并不是最大的。因此,对车流特性进行统计时,宜选用1~2周的整天数据进行分析。凌晨超重车辆出现的频率较高,是桥梁治超管理的重点时刻。
1.2 车型组成
公路桥梁上车型种类较多,对于单辆汽车,车重与轴数相关,以轴组作为划分车型的依据,将测得的车辆划为5类,各轴型车辆比例见表1。由表1可知,由于轻型客车(7座以下)数量较多,二轴车占的比例相当大,其次是六轴和三轴车;其中六轴的重车数量比较多,这类车型对桥梁的影响最为显著。进一步研究各轴型车辆对行驶车道选择的倾向性,图3为各轴型车辆在行驶车道上的分布比例。由图3可知,各轴型车辆有自己惯用的车道,二轴车由于质量较轻,偏向道路内侧的超车道行驶,三轴及以上轴型的车辆倾向道路外侧的慢车道。各轴型车辆对车道选择的倾向性引起的多车道荷载分布的差异将在2.3节中详述。
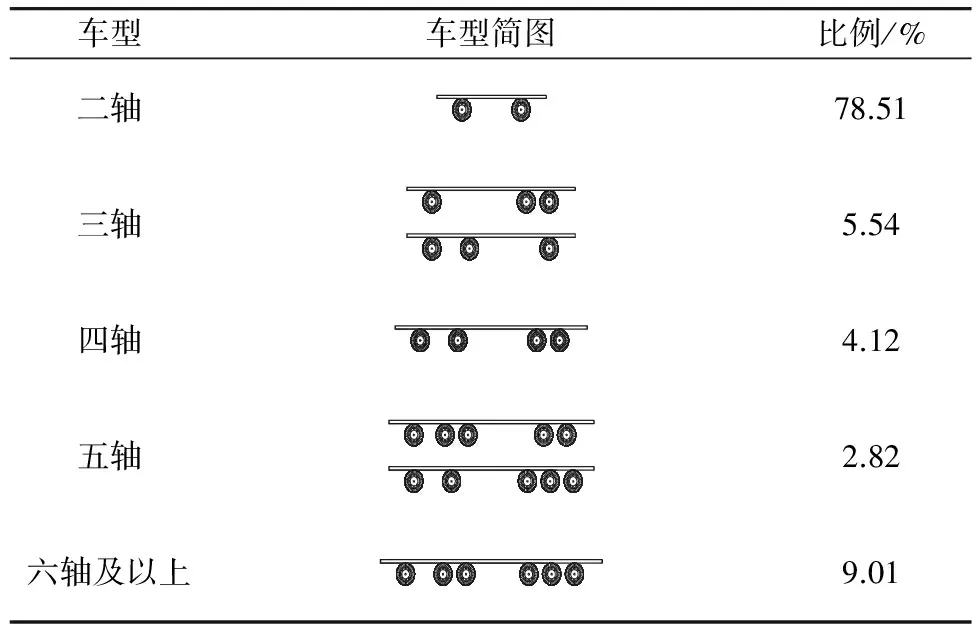
表1 车辆轴型分类及组成
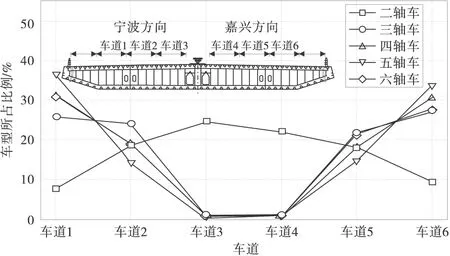
图3 各车道轴型车辆分布
1.3 车辆到达特性
车辆的到达特性也是反映车流疏密程度的重要指标,通常以车头时距和车头间距来衡量。为了说明该跨海大桥车流密集程度,沿引04规范基础数据[7]作为比较,车头时距和车头间距的累积分布曲线见图4。由图4可知,在同一累积概率水准下,车头时距小于04规范基础数据,反映交通量增长明显;相比之下,车头间距反而要大,这与高速公路的行车速度较快有关。


图4 车辆到达特性累积分布曲线
单独分析上述两特性不能充分反映车流密集程度,应与交通量联系在一起考虑。笔者研究了车辆到达特性与小时交通量之间的关系,对于总体车流而言,不考虑车辆对车道选择的倾向性,平均车头时距和平均车头间距与小时交通量关系如图5。从图5可见,随着交通量的增加,车头时距和车头间距急剧减小,到达一较大交通量(1 000辆/h)时,车辆的到达特性趋于平稳状态。两者均与小时交通量呈现出指数函数关系,可以通过二项指数函数来表达:
(1)


图5 车辆到达特性与交通量的关系
2 车流荷载特性
车流荷载特性主要包括荷载强度与荷载分布,涉及到车重、轴重、车速、车距、轴距等参数。对于不同跨径分类的桥梁结构,或者构件的整体和局部效应,汽车荷载强度与分布的考虑是不同的。中小跨径桥梁,一般以单个重车及多车道重车相遇概率控制[8-9],通过车重或轴重衡量荷载强度,轴距衡量荷载分布。而大跨径桥梁,单车的荷载效应占整个车队荷载效应比例不大[10],需要将交通量、车型组成,车辆间距、桥跨长度等因素综合考虑,以车队的形式衡量荷载强度和荷载分布。
2.1 车辆荷载
车重、轴重和轴距是描述单个车辆荷载特性的参数,与车型有关。已知车型载重、轴重和轴距的分布,可以根据结构的最不利加载位置计算荷载效应;对于直接承受荷载的桥面板等局部受力构件,轴重与轴距的影响就更为显著。各车型车重与轴重的统计参数见表2。

表2 车重与轴重统计参数
由表2可见,车辆总重随着轴数的增加而增大,标准差也逐渐增大;除了二轴车以外,其它车型车重的变异系数变化不明显。三轴及以上轴型车辆第一轴的轴重均值在5~6 t范围内,且标准差基本相同;不同轴组的轴重分布差异与各轴型车辆总重在车轴上分配比例有关,一般后轴轴重大于前轴,且分配比较平均,例如六轴车的三联轴各轴重均值在9 t左右,三联轴总重占车重的55%左右。
图6为车重与轴重的概率密度和累计概率分布图,通过与04规范基础数据的比较进一步说明大桥的运营荷载环境。从概率密度图形的分布来看,车重具有明显的三峰分布特性,由于小客车所占的比重较大,第一高峰出现在1~4 t范围内,且分布数量较多;第二、第三高峰出现在20和55 t左右。轴重分布呈现出双峰分布特征,第一峰值集中在4~6 t左右,主要为多轴货车前轴重量,第二峰值在10 t左右,为后联轴的单轴重量。


图6 车重与轴重概率密度和累计概率分布
由图6可见,当车重的累计概率小于0.68时,在同一概率水平下,现有的车重水平偏小,这是由于小型客车数量增多而引起的;但是当超越该概率水平时,车重远大于04规范基础数据,说明无论是重车的比例还是车重水平都较20世纪90年代初明显提高,在0.95概率水平下的车重数值为54 t,与之对应的规范基础数据数值仅为24 t。而轴重累计概率小于0.60时,现有轴重水平与04规范基础数据相当,但超越该概率水平后,现有轴重水平明显增大,在0.95概率水平下的轴重数值为14 t,与之对应的规范基础数据数值仅为8.5 t。
通过对车辆荷载特性分析可知,背景桥梁运营阶段的汽车荷载水平远大于设计规范界定的范围,虽然单辆重车对大跨径桥梁的效应不起控制作用,但是在“经常性”的大比例重载交通作用下,局部构件难免发生“疲劳性”损伤,从而影响结构的耐久性和使用安全,并增加养护维修成本。
2.2 车队荷载
在车队的组成中,车辆行驶状态是重要的影响因素,直接反映了车流密度,从结构效应层面上考虑,车流密度又决定效应加载范围内的荷载集度。现行规范[11]将公路-I、II级荷载分别对应密集和一般运行两种状态,以体现不同车流密度下的汽车荷载水平。笔者参考上述两种行驶状态的划分,并从新进行界定,一般运行状态以各车道实际的自然车间距进行排列,反映正常通行时的荷载水平;由于未录测到拥堵状况,密集运行状态以发生堵车时的车辆平均净距(4.5 m)[12]对白天数据进行排列,模拟发生交通事故时的极端状况。
为量化车队荷载,引入等效均布荷载(Equivalent uniformly distributed load,EUDL)[13]来分析不同结构效应加载长度的荷载集度,计算方法如下:首先,将连续车队满布在一定的桥跨范围内,使车队长度等于加载长度(图7),将长度范围内的所有车辆总重除以加载长度得到一等效均布荷载值。然后,移出车队首车,补充车队尾部车辆,使车队长度继续等于加载长度,计算得到新的等效均布荷载值。计算的加载长度范围从100至1 500 m,按照WIM数据中实测的车辆顺序对车队进行排列,分别考虑上述两种行驶状态。以最重车道的EUDL值进行分析,取保证率为95%的分位值,两种行驶状态的EUDL随桥跨长度变化见图8。


图7 等效均布荷载计算图示

图8 等效均布荷载值
与公路-I级荷载标准值进行对比来反映运营状况的车队荷载状态,从图8可知,随着加载长度的增加,车队的EUDL值逐渐减小并趋于稳定;车队在自然行驶状态时的荷载集度较小,在规范标准值的50%以下,加载跨径大于600 m时,小于规范值的25%;而在发生交通事故等拥堵状态时,车队的EUDL基本上维持在规范标准值1.6倍左右。
通过对量化车队荷载的EUDL值分析可知,虽然该路段交通量和超重车水平大于规范,但在一般运行状态下,各车道车队的整体车重水平比规范荷载值要偏低,能满足当前交通荷载环境下正常通行的安全需要。当发生堵车状况时,车队的整体车重水平明显提高,在日常桥梁管养和交通组织时,应密切注意交通拥堵发生的极端状况,及时有效地对重车进行分流,或采取封闭交通等措施,确保大桥的安全运营。
2.3 汽车荷载的横向分布特性
如前所述,不同类型车辆对车道选择具有一定的倾向性,这直接导致车辆荷载在车道分布上的差异,并影响桥梁结构的空间受力和道路路面疲劳损伤。
首先,对比不同行驶方向的各车型车重均值的差异,见表3。由表3可知,除二轴车外,上行车道车重水平比下行车道偏大10%左右,其差异性与地区产业布局和社会经济活动有关。表4比较了不同轴型车辆车重均值在各车道上的差异。由表4可知,中间车道各类车型的车重均值最大,其次为右侧车道,多轴车在中间和外侧车道的车重差异性较小;由于小型客车在超车道上的比例大,因此,超车道车重均值最小(1.62 t),其它轴型的重车偶尔也在超车道上行驶,但车重水平比外侧两个车道小20%左右。

表3 不同行驶方向各车型车重均值

表4 不同行驶车道各车型车重均值
分析车队荷载在不同车道上的分布规律,图9为两种行驶状态的车队EUDL值。由图9可知,超车道上的车队荷载较小,且随着加载跨径的增大变化不明显,即使在拥堵状态下,EUDL值基本维持在2.5 kN/m左右。外侧两车道在不同的行驶状态下的荷载分布特点略有不同,一般运行状态下,中间车道和右侧车道的EUDL相差不大(<5%),且随跨径增长荷载值迅速下降并趋于平缓;而在拥堵状态时,中间车道的EUDL比右侧车道偏小30%左右,且随跨径增长荷载值下降平缓。相比车重的分布规律,中间车道比右侧车道的EUDL小的原因是较轻的二轴车在中间车道所占比例较大(图3),车队组成略有不同,减小了整体的车队荷载。
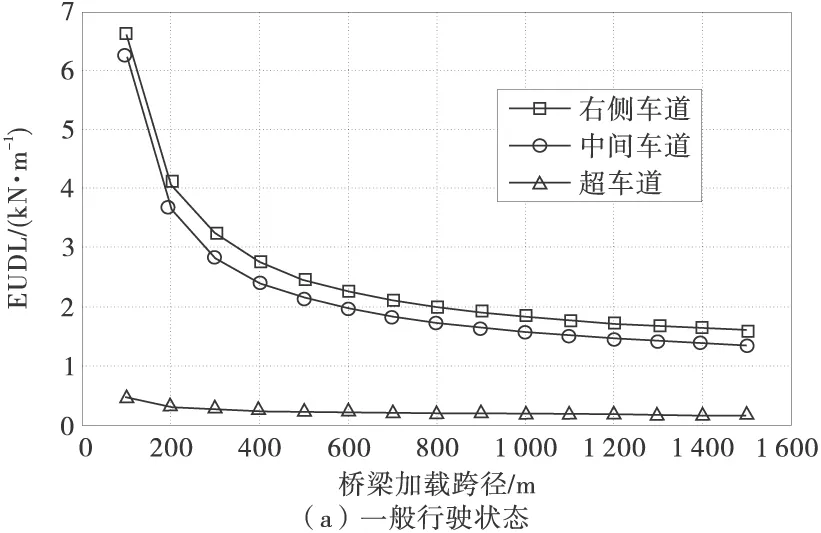
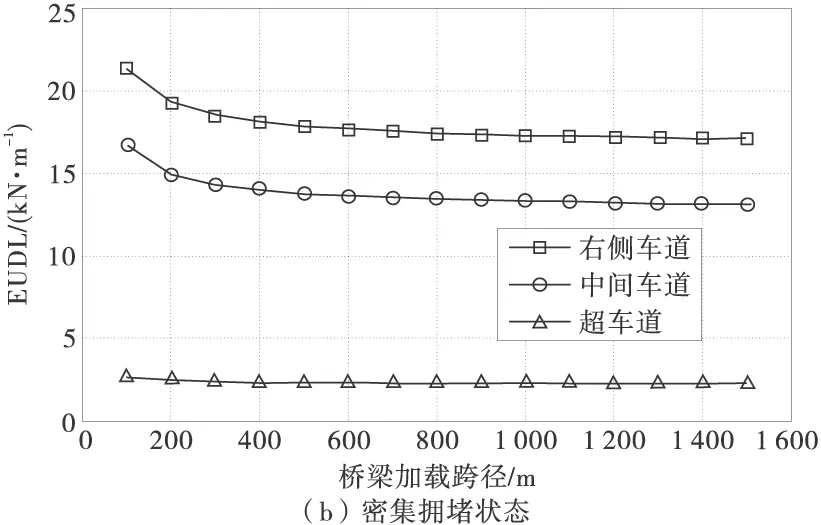
图9 不同行驶车道等效均布荷载
综上,对于双向六车道道路,各车道汽车荷载水平的分布存在明显的差异性,尤其是内侧超车道荷载水平普遍较低。相比我国规范中各车道汽车荷载独立同分布的假定,规范设计结果偏于安全,但其合理性有待效应分析后进行讨论。
3 实测汽车荷载下的结构效应分析
为研究桥梁结构在实际汽车荷载作用下的效应及其分布特点,针对该跨海大桥主桥的双塔三跨斜拉桥结构,选择一些控制结构总体性能的特征效应进行深入阐述,图10为确定的特征效应截面位置分布。沿用“公路桥梁可靠度研究课题组”的荷载效应计算方法和设计基准期最大荷载效应外推方法,得到了结构特征效应在各车道实测汽车荷载下的极值,见表5。

图10 结构特征效应截面位置
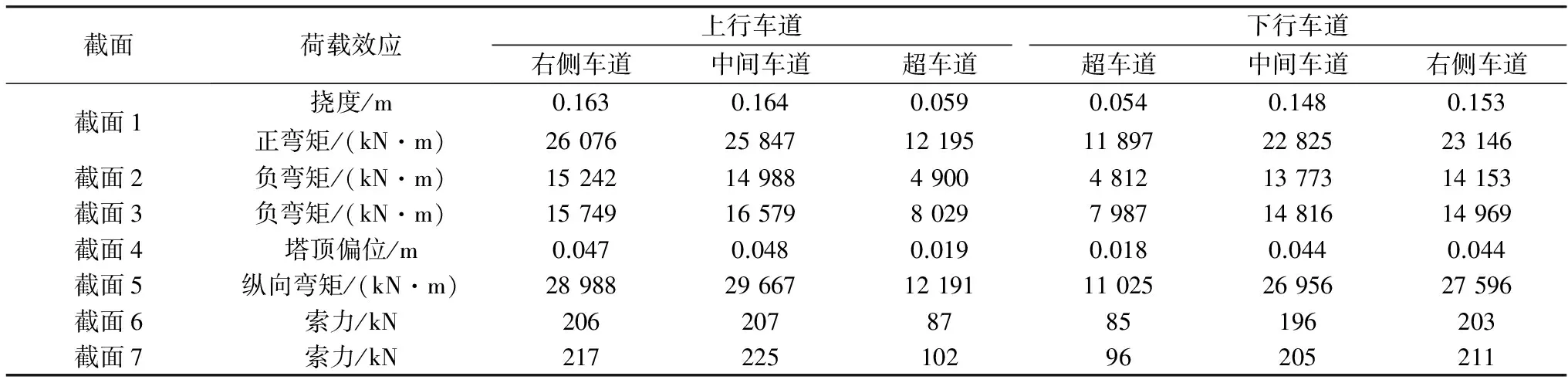
表5 各车道效应极值
由表5可知,下行车道效应极值小于上行所对应的车道,基本上能反映出上、下行车道车辆荷载的差异性。在同向行驶的车道中,右侧车道和中间车道的效应极值较大,且相互之间的差异性不明显(<5%);超车道的效应极值最小,不到外侧车道的50%。结合汽车荷载的特性可知,大跨径桥梁的荷载效应与车队的荷载水平相关,单辆重车对效应极值的影响并不显著。
实测汽车荷载最大单车道效应极值、六车道总体车流的效应极值与规范汽车荷载效应标准值的比较见图11(规范标准值为1),其中规范效应考虑了纵、横向的折减系数。图11表明,根据实际车流外推的最大单车道效应极值是规范值的1.0~1.8倍,相比六车道总体效应,反而小于规范值(0.5~0.7倍)。这意味着,规范在考虑横向多车道折减问题上作出的各车道交通量和车重独立同分布的假设使得总效应的取值偏于保守,未能反映车流荷载在各车道分布的差异性;由于货运普遍超载,使得重车车道的效应远远超过设计值,这对局部构件的损伤(路面铺装、钢桥面板疲劳)、耐久性可能构成隐患。因此,建议我国规范在对多车道效应折减时,考虑各车道荷载分布的差异性,可参考欧洲EUROCODE规范采用不同车道布置不同荷载的方式。

图11 效应极值与规范标准值比值
此外,大跨径桥梁的响应与汽车荷载取值和布置方式密切相关,具体表现在不同特征效应与设计值比值的差异性,直接承受汽车荷载的主梁,六车道总车流效应比在0.58~0.69之间,相比索塔墩底弯矩、塔顶偏位以及尾索索力的效应比(0.5以下)偏大,而后者更加关注车队加载的纵向不对称性。因此,在针对长加载跨径桥梁不同结构构件响应特点的基础上,结合车流特性,建立多级别多参数的汽车荷载模型[14],以体现设计结果的合理性与经济性。
4 结 论
通过对某跨海大桥运营阶段WIM数据分析,研究了桥梁交通组成及规律,讨论了车辆荷载和车队荷载特性、多车道汽车荷载的横向分布规律,以该跨海大桥的关键截面为例,分析在实测车流荷载作用下的效应特征,并与规范标准值进行比较,主要结论如下:
1)运营阶段的实际车流在交通量、车型组成方面具有一定的规律性。各轴型车辆对行驶车道的选择具有明显的倾向性;在车辆的到达特性中,平均车头间距和车头时距与小时交通量呈现出二项指数函数关系。
2)汽车荷载特性分析结果显示,运营阶段的交通量及超重车荷载水平远大于规范界定的范围,而考虑实际车队组成的等效均布荷载在不同行驶状态下荷载水平相差较大,一般运行状态下的车队整体车重水平比较规范荷载值要偏低(小于50%),堵车状态时在规范荷载值1.6倍左右。
3)多车道汽车荷载水平差异性分布明显,外侧车道几倍大于内侧超车道。结合大跨径桥梁结构的效应分析,单个重车车道的荷载效应大于规范值,而多车道总体效应小于规范值,表明目前规范对各车道交通量、车重独立同分布的考虑不充分,建议综合考虑多车道车流及荷载横向分布的差异性,对各车道荷载取值大小进行界定。
4)笔者通过特定地区交通数据的分析结果可能不具有普遍性,需要更多数据支撑加以完善。而相关的分析方法可对桥梁的运营荷载环境及结构技术状态进行评估,为桥梁养护决策提供数据支持,也为设计规范汽车荷载模型的完善和发展提供借鉴。
[1] 韩万水,闫君媛,武隽,等.基于长期监测的特重车交通荷载特性及动态过桥分析[J].中国公路学报,2014,27(2):54-61. Han Wanshui,Yan Junyuan,Wu Jun,et al.Extra-heavy truck load features and bridge dynamic response based on long-term traffic monitoring record [J].China Journal of Highway and Transport,2014,27(2):54-61.
[2] 陈艾荣,马如进,许艳梅.苏通大桥运营阶段车辆荷载识别及其特性[J].重庆交通大学学报:自然科学版,2013,32(增刊1):729-733. Chen Airong,Ma Rujin,Xu Yanmei.Vehicle loading identification and its characteristics of Sutong Bridge in operation [J].Journal of Chongqing Jiaotong University:Natural Science,2013,32 (Sup1):729- 733.
[3] 应天益.基于WIM数据的桥梁汽车荷载及其效应分析[D].上海:同济大学,2009. Ying Tianyi.Analysis on Traffic Load Effects on Bridges Based on WIM Data [D].Shanghai:Tongji University,2009.
[4] 李小年,陈艾荣,马如进.桥梁动态称重研究综述[J].土木工程学报,2013,46(3):79-85. Li Xiaonian,Chen Airong,Ma Rujin.Review of bridge weigh-in- motion [J].China Civil Engineering Journal,2013,46(3):79-85.
[5] 阮欣,周军勇,石雪飞.中法高速公路车流及荷载特性对比[J].同济大学学报:自然科学版,2013,41(9):1392-1397. Ruan Xin,Zhou Junyong,Shi Xuefei.Comparative study on highway traffic flow and load properties of China and France [J].Journal of Tongji University:Natural Science,2013,41(9):1392-1397.
[6] 张征文,杨飞,赵建峰,等.基于WIM数据的简支梁桥车辆荷载效应分析[J].公路交通科技,2014,31(5):86-92. Zhang Zhengwen,Yang Fei,Zhao Jianfeng,et al.Analysis on traffic load effect of simply supported beam bridge based on WIM data [J].Journal of Highway and Transportation Research and Development,2014,31(5):86-92.
[7] 李扬海,鲍卫刚,郭修武,等.公路桥梁结构可靠度与概率极限状态设计[M].北京:人民交通出版社,1997:88-96. Li Yanghai,Bao Weigang,Guo Xiuwu,et al.Structure Reliability and Probabilisatic Limit State Design for Highway Bridges [M].Beijing:China Communications Press,1997:88-96.
[8] Getachew A,Obrien E J.Simplified site-specific traffic load models for bridge assessment [J].Structure and Infrastructure Engineering,2007,3(4):303-311.
[9] 耿少波.在役中小跨径桥梁评估阶段汽车荷载模型技术研究[D].上海:同济大学,2012. Geng Shaobo.Vehicle Load Computation Model for Existing Medium and Short Span Bridges in Evaluation Phase [D].Shanghai:Tongji University,2012.
[10] Nowak A S,Lutomirska M,Sheikh Ibrahim F I.The development of live load for long span bridges [J].Bridge Structures-Assessment,Design & Construction,2010,6(1):73-79.
[11] JTG D 60—2004 公路桥涵设计通用规范[S].北京:人民交通出版社,2004. JTG D 60—2004 General Code for Desigh of Highway Bridges and Culverts [S].Beijing:China Communications Press,2004.
[12] Hwang E S,Lee K T,Kim D Y.Modelling of truck traffic for long span bridges [J].International Association for Bridge and Structural Engineering,2012,18(14):1112-1119.
[13] Lutomirska M.Live Load Models for Long Span Bridges [D].Lincoln:University of Nebraska,2009.
[14] 周军勇,石雪飞,阮欣.多塔斜拉桥汽车荷载总体响应分析[J].重庆交通大学学报:自然科学版,2013,32(增刊1):844-847. Zhou Junyong,Shi Xuefei,Ruan Xin.Overall vehicle load response of multi-pylon cable stayed bridge [J].Journal of Chongqing Jiaotong University:Natural Science,2013,32(Sup1):844-847.
Traffic Features and Load Effects of Cross-Sea Bridge in Service Period
Zhu Rong, Shi Xuefei, Ruan Xin
(Department of Bridge Engineering, Tongji University, Shanghai 200092, China)
Traffic composition features and laws for a certain cross-sea bridge in service period were analyzed based on a month WIM data. The vehicle and motorcade load properties as well as the load transverse distribution laws of multi-lane were described. Taking the critical sections of the three-span cable stayed bridge with twin towers as research object, the effect distribution characteristics resulting from the actual traffic load were analyzed statistically, and these effect results were compared with the normal values of vehicle loads in current bridge design specification. Results indicate that the relationship between the average space headway or time headway and hourly traffic volume can be expressed by the binomial exponential function. Vehicle load level on various driving lanes presents significant difference because of the tendency of vehicle lane-choice of different axial vehicle. The maximum effect values of the heaviest driving lane exceed the corresponding code values, while those of multi-lane are on the contrary. In the end, the insufficiencies of the multi-lane reduction factor and the calculation mode of vehicle load on large-span bridge in the current specification were discussed and some suggestions were also provided.
bridge engineering; weigh-in-motion; traffic feature; vehicle load; long span bridge; effect analysis
2014-11-27;
2015-01-07
国家自然科学基金项目(51108338;51478337)
朱 荣(1984—),男,江苏宝应人,博士研究生,主要从事桥梁工程方面的研究。E-mail:9arrom@tongji.edu.cn。
10.3969/j.issn.1674-0696.2015.06.01
U441+.2
A
1674-0696(2015)06-001-07

