基于CR列式的动力非线性有限元程序开发
王 涛,沈锐利
(西南交通大学 土木工程学院,四川 成都 610031)
基于CR列式的动力非线性有限元程序开发
王 涛,沈锐利
(西南交通大学 土木工程学院,四川 成都 610031)
基于CR列式非线性有限元计算理论,提出了针对杆、梁结构的Newmark-β非线性有限元动力时程积分算法,在动力时程计算中,可以考虑结构的几何非线性效应,通过计算单元伸长并扣除结构刚体位移得到单元的实际变形和内力;阐述了非线性有限元动力时程计算程序的计算原理,开发了计算程序,建立有限元模型;通过算例与ANSYS的计算结果进行了对比。结果表明:程序非线性静力与动力时程计算结果与ANSYS差别很小,且计算速度更快,程序算法正确可靠,适用于杆、梁结构大幅度非线性振动的计算。
桥梁工程;有限元程序;CR列式;几何非线性;动力时程;斜拉索
0 引 言
考虑结构几何非线性有限元计算方法是工程分析中的热点。对几何非线性,国内外学者提出了多种方法。最常用的是以结构变形前为参考,建立平衡方程的全拉格朗日法(TL列式法)和以结构变形后为参考,建立平衡方程的更新拉格朗日法(UL列式法)。K.J.Bathe等[1-2]在大量研究基础上,建立了三维梁单元大位移、大转动、小应变的UL列式和TL列式分析方法。陈政清等[3]改进了K.J.Bathe建立的非线性梁单元,提高了UL列式计算效率。
对于大转动问题,为了得到更为精确的结果,使用TL或UL列式往往需要增加荷载步,从而显著增加了计算时间,且因涉及到大转动问题,UL列式方法的推导过程往往都非常复杂,在实际编程的应用中难度较大。国内外广大学者对该问题其它解决途径进行了研究,流动坐标系方法——CR列式法(Co-rotational Formulation)成为了结构几何非线性有限元计算另一关注点。
G.A.Wempner等[4],T.Belytschko等[5]分别提出了CR列式的概念。A.Crisfield等[6]对不同单元几何非线性CR列式提出了一致列式方法。K.Hsiao等[7],C.A.Felippa等[8]对梁单元的CR列式计算方法进行了深入研究。周凌远等[9]将UL列式计算概念与CR列式方法结合起来,提出了基于UL法的CR列式三维梁单元计算方法。潘永仁[10],唐茂林[11]基于CR列式几何非线性计算方法开发了有限元程序,运用到大跨度悬索桥施工过程监控,取得了良好的结果。
以上研究主要关注结构静力计算几何非线性问题。目前,在结构动力时程计算中,通常使用振型分解法或线性Newmark-β法来得到结构的振动响应,对于结构的小幅度振动,线性分析方法尚能达到满足工程要求的精度,但当大跨度或柔性结构发生较大幅度振动时(特别是索结构),振动往往是非线性的,使用线性的计算方法得到的结果可能与实际情况偏差较大。
为了在动力时程计算中模拟结构的动态受力情况,笔者基于CR列式对单元内力的计算方法,建立了考虑结构几何非线性的Newmark-β动力时程计算方法,编制了计算程序,使用ANSYS验证了程序的正确性与可靠性。相对于一般基于UL列式几何非线性计算方法的商业通用有限元软件(如ANSYS等),该方法计算速度快,力学概念简洁(通常不必计算、推导复杂的单元非线性大位移刚度矩阵),适合于模拟柔性结构(特别是索结构)的大幅度非线性振动。
1 CR列式方法基本原理
以2维梁单元为例,在图1(a)中给出了在结构总体坐标系XY中未变形的二维梁单元,单元受到总体坐标系下的节点力以后,杆端的位移与转角如图1(b)。


图1 基于CR列式方法的单元计算示意
根据CR列式计算原理,在单元上附加一个流动坐标系X1Y1,流动坐标系原点始终位于单元i节点上,X1轴始终沿单元节点ij方向,Y1轴始终垂直于X1轴。
单元变形后,流动坐标系X1Y1位置与单元在流动坐标系内的伸长与转角如图1(b)。
对于图1(a)可以计算得到单元的长度与倾角:
(1)
对于图1(b)可以计算得到单元的长度与倾角:
(2)
对于梁单元,在单元流动坐标X1Y1中,单元节点的实际位移为单元伸长后的长度与初始长度的差。单元节点的实际转角为总体坐标系下节点的转角值减去单元在整体坐标系下发生的刚体转动值,显然,图1中刚体转动值为α2-α1。
对于平面梁单元,笔者使用了较为简单的刚体转动计算公式。刚体转动也可以根据单元变形前后X1轴基矢量的指向,使用矢量法则来计算[9-10]。
综上所述,如图1(b),在流动坐标系中,单元变形后的真实伸长与转角具体表达式为:
(3)
每一步迭代中梁单元在单元随动坐标系X1Y1中的节点的实际位移向量为:
{u}e={0 0 θi1uj10 θj1}
(4)
式(4)中,不计转动项,即为直杆单元的位移向量。由式(3)、式(4)可以看出,对于直杆单元,由于在流动坐标系中仅有X1轴方向的变形,使用CR列式方法计算得到的单元伸长在几何上是精确的。对于梁单元,得到的单元伸长,通过扣除刚体转动得到节点在单元坐标系内的转动值也是几何精确的。可以得到局部坐标系下单元实际内力:
{f}e=[k]e{u}e
(5)
式中:{f}e为单元内力的节点力向量;[k]e为单元弹性刚度矩阵。
一般情况下考虑结构几何非线性计算时,可认为整体结构处于大变形、大转动、小应变状态,那么在单元局部流动坐标系内可认为力与位移的关系是线性的,[k]e可取为线弹性的杆、梁单元矩阵[10-11]。
在非线性计算中,总体结构在外力作用下变形后的总体节点内力向量为位移的非线性函数,可表示为{R({u})},总体节点内力向量流程如图2。

图2 有限元模型总体节点内力向量计算流程
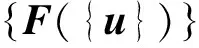

图3 有限元模型总体节点外力向量计算流程
根据图2与图3的计算流程,可以认为,在一般的CR列式算法中,结构在总体坐标系下,所有的几何非线性效应都是由位移造成的坐标转换矩阵的变化来反映的。由于CR列式为几何精确方法,所以从理论上来讲,荷载的分级加载的步数对最后结果无影响,差别来自于数值舍入的误差。
如果结构处于最终的静力平衡状态,则有:

(6)
对于式(6)可以使用迭代计算得到结构在外力作用下达到静力平衡状态时总体坐标系下各个节点的位移向量{u}。关于杆系CR列式非线性有限元静力计算方法的细节可以参考文献[9-11]。
2 基于CR列式的非线性有限元动力时程积分
2.1 基本理论
笔者开发了基于CR列式的非线性Newmark-β有限元动力时程积分方法,其基本假定与普通的Newmark-β法相同,可以写为:
(7)
(8)
其中各个参数具体表达式可以参见文献[12]。考虑几何非线性时,结构t+Δt时刻的振动方程为:
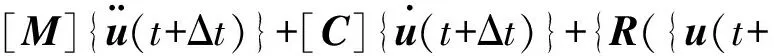
(9)
将式(7),式(8)代入式(9),可以得到:

(10)
这样,有限元非线性动力时程积分就转化为在每一个时间步内求解非线性方程组(10)的问题。
式(10)左端中的总体节点内力向量{R}是总体节点位移向量{u}的非线性函数。对于{R}可以按照图 2中的流程来计算 。
在考虑结构几何非线性时,式(10)右端中,{F}表示结构承受的总体节点外力向量,{Fe}表示结构初始单元力导致的等效总体节点外力向量(如ANSYS中初应变的概念),它们都是位移{u}的非线性函数,可以按照图3中的流程来计算。
式(10)左右两端还存在与总体质量矩阵[M] 、总体阻尼矩阵[C] 相关的等效力项。在非线性动力时程计算中,节点位置的变化必然会导致[M]的变化,所以在每一个时间步的计算中要根据当前节点位置使用坐标转换矩阵来更新[M]。对于阻尼,由于其复杂性,计算中不考虑[C]的变化。
可以使用牛顿迭代法来求解式(10),当迭代未收敛时,式(10)左右两端是不相等的,计算两端的差值就可以得到迭代的不平衡力。在迭代过程中使用的切线刚度矩阵为Newmark-β法等效总体刚度矩阵:
[K]=a0[M]+a1[C]+[Kk]
(11)
式中:[M],[C],[Kk]分别为将节点坐标更新到当前迭代步位置上时,结构的总体质量矩阵、总体阻尼矩阵、线性静力计算时计算的总体刚度矩阵。在计算中[Kk] 使用单元弹性刚度矩阵叠加单元应力刚度矩阵来组集。为了加快迭代计算收敛速度,式(11)也根据节点位置状态来更新。
2.2 单元计算
笔者使用的梁单元弹性刚度矩阵为:

(12)
式中:l0为单元的无应力长度;E为弹性模量;A为单元截面积;Iz为单元抗弯惯性矩。
若Iz=0则式(12)为平面杆单元的弹性刚度矩阵。若单元上存在轴力,则会产生应力刚度矩阵,在CR列式非线性计算迭代中,应力刚度矩阵一般起到加快收敛速度的作用,对最后的计算结果无影响[11]。梁单元应力刚度矩阵为:
(13)
式中:f为单元轴力。
(14)
式中:l为单元当前状态下的长度;ρ 为单元材料的质量密度。
杆单元应力刚度矩阵为:
(15)
杆单元一致质量矩阵为:
(16)
杆、梁单元的坐标转换矩阵为:
(17)
CR列式的非线性计算中,单元坐标转换矩阵是随着流动坐标系的变化而更新的。根据每一步迭代得到的位移值更新有限元模型节点坐标,再根据每个单元节点i, j的位置与单元长度l可计算得到:
(18)
2.3 算法流程
综上所述,笔者基于CR列式的几何非线性Newmark-β法有限元动力时程积分计算流程如图4。

图4 非线性有限元动力时程计算流程
为了更清晰地阐述笔者编程原理,使用了较为简单的平面杆、梁单元来构建程序。如需要使程序具有更广泛的适用性,可将程序扩展为三维空间非线性动力时程计算程序,编程思路与图4相同。
如果单元为三维空间杆单元,根据CR列式原理,只需要计算单元在三维空间的伸长便可以获得单元的实际内力。但对于梁、壳单元,三维空间中刚体转动情况是较为复杂的,为了计算三维单元扣除刚体转动的真实节点位移获得单元实际内力,通常要使用三维矢量代数公式来计算,文献[6-10]中较完整地讨论了这个问题 的技术解决方案。
笔者只阐述了使用的关键技术方法,更多的关于有限元程序开发技术,如:总体刚度矩阵组装、节点约束、节点自由度释放、节点耦合、矩阵求解、收敛条件判断、节点强制位移等可以参考文献[12]或其他关于有限元方法的著作。
3 算例验证
笔者使用MATLAB数值计算平台,开发了基于CR列式的杆系结构非线性动力有限元程序,程序特点如下:①可以考虑结构几何非线性计算结构的静力状态;②可以考虑结构大变形后的静力状态,计算结构的动力特性;③可以计算结构的非线性动力时程;④可以根据非线性动力时程计算结果绘制输出结构非线性振动的动画图形。
为了验证笔者程序的正确性与可靠性,将算例的结果与ANSYS计算结果进行对比。程序计算中的重力加速度均取为g=9.8 m/s2。计算中不设置结构阻尼,由文献[13]可知ANSYS计算中默认的算法阻尼不为0,即:Newmark-β法中γ=0.505,所以在本文程序计算中使用相同设置。ANSYS中分别使用Link1与 Beam3单元模拟平面杆、梁结构。
3.1 算例1
工程中常见的索-梁组合结构有限元模型如图5,主梁分为4个梁单元,拉索共分为10个直杆单元,弹性模量E、材料质量密度ρ,单元截面积A,梁单元抗弯刚度Iz,杆单元初始轴力H,单元物理参数如表1。

图5 索-梁组合结构有限元模型

表1 单元物理参数
考虑几何非线性计算结构在自重作用下的静力构型,得到ANSYS与笔者计算结果对比,如图6。


图6 索-梁组合结构静力计算ANSYS与本文程序计算结果
从图6可以看出,本文非线性静力计算结果与ANSYS差别很小。计算静力构型下的动力特性,得到结构前2阶模态如图7。

图7 结构前2阶模态
静力计算结果得到拉索的平均轴力为50.53 kN,由文献[14]的计算公式可以得到拉索局部的1阶自振频率为3.173 Hz。由图7及文献[14]可知,由于拉索的1阶自振频率接近整体结构的1阶自振频率,整体结构发生振动时,拉索会在端点位移激励(节点5)在拉索局部坐标系Y1方向的分量作用下发生1阶非线性主共振,文献[14]称之为索-梁相关振动。
在节点5上作用Y方向竖向力P=-10 kN,静力计算后释放节点力,动力时程积分取时间步长为0.02 s,分别使用ANSYS与本文程序计算结构在有自重状态下的振动时程[13],如图8。




图8 索-梁组合结构非线性振动ANSYS与本文程序计算结果
从图8可以看出,使用ANSYS计算的结果与本文计算得到的振动时程图是接近的。在释放节点力后结构发生了振动,索-梁相关振动[14]导致了拉索的共振,拉索端部约0.01 m幅值的位移激励,导致拉索中点发生了0.06 m的振动。结构振动体现了“拍振”的非线性振动性质[15],振动能量在拉索与整体结构之间互相传递,呈“此消彼长”的趋势。
如果程序存在错误,那么随着时间的发展,振动时程图的差别会变得更为明显。所以提取拉索1/2点(节点11)在30~40 s之间Y1方向振动时程对比ANSYS与本文程序计算结果,如图9。

图9 ANSYS与本文程序结果对比
从图9可以看出,对于30~40s时间段内节点11的振动时程,由于算法上的差别,笔者计算得到的振动幅值较ANSYS略微偏大,但两者的结果总体是很接近的,这说明了笔者程序的正确性。
3.2 算例2
某实际斜拉桥拉索(图10)的两端点直线距离l=112.775 m,倾角θ=24°,每延米质量m=60.1 kg/m,弹性模量E=1.96×1011Pa, 拉索初始轴力H=3 665 kN,截面积A=0.007 5 m2,拉索共分为20个直杆单元。

图10 斜拉索在端点位移激励下的有限元模型
考虑几何非线性计算拉索在自重作用下的静力构型,得到ANSYS与本文计算结果对比,如图11。


图11 拉索静力计算ANSYS与本文程序计算结果
从图11可以看出,本文非线性静力计算结果与ANSYS差别很小。计算拉索在静力构型下的动力特性,得到结构前2阶模态,如图12。

图12 拉索前2阶模态
如图10,设拉索端点位移激励U=ΔUsin(ωt) ,取端点位移激励幅值为ΔU=0.1 m,使用强制位移施加端点位移激励,激励频率ω为1.105×2=2.210 Hz ,动力时程积分时间步长取为0.02 s。
由于端点位移激励接近拉索的1阶自振频率的2倍,拉索会在端点位移激励X1方向分量作用下发生1阶参数主共振,拉索垂度较小,2阶频率接近1阶频率的2倍,拉索会在端点激励Y1方向分量作用下发生2阶主共振[15]。得到分别使用ANSYS与笔者程序计算拉索在有重力状态下1/4点(节点6)、1/2点(节点11)沿Y1方向振动时程,如图13。

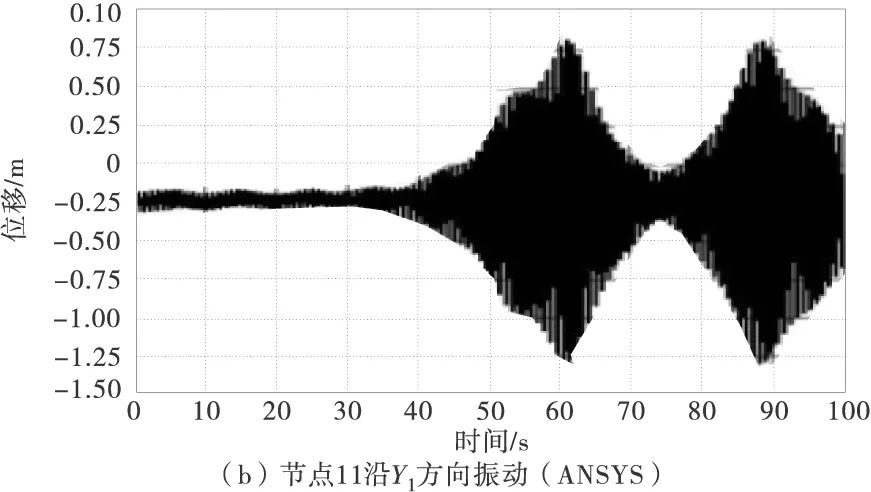
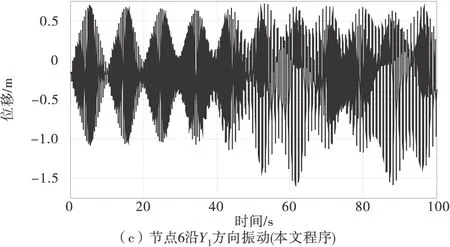
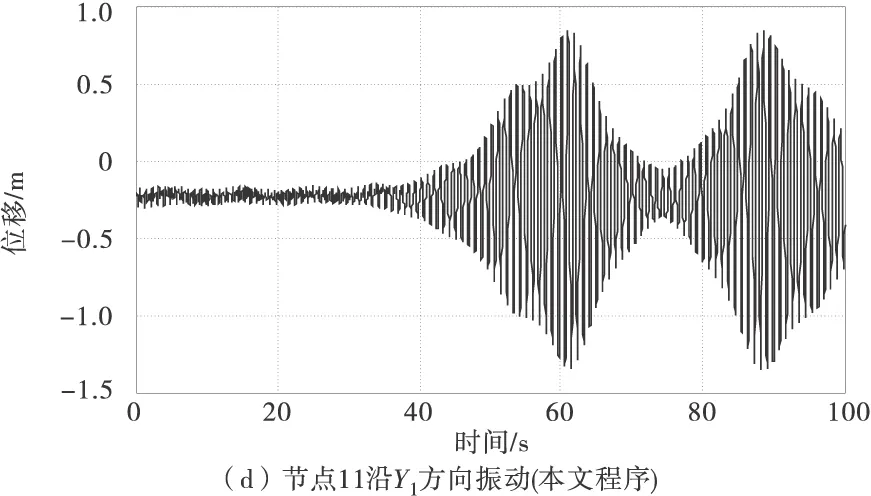
图13 拉索非线性振动ANSYS与本文程序计算结果
由图13可以看出,由于拉索上发生了2阶主共振与1阶参数共振,拉索1/4点与1/2点都发生了较大幅度的振动。提取90~100 s内拉索1/2点Y1方向振动时程,对比ANSYS与本文程序计算结果,如图14。

图14 ANSYS与本文程序结果对比
由图14可知,本文程序计算结果与ANSYS差别很小,验证了程序的正确性。
笔者程序可以根据计算结果生成振动时程的动画,可以更为直观地观察拉索非线性振动的发展过程,但限于表达方式,图15列出了拉索在各个时刻非线性振动的振动形状。
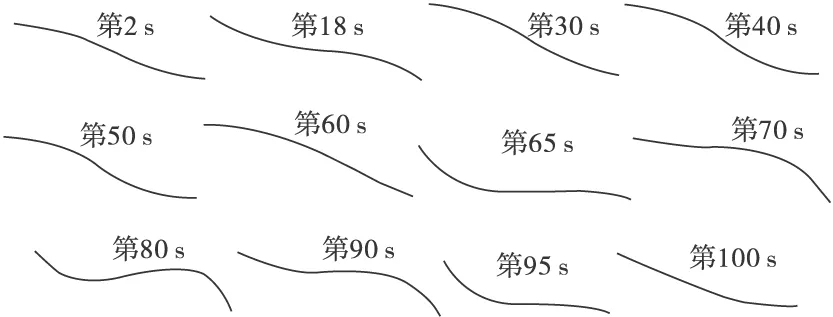
图15 拉索各个时间点振动形状(有放大)
由图15可以看出,拉索在端点位移激励作用下,首先发生了2阶主共振,随着时间的发展,拉索1/2点的振幅变大,拉索发生了1阶参数共振,这两种大幅度非线性振动在拉索上是同时存在的。
由于算例1、算例2均是计算结构在自重静力构型下的振动响应,所以结构静力变形后的状态为振动平衡位置,振动时程的初始位移不为0。
4 结 论
1)笔者提出了基于CR列式的非线性动力时程有限元算法,详细地阐述了程序开发过程。编制了有限元计算程序,通过算例的静力与动力计算与ANSYS结果的对比,验证了程序的正确、可靠性。
2)相对于ANSYS这样使用UL列式计算结构内力的通用软件,基于笔者算法开发的有限元程序具有更加简洁、实用、高效的特点。在算例1动力时程计算中,计算2 000步,使用ANSYS耗时约63 s,笔者程序耗时约18 s。在算例2动力时程计算中,由于使用了强制位移加载,计算5 000步ANSYS耗时约为430 s,笔者程序耗时约50 s。
3)本文程序可以计算在外力作用下柔性杆系结构的非线性振动,也可以计算结构在强制位移激励作用下的非线性振动。非线性有限元动力时程计算更好地反映了结构的受力细节。笔者方法为杆系结构非线性振动研究提供了较好的编程解决方案,适用于柔性结构,特别是索结构非线性振动的研究。
[1] Bathe K J,Ramm E,Wilson E L.Finite element formulations for large deformation dynamic analysis [J].International Journal for Numerical Methods and Engineering,1975,9(2):353-386.
[2] Bathe K J,Bolourchi S.Large displacement analysis of three-dimensional beam structures [J].International Journal for Numerical Methods and Engineering,1979,14(7):961-986.
[3] 陈政清,曾庆元,颜全胜.空间杆系结构大挠度问题内力分析的UL列式法[J].土木工程学报,1992,25(5):34-44. Chen Zhengqing,Zeng Qingyuan,Yan Quansheng.A UL formulation for internal force analysis of spatial frame structures with large displacement [J].China Civil Engineering Journal,1992,25(5):34-44.
[4] Wempner G A.Finite elements,finite rotations and small strains of flexible shells [J].International Journal of Solids and Structures,1969,5(7):117-153.
[5] Belytschko T,Hsieh B J.Non-linear transient finite element analysis with convected co-ordinates [J].International Journal for Numerical Methods and Engineering,1973,7(9):255-271.
[6] Crisfieldm A,Moita G F.A unified co-rotational framework for solids,shells and beams [J].International Journal of Solids and Structures,1996,33(24):2969-2992.
[7] Hsiao K,Linw Y.Co-rotational finite element formulation for buckling and post buckling analyses of spatial beams [J].Computer Methods in Applied Mechanics and Engineering,2000,188(3):567-594.
[8] Felippa C A,Haugen B.A unified formulation of small-strain co-rotational finite elements[ J].Theory Computer Methods in Applied Mechanics and Engineering,2005,194(19):2285-2 335.
[9] 周凌远,李乔.基于UL法的CR列式三维梁单元计算方法[J].西南交通大学学报,2006,41(6):690-695. Zhou Lingyuan,Li Qiao.Updated lagrangian co-rotational formulation for geometrically nonlinear FE analysis of 3-D beam element [J].Journal of Southwest Jiaotong University,2006,41(6):690-695.
[10] 潘永仁.悬索桥结构非线性分析理论与方法[M].北京:人民交通出版社,2001. Pan Yongren.Non-Linear Analysis Theory Method for Suspension Bridge Structure [M].Beijing:China Communications Press,2001.
[11] 唐茂林.大跨度悬索桥空间几何非线性分析与软件开发[D].成都:西南交通大学,2003. Tang Maolin.3D Geometric Nonlinear Analysis of Long-Span Suspension bridge and its Software Development [D].Chengdu:Southwest Jiaotong University,2003.
[12] 徐荣桥.结构分析的有限元法与MATLAB程序设计[M].北京:人民交通出版社,2006. Xu Rongqiao.Finite Element Method in Structural Analysis and MATLAB Programming [M].Beijing:China Communications Press,2006.
[13] 王新敏.ANSYS结构动力分析与应用[M].北京:人民交通出版社.2014. Wang Xinmin.Structural Dynamic Analysis and Application with ANSYS [M].Beijing:China Communications Press.2014.
[14] 王涛,沈锐利.斜拉桥索-梁相关振动概念与研究方法初探[J].振动与冲击,2013,20(32):29-34. Wang Tao,Shen Ruili.Primary investigation on the concept and method of cable-beam vibration in cable-stayed bridge [J].Journal of Vibration and Shock,2013,20(32):29-34.
[15] Nayfeh A.H,Mook D T.Nonlinear Oscillations [M].New York:Wiley Press,1984.
Developing of Dynamic Nonlinear Finite Element Method ProgramBased on Co-Rotational Formulation
Wang Tao, Shen Ruili
(School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, Sichuan, China)
Based on the nonlinear FEM computational theory of co-rotational (CR) formulation, a Newmark-βnonlinear FEM dynamic time-history algorithm for the structures of truss and beam was proposed. The geometric nonlinearity of the structures could be considered in the time-history calculation. The real displacement and internal force of the elements could be obtained by calculating the element extension and by deducting the rigid body displacement of the structure. The calculation principles of the geometric nonlinearity dynamic program were elaborated. A calculation program was developed and the FEM model was established. The comparison was carried out between the example and the calculation results of the ANSYS. The results show that the difference of the calculation results between the program and ANSYS on nonlinear static and dynamic time-history is very small, and the program is faster than ANSYS, which is applicative for large amplitude vibration calculation of truss and beam structures.
bridge engineering; FEM program; co-rotational formulation; geometric nonlinearity; dynamic time-history; stayed cable
10.3969/j.issn.1674-0696.2015.06.04
2014-08-12;
2015-04-14
国家自然科学基金项目(51178396)
王 涛(1983—), 男,四川南充人,博士研究生,主要从事桥梁结构动力学方面的研究。E-mail:7015294@qq.com。
U441;TB115
A
1674-0696(2015)06-019-08

