基于SEA法快速优化设计镁质复合前围板

郝志勇，丁政印

基于SEA法快速优化设计镁质复合前围板

郝志勇，丁政印

(浙江大学能源工程系，杭州 310027)

建立了包含27个子系统的前围板SEA(statistical energy analysis)法模型，通过理论计算确定了进行SEA分析所需的基本参数．求解隔声量并与试验结果对比，其吻合良好，验证了SEA法用来计算镁质前围板在高频段隔声量的有效性．根据各个子系统的声透射曲线可知，在高频段，有必要对前围板整个模型而非局部进行声学优化．据此优化设计了一种复合前围板．为了更加客观地评价其优化效果，提出用降噪效率作为前围板声学优化的一个综合评价指标．通过改变多孔吸声层和空气层的厚度，综合考虑降噪效率、车内空间的限制、轻量化和成本的要求，确定其最优方案的空气层为1,mm，多孔吸声层为10,mm．声学优化后的前围板较优化前隔声量平均提高了20.2,dB，这对工程实际应用具有十分重要的意义．

SEA法；隔声量；复合前围板；声学优化；降噪效率

传统的边界元和有限元方法只能适用于低频的振动噪声分析，中频问题多使用有限元与统计能量混合法[1-3]，至于高频段由于模态密度大，传统分析方法无法精确研究，因此SEA(statistical energy analysis)法应运而生，对其研究十分必要．SEA法作为一种统计分析方法，虽然尚不能精确预测某一点的响应，但可以准确地从统计意义上预测系统的平均声响应，常用于优化设计[4]．

目前，SEA方法已经成功用于分析夹芯板的传递损失[5]、双层板连接分析[6]以及能量传递路径研究等[7]．

镁质前围板相对于其他材质存在一定的优越性，处在驾驶室和发动机舱之间，是阻隔发动机噪声的主要构件，研究其声学性能十分必要．本文采用SEA法计算了镁质前围板高频段的隔声．与试验结果对比，验证了SEA模型的可靠性以及用此种方法计算镁合金复杂结构件隔声的有效性．通过对各个子系统的透射声功率分析，确定有必要对前围板整个模型采取优化措施，据此优化设计了多种复合前围板．为了综合评价其优化效果，提出用降噪效率作为评价指标；综合考虑车身轻量化和成本的要求，得到了改善隔声性能的最优方案．

1 SEA法基本理论

SEA法是一种统计性分析方法，使用能量流对系统的动力特性、振动响应及声辐射进行理论评估．图1给出了两个子系统的耦合功率流关系．其中

式中：ω 为频带的中心频率；12η代表能量从子系统1流到子系统2的耦合损耗因子；21η代表能量从子系统2流到子系统1的耦合损耗因子．

图1 两个子系统的耦合功率流Fig.1 Coupling power flow of two subsystems

对于保守系统，功率流动表现出可逆性．因此，子系统的模态密度1n、2n和耦合损耗因子12η、21η存在如下的关系：

将式(3)带入式(1)和式(2)中，得

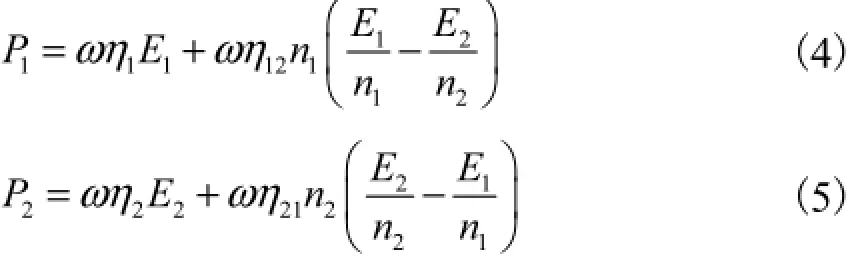
写成矩阵的形式为

式中：C为损耗因子构成的矩阵；E为能量阵；P为输入功率阵．

对于含有N个子系统的结构，有

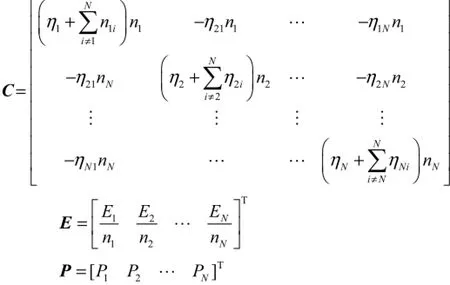
其中

式中：iP为外界对第i子系统输入的功率，i=1，2，…，N；in、jn、ijη和jiη分别为子系统i、j的模态密度和耦合损耗因子．

由上述推导SEA法基本方程的过程可知，如果子系统的模态密度、内损耗因子、系统间的耦合损耗因子以及外界对子系统的输入功率已知，求解方程，可计算出每个子系统的能量．能量表达式为

式中：m为结构子系统的质量；v2为振动速度在时间和空间上的平均；V为声学子系统的体积；p2为声压在时间和空间上的平均；ρ0为流体介质的密度；c为声音在介质中的传播速度．

通过联立SEA法基本方程和能量表达式，可求出所需要的振动级、声压级、应力等动力学参数．

2 前围板隔声试验

如图2所示，隔声量测试环境由2个相连的混响室和消声室构成，将前围板固定在混响室和消声室之间的窗口中，用氯丁橡胶条填充前围板和窗口之间的间隙，保证混响室的声激励只通过前围板传递到消声室中；同时使前围板接近自由边界条件状态，为声学仿真做准备；为防止声音通过穿孔泄露，导致无法精确地测量前围板隔声，在试验时用硅胶将其密封．

在混响室和消声室内分别布置传声器，消声室内各个测点分布在一个假想的包络住前围板的半球面上．测量混响室和消声室的平均声压pi、pt．隔声量TL为

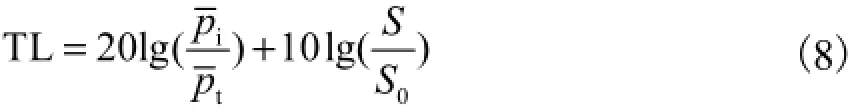
式中：S为前围板表面积；0S为消声室内假想包络面的面积．

图2 前围板隔声量试验环境Fig.2 Transmission loss test environment of dash panel

在发动机舱内，发动机辐射噪声以及其他各种噪声混合在一起，并且经过了多次反射和叠加，入射前围板噪声实际上是一个接近于混响的声场，故在对镁质前围板进行声学预测时在入射侧施加混响声源作为激励，更接近于实际情况．

3 前围板隔声仿真

3.1 SEA模型的建立

为了对前围板划分子系统，需要将前围板的有限元模型分割为不同的组集，如图3所示．根据模态相似原则划分为27个子系统，包括平板、单曲壳和双曲壳子系统．在生成的子系统一侧施加1,Pa的混响声源(DAF)作为激励，如图4(a)所示．前围板上的一些安装定位孔[8]在仿真时不用密封，因为DAF是定义在子系统上而不是在入射侧的空间内．在模型的两边各定义一个半无限流体场(SIF)[9]，用来接收透射声能．如图4(b)所示．镁合金材料参数与试验中的保持一致，将模型边界条件设为自由边界．

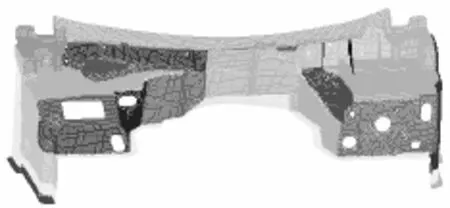
图3 前围板有限元模型Fig.3 Finite element model of dash panel

图4 前围板SEA模型Fig.4 SEA model of dash panel

3.2 SEA主要参数的确定

成功划分子系统后，要进行仿真分析，必须先确定SEA分析的主要参数，包括子系统的模态密度、内损耗因子以及子系统间的耦合损耗因子等．

对于模态密度，只要定义了子系统的属性，可用软件直接计算．

内损耗因子最为复杂，由3个彼此独立的阻尼机理构成，分别是结构损耗因子ηs、声辐射损耗因子ηr和边界阻尼损耗因子ηb，即η=ηs+ηr+ηb．对于车身薄壁件，子系统的内损耗因子通常受上述3个参数中的一个支配．前围板中所有子系统之间属于刚性连接，此时边界阻尼损耗因子较小，接近于0，可以忽略不计；同时，软件中对子系统之间施加线连接时，也指定为无损连接，即阻尼损耗因子为0，因此有η=ηs+ηr. ηs查阅资料可得，如玻璃的结构损耗因子为1×10-3，钢的结构损耗因子为3×10-4．ηr[10]为

式中：σ为振动结构声辐射效率；sρ为结构的面密度.

随机激励的有限板的声辐射效率σ的近似计算式[10]为

式中：Ar为声辐射的面积；Cr为振动结构的周长；λc为临界频率处的波长；fc为临界频率；β为平板边界条件系数，简支边β=1，固支边β=2，一般边界条件β=2，前围板中的子系统处于全约束的状态，β取一般边界条件2即可；h为板的厚度；ρ为板密度；μ为泊松比；Em为材料弹性模量．

内损耗因子随频率的变化而变化，实际应用中，当f≤fc时，将声辐射效率公式代入到式(9)中，即可得到声辐射损耗因子，加之查阅的结构损耗因子即为内损耗因子；当f＞fc时，由声辐射效率的计算公式可得出σ≈1，此时式(9)中的ω相对会很大，ηr计算结果很小，趋近于0，此时η≈ηs．

经验表明，在高频区域，内损耗因子以结构损耗因子ηs为主，故内损耗因子下限是结构损耗因子．

根据上述分析和经验，编制程序计算出某一子系统的内损耗因子，结果如图5所示．

图6 试验与仿真1/3倍频程下隔声量的对比Fig.6Comparison between test and simulation for transmission loss under 1/3 octave

由图6可以看出，SEA法预测的隔声量与试验结果能够很好地吻合．因为边界条件对高频段的影响很小，可以忽略不计，所以仿真可以很好地模拟实际情况．良好的吻合性验证了SEA法用来预测前围板高频段的隔声行之有效．

4 复合前围板优化设计

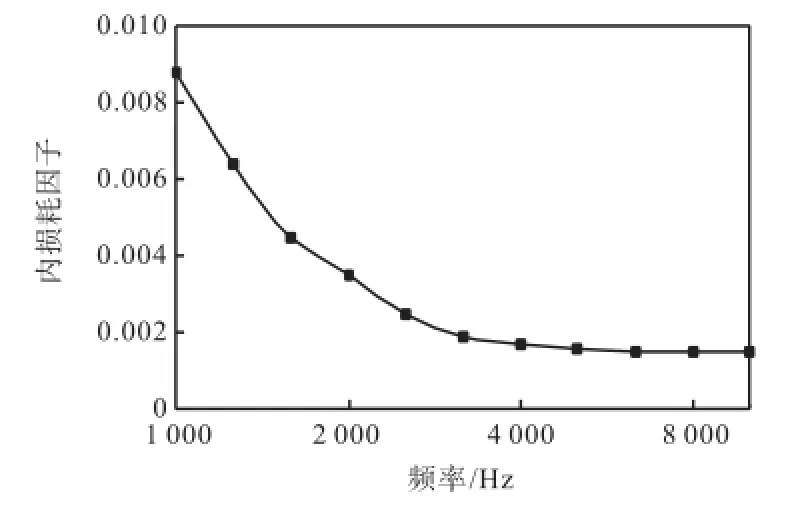
图5 子系统的内损耗因子Fig.5 Internal loss factor of subsystem

由SEA法求得前围板各个子系统的声透射，可知几乎所有的子系统对总的透射声功率贡献都比较大，因为在高频段，每个子系统的模态密度都比较密集，此时振动的响应是由局部模态控制，各个子系统的振动响应都比较严重，因此有必要对前围板整个模型进行声学优化，而非局部．

考虑到轻量化以及成本的要求，设计了一种以铺设声包装结构的复合前围板．设计方案如图7所示．

在软件中，子系统建立连接后，耦合损耗因子会自动根据连接来确定．

3.3 隔声量的求解

前围板的隔声量(传声损失)TL为

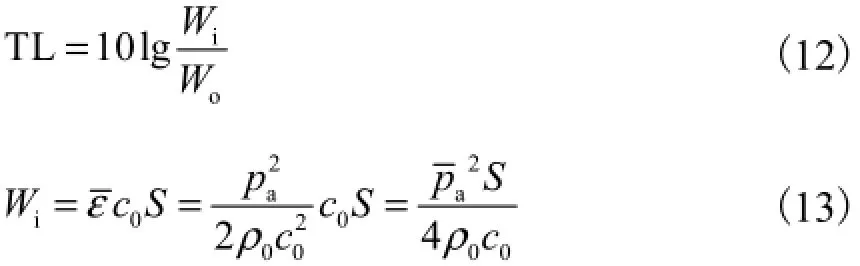
式中：Wi为前围板入射声功率[11]；Wo为透射侧声功率；pa为入射侧声压的幅值；pa为入射侧声压有效值；c0为声音在流体介质中的传播速度．

透射侧声功率Wo为多个SIF入射声功率的总和.

整理以上分析结果，获得试验和仿真在1/3倍频程下的隔声量曲线如图6所示．

图7 声学包装示意Fig.7 Schematic diagram of sound package

第1层为空气层．声学包装中的多孔吸声层和基板之间一般都有一定的空气隔层如汽车顶棚的声包装[12]．这样做主要是为了形成双层隔声结构，有效阻隔外部空气声的传递．

第2层为吸声层．主要是在前围板上安装多孔吸声材料，把声能变为热能耗散掉，从而达到吸收噪声的目的. 其流体介质为空气，流体密度为1.225,kg/m3，流体声速为340,m/s，孔隙率为0.95，流阻率5,000,Pa·s/m2，结构损耗因子为0.01，黏弹性特征长度为7×10-5,m，热力学特征长度为1.2×10-4,m，材料密度为64,kg/m3，弹性模量为2.85×104，泊松比为0.28．

第3层为均匀质量覆盖层，厚度为2,mm，面密度为4,kg/m2．其目的是便于搬运、装配和保持几何形状．

4.1 降噪效率

为了更加全面地评价各个优化方案的综合降噪效果，用降噪效率作为评价指标，定义为声压级降低的平均值与采取优化措施而增加质量的比值，即

式中：ξ为降噪效率，dB/kg；Lp为声压级降低的平均值，dB；m′为所采取降噪措施增加的质量，kg．

4.2 多孔吸声层厚度对前围板隔声量的影响

为了研究多孔吸声层厚度对隔声量的影响，将厚度在5～25,mm范围内改变，步长为5,mm，计算结果如图8所示．

图8 多孔吸声层厚度对隔声量的影响Fig.8 Effect of thickness of porous sound-absorbing layer on transmission loss

图8 表明，多孔吸声层厚度对TL在1～5,kHz频带上有显著影响且变化规律较为复杂．隔声量并不随厚度的增加而一直增加，主要是因为厚度增加到某一数值时，在某些频率处会引起前围板与声包装结构发生耦合，导致隔声量有所下降．为了综合评价各个方案的优化效果，做出各方案的降噪效率，如图9所示．

图9 多种方案降噪效率的对比Fig.9 Comparison of noise reduction efficiency for a variety of programs

随着多孔吸声层厚度的增加，降噪效率逐渐升高，但是不明显，综合考虑到车内空间的限制和车身轻量化以及成本的要求，选择10,mm多孔吸声层．

4.3 空气层厚度对前围板隔声量的影响

为获得最佳的声学优化方案，改变空气层厚度，研究其对隔声量的影响，整个分析过程中多孔吸声层厚度为10,mm，空气层的厚度在1～5,mm范围内改变，步长为1,mm，计算结果如图10所示．

图10 空气层厚度对隔声量的影响Fig.10 Effect of air layer thickness on transmission loss

由图10可以看出，空气层厚度的变化并不会导致前围板质量的增加，隔声量在1 000～2 000,Hz范围内最大变化为1,dB左右；其他频段内基本没有变化，致使声压级降低的平均值在各个方案下基本一致．根据降噪效率的定义可知，降噪效率维持不变，考虑到驾驶室空间的限制，决定选用1,mm厚的空气层．

根据以上分析，最终优化方案确定其空气层厚度为1,mm，多孔吸声层厚度为10,mm，均匀质量覆盖层厚度为2,mm．这样不仅可以有效地改善隔声性能，而且也最大化地增加了驾驶室的空间，降低了车身质量和成本．

根据仿真分析结果，做出声学优化前后的隔声量曲线，如图11所示．

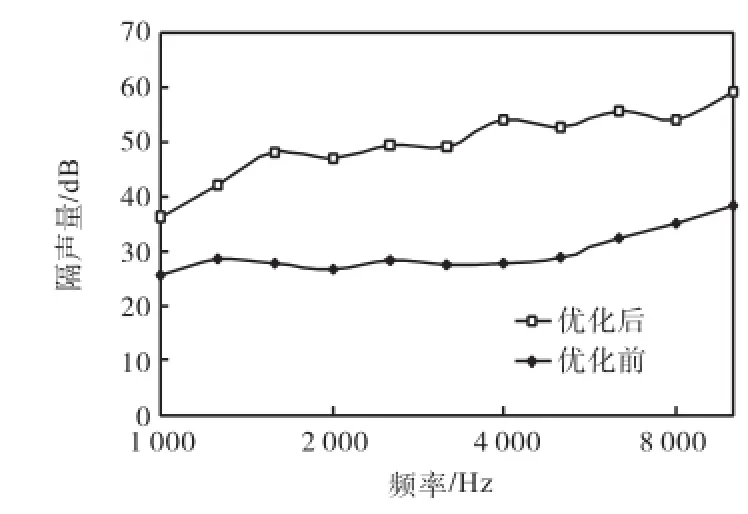
图11 声学优化前后隔声量的对比Fig.11Comparison of transmission loss before and after acoustic optimization

由图11可知，设计的声学优化方案很好地改善了前围板的隔声效果，使其在1/3倍频带内隔声量的声压级平均提高了20.2,dB．

5 结 论

(1) 建立了包含27个子系统的前围板SEA模型，通过理论计算确定了SEA分析的基本参数：模态密度、内损耗因子和耦合损耗因子．最后求解隔声量，与试验结果相比，吻合良好，验证了SEA法用来预测镁质前围板在高频段的隔声量行之有效．

(2) 为了更加客观地评价优化效果，提出用降噪效率作为前围板声学优化的一个综合评价指标．

(3) 根据各个子系统的声透射，在高频段有必要对前围板整个模型进行声学优化，而非局部．据此优化设计了多种复合前围板，通过改变多孔吸声层和空气层的厚度，综合考虑降噪效率、车内空间的限制以及轻量化和成本的要求，确定优化方案的空气层为1,mm，多孔吸声层为10,mm．

(4) 优化设计后的镁质复合前围板，其隔声量平均提高了20.2,dB，不仅有效地改善了隔声效果，而且也综合考虑了驾驶室空间、车身轻量化和成本的要求，对工程实际有着十分重要的意义．

［1］ Connelly T，Mattson S，Labyak D. Prediction of muffler insertion loss and shell noise by a hybrid finite element acoustic statistical energy analysis model[J]. Journal of the Acoustical Society of America，2010，127(3)：1796.

［2］ Vergote K，Genechten B V，Vandepitte D. On the analysis of vibro-acoustic systems in the mid-frequency range using a hybrid deterministic-statistical approach [J]. Computer and Structures，2011，89(11)：868-877.

［3］ Maksimov D N，Tanner G. A hybrid approach for predicting the distribution of vibro-acoustic energy in complex built-up structures[J]. Journal of the Acoustical Society of America，2011，130(3)：1337-1347.

［4］ Chavan T，Manik D N. Optimum design of vibroacoustic systems using SEA[J]. International Journal of Acoustics and Vibration，2008，13(2)：15-20.

［5］ Zhou Ran，Crocker M J. Sound transmission loss of foam-filled honeycomb sandwich panels using statistical energy analysis and theoretical and measured dynamic properties[J]. Journal of Sound and Vibration，2010，329(6)：673-686.

［6］ Hopkins C. Experimental statistical energy analysis of coupled plates with wave conversion at the junction[J]. Journal of Sound and Vibration，2009，322(1)：155-156.

［7］ Guasch O，Aragones A. Finding the dominant energy transmission paths in statistical energy analysis[J]. Journal of Sound and Vibration，2011，330(10)：2325-2338.

［8］ 陈家瑞. 汽车构造(下册)[M]. 北京：机械工业出版社，2009.

Chen Jiarui. Automobile Structure(Next Volume)[M]. Beijing：China Machine Press，2009(in Chinese).

［9］ France，VAone User Guide[EB/OL]. http：//www.esigroup.com，2013-08-25.

［10］ 陈 鑫. 基于SEA方法的轿车车内噪声分析与控制研究[D]. 长春：吉林大学汽车工程学院，2008.

Chen Xin. Research on Analysis and Control of Car Interior Noise Based on SEA Method[D]. Changchun：College of Automotive Engineering，Jilin University，2008(in Chinese).

［11］ 杜功焕，朱哲民，龚秀芬. 声学基础[M]. 3版. 南京：南京大学出版社，2001.

Du Gonghuan，Zhu Zhemin，Gong Xiufen. Acoustic Basis[M]. 3rd ed. Nanjing：Nanjing University Press，2001(in Chinese).

［12］ 庞 剑，何 华. 汽车噪声与振动：理论与应用[M].北京：北京理工大学出版社，2006.

Pang Jian，He Hua. Automotive Noise and Vibration：Principle and Application[M]. Beijing：Beijing Institute of Technology Press，2006(in Chinese).

(责任编辑：金顺爱)

Rapid Optimization and Design of Mag-Based Composite Dash Panel with SEA Method

Hao Zhiyong，Ding Zhengyin
(Department of Energy Engineering，Zhejiang University，Hangzhou 310027，China)

The dash panel SEA model containing 27 subsystems was established and the basic SEA parameters were determined by theoretical calculation. Comparison between the calculated transmission loss(TL)and the testresults showed that they fit well，which proved that the SEA method was feasible to calculate TL of mag-based dash panel in high frequency range. According to the sound transmission curve of the various subsystems，it was necessary to make acoustic optimization on the whole rather than part of the model of the dash panel in high frequency range. A composite dash panel was thus designed. For a more objective evaluation of its optimization effect，noise reduction efficiency was proposed to be used as a comprehensive evaluation index on dash panel sound package. With consideration of the noise reduction efficiency，the limit of the interior space，lightweight and cost requirements，the optimal thickness of the air layer is determined to be 1 mm and that of the porous sound-absorbing layer is 10 mm，after the thicknesses of the two layers have been changed several times. The TL increases by 20.2 dB on average after acoustic optimization，which is very significant in engineering application.

statistical energy analysis(SEA) method；transmission loss(TL)；composite dash panel；acoustic optimization；noise reduction efficiency

TB532

A

0493-2137(2015)01-0033-06

10.11784/tdxbz201308055

2013-08-26；

2013-12-03.

科技部国际科技合作资助项目(2007DFB50150-2).

郝志勇（1957— ），男，博士，教授.

郝志勇，haozy@zju.edu.cn.

时间：2014-01-03.

http://www.cnki.net/kcms/doi/10.11784/tdxbz201308055.html.