一种三自由度冗余驱动并联模块的刚度分析
宋轶民,翟学东,孙 涛,董 罡,连宾宾
一种三自由度冗余驱动并联模块的刚度分析
宋轶民,翟学东,孙 涛,董 罡,连宾宾
(天津大学机构理论与装备设计教育部重点实验室,天津 300072)
研究了一种三自由度并联模块的刚度建模方法.该模块采用冗余驱动技术,可满足搅拌摩擦焊作业高刚度、大工作空间/机座体积比要求.分析了该模块的结构组成与工作原理,并应用螺旋理论建立其刚度解析模型,所获广义雅可比矩阵与驱动/约束刚度矩阵物理含义清晰.借助有限元分析验证刚度解析模型的有效性,进而实现全域刚度性能预估,为该模块的刚度优化设计及物理样机开发提供了理论依据.
并联机构;冗余驱动;刚度;螺旋理论;广义雅可比矩阵
搅拌摩擦焊是英国焊接研究所于1991年首创的一种新型固态焊接技术,现已广泛应用于深海钢结构裂纹修复、高压油气管道在线开孔作业中[1].为提供足够的法向压力并相对待焊接对象移动,现有搅拌摩擦焊装备多为龙门式串联构型,其体积庞大,制造成本高[2].
近年来,以Tricept[3]、Exechon等为代表的一类五坐标混联构型装备,因具有刚度高、工作空间/机座体积比大、可重构能力强等优点,受到了学术界与工业界的广泛关注.其中,西班牙PKM公司开发的Tricept 9000型五坐标混联作业单元,已成功应用于搅拌摩擦焊作业[4].
为突破国际专利技术壁垒,黄田等[5]发明了一种新型五坐标混联作业单元——Tricept-IV.该作业单元由一个三自由度并联模块(3-UPS&UPP 机构)与一个二自由度转头(A/C转头)串接而成.研究表明,因采用了冗余驱动技术,该并联模块可获得更大的工作空间/机座体积比[6],且可调节各支链伺服电机功率分配[7].
刚度设计是并/混联构型装备性能设计的重要环节之一.为研制上述具有我国自主知识产权的混联构型搅拌摩擦焊装备,必须深入开展刚度分析/预估技术研究,以便为物理样机详细机械结构设计提供理论依据.
近年来,国内外学者已对并/混联机构的刚度性能进行了深入的研究.Goldsmith[8]应用结构矩阵分析法建立了3-UPU机构的刚度解析模型.Company等[9]借助矢量法和变形叠加原理,研究了一种三坐标并联机床的运动学与刚度设计问题.Tsai等[10]分析了3-RUU等三自由度并联机构的刚度性能,但仅计入了驱动装置的弹性.Zhang等[11]应用螺旋理论,并引入虚设铰链约束,构造出了Tricept机构的刚度解析模型.此外,Wang等[12]借助有限元技术,预估了五自由度混联机器人TriVariant的刚度性能.需要指出的是,上述研究均未涉及冗余驱动并联机构.
考虑到A/C转头的刚度问题相对简单,本文以Tricept-IV作业单元的冗余驱动并联模块为研究对象,应用螺旋理论创建其刚度解析模型,进而预估其全域刚度分布规律,以期为后续的刚度优化设计奠定基础.
1 机构组成及工作原理
如图1所示,该冗余驱动并联模块由静平台、动平台、3条UP S支链和1条UPP,支链组成;U、P、S分别表示虎克铰链、移动副和球铰链,,P,表示主动移动副.机构初始位形时,3条UP S支链关于UPP,支链呈轴对称分布.UPS支链一端通过虎克铰链与静平台相连,另一端通过球铰链与动平台相连.UPP,支链一端通过虎克铰链与静平台相连,中部通过丝杠螺母副与动平台相连,末端则与A/C转头(图1中未示出)固接.
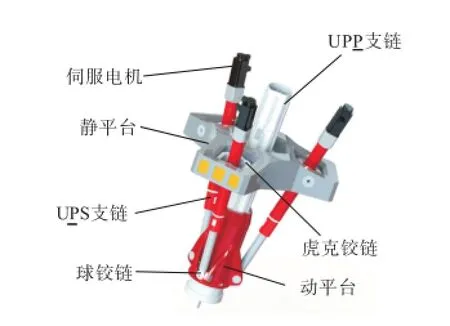
图1 三自由度冗余驱动并联模块虚拟样机Fig.1 Virtual prototype of 3-DOF redundantly actuated parallel module
UP S支链与UPP,支链的机械结构组成分别如图2和图3所示.
该冗余驱动并联模块的机构运动示意如图4所示.其中,点Bi(i=1,2,3)为第i条UPS 支链连架虎克铰链中心,点Ai(i=1,2,3)为第i条UPS支链球铰链中心;点O为UPP,支链连架虎克铰链中心,点A4为UPP,支链经丝杠螺母副与动平台的连接点.定义由点Bi(i=1,2,3)构成的等边三角形为静平台,由点Ai(i=1,2,3,4)构成的正三棱锥为动平台,其底面为等边三角形△A1A2A3.需要指出的是,UPP,支链中两移动副轴线重合且正交于△A1A2A3.

图2 UPS支链的机械结构Fig.2 Structure diagram of UPS limb
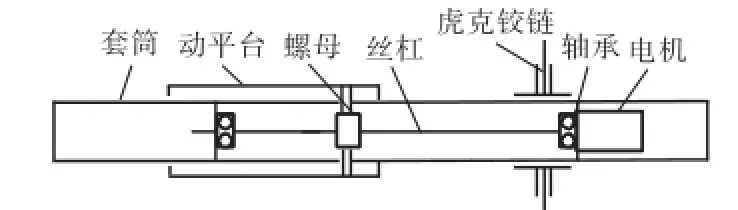
图3 UPP支链的机械结构Fig.3 Structure diagram of UPPlimb

图4 三自由度冗余驱动并联模块机构运动示意Fig.4 chematic diagram of motion of 3-DOF redundantly actuated parallel module
如图4所示,该模块为一球坐标型并联机构,其自由度数目为3.如锁定UPP,支链P,副,该模块将退化为3-UP S&UP机构,通过各UPS支链P,副的相互配合,UPP,支链末端点可到达工作空间内某点A5.之后,如锁定各UPS支链P,副并释放UPP,支链P,副,因螺母与动平台固接(参见图3),UPP,支链将相对动平台移动,其末端点可到达工作空间内另一点A6.如各支链P,副同时驱动,该模块则可实现上述两运动的合成.因此,该冗余驱动模块可实现更大的工作空间[6],并可调节各支链伺服电机的功率分配[7].
为准确描述该模块的运动,建立如图4所示的坐标系.以△B1B2B3中心点O为原点建立固定坐标系O-xyz,其x轴与UPP,支链连架虎克铰链外圈轴线重合,z轴正交于静平台并指向动平台,y轴满足右手定则.分别以点A5、A6为原点建立动坐标系A5x′y′z′和A6x′′y′′z′′,其坐标轴与Oxyz的坐标轴保持瞬时平行.图4中,s1,i和s2,i(i=1,2,3)分别表示第i条UP S支链连架虎克铰链外圈和内圈轴线的单位矢量;qi和s3,i(i=1,2,3)分别表示第i条UP S支链的长度及其轴线单位矢量;s1,4和s2,4分别表示UPP,支链连架虎克铰链外圈和内圈轴线的单位矢量;q4和qp分别表示点O至点A5的距离和点A5至点A6的距离,ai(i=1,2,3)为点A5至点Ai的矢量;s3,4表示UPP,支链轴线的单位矢量.
此外,为构建该模块的刚度解析模型,以点A5为原点建立动坐标系A5uvw,其v轴与UPP,支链连架虎克铰链内圈轴线保持瞬时平行,w轴与UPP,支链轴线保持瞬时平行,u轴满足右手定则.以点A6为原点建立动坐标系A6u′v′w′,其坐标轴与A5uvw的坐标轴保持瞬时平行.
2 广义雅可比矩阵
本文用射线坐标描述运动螺旋,用轴线坐标描述力螺旋[13].
如前所述,如锁定UPP,支链P,副,该模块可等效为3-UPS&UP机构.此时,UPP,支链末端点在坐标系A5x′y′z′下的瞬时运动螺旋$t,A5可表示为



式中:03×1为3行1列零矩阵;ai=Rai′,a′i为点Ai在坐标系A5uvw下的位移矢量;R为坐标系A5uvw相对于坐标系A5x′y′z′的姿态转换矩阵,且

定义$ˆwa,3,i为第i条UPS支链中与其P,副对应的单位驱动力螺旋,$ˆwc,j,4为UPP,支链中与第jc个单位受限
c螺旋对应的单位约束力螺旋.将式(1)两端关于$ˆwa,3,i作内积,得
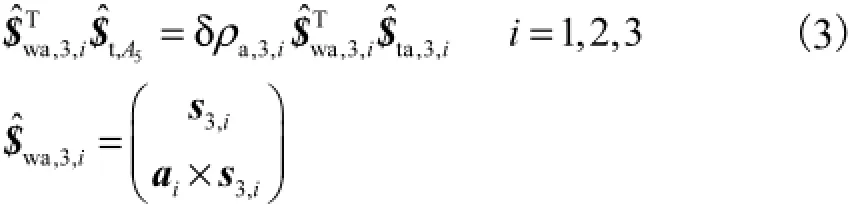
将式(2)两端关于$ˆwc,jc,4作内积,得

当UPP,支链末端点到达点A5时,如锁定各UPS支链P,副并释放UPP,支链P,副,通过丝杠螺母副,UPP,支链末端将沿其轴线相对于动平台移动至点A6.此时,静平台、动平台及3条UP S支链可等效为一新的静平台,而该模块则可等效为一仅能沿UPP支链轴线移动的P,支链.此时,UPP,支链末端点在坐标系A6x′′y′′z′′下的瞬时运动螺旋$t,A6可表示为

式中:$ˆta,1,5、δρa,1,5分别为该等效支链的单位许动螺旋及沿该单位许动螺旋的线变形;$ˆtc,j,5、δρc,j,5分别
cc为该等效支链中第jc(jc=1~5)个单位受限螺旋及沿(绕)该单位受限螺旋的线(角)变形,且
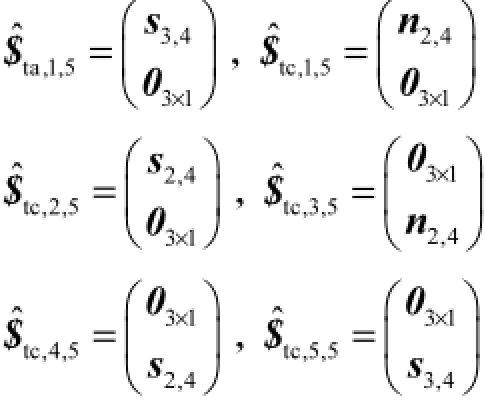
定义$ˆwa,1,5为UPP,支链中与P,副对应的单位驱动力螺旋,将式(5)两端关于$ˆwa,1,5作内积,得

由图4以及点A6相对于点A5的运动,可知

式中:tT为射线坐标描述方法下坐标系5Axyz′′′′′′相对于坐标系6Axyz′′′′′′的66×变换矩阵;Ei为i阶单位矩阵;3,4[]×s为3,4s的反对称矩阵[14].
将式(3)、(4)、(6)及(7)合并,并改写成矩阵形式得

式(8)又可改写为

式中:J、aJ及cJ分别为该冗余驱动并联模块的广义雅可比矩阵及其驱动、约束子雅可比矩阵.
3 刚度解析模型
不失一般性,在构造上述冗余驱动并联模块的刚度解析模型时,视静平台、动平台均为理想刚体,忽略各轴承的接触变形,并假定其余各零部件变形均属线弹性小变形范畴、各铰链所受约束均为理想约束.
由静力学可知,作用于该模块UPP,支链末端的外力螺旋应与各支链提供的驱动力螺旋及约束力螺旋构成一个平衡力系.由图4可知,作用于UPP,支链末端的外力螺旋$w,其一部分由UPP,支链提供的驱动力螺旋和约束力螺旋平衡,而另一部分则需通过丝杠螺母副由3条UPS支链提供的驱动力螺旋平衡.因此,有

式中:fa,3,i、fc,j,4、fa,1,5用以度量$ˆwa,3,i、$ˆwc,j,4及$ˆwa,1,5
c c对$w的贡献;Tw为轴线坐标描述方法下坐标系A5x′y′z′相对于坐标系A6x′′y′′z′′的6×6变换矩阵.
将式(13)、(14)代入式(12),并注意到T=T-T,
wt
可得

根据虎克定律可知,


式中:Ka=diag[ka,i],ka,i(i=1,2,3)为第i条UPS支链沿其轴线方向的等效刚度系数,ka,4为UPP,支链沿其轴线方向的等效刚度系数;Kc=diag[kc,jc,4],kc,jc,4(jc=1,2,3)为UPP,支链中第jc个单位受限螺旋方向的等效刚度系数.
将式(16)、(17)、(9)、(10)代入式(15),得

式中K、Ka及Kc分别为该模块的刚度矩阵、驱动刚度矩阵及约束刚度矩阵.
根据UP S、UPP,支链的机械结构(见图2和图3),可将其抽象为串联弹簧系统[15],并获得其刚度系数分别为

式中:ka,i,m(m=1,2,…,7)分别表示第i条UP S支链中球铰链、伸缩杆、螺母、丝杠、轴承、套筒及虎克铰链沿该支链轴向的刚度系数;ka,4,m(m=1,2,…,5)分别表示UPP,支链中套筒、螺母、丝杠、轴承及虎克铰链沿该支链轴向的刚度系数.
需要指出的是,式(17)中,kc,2,4为UPP,支链沿其连架虎克铰链内圈轴线s2,4方向的等效刚度系数,物理含义明确;而由kc,1,4和kc,3,4分别表示的UPP,支链绕n1,4方向和沿n2,4方向的等效刚度系数,其物理含义并不明确,难以获得解析表达式.由该模块机械结构特点可知,UP S支链只提供驱动而不提供约束,UPP,支链既提供驱动又提供约束;即当UPP,支链末端受到外力螺旋作用时,UPS支链只提供沿其支链轴线方向的驱动力螺旋而不提供约束力螺旋,而UPP,支链则需提供1个驱动力螺旋、2个约束力螺旋及1个约束力偶螺旋.
为获得约束刚度矩阵的具体表达,在坐标系A6x′′y′′z′′下,可将UPP支链的受限螺旋用另一组单位受限螺旋表示,即

式中:$ˆtc,1和$ˆtc,2分别表示UPP,支链末端沿n2,4和s2,4的单位挠度;$ˆtc,3和$ˆtc,4分别表示UPP,支链末端绕n2,4和s2,4的单位转角;$ˆtc,5表示UPP,支链末端绕s3,4的单位扭角.
同理,在坐标系A6x′′y′′z′′下,将UPP,支链所产生的约束力螺旋用另一组单位力螺旋表示,即

式中:$ˆwc,1和$ˆwc,2分别表示UPP支,链末端沿n2,4和s2,4方向的单位剪力;$ˆwc,3和$ˆwc,4分别表示UPP,支链末端绕n2,4和s2,4方向的单位弯矩;$ˆwc,5表示UPP,支链末端绕s3,4方向的单位扭矩.
因此,式(2)可改写为

式中δρa,ja,4和δρc,mc(mc=1,2,…,5)分别为沿(绕)轴线的线(角)变形.
因UPP,支链末端绕$ˆtc,3和$ˆtc,4轴线的角变形δρc,3和δρc,4与沿$ˆtc,1和$ˆtc,2轴线的线变形δρc,1和δρc,2耦合,根据变形协调条件,可将δρc,3和δρc,4用δρc,1和δρc,2表示[12],有

将式(21)两端关于$ˆwc,k,4(kc=1,2,3)做内积,并
c与式(7)、(22)联立,可得[16]

同理,在坐标系A6x′′y′′z′′下,UPP,支链的约束力螺旋Tw$wc可用一组单位螺旋(kc=1,2,3)表示,也可用上述定义的另一组单位螺旋(mc=1,2,…,5)线性表示,即

式中fc,m(mc=1,2,…,5)用以度量$ˆwc,m对$wc的
cc贡献.
注意到式(21)两端表示同一力螺旋,在相同的受限螺旋上做功相等.对式(21)两端关于$t,A6作内积,并将式(19)代入其中,即可建立fc,kc,4和fc,mc间的映射关系,即
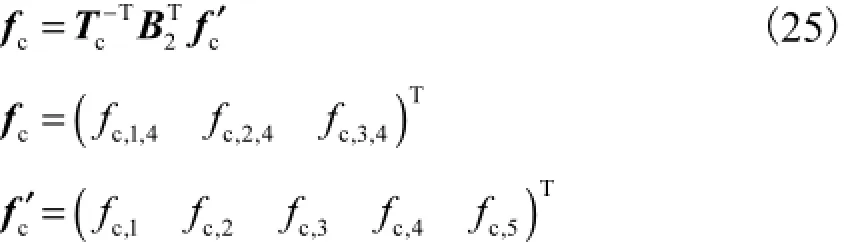
由虎克定律知

式中:Ke为UPP,支链超单元的4×4界面弯曲刚度矩阵[12];kα为UPP,支链末端绕轴线s3,4的扭转刚度系数,且

式中kα,i(i=1,2,3)依次表示UPP,支链套筒前段、套筒后段及连架虎克铰链绕该支链轴线的扭转刚度系数(见图3).
将式(23)、(26)代入式(25),得

将式(27)两端左乘JT,并代入式(15),可得
c

由此,可得该冗余驱动并联模块的约束刚度矩阵Kc的具体表达式.
4 全域刚度预估
为方便全域刚度预估及后续刚度优化设计,将坐标系A6x′y′z′下描述的刚度矩阵K转换至坐标系A6uvw下,可得该并联模块的整机刚度矩阵Ks为

不失一般性,给定该模块的工作空间为一半径R=400mm、高h=300mm的圆柱体,如图5所示.
当锁定UPP,支链P,副时,该模块工作空间为一半径400,mm、高100,mm的圆柱体.当释放UPP,支链P,副时,UPP,支链末端又可伸长h2=200,mm.借助该模块的虚拟样机模型(见图1),针对工作空间中的典型位姿(见图5),利用商用软件建立其有限元模型并求解模块末端的各向刚度.位姿Ⅰ处,各UPS支链呈轴对称分布,UPP,支链P,副伸长量达到最大值(200,mm);位姿Ⅱ处,其UPP,支链P,副伸长量亦达到最大值,而此时模块末端位于工作空间的边缘处.

图5 工作空间典型位姿Fig.5 Typical positions in the workspace
上述典型位姿处,刚度解析模型和有限元模型的计算结果如表1所示.

表1 刚度解析模型与有限元模型计算结果对比Tab.1 Comparison between analytical and FEA numerical results of stiffness models
在未计入静、动平台弹性和忽略轴承接触变形的前提下,解析模型和有限元模型的计算误差小于15%.因此,上述刚度解析模型是有效的,可用以预估该模块的全域刚度分布.
根据各零部件刚度,由解析模型可求得坐标系A6uvw下,该模块末端A6(x,y,z)在其工作空间上(z=1400mm)、中(z=1500mm)、下(z=1700mm)平面上的各向刚度分布情况.图6中,klu、klv、klw分别表示沿u、v及w轴的线刚度;kau、kav、kaw分别表示绕u、v及w轴的角刚度.由图6可知:
(1) 当末端z坐标一定时,各向刚度分布均关于x、y轴对称;
(2) 当末端z坐标一定时,随着(x2+y2)增大,各向刚度单调递减;
(3) 当末端22()xy+一定时,随着z坐标增大,各向刚度单调递减.
此外,由表1及图6可知:各向线刚度中,klw最大,klu与klv接近;各向角刚度中,kau、kav接近,kaw最小.
上述线(角)刚度分布特征与该冗余驱动模块中各支链、铰链布置方式有关,且符合材料力学常识,进一步验证了刚度解析模型的有效性.

图6 三自由度冗余驱动并联模块各向刚度分布Fig.6 Stiffness distribution of 3-DOF redundantly actuated parallel module
5 结 论
(1) 以新型五坐标混联构型装备Tricept-IV的冗余驱动并联模块为研究对象,借助螺旋理论构建了该模块的静刚度半解析模型,所推导的广义雅可比矩阵及驱动/约束刚度矩阵具有清晰的物理含义.
(2) 典型位姿处有限元分析及全域刚度预估结果表明,所建立的静刚度解析模型有效,可用以指导该模块的刚度优化设计及物理样机开发.
[1] Nandan R,DebRoy T,Bhadeshia H. Recent advances in friction-stir welding-process,weldment structure and properties[J]. Progress in Materials Science,2008,53(6):980-1023.
[2] 栾国红. 搅拌摩擦焊在中国的发展[J]. 电焊机,2004(增l):98-106.
Luan Guohong. Development of friction stir welding in China[J]. Electric Welding Machine,2004(Suppl l):98-106(in Chinese).
[3] Neumann K E. Robot:US,4732525A[P]. 1988-03-22.
[4] Production Description of Tricept 9000 of PKM[EB/OL]. http://www. pkmtricept. com,2013-09-22.
[5] 黄 田,刘海涛,赵学满,等. 含冗余自由度的多坐标混联机器人:CN,1739926A[P]. 2006-03-01.
Huang Tian,Liu Haitao,Zhao Xueman,et al. Multi-Coordinate Hybrid Robot Containing Redundant Freedom:CN,1739926A[P]. 2006-03-01(in Chinese).
[6] Sun Tao,Song Yimin,Li Yonggang,et al. Workspace decomposition based dimensional synthesis of a novel hybrid reconfigurable robot[J]. ASME Trans Journal of Mechanisms and Robotics,2010,2(3):031009-1-031009-8.
[7] 洪 锐. Tricept-IV混联机器人控制系统开发[D]. 天津:天津大学机械工程学院,2009.
Hong Rui. Development of Control System for the Hybrid Robot Tricept-IV[D]. Tianjin:School of Mechanical Engineering,Tianjin University,2009(in Chinese).
[8] Goldsmith P B. Design and kinematics of a three-legged parallel manipulator[J]. IEEE Transactions on Robotics and Automation,2003,19(4):726-731.
[9] Company O,Pierrot F. Modeling and design issues of a 3-axis parallel machine tool[J]. Mechanism and Machine Theory,2002,37(11):1325-1345.
[10] Tsai L W,Joshi S. Kinematic analysis of 3-DOF position mechanisms for use in hybrid kinematic machines[J]. ASME Trans Journal of Mechanical Design,2002,124(2):245-253.
[11] Zhang D,Wang Lihui. Conceptual development of an enhanced tripod mechanism for machine tool[J]. Robotics and Computer-Integrated Manufacturing,2005,21(4/5):318-327.
[12] Wang Y Y,Huang T,Zhao X M,et al. Finite element analysis and comparison of two hybrid robots-the Tricept and the Trivariant[C]// Proceedings of the IEEE/ RSJ International Conference on Intelligent Robots and Systems. Beijing,China,2006:490-495.
[13] Hunt K H. Kinematic Geometry of Mechanisms[M]. Oxford:Oxford University Press,1978.
[14] Huang T,Liu H T,Chetwynd D G. Generalized Jacobian analysis of lower mobility manipulators[J]. Mechanism and Machine Theory,2011,46(6):831-844.
[15] 孙 涛,宋轶民,李永刚,等. 一类四自由度混联可重构主模块的全域静刚度预估[J]. 天津大学学报,2010,43(11):1003-1008.
Sun Tao,Song Yimin,Li Yonggang,et al. Global stiffness estimation of 4-DOF hybrid and reconfigurable module[J]. Journal of Tianjin University,2010,43 (11):1003-1008(in Chinese).
[16] 刘海涛. 少自由度机器人机构一体化建模理论、方法及工程应用[D]. 天津:天津大学机械工程学院,2010.
Liu Haitao. Unified Parameter Modeling of Lower Mobility Robotic Manipulators:Theory,Methodology and Application[D]. Tianjin:School of Mechanical Engineering,Tianjin University,2010(in Chinese).
(责任编辑:金顺爱)
Stiffness Analysis of a 3-DOF Redundantly Actuated Parallel Module
Song Yimin,Zhai Xuedong,Sun Tao,Dong Gang,Lian Binbin
(Key Laboratory of Mechanism Theory and Equipment Design of Ministry of Education,Tianjin University,Tianjin 300072,China)
Stiffness modeling method of a 3-degree-of-freedom(3-DOF)parallel module was studied. The redundant joint of the module could meet the requirements of the friction-stir welding for high stiffness and large ratio of workspace to base. The topology structure and working mechanism of the module were analyzed and the stiffness model of the parallel module was established based on screw theory,whose Jacobian matrices of actuations and constraints were of clear physical implication. Effectiveness of the stiffness model was validated using finite element method and stiffness evaluation of the whole workspace was achieved,which provides theoretical foundation for optimal stiffness design and physical prototype development of the redundantly actuated parallel module.
parallel mechanism;redundantly actuated;stiffness;screw theory;generalized Jacobian matrix
TP241.2
A
0493-2137(2015)01-0025-08
10.11784/tdxbz201309083
2013-09-23;
2013-10-29.
国家自然科学基金资助项目(51475321,51075295,51205278);高等学校博士学科点专项科研基金资助项目(2012003211003,2012003212003);天津市应用基础与前沿技术研究计划资助项目(11JCZDJC22700,13JCQNJC04600).
宋轶民(1971— ),男,博士,教授,ymsong@tju.edu.cn.
孙 涛,stao@tju.edu.cn.
时间:2014-01-03.
http://www.cnki.net/kcms/doi/10.11784/tdxbz201309083.html.

