粉煤灰预处理浆液槽停车与启动瞬态过程研究
刘丽艳,李晨辰,朱国瑞,张战军,孙俊民,谭 蔚
粉煤灰预处理浆液槽停车与启动瞬态过程研究
刘丽艳1,李晨辰1,朱国瑞1,张战军2,孙俊民2,谭 蔚1
(1. 天津大学化工学院,天津 300072;2. 大唐国际再生资源开发有限公司,呼和浩特 010206)
用数值模拟方法对粉煤灰预处理浆液槽内固相颗粒的沉降及悬浮瞬态过程进行研究,同时以稳态模拟结果为初值对工业实际生产中的突发停车事故进行了研究,并分析了颗粒相分布和搅拌功率在停车以及再启动过程中的变化情况.结果表明,在浆液槽停车过程中内部固液两相运动速度不断衰减,固相颗粒逐渐在槽底形成沉积层,槽上部出现清液层;再启动之后固相颗粒重新分布于浆液槽中,停车0.5,h和1.0,h分别需经过6,min和10,min的搅拌才可以再次达到均匀悬浮状态,而且再启动初期搅拌功率陡增,最高可以达到稳定水平的1.6倍,如果不在搅拌设备上预先加装辅助搅拌设备则会有烧毁电机的危险.本研究可以有效预防突发停车事故.
浆液槽;两相流;数值模拟;停车;再启动
预脱硅是高铝粉煤灰提取氧化铝工艺的第一步,而粉煤灰预处理浆液槽位于整条工艺线最前端,通过搅拌实现粉煤灰和氢氧化钠溶液预混、细化颗粒的目的.在预混及细化过程中固相的均匀分布可以使粉煤灰充分反应,避免对下游反应造成影响[1].
目前对于单相流搅拌的模拟研究已经比较充分,涵盖了牛顿流体以及非牛顿流体领域[2],而固液悬浮操作涉及到多相流搅拌流场的数值模拟[3],相对比较复杂,也一直是相关学术领域的研究重点,针对不同的搅拌目的以及流场特点,学术界的研究关注点也不尽相同.目前针对固-液两相流的数值模拟研究涉及到湍流模型选择[4]以及相间曳力模型的优化[5]、搅拌器的功率曲线[6]、固体颗粒完全离底悬浮转速[7-8]、单层以及多层桨在低浓度固含情况下颗粒的分散特性[9]、颗粒浓度分布以及混合过程等方面[10-11].这些重点研究方向都已经取得了明显的进展,所研究的搅拌器与搅拌槽类别也是多种多样[12],并且考虑了搅拌桨的优化设计[13].但是,由于实际工业中的大型搅拌槽观测采集数据非常困难,无法时时了解槽内的流场情况,小试实验操作也需考虑一系列复杂的放大准则,未必会很好地放大展现实际运行工况,因此工业生产中大型搅拌槽的模拟研究以及优化设计一直都是研究的重点和难点[14].
在研究正常操作工况的基础上进一步分析停车对搅拌设备造成的影响非常必要,工厂在实际运行过程中一旦遭遇停车事故,浆液槽内流场的固液分布情况将会发生显著变化,流场将经历降速以及固相颗粒沉积过程,下层叶轮也可能被固体颗粒堆埋,再启动时瞬间功率过大有烧毁电机的危险.当堆埋严重时搅拌桨将无法再次启动,通常要用液体或压缩空气喷枪使叶轮周围物料松动后才能启动.对于高浓度淤浆液且固体密度较大的场合有必要在搅拌设备上预先安装再启动的辅助装置,搅拌设备合理的设计以及正确的操作方法是保证设备寿命的关键.停车事故亦会对排出的产品质量造成影响,这就需要对停车时间以及再启动过程进行研究[15].但是目前现有研究表明停车以及再启动瞬时过程沉降效果不明显而且缺乏实验的验证,为此,笔者对浆液槽停车及再启动瞬时过程进行研究,深入分析停车事故.首先对浆液槽已经搅拌均匀的稳态流场进行研究,进一步应用瞬态解算器对停车及再启动这一类突发状况进行分析,重点考虑流场分布以及再启动过程中的功率变化情况,提出可行性建议来预防停车事故对产品质量以及电机和桨叶所造成的危害.
1 数值模拟
1.1 模型建立
根据实际搅拌装置建立模型,其尺寸如表1所示,采用双层三叶CBY搅拌桨,槽内均布3块挡板,装填系数为0.85,建模时忽略桨叶以及挡板厚度.采用Gambit 2.3.16划分网格,桨叶以及挡板等重点区域表面采用尺寸较小、质量较高的面网格,搅拌桨周围流场(旋转域)采用尺寸较大的四面体非结构网格,流场其余部位进一步加大四面体网格的尺寸.经过网格无关性验证之后,选取计算较快的网格方案,网格数为1,616,402.图1为模型的网格示意.

表1 浆液槽验证模型结构尺寸Tab.1Size and structure of verification model of slurry tank m

图1 浆液槽模型网格Fig.1 Mesh of slurry tank model
1.2 物性参数
本文模拟的固液悬浮浆液成分为粉煤灰和氢氧化钠溶液,主要物性参数如表2所示,颗粒粒径取体积平均粒径60,μm(根据工厂物料测试所得).

表2 悬浮液物性参数Tab.2 Physical parameters of slurry
1.3 数值方法及研究内容
粉煤灰-氢氧化钠浆液槽内为固-液两相,模拟计算中采用欧拉-欧拉多相流模型,该方法适用于较多气泡或较大气量的气液两相流以及较多固体颗粒的液固两相流.两种流体运动规律服从各自的控制微分方程组,可表示为
相体积分率守恒方程

两相连续性方程

两相动量方程

式中:下标l表示液相;下标s表示固相;α 为相含率;Msl为两相动量传递源相,由相间作用力、虚拟质量力和升力3项组成.虚拟质量力是由于固体颗粒的加速运动而施于周围液体的力,它的加入与否对计算结果影响不大.相间作用力对两相流中的固体颗粒运动影响最为显著,且有

固-液相间作用力Rsl与动量传递系数的关系为

固-液相间传递交换系数Ksl采用颗粒间碰撞的Gidaspow模型,即

曳力函数CD为
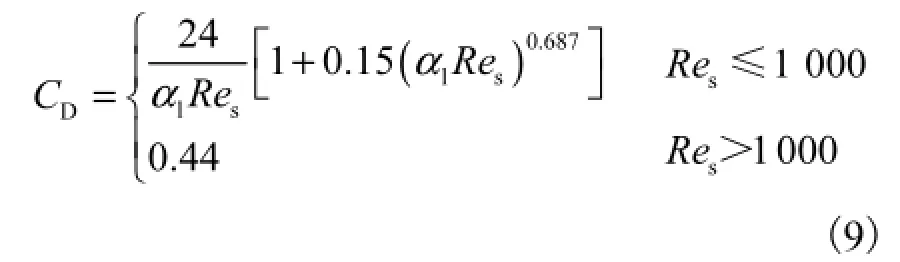
使用Ansys FLUENT 14.0对浆液槽不同停车和再启动时间下的流场进行模拟研究,并对再启动初期的搅拌功率进行计算.
1.4 边界条件及求解方法
静壁面包括浆液槽壁面、底面以及挡板,动壁面包括搅拌桨叶表面和搅拌轴表面.动静壁面对液相均设置为无滑移壁面;对颗粒相设置为自由滑移壁面,且设定不同的反射系数以及壁面恢复系数.搅拌液面设置为自由液面,采用MRF方法进行计算,桨叶所在区域的参考系是以桨叶速度旋转,其他区域使用静止参考系,用来计算叶轮区以外的流动场,2个区域交界面定义为interface.
采用有限体积法对浆液槽流场进行离散,使用RNG k-ε模型进行模拟,近壁区采用标准壁面函数,对流项采用Quick迎风格式进行离散,与一阶离散格式相比,Quick离散格式计算精度有很大的提高,压力速度耦合采用SIMPLE算法,各参数的计算残差收敛在1×10-3以内.本文所研究搅拌体系不考虑入口和出口,因此只对固液两相在整体流场域的情况进行初始化,设定初始时刻固液两相在槽内均匀分布,进行稳态流场模拟,待流场中固液两相分布不再发生变化时认为流场已经稳定,选取此时的结果作为初值采用非稳态解算器模拟浆液槽停车及再启动过程,以0.1,s时间步长进行迭代,在内存为96G的惠普Z800工作站上进行计算.
2 沉降实验
为获得停车过程中固相颗粒的沉积速率参数进行沉降实验.沉降实验在2,000,mL的烧杯中进行,外径130,mm,高度195,mm.烧杯外侧贴上分度值1,mm的标尺,倒入110,mm高度粉煤灰浆液,搅拌均匀同时开始计时,读取上层清液厚度随时间的变化情况,进一步计算得出清液层厚度的增加速率.
3 结果分析与讨论
3.1 实验验证
球形颗粒的堆积有最大堆积与最小堆积体积之分,最小堆积体积通过计算为0.52,表明当局部颗粒浓度高于此堆积体积时颗粒即没有完全悬浮起来,在局部发生堆积,如果堆积进一步加剧,则颗粒浓度会逐渐增加逼近最大堆积体积,当搅拌槽内颗粒最大浓度也小于最小堆积体积时,全槽颗粒达到完全离底悬浮状态.停车过程中粉煤灰-氢氧化钠浆液槽底部颗粒堆积层厚度以及上层清液厚度变化的模拟结果如图2和图3所示.浆液槽在发生停车事故后,固相颗粒逐渐沉积,停车400,s后最先在槽底中央搅拌轴周围区域发生颗粒的堆积,随着停车时间的增加,颗粒堆积层逐渐加厚,而且颗粒堆积越来越密实,接近最大堆积,停车1,h之后颗粒堆积层已经达到0.54,m;同样,在停车过程中浆液槽上部会出现基本不含颗粒相的清液层,停车30,s后清液层逐渐加厚,1,h后清液层的厚度已经接近槽体高度的一半.

图2 停车过程中颗粒堆积厚度变化情况Fig.2Variation of thickness of particle accumulation in stop process
通过图3可得清液层厚度的增加速率为7.43×10-4,m/s(以下均指匀速段的速率),通过沉降实验得到该悬浮浆液清液层厚度的增加速率为7.00×10-4m/s,与数值模拟得到的结果非常接近,二者相对误差为6.14%,在工程计算允许的范围之内,可以证明本文模拟在定量和定性上的有效性.

图3 停车过程中上层清液厚度变化情况Fig.3 Variation of thickness of supernatant liquid in stop process
3.2 固相颗粒分布
由于无法观测到工业实际运行中浆液槽内部流场的变化情况,因此只能采用数值模拟的方法进行研究.图4为停车过程中流场内某一纵切面的固含率分布情况,在正常操作工况下,浆液槽内固液两相分布较均匀,当遭遇停车事故时,固相颗粒逐渐沉积到槽底部,再次启动时颗粒相将会重新分布于浆液槽中,经过一定时间的搅拌再次达到均匀悬浮的状态,本文所研究的固液两相在36,r/min时刚好可以达到均匀悬浮状态,因此再启动转速均设定为36,r/min.图5和图6分别为停车0.5,h和1.0,h之后再启动时流场中颗粒相的分布情况,可以看到停车0.5,h和1.0,h再启动时分别需经过6,min及10,min的搅拌才可使浆液槽内固液两相基本达到停车前均匀悬浮的状态.由此可见,在完全沉降之前停车时间的延长势必会对再启动过程造成更为不利的影响,不但达到稳定状态的时间增加,而且稳定流场也会消耗更多的能耗.
图7和图8分别为图4~图6所研究纵切面内停车0.5,h、1.0,h及再启动过程固含率分布标准差的变化情况.固含率分布标准差是指某个截面上根据网格密度,对每个截面网格内的颗粒相体积分数与整个截面的平均值做标准差计算,得到的结果可以更为直观科学地体现某一截面上颗粒分布的均匀程度.从图中可以看到在停车时间内标准差不断升高,表明在此时间段内颗粒分布越来越不均匀,出现上层清液区以及底部颗粒堆积区.当搅拌桨再次启动时,固相颗粒分布的标准差不断下降,停车0.5,h之后再启动时需要经过6,min的搅拌才能使浆液槽内的固液两相基本发展到停车前的悬浮状态,而停车1.0,h则需要经过10,min的搅拌.相比于图2~图4中某几个时刻的固含分布而言,图7和图8可以动态反映浆液槽中固液两相每时每刻的混合情况,能够达到实时监控的效果.由于随着停车时间的延长,颗粒沉积会不断加剧,再启动过程的隐患随之增大,而且达到稳定水平需要更多的能耗,因此在实际生产中对于停车事故的时间应严格把控.

图4 停车过程中固相颗粒分布情况Fig.4 Distribution of solid concentration in stop process
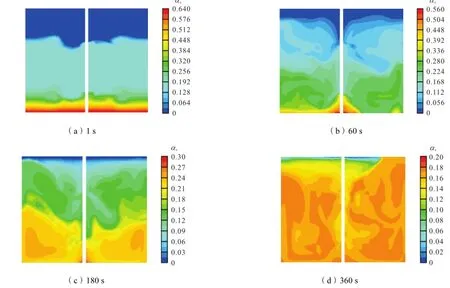
图5 停车0.5,h再启动过程中固相颗粒分布情况Fig.5 Distribution of solid concentration in restart process after stopping for half an hour

图6 停车1.0,h再启动过程中固相颗粒分布情况Fig.6 Distribution of solid concentration in restart process after stopping for one hour
3.3 搅拌功率
发生停车后的一段时间内搅拌功率为负值,这是由于流体的惯性使得流体速度不会瞬时减小到零,而是一个逐渐衰减的过程,在此期间流体会对搅拌桨做功,当流体速度趋近于零之后,搅拌功率将会稳定在零附近,这期间对电机不会造成任何风险.停车事故的危害存在于再启动过程,由于下层桨局部固含率的增多以及流场趋近于静止状态,因此在再启动初期桨叶要克服自身和所推动液体的惯性以及液体的摩擦力,这时桨叶与液体的相对速度最大,因此瞬时的搅拌功率将陡增,电机以及桨叶都会有损毁的危险,搅拌功率值均经历一个先降低后稳定的过程.停车0.5,h和1.0,h再启动过程搅拌功率的变化情况分别如图9和图10所示,P=2,πnT(其中n为搅拌转速,T为转矩,由模拟得到),再启动初期的搅拌功率最高可以达到稳定水平的1.6倍,经过30,s的搅拌混合之后功率值趋于稳定,而且随着停车时间的增加下桨周围固相颗粒会不断增多,启动功率亦会有所增大,从图中可以看到停车1.0,h的启动功率比停车0.5,h的启动功率增加0.3,kW,对电机及桨叶的危害程度更大.在实际工业生产中如果遭遇停车事故,当颗粒沉积堆埋严重时搅拌桨将无法再次启动,通常要用液体或压缩空气喷枪使叶轮周围物料松动后才能启动,对于高浓度淤浆液且固体密度较大容易发生沉降的场合,有必要在搅拌设备上预先安装再启动的辅助装置.
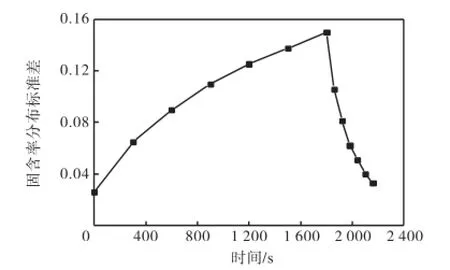
图7 停车0.5,h及再启动过程中固含率分布标准差变化情况Fig.7 Variation of solid concentration distribution standard deviation in stop-for-half-an-hour and restart process
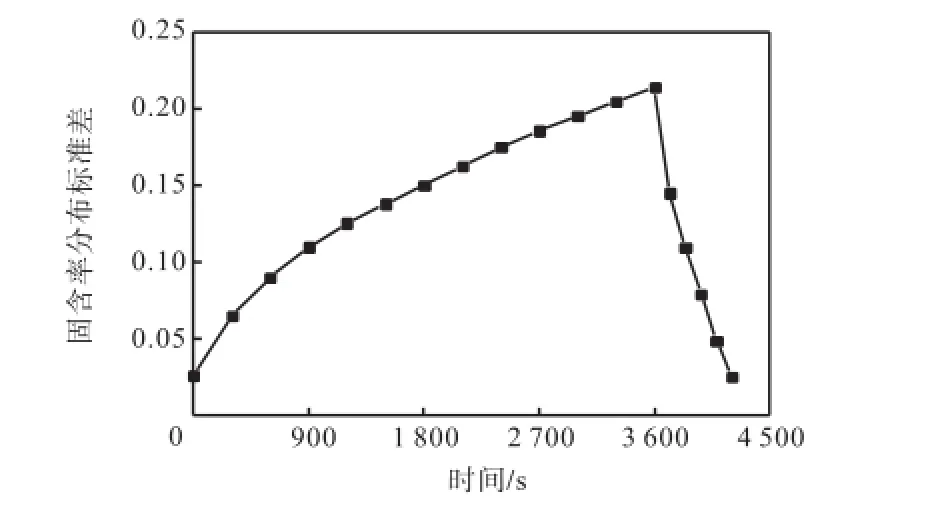
图8 停车1.0,h及再启动过程中固含率分布标准差变化情况Fig.8 Variation of solid concentration distribution standard deviation in stop-for-one-hour and restart process
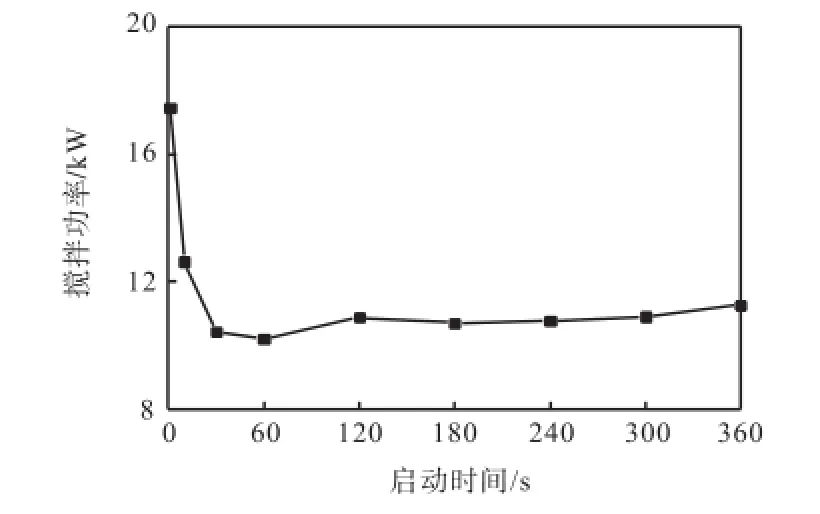
图9 停车0.5,h再启动过程搅拌功率分布Fig.9 Stirring power curve in restart process after stopping for half an hour

图10 停车1.0,h再启动过程搅拌功率分布Fig.10 Stirring power curve in restart process after stopping for one hour
4 结 论
本文采用数值模拟方法对粉煤灰-氢氧化钠浆液槽内固液两相的搅拌混合进行了研究,在稳态模拟结果的基础上对非稳态停车及再启动过程进行了探讨,得到如下结论.
(1) 突发停车事故之后搅拌槽内流体速度不断减小,颗粒逐渐沉积到槽底部,随着停车时间的增加,颗粒堆积层以及清液层逐渐加厚.沉降实验和数值模拟得到的清液层增加速率的相对误差为6.14%,可以证实模拟准确有效,通过本文提出的数据可以为工业实际操作提供理论指导.
(2) 沉降时间对再启动过程有明显影响,停车0.5,h和1.0,h之后再启动时分别需要经过6,min及10,min的搅拌才能使浆液槽内的固液两相基本发展到停车前的悬浮状态.
(3) 再启动时由于下桨局部固含颗粒过多以及整个流场趋于静止状态,导致启动瞬时功率陡增,对电机以及搅拌桨都会造成危害,再启动初期的搅拌功率可以达到稳定水平的1.6倍,而且随着停车时间的延长启动功率会略微增大,对电机以及桨叶造成的隐患加大,因此很有必要为搅拌槽加装辅助搅拌设备.
[1] 张占军. 从高铝粉煤灰中提取氧化铝等有用资源的研究[D]. 西安:西北大学地质系,2007.
Zhang Zhanjun. Research on Extraction of Alumina and Other Useful Resources from High Aluminium Fly Ash [D]. Xi′an:Department of Geology,Northwest University,2007(in Chinese).
[2] 张敏革,张吕鸿,姜 斌,等. 双螺带-螺杆搅拌桨在不同流体中的搅拌流场特性[J]. 天津大学学报,2009,42(10):884-890.
Zhang Minge,Zhang Lühong,Jiang Bin,et al. Performance of flow field in different fluids stirred with double helical ribbon and screw impeller [J]. Journal of Tianjin University,2009,42(10):884-890(in Chinese).
[3] Klenov O P,Noskov A S. Solid dispersion in the slurry reactor with multiple impellers[J]. Chemical Engineering Journal,2011,176/177:75-82.
[4] Fan L,Mao Z,Wang Y. Numerical simulation of turbulent solid-liquid two-phase flow and orientation of slender particles in a stirred tank[J]. Chemical Engineering Science,2005,60(24):7045-7056.
[5] Brucato A,Grisafi F,Montante G. Particle drag coefficients in turbulent fluids[J]. Chemical Engineering Science,1998,53(18):3295-3314.
[6] 永田进治. 混合原理及应用[M]. 马继舜,等译. 北京:化学工业出版社,1984.
Nagata Shinji. Principle and Application of Mixing[M]. Ma Jishun,et al Trans. Beijing:Chemical Industry Press,1984(in Chinese).
[7] Zwietering T N. Suspending of solid particles in liquid by agitators[J]. Chemical Engineering Science,1958,8(3):244-253.
[8] 王振松. 高浓度固-液搅拌槽内流场研究[D]. 北京:北京化工大学化工学院,2005.
Wang Zhensong. The Study of Local Velocities in a Solid-Liquid Stirred Tank with a High Concentration of Solid[D]. Beijing:College of Chemical Engineering,Beijing University of Chemical Technology,2005(in Chinese).
[9] Micale G,Montante G,Grisafi F,et al. CFD simulation of particle distribution in stirred vessels[J]. Chemical Engineering Research and Design,2000,78(3):435-444.
[10] Wang Feng,Wang Weijing,Mao Zaisha. Numerical study of solid-liquid two-phase flow in stirred tanks with Rushton impeller[J]. Chinese Journal of Chemical Engineering,2004,12(5):599-609.
[11] 张国娟,闵 健,高正明,等. 翼形桨搅拌槽内混合过程的数值模拟[J]. 高校化学工程学报,2005,19(2):169-174.
Zhang Guojuan,Min Jian,Gao Zhengming,et al. Numerical simulation of mixing process in a stirred tank with hydrofoil impeller[J]. Journal of Chemical Engineering of Chinese Universities,2005,19(2):169-174(in Chinese).
[12] 杨锋苓,周慎杰,张翠勋,等. 偏心搅拌槽固液悬浮特性[J]. 过程工程学报,2008,8(6):1064-1068.
Yang Fengling,Zhou Shenjie,Zhang Cuixun,et al. Investigation on solid-liquid suspension performance in an eccentrically stirred tank[J]. The Chinese Journal of Process Engineering,2008,8(6):1064-1068(in Chinese).
[13] Zhang Qinghua,Mao Zaisha,Yang Chao,et al. Numerical simulation of barium sulfate precipitation process in a continuous stirred tank with multiple-time-scale turbulent mixer model[J]. Industrial & Engineering Chemistry Research,2008,48(1):424-429.
[14] 陈俊英,李红伟. 化工行业常用搅拌器研究热点[J].现代化工,2011,31(10):12-16.
Chen Junying,Li Hongwei. Study on the research hotspots of mixer in chemical industry[J]. Modern Chemical Industry,2011,31(10):12-16(in Chinese).
[15] 刘 潇,谭 蔚,逄 翀,等. 对大型液-固两相搅拌槽事故停车及再启动过程的数值模拟研究[J]. 高校化学工程学报,2012,26(6):946-951.
Liu Xiao,Tan Wei,Pang Chong,et al. Numerical simulation on the processes of accident power cut and the restart of a large-scale solid-liquid two-phase stirred tank[J]. Journal of Chemical Engineering of Chinese Universities,2012,26(6):946-951(in Chinese).
(责任编辑:田 军)
Transient Numerical Simulation of the Stop and Restart Process in Fly Ash-Sodium Hydroxide Slurry Tank
Liu Liyan1,Li Chenchen1,Zhu Guorui1,Zhang Zhanjun2,Sun Junmin2,Tan Wei1
(1. School of Chemical Engineering and Technology,Tianjin University,Tianjin 300072,China;2. Datang International Recycling Resource Development Company Limited,Hohhot 010206,China)
Numerical simulation method was adopted to study the suspension process of solid particles in the fly ashsodium hydroxide slurry tank.With the steady state simulation results as the initial value of stop of industrial production,the transient solver was applied to analyzing the changes of particle distribution and stirring power during the stop and restart process. The results indicate that,during the stop process,the velocity of the particles and liquid decreases continuously,and solid particles gradually accumulate at the bottom of the tank to form deposition layer,while the upper area of supernatant layer is substantially free of particles. After restarting,the solid particles redistribute in the slurry tank. 6 and 10 minutes of stirring are needed to achieve uniform suspension after stopping for 0.5,h and 1.0,h respectively. There is a steep increase in stirring power at the initial stage of restart process,with the maximum up to 1.6 times that at the stable level.There also exists a risk of burning motor if no auxiliary mixing equipment is preinstalled. This study can offer an effective preventive measure against the damage of sudden stop accidents.
slurry tank;two-phase flow;numerical simulation;stop;restart
TQ027.2;TQ019
A
0493-2137(2015)05-0388-07
10.11784/tdxbz201402003
2014-02-10;
2014-03-12.
国家自然科学基金资助项目(21376167);国家“十一五”科技支撑计划资助项目(2009BAB49B00).
刘丽艳(1977— ),女,博士,副教授,liuliyan@tju.edu.cn.
谭 蔚,wtan@tju.edu.cn.
时间:2014-03-25. 网络出版地址:http://www.cnki.net/kcms/doi/10.11784/tdxbz201402003.html.

