问题串与解法串个性化结构设计的思考

●陈朝阳 (余杭区教育局教研室 浙江杭州 311100)

问题串与解法串个性化结构设计的思考

●陈朝阳 (余杭区教育局教研室 浙江杭州 311100)

针对不同思维层次的学生实施不同的教育是基础教育改革的目标之一.在数学教育中，由于数学教育的特殊性，个性化教育更显得必要.同一个数学问题可以有不同层次的求解思维，设计出不同层次的问题串或解法串，帮助不同认知水平的学生从中理解问题的本质，这是个性化教育的落脚点.数学学习最重要的是数学思维与数学思想的学习，而数学问题求解正是训练学生数学思维的大好时机，因此可以设计个性化的问题串或解法串以训练不同的数学思维.于是，在数学问题串设计中要特别关注个性化结构问题.

1 形象思维型

数学中的形象思维是借助于图形、实物、图像来思考抽象数学概念的一种思维描述，以形助数，直观描述，帮助人们更加容易地理解抽象概念的一种途径.在数学解题中，常用这种思维寻找解题的突破口，解决较难的问题.数形结合思想的基础就是形象思维，在数学教学中培养学生的形象思维是十分重要的.

对于形象思维能力较强的学习者，多用直观或图像的方式来表达求解思维过程，形成问题串或解法串，比如平面向量中“共线定理”是一个重要的知识点，可设计如下的问题串:

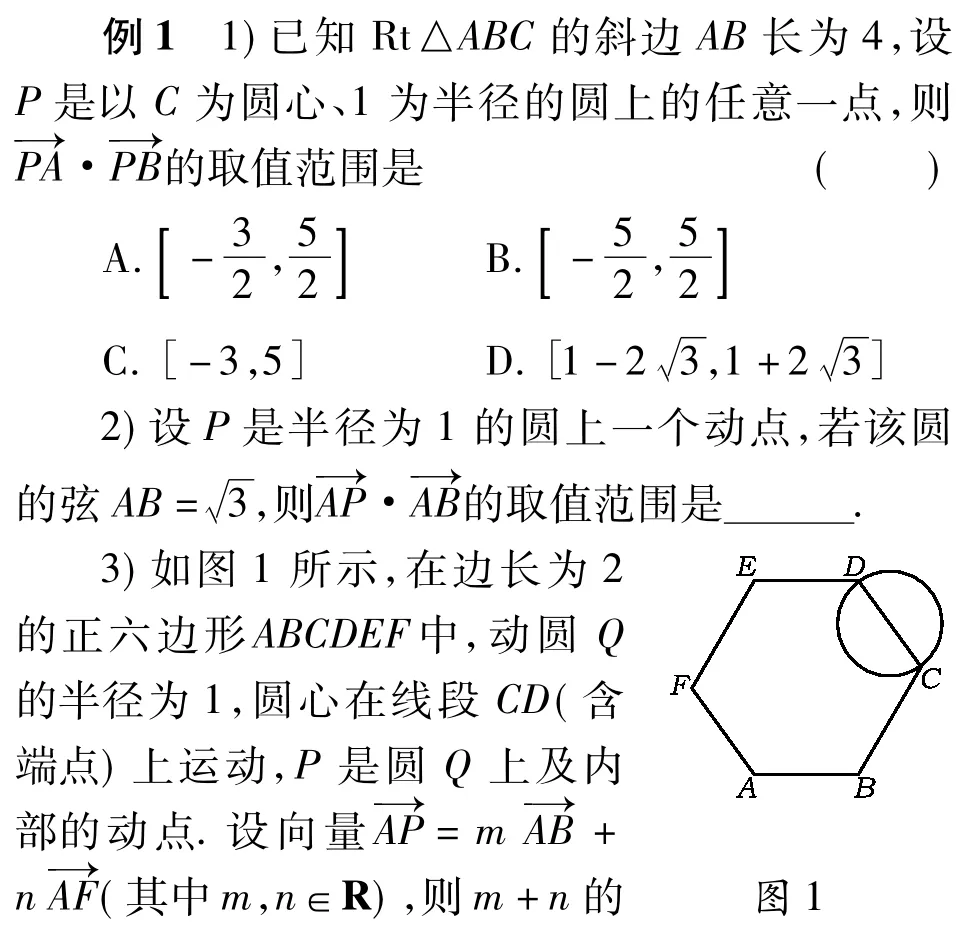
评注借助于图形或图像的直观来帮助学生理解抽象的数学概念“共线定理”，这一问题串从难度上递进，一步步深化到理解平面向量的基本定理.

2 结构思维型

任何事物都有结构，把握结构就抓住了事物本质.结构思维是根据事物的结构特征来把握事物本质的一种思考方法，数学运算中要观察数学运算式的代数结构，以便确定运算方向，简化运算过程，达到迅速、准确运算的目的.但是目前在小学、初中、高中的数学教学中，教师不够重视这一问题，学生习惯于使用计算器进行数字运算，导致运算推理繁杂.因此，设计能够反映数式运算结构的问题串或解法串，以培养中学生的运算能力是非常重要的，如指数运算中蕴含分式结构意识的问题串:

3 比较思维型

比较事物可以发现事物的差异，寻找到事物最优、最佳的状态.数学中常用比较思维来区分逻辑思维的简洁与繁杂.通常一个问题会有不同的解法，可通过比较来发现问题求解的差异并寻找最佳解题思维.在比较中判断或理解数学概念和求解方法是问题解法串的优势，同一个问题的多种解法中，有些适合剖析数学逻辑思维细节，有些适合应试环节，不同水平的学生在比较思维的问题串中至少有一种适合自己的思维.

例3已知f(x)为偶函数，当x≥0时，

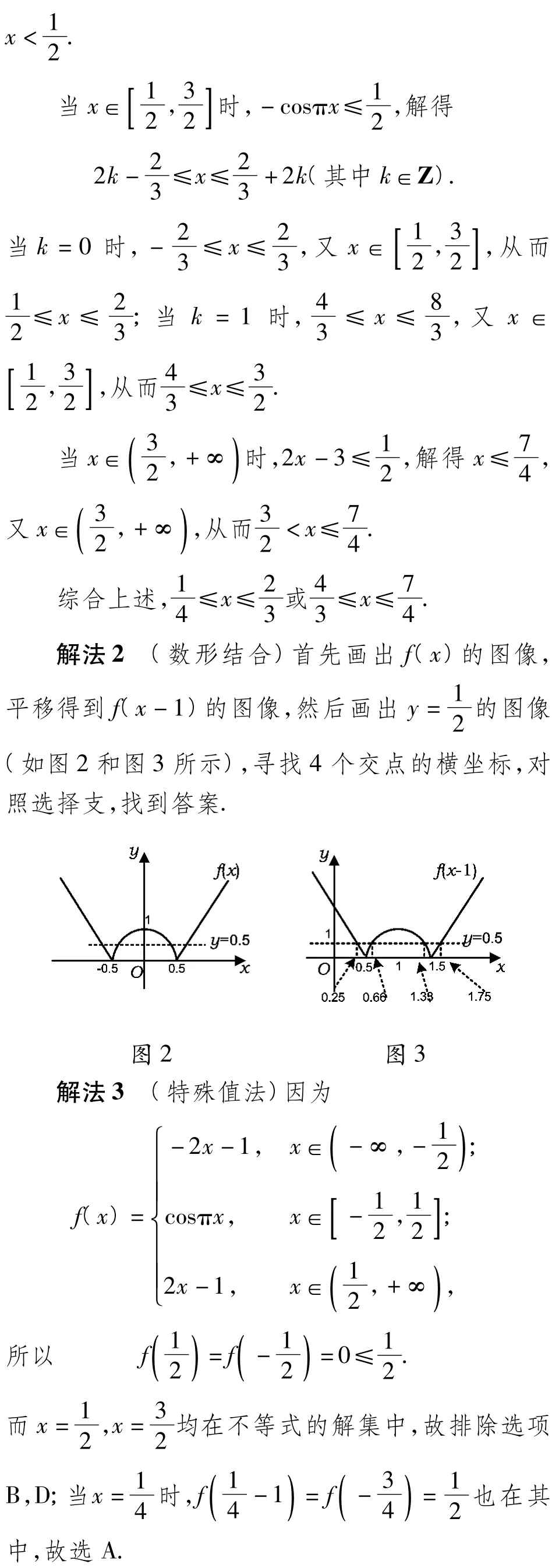
评注 解法1按照题意一步一步走下去，抓住偶函数的性质写出f(x)的表达式，借助平移变换写出f(x－1)的表达式.由于其为分段函数，因此分段求解，过程详细，思维严谨，但不宜作为应试解法.解法2首先画出f(x)的图像，平移得到f(x－1)的图像，由找到4个点的横坐标，快速寻找到问题的解.解法3寻找恰当科学的点是关键，选准进行检验，排除选项B，D;然后分析选项 A，C，在数轴上画出区间，特殊值选择有2种方案:一是选择，因其满足，故还要检验才能排除;二是选择，因其满足，故选A.

3种解法的思维训练，既有解法1的逻辑推理思维训练，明白算理，培养运算能力;又有解法2、解法3的应试训练，选择捷径，节约时间.3种解法都必须具备基本功，计算能力、分析能力、画图能力、变换能力.不同思维能力的人，在上述问题解法串设计中至少能找到一种是可接受的或有效的，使教学的有效性得以实现.

［1］ 章建跃.发挥数学的内在力量为学生谋取长期利益［J］.中国数学教育，2013(1/2):3-6.