关注过程 凸显应用——一道应用型试题的命题过程及其思考

●潘小梅 (江东区教研室 浙江宁波 315000)

关注过程 凸显应用
——一道应用型试题的命题过程及其思考

●潘小梅 (江东区教研室 浙江宁波 315000)

应用题是一类以实际问题为情境、围绕客观实际进行设问的试题.因为它不仅涉及数学知识和方法，还涉及生活、生产、社会和自然界中的问题，所以对命题者提出了较大的挑战.但由于它能全面考查学生综合运用数学知识建立有效模型解决数学问题的能力，因而成为历年中考的必考题型之一.笔者在2014年中考模拟试卷中编制了一道应用型试题，试题因其时尚的理念、新颖的形式、合理的设问备受关注.现与各位同行交流其命制过程.

1 试题展示

试题由问题、对话、解决3个部分组成，具体如下:

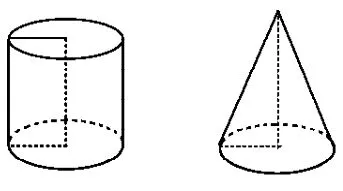
图1

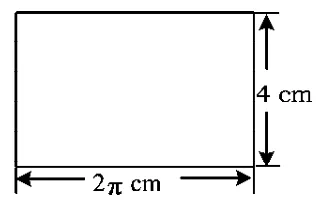
图2

例1 问题图1是底面半径都为1 cm、母线长都为2 cm的圆柱体和圆锥体模型，现要用长为2π cm、宽为4 cm的长方形彩纸(如图2所示)装饰圆柱、圆锥模型表面.已知一个圆柱和一个圆锥模型为一套，长方形彩纸共有122张，用这些纸最多能装饰多少套模型呢?

对话

师:长方形纸可以怎么裁剪呢?

生1:可按图3方式裁剪出2张长方形.

生2:可按图4方式裁剪出6个小圆.

生3:可按图5方式裁剪出1个大圆和2个小圆.

图3

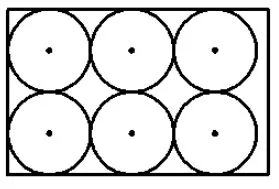
图4

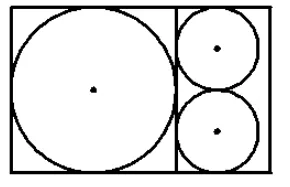
图5

师:尽管还有其他裁剪方法，但为了裁剪方便，我们仅选用这3位同学的裁剪方法.

解决

1)计算:圆柱的侧面积是______cm2，圆锥的侧面积是______cm2.

2)1张长方形彩纸剪拼后最多能装饰______个圆锥模型;5张长方形彩纸剪拼后最多能装饰______个圆柱模型.

3)求用122张彩纸最多能装饰的圆锥、圆柱模型套数.

2 解法探究

1)4π，2π.2)2，6.

3)解法1设用这些纸最多能装饰x套模型.若按图5方式裁剪，每张纸可以装饰2个圆锥模型，则装饰x套圆锥模型需要张纸;若将5张纸中的3张按图3方式裁剪、2张按图4方式裁剪可以做6个圆柱，则装饰x套圆柱模型需要张纸.根据题意得，解得，由于x是6的倍数，取x=90，装饰90套模型后剩下长方形纸片的张数为122－(45+75)=2张，2张纸不能装饰一套模型，因此最多能装饰90套模型.

解法2设用这些纸最多能装饰x套模型.因为每张纸可以装饰2个圆锥模型，所以可装饰2x个圆锥模型;又因为一个圆柱和一个圆锥配成一套，所以应装饰2x个圆柱模型.5张纸最多能装饰6个模型，平均每个模型需要张纸，因此2x个模型最少需要张纸.由于圆柱、圆锥所用的纸张数最多是122张，可以得到，解得，取x=45，此时可以装饰90套模型，剩余2张纸，而2张纸不能装饰一套模型，故最多能装饰90套模型.

3 命题过程

3.1 试题缘起

根据模拟试卷的题型分布，需要命制一道有实际背景的应用型试题，为了公平合理地评价学生的学习水平，试题力求原创或改编.联想到浙教版教材中一道“配套问题”的问题情境反复出现于教材中的“二元一次方程组”和“一元一次不等式”，笔者决定根据浙教版七年级下册课本中“二元一次方程组”的一道例题进行改编，使得试题源于课本又高于课本，既能有效地考查学生的学习情况，又能引发教师研究学生普遍感觉困难的“配套问题”的教学策略，发挥试题良好的导向作用.

该例题的内容如下:

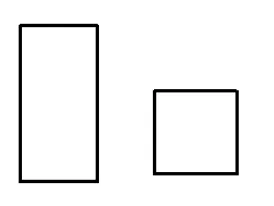
图6

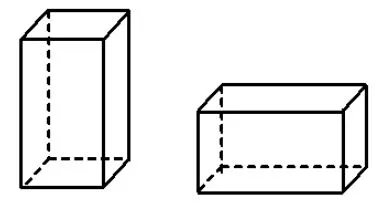
图7

例2用图6中的长方形和正方形纸板作侧面和底面，做成如图7所示的竖式和横式2种无盖纸盒.现在仓库里有1 000张正方形纸板和2 000张长方形纸板，问2种纸盒各做多少个，恰好将库存的纸板用完?

3.2 改编过程

那么，如何改编例2呢?笔者想到以下2种思路:

思路1保持例题的情境不变，改变试题考查的侧重点，比如将“方程组模型”改为“函数模型”.举例如下:

例3某工厂用如图6所示的长方形和正方形纸板做横式、竖式2种长方体形状的无盖包装纸盒(如图7所示).若有长方形纸板171张，正方形纸板82张，要做横式、竖式纸盒共50个.

1)若按纸盒的生产个数来分，有哪些生产方案?

2)已知横式纸盒的利润为每个8元，竖式纸盒的利润为每个10元，若仅从销售的利润考虑，以上哪种方案的利润最大?最大利润是多少?

此题比较容易，作为本次模拟试卷规划中的应用题不太理想.

思路2改变试题呈现形式，比如将试题中呈现的“长方体”改为其他几何体.按照这样的思路，需要找到2个有一定关联的立体图形，比如它们由相同的图形组合而成.于是想到以下2种方案:

方案1

例4如图8，将“横式无盖长方体和竖式无盖长方体”改为“正三棱柱和正三棱锥”.

图8

方案2

例5如图9，将“横式无盖长方体和竖式无盖长方体”改为“圆柱和圆锥”.

图9

显然，方案1中我们需要的是正三角形和长方形2种不同的纸片，完全可以模仿例题编制类似的试题，但是问题比较单调，是一种低水平的重复.方案2是圆柱和圆锥，圆柱的侧面展开图是长方形，圆锥的侧面展开图是扇形，这样一来，即使圆柱和圆锥的底面圆相同，也需要给出3种不同的图形，才能模仿例题来编制试题.2种图形制作立体图形的关系已经错综复杂，更不要说3种图形的组合，一时陷入窘境.仔细思考下去，这些形状的纸片从何而来?一定是用统一的纸片裁剪而来的，于是想到了利用长方形纸片来裁剪出各种需要的图形:长方形、小圆、扇形，这样圆柱、圆锥模型的个数就取决于长方形纸片的张数安排了.于是决定选用方案2继续研究.

接着开始画图思考怎样的长方形纸片可以裁剪出圆柱侧面(长方形)、圆柱底面(圆)、圆锥底面(圆)、圆锥侧面(扇形)?通过多次尝试，画出了以下4种裁剪方法(如图10所示):

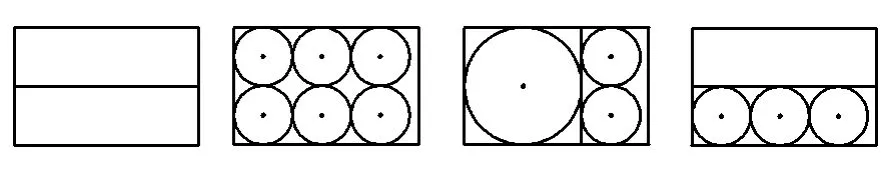
图10

接下来遇到的问题是:裁剪方法其实还远不止以上4种，不可能让学生在考试中有如此周密的思考，更何况这么多裁剪方法若都允许，则无疑会给问题的解决增添很大的难度.于是，决定舍弃第4种裁剪方法，那么怎样将其他3种裁剪方法“暗示”给学生?又怎样告知其他的裁剪方法不用考虑?一种方式就是以“云图”形式温馨提醒学生，但比较直白且至少需要2个云图，在排版上也有困难，那么何不营造“师生对话”的场景呢?让学生感受到解决试题的过程犹如平时课堂教学中师生对话的情景，并在对话的过程中进行暗示和引导.

接下来考虑试题的设问.由于解决问题中提出的“纸张分配问题”没有一定的程式，学生需要把实际问题抽象成数学问题，经过建模并综合运用数学知识解决问题，确实有一定的困难.为了合理地控制难度，笔者计划帮助学生设置台阶.学生要解决“纸张分配问题”，首先要知道如何合理安排彩纸做圆柱、圆锥模型，显然为了使做出的圆柱、圆锥模型个数最多，纸张应尽可能少浪费.那么，学生在解决该问题时应该怎样有序地进行思考呢?要弄清楚圆柱、圆锥模型所需纸怎样裁剪，这些纸怎样组合在一起比较节省.于是按从易到难、从特殊到一般的要求设计了既有关联又层层递进的3个小题:第1)小题让学生计算圆柱、圆锥的侧面积，入口低，让所有学生都有信心参与本题的解决.第2)小题的主要目的是帮助学生理清“圆柱、圆锥的裁剪方法”，提出“一张长方形彩纸剪拼后最多能装饰几个圆锥模型”，必然使得学生思考发现用图10所示的第3种裁剪方法能做成2个圆锥模型，也使得学生通过这个小题联想到第1和第2种裁剪方法也可以做圆柱模型.紧接着设问“5张长方形彩纸剪拼后最多能做几个圆柱模型”，使得学生思考“怎样合理组合可以使得做成的圆柱模型最多”.在这里，由于5张纸数量少，学生通过充分地思考后能够认识到3张裁剪为长方形、2张裁剪为小圆组合最多有6个圆柱模型，同时也为第3)小题作较好地铺垫.第3)小题要求学生解决最初提出的问题“用122张纸最多能装饰多少个圆柱和圆锥模型”，达到了对学生思维深度的充分考查，较好地考查了学生综合运用知识解决问题的能力.

4 命题说明

4.1 发挥试题的评价导向功能

本道应用型试题(例1)让人耳目一新，它的情境取材于课本中的一道例题(例2)，背景公平，通过从易到难的3个小问题，不仅考查了圆柱和圆锥侧面展开图的形状及其计算，还考查了学生综合运用图形组合、不等式模型解决实际问题的能力以及化归、数形结合等思想方法，较好地考查了知识技能、数学思考、问题解决，发挥了试题良好的评价导向功能.

4.2 关注学生学习过程的考查

本题先提出需要解决的问题，让学生通过阅读“师生对话”帮助学生思考，通过理解、分析、计算逐步寻求解决问题的策略，经历“问题提出→问题思考→问题解决”的过程，关注了过程与方法、数学思考、创新思维、学习能力的考查，倡导了学生自主思考的新课程理念，将考试评价的过程变成一种指导学生自主思考解决问题的过程.

4.3 体现应用型试题的命题特点

由于应用型试题往往具有一定的实际背景，又要蕴含丰富的数学知识，因此命制应用题时需要在试题的表述上下大功夫，努力减少文字量，使语义简洁通俗、形式活泼.本题以“师生对话”的形式真实再现了课堂中教师引导学生思考的情景，又把“裁剪方法”暗示其中，使得试题贴近学生，呈现形式新颖，表述简洁，降低了考试本身带给学生的心理压力.

潘小梅，女，浙江省宁波市江东区初中数学教研员，曾获浙江省优秀教研员、宁波市名师、宁波市优秀教师、宁波市骨干教师、中国数学奥林匹克教练员、全国初中数学竞赛优秀辅导教师等荣誉称号，多次参与浙江省宁波市中考、数学竞赛的命题工作，广受好评.在《中学数学教学参考》、《数学教学》、《中国数学教育》、《中学教研(数学)》等各类数学期刊发表文章50余篇，其中5篇被中国人民大学报刊复印资料中心全文转载.多年来，主持省、市多项重点规划课题，多次荣获省、市级基础教育教研课题一、二等奖，近5年应邀各地讲学、上课100多次，学术成果在全国各地有较大影响力.