GPS快速定位中相位模糊度动态解算的一种正则化方法

段 荣，赵修斌，庞春雷，李 媛，伍劭实

（1. 空军工程大学 信息与导航学院，西安710077；2. 94153部队，陕西 咸阳 712200）

GPS快速定位中相位模糊度动态解算的一种正则化方法

段 荣1，赵修斌1，庞春雷1，李 媛2，伍劭实1

（1. 空军工程大学 信息与导航学院，西安710077；2. 94153部队，陕西 咸阳 712200）

针对GPS快速定位中少数历元组成的法方程存在严重病态性的问题，研究了GPS单频整周模糊度快速解算的新方法：即首先采用改进 SVD分解获得系数矩阵的精确奇异值，避免了较小奇异值抖动的影响；然后基于改进SVD分解结合法矩阵病态性特点，设计了一种改进Tikhonov正则化方法，合理构造了正则化矩阵，有效抑制法矩阵的病态性。算例表明：与LS估计-LAMBDA方法和Tikhonov正则化-LAMBDA方法相比，新方法能够有效降低法矩阵的条件数约3个数量级，仅解算4个历元数据，浮点解偏离真值的方差从41.89减小到1.04，可以快速获得准确、稳定的模糊度浮点解。模糊度固定性能结果进一步表明，新方法显著地提高模糊度搜索效率和成功率，解算成功率提高100%。

改进Tikhonov正则化；整周模糊度；病态性；SVD分解；成功率

利用GPS载波相位作为观测值进行高精度的快速定位，如飞机精密进近着陆/着舰、编队飞行、航天器交会对接等，其关键是快速可靠地固定整周模糊度[1]。整周模糊度的快速准确解算主要体现在两个方面，一是准确浮点解的快速求解，二是固定解的快速搜索。近年来，国内外众多学者都在致力于研究整周模糊度的快速解算，成果如[2-5]：双频P码伪距法、最小二乘搜索法（LS）、模糊度函数法、快速模糊度确定法（FARA）、Cholesky分解法、ARCE算法和LAMBDA算法等。其中，Teunissen教授提出的LAMBDA算法是国际公认的理论上最为严密、解算最为有效的方法。上述大多算法是基于双频观测值提出的，而且主要侧重于搜索环节的优化改进。事实上，在观测历元较少的情况下，由于观测信息不足或者卫星几何图形变化较小将导致法矩阵的严重病态，采用传统最小二乘估计方法，或无法解算或解算结果与真实值偏差较大，不能满足动态定位的实时性需求。为此，相关学者针对病态问题开展了浮点解快速解算方面的研究，相应方法有岭估计法、TSVD法、欧吉坤团队提出的修正Tikhonov正则化法及基于改进型UDVT分解的正则化方法等[6-8]。但际应用表明，岭估计存在岭参数确定困难问题；TSVD法直接将小的奇异值删除将损害解估计的分辨率[7]；修正的Tikhonov正则化方法采用奇异值分解构造新的正则化矩阵，仅用5个历元的观测数据准确固定了整周模糊度，但其没有考虑病态矩阵在奇异值分解过程中小奇异值扰动的影响[8][9]。

本文在前期的研究基础上，首先对双差方程病态性进行了分析，采用改进SVD分解获得系数矩阵的精确奇异值，避免了较小奇异值抖动的影响，然后依据法矩阵病态结构特性，设计了一种改进Tikhonov正则化新方法，并充分结合GPS快速定位中（观测历元数较少）法矩阵总存在三个数值接近于0的奇异值的共同特点，合理构造了正则化矩阵，有效抑制法矩阵的病态性，获得了更高精度且稳定的模糊度浮点解及相应的均方误差阵，以均方误差阵代替协方差阵并运用LAMBDA算法，可快速准确地固定模糊度。

1 常规方法及解算

1.1 双差方程病态性分析

1.2 病态方程解算

若一个问题的解存在、惟一且稳定，则称该问题是适定的，否则，即不满足其中的任何一个就称为不适定（ill-posed）[9]。不满足解稳定的条件，则称问题是病态的。GPS快速定位是一个典型的不适定问题。正则化方法是求解上述不适定问题的有效方法，基本思想是对不适定方程加上某种正则条件，转化为适定方程，从而获得准确稳定的解。常用的正则化方法有岭估计法、截断奇异值分解法(TSVD)、Tikhonov正则化法等。基于SVD分解的TSVD方法和Tikhonov正则化方法中，较大的奇异值及其对应的奇异值向量表示模型参数中较为确定和可靠的部分，而较小的奇异值及其对应的奇异值向量则表示不可靠的部分。TSVD法解决不适定问题的方法是直接截掉较小的奇异值及其对应的奇异值向量，从本质上删除了模型中不可靠的部分，但此方法可能有损解估计的分辨率。

病态方程求解，最著名且比较有效的解法是Tikhonov正则化方法[9-10]，根据Tikhonov正则化原理，求解观测方程(3)即是寻求满足如下估计准则的解：

2 新算法

GPS快速定位中法方程系数矩阵具有共同特点，即明显存在3个数值很小（接近于0)的奇异值，正是由于小奇异值对基线对应分量约束不够导致无法得到准确的浮点解[8,10-11]。针对N0总存在跳跃较大的小奇异值的情况，由矩阵扰动理论结合Bauer-Fike定理[12]，在矩阵病态时进行奇异值分解，若较小的奇异值发生抖动（如10-8大小），将引起约束条件恶化导致参数向量解精度的大大降低。因此，需要通过构造新的矩阵分解，以期获得更加精确的奇异值。本节首先采用了改进SVD分解方法，然后基于法矩阵特点给出了一种正则化矩阵的构造新方法。

2.1 改进SVD分解方法

2.2 正则化矩阵构造新方法

针对法矩阵的结构特性，本文设计了一种新的构造正则化矩阵的方法。采用2.1节改进的SVD分解方法对作奇异值分解，则有：

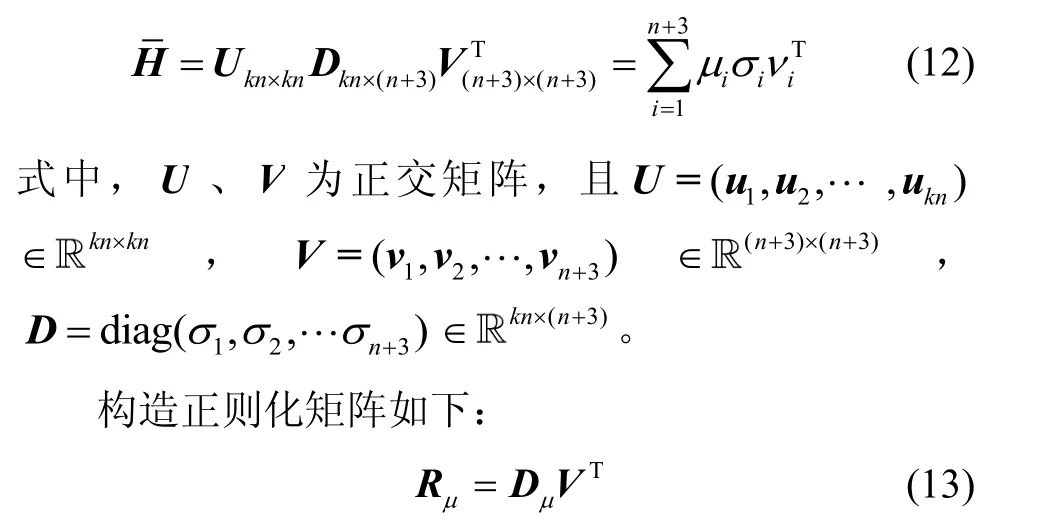
式中，

下面从正则化滤子函数的角度考虑本文改进Tikhonov正则化法的合理性和正确性。引入正则化滤子函数后近似正则解为：

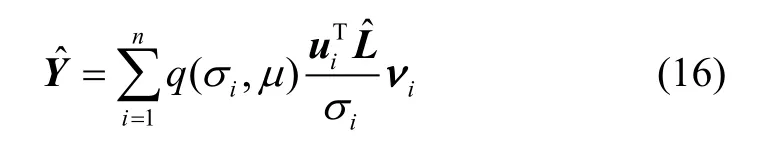
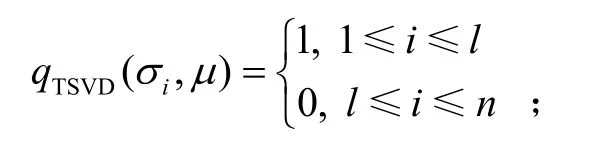
标准Tikhonov正则化滤子函数为

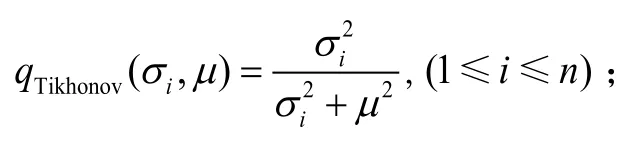
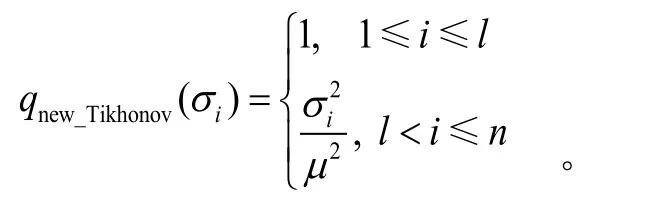
由以上滤子函数比较容易得出，改进Tikhonov正则化法在段与TSVD法相同，在区间内与标准 Tikhonov正则化形式一致。因此，结合1.2节的分析可知，改进Tikhonov正则化法兼具TSVD法和Tikhonov正则化法的优点，去伪存真，既修正了较小的奇异值，不损害解估计的分辨率，又抑制了对较大奇异值修正的影响，避免了模型中可靠部分发生畸变从而增大误差，可以获得更为精确的正则化解。

结合GPS快速定位中（观测历元数较少）法矩阵总存在三个数值接近于0的奇异值的共同特点，在利用式(13)构造正则化矩阵选择其分块形式

式中，正则化参数可以应用L-曲线法[13]来选取，本文选取正则化参数102。

与式(4)相比，法矩阵中增加了R μ=-项。正是由于有

即得到最优的整数解估计值。

3 算例分析

为进一步验证算法，2014年12月19日下午19时，在空军工程大学桃园校区实验楼楼顶利用 2个NovAtel接收机板卡进行实验观测，两天线分别固定在已知基线长度为2.613 m的基线板两端，基线仰角和方位角分别为-36.41°、102.96°。数据采集时间为 5 min，采样率为1 s，截止高度角设为10°。整个观测实验中两测站共视卫星为 PRN29、PRN3、PRN14、PRN16、PRN20、PRN25、PRN31、PRN32，选取仰角最大的PRN29号星作为基准星，可以组成7个卫星对：(29 -3)、(29 -14)、(29 -16)、(29 -20)、(29 -25)、(29 -31)、(29 -32)，通过全部数据解算得到的模糊度解为[14 -1 761 982 16 6 626 631 -1761 977 -1 761 978 -4]，以此作为整周模糊度的真实值。

为体现动态精密测量用户对定位需求的快速性，本文选取前4个历元的观测数据，用以下3种方法进行模糊度解算：

方法1：本文新方法；

方法2：LS估计-LAMBDA方法；

方法3：Tikhonov正则化-LAMBDA方法。

这3种方案求解模糊度方法的结果比较如表1所示。

由表1可知，标准Tikhonov正则化法解算的模糊度浮点解比LS方法逼近真实值，LS方法由于观测历元数较少，法方程严重病态，最终无法正确固定整周模糊度。应用本文方法能够有效降低法矩阵的条件数，改善法方程的病态性，仅解算四个历元数据，本文改进 Tikhonov正则化方法可以得到与模糊度真实值更为接近的浮点解，继而结合LAMBDA搜索得到了准确的整周模糊度值，具有更高的精度和可靠性。

为了更好地验证本文算法的可靠性及准确性，本文研究了在观测矩阵添加扰动前后本文算法与文献[6]所提方法的解算性能比较。观测矩阵中包含扰动相当于人为地给观测矩阵添加一个同维数的较小的扰动矩阵，本文取法为，除第2行第2列元素，即取值0.0007外，其余元素均为零。结果比较如表2所示。

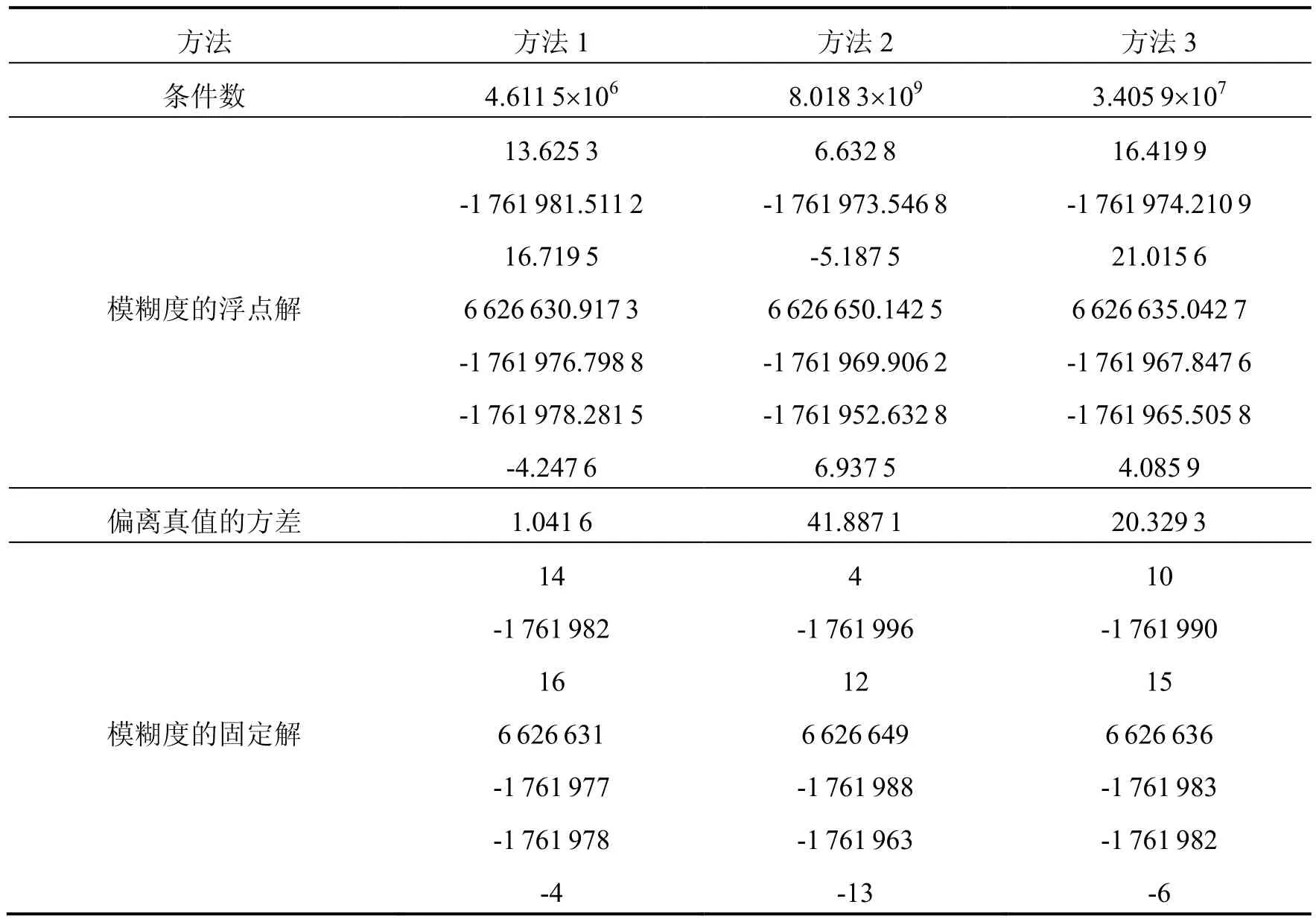
表1 三种方法解算结果的比较Tab.1 Comparison on the calculation results of the three methods

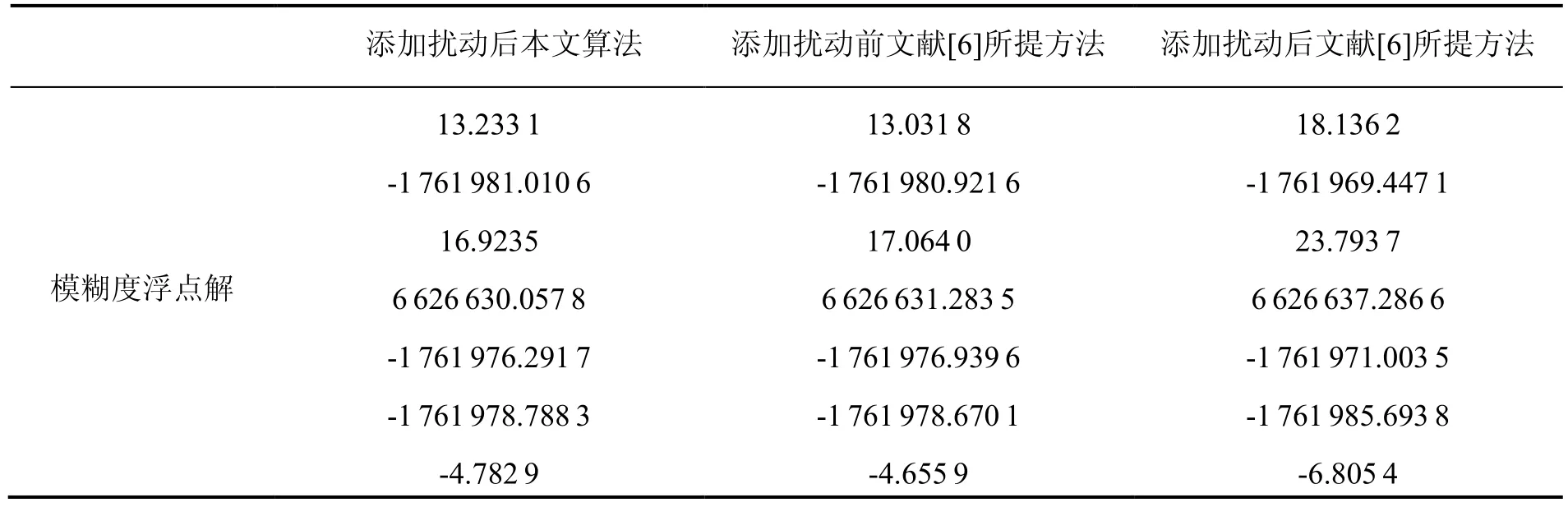
表2 观测矩阵中添加扰动情况下的结果比较Tab.2 Comparison on the calculation results when observation matrix contains disturbance

由表2可知，在病态的观测矩阵添加扰动后，从解算的模糊度浮点解来看，文献[6]所提方法在添加扰动前后表现比较敏感，而本文方法在添加扰动前后模糊度浮点解变化较小，具有较好的稳定性。这是因为本文方法采用改进的 SVD分解方法获得了较为精确的奇异值，避免了小奇异值发生抖动造成正则化矩阵不稳定，最终引起浮点解精度的损耗，说明本文算法具有较好的稳定性。

图1 新方法解算的基线长度及其误差Fig.1 Length of baseline and its error using new method

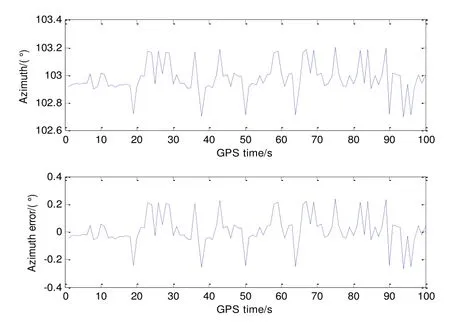
图3 新方法解算的基线方位角及其误差Fig.3 Azimuth of baseline and its error using new method

用方法1解得的模糊度固定解反代式(1)求解基线向量及基线俯仰角、方位角并与准确值进行比较得到其误差，分别如图1、图2和图3所示。

由图1、图2和图3可以看出，利用本文算法解算的基线长度误差在1 cm范围内，俯仰角与方位角误差也在0.4°范围内，满足精度要求，说明新算法具有一定的准确性。

为了进一步验证本文改进方法在改善模糊度固定成功率方面的性能，随机选取采集数据中连续168个历元的观测数据，从1～4历元为一组，2～5历元为下一组，可得到165组数据，分别采用方法1和方法2进行解算比较。法矩阵条件数对比图如图4所示。由图4可知：通过改进算法，正则化使法矩阵条件数减小约103量级，病态性程度得到有效改善。

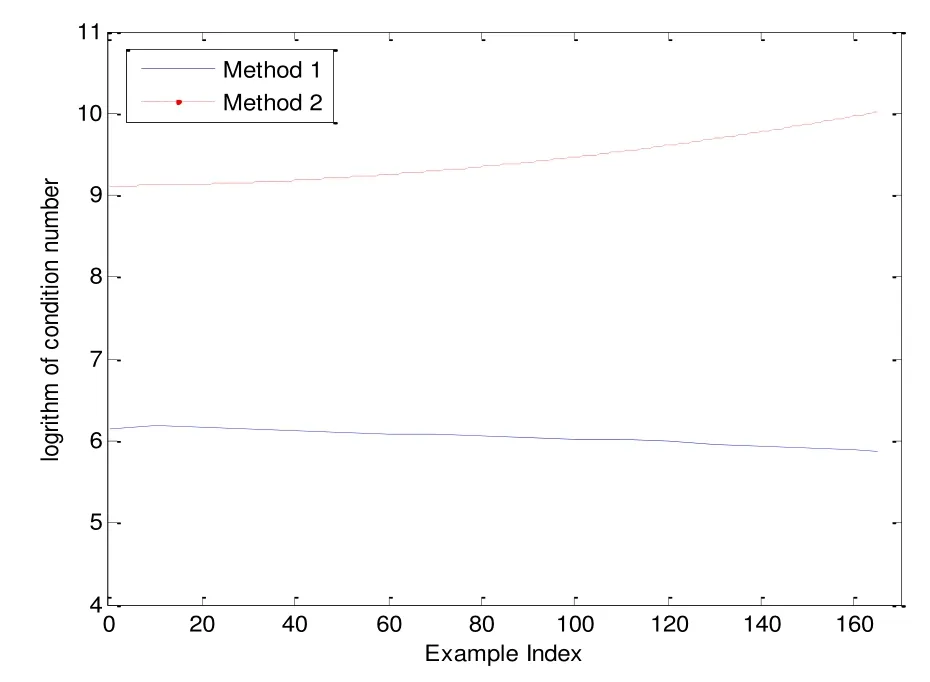
图4 法矩阵条件数对比图Fig.4 Comparison on condition numbers of norm matrix

选取模糊度精度因子（ADOP，ambiguity dilution of precision）和模糊度解算成功率作为评估整周模糊度固定性能的指标参数，ADOP 是Teunissen教授提出的用于衡量模糊度解算精度的重要指标[16]，其精度直接影响搜索空间和候选解个数，并且通过ADOP可以直接计算模糊度固定的成功率上限。ADOP计算公式为

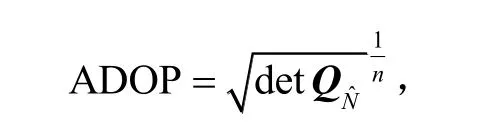
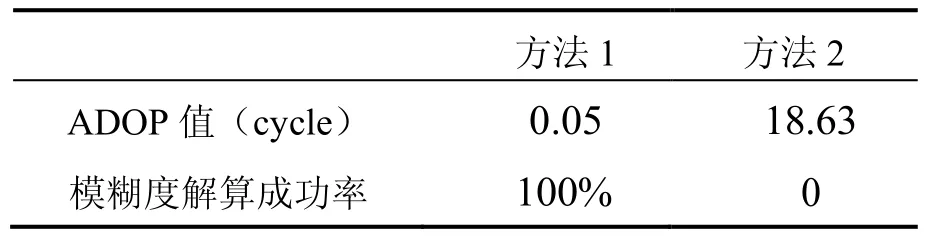
表3 模糊度解算性能的对比Tab.3 Comparison on AR performances

模糊度解算性能对比结果如表3所示。与方法2相比，本文算法利用均方误差阵代替协方差阵进行LAMBDA搜索，缩小了模糊度搜索范围，在4个历元内，ADOP值较小，表明精度较高，有效减小了模糊度搜索空间和候选值组数，提高了模糊度搜索效率。与方法2不能准确固定相比，方法1的165组数据解算都能得到比较接近的浮点解，并实现正确固定，成功概率由0增加到100%，说明本文算法能够显著提高模糊度解算成功率。

4 结 论

本文以模糊度解算的浮点解快速求解环节作为切入点，针对GPS高精度快速定位应用中少数历元组成的法方程存在严重病态性的问题，提出了一种GPS单频整周模糊度快速解算的方法。通过对实测数据的算例分析，得到如下结论：

① 利用改进Tikhonov正则化法，兼具TSVD法和Tikhonov正则化法的优点，去伪存真，既修正了较小的奇异值，不损害解估计的分辨率，又抑制了对较大奇异值修正的影响，避免了模型中可靠部分发生畸变从而增大误差，通过合理构造了正则化矩阵，有效改善了法矩阵的病态性，获得了更高精度且稳定的模糊度浮点解。

② 采用改进SVD分解获得系数矩阵的精确奇异值，避免了较小奇异值抖动的影响，增强了算法的抗扰动能力。

③ 算法仅利用 4个观测历元数据即实现了模糊度浮点解的快速解算与固定，且显著提高模糊度解算的效率和固定成功率。

本文算法在观测4个历元时即可快速可靠的固定模糊度及定位定姿，因此为单频接收机在高精度快速相对定位，如精密进近着陆/着舰、编队飞行、航天器交会对接等领域的广泛应用，提供了新的研究思路。

（References）：

[1] Li Bao, Cao Ke-jin, Xu Jiang-ning, et al. Application of carrier phase differential relative navigation for shipboard landing of aircraft[C]//China Satellite Navigation Conference (CSNC) 2013 Preceedings. Springer Berlin Heidelberg, 2013: 189-196.

[2] Xu Pei-liang. Parallel Cholesky-based reduction for the weighted integer least squares problem[J]. Journal of Geodesy, 2012, 86(1): 35-52.

[3] Teunissen P J G. Integer least-squares theory for the GNSS compass[J]. Journal of Geodesy, Springer, 2010, 84: 433- 447.

[4] Li Bo-feng, Verhagen S, Teunissen P J G. GNSS integer ambiguity estimation and evaluation: LAMBDA and Ps-LAMBDA[C]//China Satellite Navigation Conference (CSNC) 2013 Preceedings. Wuhan, China, 2013: 291-301.

[5] Liu Hai-ying, Chen Zhi-ming, Ye Wei-song, et al. GNSS carrier phase ambiguity resolution based on integrity restriction in ambiguity domain[J]. Advances in Space Research, 2014, 53: 1207-1218.

[6] 欧吉坤, 王振杰. 单频 GPS快速定位中模糊度解算的一种新方法[J]. 科学通报.2003, 12, 48(24): 2572-2575. Ou Ji-kun, Wang Zhen-jie. A new method of ambiguity resolution in single frequency GPS quickly positioning[J]. Chinese Science Bulletin, 2003, 48(24): 2572-2575.

[7] 吴太旗, 邓凯亮, 黄谟涛, 等. 一种改进的不适定问题奇异值分解法[J]. 武汉大学学报·信息科学版, 2011, 36(8): 900-904. Wu Tai-qi, Deng Kai-liang, Huang Mo-tao, et al. An improved singular values decomposition method for ill-posed problem[J]. Geomatics and Information Science of Wuhan University, 2011, 36(8): 900-904.

[8] 庞春雷, 赵修斌, 卢艳娥, 等. 基于改进型UDVT分解的单频整周模糊度快速解算[J]. 航空学报, 2012, 33(1): 102-109. Pang Chun-lei, Zhao Xiu-bin, Lu Yan-e, et al. Algorithm of rapid integer ambiguity resolution for single frequency GPS receivers based on improved UDVT decomposition [J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(1): 102-109.

[9] Li B, Shen Y, Feng Y. Fast GNSS ambiguity resolution as an ill-posed problem[J]. Journal of Geodesy, 2010, 84 (11): 683-698.

[10] 李豹, 许江宁, 曹可劲, 等. 改进 LAMBDA算法实现单频GPS整周模糊度快速解算[J]. 中国惯性技术学报. 2013, 21(3): 365-368. Li Bao, Xu Jiang-ning, Cao Ke-jin, et al. Fast resolution of single frequency GPS integer ambiguity realized by improved LAMBDA algorithm[J]. Journal of Chinese Inertial Technology, 2013, 21(3): 365-368.

[11] 柯福阳, 王庆, 潘树国. 网络 RTK参考站间模糊度动态解算中病态方程的一种解算算法[J]. 中国惯性技术学报, 2008, 16(6): 676-681. Ke Fu-yang, Wang Qing, Pan Shu-guo. A method of ill-posed equation resolution for ambiguity resolution on-the-fly in network RTK reference station[J]. Journal of Chinese Inertial Technology, 2008, 16(6): 676-681.

[12] Yang X, Zhu J J, Xu Jiang-ning. Singular perturbation margin assessment of linear time-invariant systems via the Bauer-Fike theorems[C]//2012 IEEE 51st Annual Conference on Decision and Control. 2012: 6521-6528.

[13] Nagy A M. On the numerical solutions of ill-posed problems[M]. LAP LAMBERT Academic Publishing, 2013.

[14] Teunissen P J G. The least-squares ambiguity decorrelation adjustment: a method for fast GPS integer ambiguity estimation[J]. Journal of geodesy, 1995, 70: 65-82.

[15] Verhagen S, Teunissen P J G. The ratio test for future GNSS ambiguity resolution[J]. GPS Solutions, 2013, 17 (4): 535-548.

[16] Monico J F G, Rofatto V F, Mendonca M A M D. Introduction and application of the GNSS ambiguity dilution of precision-ADOP[J]. Boletim De Ciencias Geodesicas, 2014, 20(2): 279-299.

Regularization approach for dynamic resolution of phase integer ambiguity in GPS rapid positioning

DUAN Rong1, ZHAO Xiu-bin1, PANG Chun-lei1, LI Yuan2, WU Shao-shi1
(1. Information and Navigation College, Air Force Engineering University, Xi’an 710077, China; 2. Unit 94153 of PLA, Xianyang 712200, China)

In view of the ill-condition of normal matrix which is formed by few epoch observations in GPS rapid positioning, a new ambiguity resolution method was proposed, in which the modified singular value decomposition (SVD) is designed to acquire the accurate singular values of coefficient matrix, which avoids the influence of small singular value disturbance. Then an improved Tikhonov regularization method is proposed, and a regularizer matrix is constructed based on the characteristics of ill-condition matrix and modified SVD. Experimental example shows that, compared with least squares estimation and Tikhonov regularization combining with LAMBDA algorithm, the improved method has reduced the condition number of normal matrix by about 3 orders of magnitude, and has reduced the variance of float ambiguity deviated from true value to 1.04 from the original 41.89. As a result, a more accurate and stable float solution can be quickly obtained only by the L1-frequency data of four epochs, while the success rate is improved to 100%.

improved Tikhonov regularization; integer ambiguity; ill-condition; singular value decomposition; success rate

V557

：A

2015-06-12；

：2015-09-20

国家自然科学基金项目（61273049）；陕西省自然科学基金项目（2014JM8309）

段荣（1986—），男，博士研究生，从事卫星导航高精度定位研究。E-mail：duanrong0919@163.com

联 系 人：赵修斌（1965—），男，教授，博士生导师。E-mail：zhaoxiubin926@163.com

1005-6734(2015)05-0624-07

10.13695/j.cnki.12-1222/o3.2015.05.012