柴油机双层隔振非线性系统主动隔振研究

肖 斌，高 超，张艾萍，刘志刚

(1.东北电力大学 能源与动力工程学院，吉林 132012;2.哈尔滨工程大学 动力与能源工程学院，哈尔滨 150001)

近些年，振动主动控制在理论、技术和方法上均得到长足发展，已在航空航天、船舶、车辆工程等领域得到广泛应用［1］，并在动力装置［2］、设备和结构［3］等减振降噪方面发挥愈来愈重要的作用。在振动主动控制中，因耦合作用被加强、打破小振动状况［4］或因选用非线性吸振器、隔振器等［3，5］而引入系统非线性，抑或因加入主动执行结构而不可避免地带来误差通道非线性［4，6］，使得系统在振动传递、响应环节均具有非线性。系统非线性，会掩盖系统线性环节结构动力特征，终将影响动力系统的建模、振动分析、控制策略设计的合理和有效性，甚至淹没振动主动控制效果。

在振动主动控制试验室研究中，采用船用柴油机作为初级振源、液压伺服系统作为主动控制作动器，构建柴油机双层隔振系统［1，7－8］;其对象系统研究，历经集中质量的两自由度模型、两质量12自由度模型［9］以及多体耦合的刚体模型、柔体模型［10］等振动系统模型分析;其振动主动控制策略研究，在模拟台架上包括自适应 MLMS 算法［8］、自适应 x－RLMS 算法［1，8］、自适应陷波算法等多种前馈控制算法和人工智能控制策略［1，7］，而试验台架上包括自适应梳状滤波算法、多误差 LMS 算法［1，8］和人工神经网络［7］等。柴油机双层隔振系统振动主动控制，在理论上已取得阶段性成果，并在试验研究中也获得较好隔振效果［11］。

然而，柴油机双层隔振系统误差通道存在严重的非线性［1］，极大地限制主动控制效果。考虑系统非线性特征，利用神经网络模型［12］、非线性控制模型［13－14］等建立非线性系统预测模型，或者利用例如Hammerstein 模型、Wiener模型、Hammerstein－Wiener模型、Wiener－Hammerstein 模型等模块化结构模型［15－17］进行非线性系统辨识，基于非线性系统模型分析设计主动控制策略。目前针对柴油机双层隔振非线性系统，基于Volterra模型进行非线性系统解耦［18］、分析非线性系统特征［19］并设计非线性系统线性化策略［4，20］通过数值仿真、试验研究进行了柴油机双层隔振系统主动隔振研究。

本文针对柴油机双层隔振系统，考虑误差通道非线性，预补偿模型参考自适应逆控制(Model Reference Adaptive Inverse Control with Pre－Compensator，PCMARIC)［20］进行误差通道非线性系统线性化，继而集成自适应陷波算法，建立自适应复合控制策略;并利用模态试验数据，基于Hammerstein型非线性系统解耦及基频广义频响函数性质，建立线性化参考模型和误差通道相频曲线模型，分析柴油双层隔振非线性系统主动隔振试验效果，发展自适应复合控制策略;并为解决振动主动控制中引入系统非线性问题，从而实现其有效振动主动控制提供一种探索。

1 柴油机双层隔振非线性系统

柴油机隔振双层隔振系统，由于隔振系统存在耦合非线性振动，加之作动器为液压伺服系统，如图1所示，导致振动主动控制误差通道存在严重的纯输入型非线性［4，20］，构成 Hammerstein 型非线性系统。

2 Hammerstein型非线性系统解耦

2.1 非线性系统解耦

考虑柴油机隔振系统主动控制误差通道为纯输入型非线性系统，其系统模型描述基于Hammerstein模型

由多项式微分方程给出，即［14］

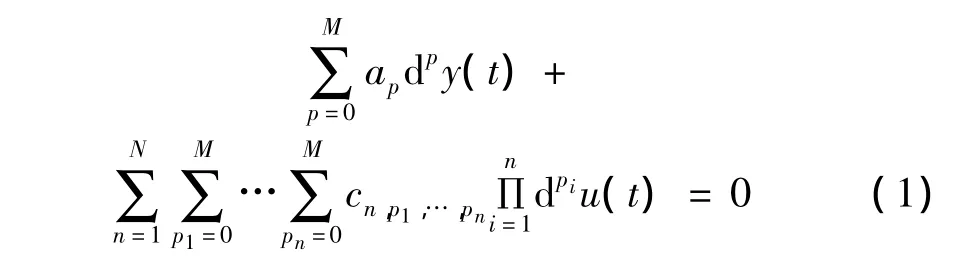
式中:t为时间，dp为p阶微分算子，ap为p阶输出系数，cn，p1，…，pn为系统非线性输入系数。

假设受到包含多个离散线谱源激励，即

其中:αki、ωki(ωk1＜ … ＜ ωkm)和 φki分别为第ki个谱线的幅值、圆频率和相角。则基于Volterra级数N阶截断模型，给出系统(1)响应为［14，18］

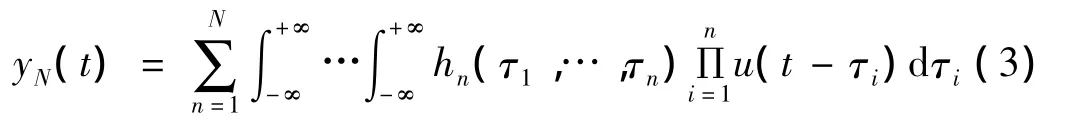
式中:yN(·)为N阶截断输出，hn(·)为n阶广义脉冲响应函数，其n维Fourier变换Hn(·)称为n阶广义频响函数(the Generalized Frequency Response Functions，GFRFs)。

在式(3)中，对激励项使用Euler公式和二项式定理可得［18］

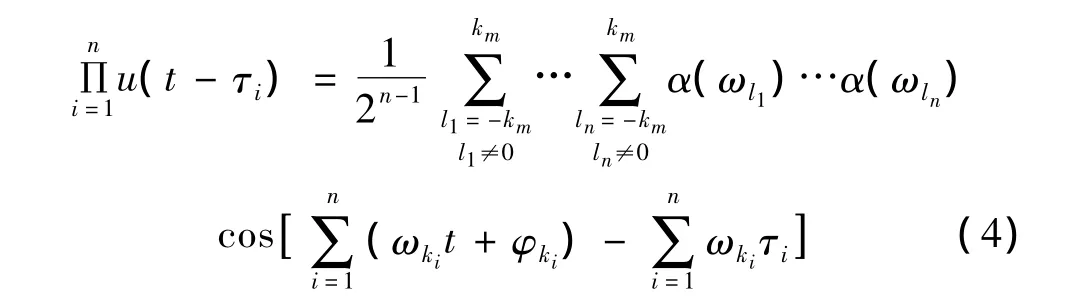
若式(2)为单频激励，ωln∈{ωk，k= ±1}，对其进行Fourier变换得到激励频谱

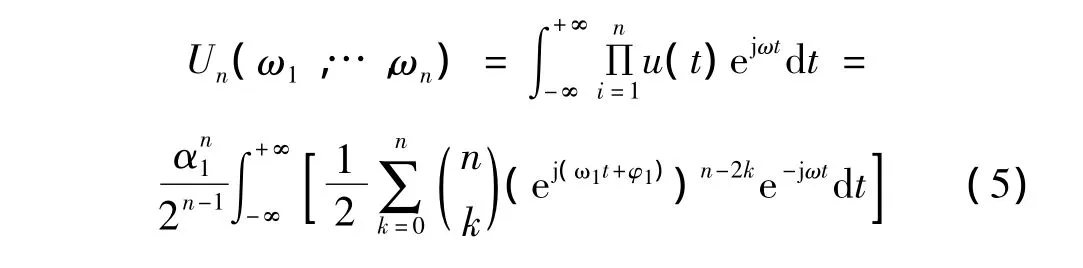
此时，系统(2)的第n阶频响输出为

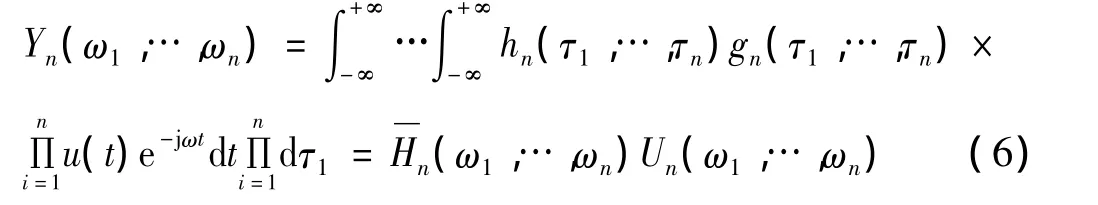
在式(5)和(6)中，激励、响应谱为“同构”函数，引入gn(τ1，…，τn)构造“同构”广义频响函数，进而对式(3)在频域进行解耦［18］，即

其中:

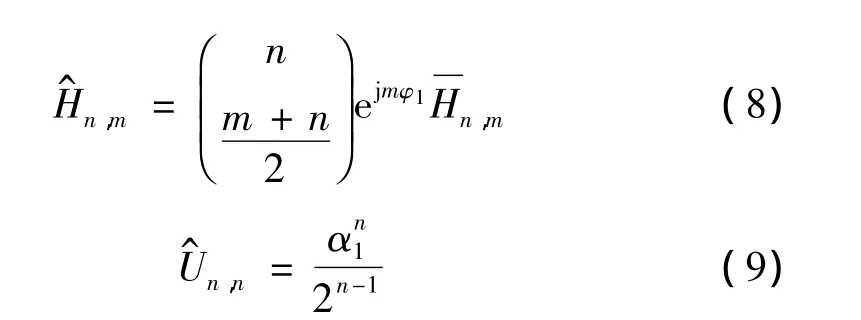
2.2 基频广义频响函数

在式(6)中，考虑广义频响函数为“同构”函数，即［18］

根据式(10)，单频ω={ω1=，…，ωn}激励时，系统在激励频率上振动响应将受到高阶次广义频响函数作用，亦即对于k=2，3，…，将对基频响应存在作用的n(=2k－1)阶广义频响函数定义为n阶基频谐振广义频响函数，即［19］

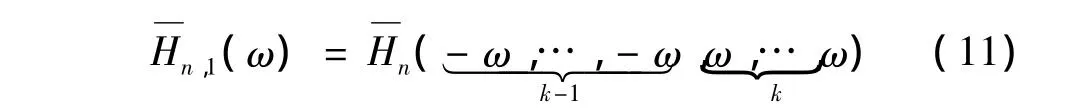
于是，结合式(7)和(11)，在单频激励下，非线性系统Hammerstein模型基频频域响应

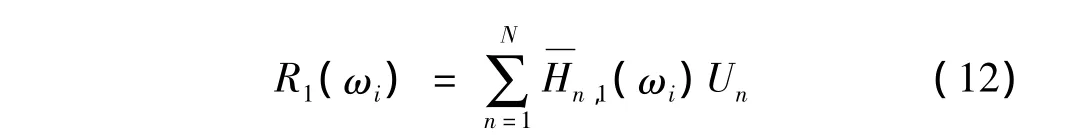
式中

另外，若忽略系统存在的非线性，根据式(12)则有

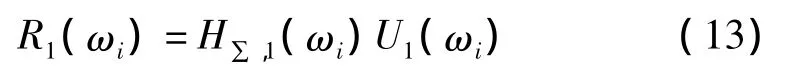
其中:U1(·)为基频输入的 Fourier变换，H∑，1为忽略系统非线性直接估计的频响函数。

因而，针对柴油机双层隔振非线性系统，结合式(7)和(11)～(13)，并基于曲线拟合技术［19］对系统误差通道频响函数进行频域估计，识别其结构动力特征，为系统主动隔振研究提供基础。

3 自适应复合控制策略

3.1 算法实现

针对柴油机双层隔振非线性系统，在误差通道非线性系统线性化的基础上，进一步集成自适应陷波算法，形成自适应复合控制策略，如图2所示。

在图2右侧红色线框中，为PCMRAIC非线性系统线性化算法［4，20］，其中包含频域预补偿器 Cp和自适应离散域补偿器CA。

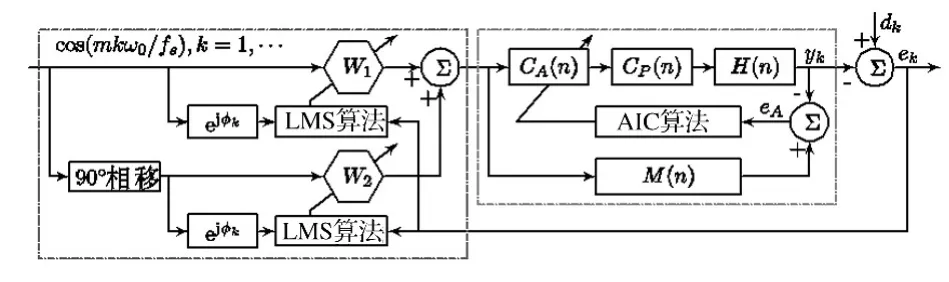
图2 自适应复合控制策略框图Fig.2 Block diagram of the adaptive hybrid control strategy

根据非线性系统多项式格式，给出系统(1)前n阶 GFRFs［14］

其中:

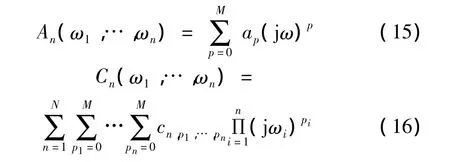
采用广义频响函数截断近似，若非线性系统(1)的GFRFs为 H={Hn(ω1，…，ωn)}、频域预补偿器 Cp的GFRFs为 G={Gn(ω1，…，ωn)}以及补偿后系统的GFRFs为 P={Pn(ω1，…，ωn)}，根据 P=G·H，且Hn(ω1，…，ωn)=0，可得预补偿器模型［14］

在式(17)给出频域预补偿器Cp的GFRFs基础上，进一步采用MRAIC控制对系统p进行离散域补偿。

对于输入U、参考模型M，假设CA得到理想的离散补偿器，有

实际与理想的离散补偿器之间的误差为

而利用自适应算法，在模型正、逆辨识过程收敛时，定义离散补偿器自适应误差［20］

根据式(18)～(20)，采用自适应算法，在模型正、逆辨识过程收敛时，自适应地最小化eA均方值，得到系统P离散域补偿器CA。继而基于自适应陷波算法对系统(1)进行隔振控制。

于是，在图2左侧蓝色线框中，构造横向滤波器结构，输出dk=s(k)+n0(k)作为目标信号，输入信号xk与n0相关，利用自适应干扰对消消去dk中干扰信号n0;而针对基频为ω0的M次谐波信号叠加于dk，则输入为

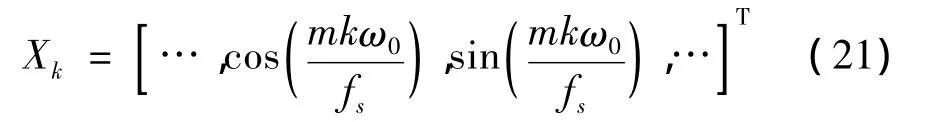
其中:fs为采样频率，m=1，2，…，M。

利用自适应干扰对消技术实现自适应陷波算法［8］，其迭代过程为

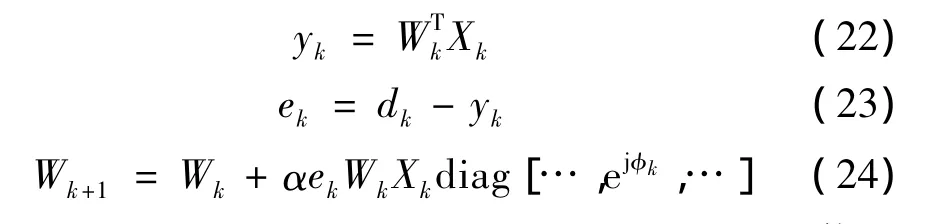
其中:diag［·］为矩阵对角函数，α 为收敛因子，ejφk为误差通道相位延迟。

3.2 参考模型

基于自适应陷波算法的主动控制环节，对于线性系统可获得理想隔振效果。然而，在自适应复合控制策略中，由于通过频域预、离散域双补偿进行非线性系统线性化，误差通道系统非线性的线性化效果，将极大影响其主动隔振效果。其中，在PCMRAIC中，参考模型是该线性化算法跟踪的目标函数，因而参考模型接近目标非线性系统的程度决定着线性化算法的收敛性、收敛速度和跟踪效果。

针对柴油机双层隔振非线性系统，在10～100 Hz频段内以间隔2 Hz进行扫频试验，获得模态试验数据。基于模态试验数据，图3和图4给出两种参考模型，并对参考模型频响函数进行数学平滑和曲线拟合建立适合自适应算法的256个权FIR模型。

在图3中，依据式(13)忽略系统非线性，基于模态试验数据估计得到线性平均后的误差通道相频特性，并假设其具有良好的幅频特性()，得到半理想半试验参考模型(简记1#参考模型)。曲线拟合与参考模型具有较好的匹配，特别在柴油机试验频段［30，60］范围内，与参考模型频域系统具有理想的匹配。

在图4中，依据式(13)忽略系统非线性，基于单频激励－响应试验数据估计系统频响函数(H∑，1)，得到2#参考模型。2#参考模型同时考虑误差通道的相频特性与幅频特性。曲线拟合，对于幅频曲线在［20，100］范围内具有好的匹配，而对于相频曲线具有一定差异且仅在［40，60］范围内具有好的匹配。

对比图3与4可见，较之1#参考模型，2#参考模型相当接近于误差通道非线性系统(PCMRAIC策略的目标系统);而在相位曲线的曲线拟合上，1#参考模型较之2#参考模型却有较好的拟合结果。因此，在柴油机双层隔振非线性系统主动控制中，需要通过比较并根据实际效果选择参考模型。

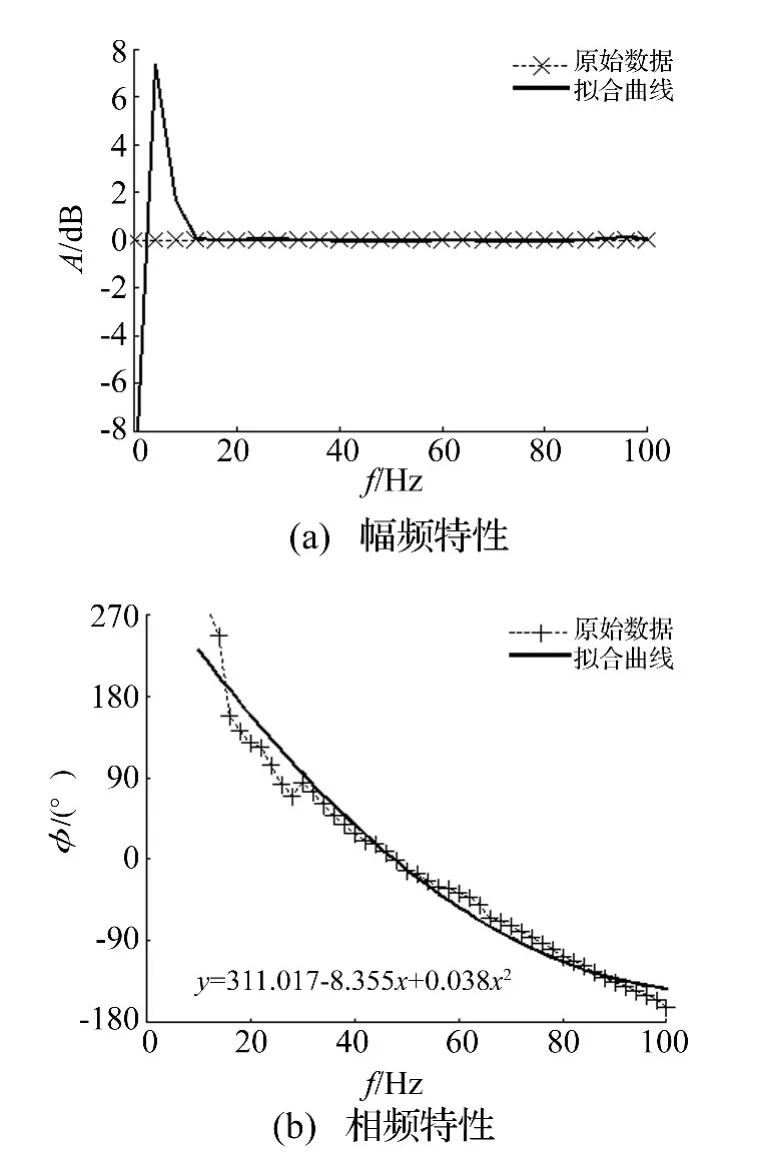
图3 1#参考模型频响曲线Fig.3 Frequency response curves of the reference Model 1

图4 2#参考模型频响曲线Fig.4 Frequency response curves of the referenceModel 2

3.3 误差通道

针对柴油机双层隔振非线性系统，采用自适应复合控制策略实现其主动隔振。由于集成自适应陷波算法，根据式(24)可知，误差通道相频特性影响自适应陷波算法的收敛性［1］，并最终决定着自适应复合控制策略的控制效果。因此，误差通道相频特性是自适应复合控制策略另一关键环节。

针对柴油机双层隔振非线性系统的主动隔振误差通道，如图5所示，给出三组相频特性曲线模型，其中:1#模型，假设误差通道为理想线性系统，利用试验获得的相频特性曲线［1］;2#模型，在误差通道为理想线性系统基于模态试验获得的相频特性曲线(H∑，1);3#模型，考虑误差通道实际非线性并在激励－响应试验数据中剔 除 H3，1、H5，1作用而辨识出的相频特性曲线(∠H1，1)［19］。由于系统存在非线性，谐频调制特性使得系统奇阶次非线性广义频响函数将作用于1阶(线性)系统响应。显然1#模型和2#模型给出的误差通道相频特性曲线包含所有阶次非线性作用，而3#模型误差通道相频特性曲线仅包含7阶及以上高阶非线性。

图5 误差通道2#通道三种相频模型曲线对比Fig.5 Phase－frequency curve comparison of three types of models employed in Path 2 of the secondary path

在图5中，对比三组误差通道相频特性，虽然各个通道具有相同变化趋势，但在相同频率点处三组相频特性曲线亦具有很大差异。1#模型和2#模型两特性曲线较平滑，且随着频率增大二者出现逐渐增大的相位差值，而在柴油机组工作频率20～65 Hz之间相位差约达到22.5～45°;3#模型相频特性曲线相对于2#模型具有相对较小的相位差，但在某些频点位置相位差仍能达到22.5°左右。可见，台架误差通道存在着非线性环节并因而对误差通道相频特性产生影响，同时台架误差通道存在着一定程度的时变特性。由于不同误差通道相频特性模型会使自适应陷波算法获得不同控制效果。因此，在柴油机双层隔振非线性系统主动控制中，需要通过比较并根据实际效果选择误差通道相频特性模型。

4 试验结果及分析

柴油机双层主动隔振非线性系统，如图1所示，通过采用四个中间质量块、四个作动器和独立控制通道等措施进行硬件去耦，耦合通道相比主通道的响应下降约为20～8 dB，误差通道近似为四个去耦通道［4，19］。因而，本文针对柴油机主动隔振非线性系统去耦误差通道 2#通道，考虑其 5阶非线性 Hammerstein模型［4，19］，在 0 ～100 Hz频段内以间隔 2 Hz 进行扫频试验，在此基础上，进行非线性系统解耦和设计自适应复合控制策略，并进行主动隔振试验及结果分析。

在主动隔振试验中，由于振动加速度响应频谱组成完全依赖于转速，并表现出包括基频谱线和一系列倍频谱线。于是，在柴油机10～25%载荷条件下，选择转 速/频 点:900/30、1055/35、1200/40、1350/45、1500/50、1650/55、1800/60 和1950/65(r·min－1/Hz)，进行主动隔振试验，试验结果如图6～9所示，其中M(i，j)为采用i#参考模型j#相频特性模型的隔振工况，最终从基频隔振效果和谐频抑制效果两方面分析自适应复合控制策略的隔振效果。

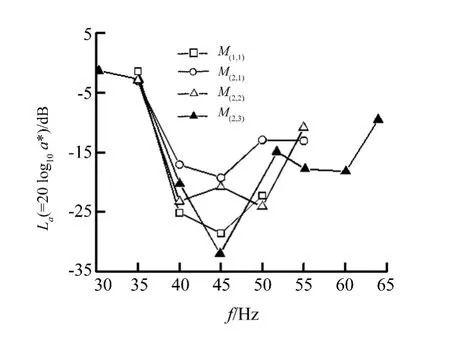
图6 试验频段误差通道2#通道基频振动消减量Fig.6 Fundamental frequency vibration decreasein Path 2 of the secondary path in test frequency range

在图6中，针对选择不同的参考模型与误差通道频响曲线，对比了自适应复合控制策略基频振动控制效果。整体上，基频振动主动控制效果较好，35 Hz以上频点上隔振量均在6 dB以上，在一些频点上隔振量甚至在20 dB以上。其中:采用M(2;3)模型，在［40，65］频段内隔振效果较理想，隔振量10 dB以上;采用M(2，1)模型，在［40，55］频段内隔振效果较理想，隔振量接近 15 dB 以上，采用 M(2，2)模型，在［40，55］频段内隔振效果较理想，隔振量10 dB以上，采用M(1，1)模型，在［40，50］频段内隔振量较理想，隔振量20 dB以上。上述结果与FIR系统参考模型相频曲线在［40，60］频段内拟合较好相对应。可见，对于基频振动控制效果，FIR系统参考模型相频曲线拟合结果，表现为显著作用。

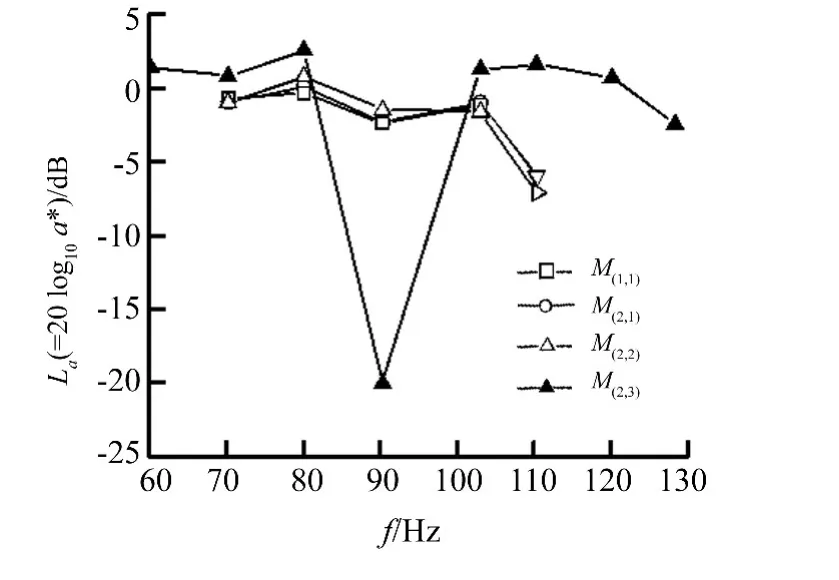
图7 试验频段误差通道2#通道2阶谐频振动消减量Fig.7 2nd－order harmonic vibration decrease in Path 2 of the secondary path in test frequency range

在图7中，针对选择不同的参考模型与误差通道频响曲线，对比了自适应复合控制策略在2阶谐频振动抑制效果。整体上，对2阶谐频振动抑制效果不好。其中:采用 M(1，1)、M(2，1)和 M(2，2)模型的主动隔振效果相似，在［35，55］频段内有一定的抑制效果;而采用M(2，3)模型仅在45 Hz有约20 dB的抑制效果，其它各频点起到了恶化效果。在 M(2，3)模型中，3#相频曲线(∠H1，1)剔除了误差通道非线性中 H3，1、H5，1作用，基频谐振广义频响函数Hn，1对误差通道相频特性影响较大。可见，对于2阶谐频振动抑制效果，基频谐振广义频响函数Hn，1对误差通道相频特性影响，表现为显著作用。

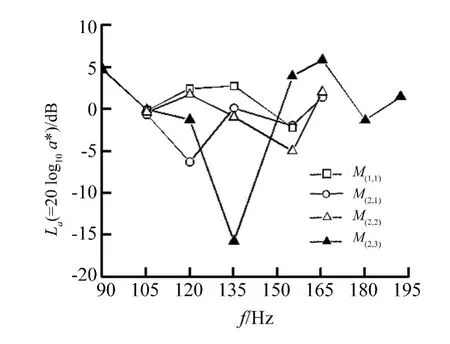
图8 试验频段误差通道2#通道3阶谐频振动消减量Fig.8 3rd－order harmonic vibration decrease in Path 2 of the secondary path in test frequency range

在图8中，针对选择不同的参考模型与误差通道频响曲线，对比了自适应复合控制策略在3阶谐频振动抑制效果。整体上，对3阶谐频振动抑制效果差异较大。其中:采用 M(1，1)模型，在［35，50］频段内抑制作用不明显，并出现略有恶化现象;采用M(2，1)模型，在［35，50］频段内得到较好的抑制作用;采用 M(2，2)模型，在［35，55］频段内抑制效果介于 M(1，1)、M(2，1)之间;采用 M(2，3)模型，除去［50，55］，在［35，65］频段内能够得到较好的抑制作用。可见，由于考虑实际幅频特征，2#参考模型较之1#参考模型，对于抑制3阶非线性更为合理;另外，通过非线性系统的CA、CP补偿，复合系统相位变化很大(参见图5)，此时3#相频曲线(∠H1，1)剔除非线性 H3，1、H5，1作用，接近于线性化后系统相位，对于抑制3阶非线性益处很大，但三组相频曲线与线性化系统相位差异亦显著影响着自适应陷波算法控制效果。

在图9中，针对选择不同的参考模型与误差通道频响曲线，综合考虑前3阶谐频振动能量，对比了自适应复合控制策略隔振效果。整体上，几种模型均获得了较好的控制效果，40 Hz以上频点上隔振量均在6 dB以上，极大地抑制系统非线性对主动控制的影响。其中，采用 M(1，1)模型，在［35，55］频段内具有一定的振动能量级消减量;采用 M(2，1)、M(2，2)模型，在［35，55］频段内振动能量级消减量大致相当，但较之M(1，1)模型的振动能量级消减量却有一定地增加;采用M(2，3)模型，除去50 Hz频点，在［35，65］频段内能够获得较理想的振动能量级消减量。可见，由于在自适应复合控制策略中集成了PCMRAIC算法，在实现非线性系统基频振动控制外，也在一定程度上抑制了系统非线性谐频振动。

针对柴油机双层隔振系统，基于系统能量建模及平均振动能量二次型函数最优下主动隔振数值分析结果［21］，图 10 给出了采用 M(2，3)模型进行的主动隔振试验结果对比分析。

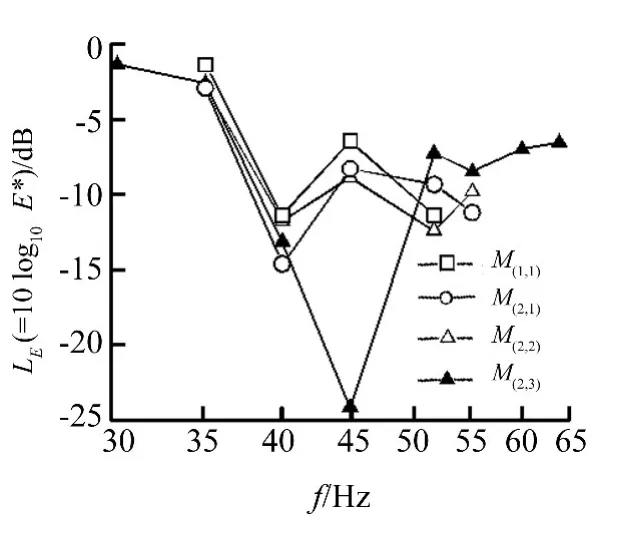
图9 试验频段误差通道2#通道前3阶谐频振动能量级消减量Fig.9 First 3 order harmonic vibration energy level decreasein Path 2 of the secondary path in test frequency range

图10 柴油机双层隔振系统能量建模与试验结果对比Fig.10 Result comparison between energy modelling andthe experiment on diesel two－stage vibration isolation system

在图10中，基于能量的观点，振动主动控制在低频段具有良好控制效果，随着控制频率升高，主动隔振效果逐步下降直至出现一个临界频率点(87.55 Hz)，而后出现控制溢出。在自适应复合控制策略中，非线性补偿器CA、CP仅通过算法补偿，未能改变振动系统结构参数，因而主动隔振效果很难优于能量建模结果。基频振动主动隔振在［40，60］频段内得到约10～30 dB隔振效果，远优于能量建模结果，系统非线性必然存在且恶化着谐频振动。而前3阶谐频振动能量级消减量在［40，60］频段内约10～20 dB，略优于能量建模结果，系统其它高阶次非线性对谐频振动恶化作用较小或相互抵消。可见，针对柴油机双层隔振非线性系统，基于自适应复合控制，通过消除系统非线性来抑制其对谐频振动影响，才能获得最优的系统振动能量级隔振效果。

5 结论

针对柴油机双层隔振系统，在主动控制中，采用四个中间质量块、作动器和独立控制通道等进行硬件去耦，也引入误差通道严重的系统非线性。在PCMRAIC频域、离散域双补偿实现误差通道非线性系统线性化基础上，集成自适应陷波算法，为去耦误差通道Hammerstein型非线性系统建立自适应复合控制策略。基于模态试验数据，借助Hammerstein型非线性系统解耦及基频广义频响函数性质，建立线性化参考模型和误差通道相频曲线模型，分析柴油双层隔振非线性系统主动隔振效果，发展自适应复合控制策略。从而得到以下结论:

(1)参考模型影响PCMRAIC的收敛性、收敛速度和跟踪能力，通过非线性系统线性化水平主导着谐频振动抑制效果。建立接近目标非线性系统的线性参考模型，利于获得好的线性化效果，也利于提供精确的误差通道相频特性。

(2)在自适应复合控制策略中，基频谐振广义频响函数对误差通道相频特性影响显著，误差通道相频曲线FIR模型拟合结果直接决定自适应陷波算法的控制效果和跟踪能力。

(3)在自适应复合控制策略中，未改变振动系统结构参数，只有通过消除系统非线性来抑制其对谐频振动影响，才能获得最优的系统振动能量级隔振效果。

然而，为提高柴油机双层隔振系统主动隔振效果，进一步需要:基于非线性系统解耦考虑5阶以上基频广义频响函数作用，提供更精确的频域预补偿器，从而建立更接近的线性参考模型;而考虑离散域补偿器慢时变性、线性化系统与参考模型接近程度、高阶非线性的存在等，提取并FIR模型拟合更为合理的误差通道相频曲线，最终发展文中建立的自适应复合控制策略。

［1］杨铁军.柴油机装置有源隔振技术研究［D］.哈尔滨:哈尔滨工程大学，2001.

［2］李维嘉，曹青松.船舶振动主动控制的研究进展与评述［J］.中国造船，2007，48(2):68－79.LI Wei－jia，CAO Qing－song.Advances and review on the research of the active control of ship vibration［J］.Shipbuilding of China，2007，48(2):68－79.

［3］王军，杨亚东，张家应，等.面向结构振动控制的压电作动器优化配置研究［J］.航空学报，2012，33(3):494－500.WANG Jun， YANG Ya－dong， ZHANG Jia－ying， et al.Investigation of piezoelectric actuator optimal configuration for structuralvibration control［J］.Acta Aeronautica et Astronautica Sinica，2012，33(3):494－500.

［4］肖斌，刘学广，刘志刚，等.柴油机隔振系统液压作动器线性化控制试验研究［J］.中国机械工程，2007，16(24):2933－2938.XIAO Bin， LIU Xue－guang， LIU Zhi－gang， et al.Experimental investigation on linearization control for hydraulic－servo actuator of diesel vibration isolation system［J］.China Mechanical Engineering，2007，16(24):2933 －2938.

［5］Natsiavas S.Steady state oscillations and stability of nonlinear dynamic vibration absorbers［J］.Journal of Sound and Vibration，1992，156(2):227 －245.

［6］聂永红，程军圣.有源噪声控制次级声源的非线性建模［J］.振动工程学报，2011，24(5):562－567.NIE Yong－hong，CHENG Jun－sheng.Non－linearity modeling of secondary sound source in active noise control［J］.Journal of Vibration Engineering，2011，24(5):562 －567.

［7］陈玉强.双层隔振系统振动主动控制技术研究［D］.哈尔滨:哈尔滨工程大学，2003.

［8］刘志刚.柴油机振动自适应有源隔离技术研究［D］哈尔滨:哈尔滨工程大学，2000.

［9］张志华.动力装置振动数值计算［M］.哈尔滨:哈尔滨工程大学出版社，2007.

［10］牛军川.基于多模型柔性隔振系统的振动机理和主动控制研究［D］.济南:山东大学，2003.

［11］杨铁军，顾仲权，刘志刚，等.双层隔振系统耦合振动主动控制试验研究［J］.振动工程学报，2003，16(2):17－20.YANG Tie－jun， GU Zhong－quan， LIU Zhi－gang， et al.Experimental research on active control of coupled vibration for a two－stage isolation system［J］.Journal of Vibration Engineering，2003，16(2):17 －20.

［12］薛福珍，柏洁.基于先验知识和神经网络的非线性建模与预测控制［J］.系统仿真学报，2004，16(5):1057－1059.XUE Fu－zhen，Bai Jie.Nonlinear modeling and predictive control based on prior knowledge and neural networks［J］.Journal of System Simulation，2004，16(5):1057－1059.

［13］Ding F，Chen T，Iwai Z.Adaptive digital control of Hammerstein nonlinear systems with limited output sampling［J］.SIAM Journal on Control and Optimization，2007，45(6):2257－2276.

［14］曹建福，韩崇昭，方洋旺.非线性系统理论及应用［M］.西安:西安交通大学出版社，2001.

［15］Bai E W.Decoupling the linear and nonlinear parts in Hammerstein model identification［J］.Automatica，2004，40(4):671－676.

［16］Crama P， Schoukens J. Hammerstein－Wiener system estimator initialization［J］.Automatica，2004，40(9):1543－1550.

［17］MäkiläP，Partington J R.On linear models for nonlinear systems［J］.Automatica，2003，39(1):1 －13.

［18］Xiao B，Gao C，Liu Z G.Decoupling analysis on nonlinear system based on the modified generalized frequency response functions［J］.Mechanical Systems and Signal Processing，2014，42(1):283 －299.

［19］肖斌，高超，李勇.基于Hammerstein模型的柴油机隔振非线性系统振动分析［J］.振动与冲击，2014，33(5):64－69.XIAO Bin，GAO Chao，LI Yong.Vibration analysis of nonlinear diesel vibration isolation system based on hammerstein model［J］.Journal of Vibration and Shock，2014，33(5):64 －69.

［20］肖斌，杨铁军，刘志刚.柴油机主动隔振液压执行器线性化控制仿真研究［J］.哈尔滨工程大学学报，2006，27(2):212－217.XIAO Bin，YANG Tie－jun，LIU Zhi－gang.Simulation of hydraulic actuator linearization control for diesel active vibration isolation system［J］.Journal of Harbin Engineering University，2006，27(2):212 －217.

［21］肖斌，李彪，夏春艳，等.基于功率流法双层隔振系统振动传递［J］.机械工程学报，2011，47(5):106－113.XIAO Bin，LI Biao，XIA Chun－yan，et al.Power flow method used to vibration transmission for two－stage vibration isolation system ［J］. Chinese Journal of Mechanical Engineering，2011，47(5):106－113.