借助几何直观教学 体悟数学基本思想
林先铭
(永泰县东门小学,福建 永泰 350700)
冯·诺依曼说过,数学思想一旦被构思出来,这门学科就开始经历它本身所特有的生命。数学思想在本质上有三个:抽象、推理、模型,被构思出来就是抽象;经历它本身所特有的生命,就是推理;能主动寻找数学内容的现实原型,主动利用数学发现现实世界中的问题,提出数学问题,并加以分析和解决,就是建模。几何直观是指利用图形描述和分析问题,把复杂的数学问题变得简明、形象。由此可见,几何直观既能帮助学生有效地解决数学问题,又能引领学生体悟数学基本思想。鉴于这种认识,笔者结合自己教学实践,谈谈如何借助几何直观来引导学生感悟蕴含其中的数学基本思想。
一、借助几何直观,让学生体悟抽象思想
抽象思想是将现实世界中的数量关系和空间形式进行适度抽象,是从异彩纷呈的事物中抽象出最具共性的本质的东西,它需要经历从感性认识到理性认识的过程。几何直观对学生理解算理,掌握算法,建构法则有不可估量的作用,为运算能力的提高奠定坚实基础。如,在教学“两位数乘两位数”时,笔者借助几何直观,来引导学生体验并感悟建构法则的逐步抽象过程。
1.创设情境。教师呈现现实情境:“双休日,小东的爸爸为了增长孩子的知识,便带小东去三元书店购买《名家文学读本》,每套12本,每本24元。”这里所提供的买书情境,为后面提出问题和列出算式做了很好的铺垫。
2.列出算式。教师先让学生读题明意,并指出获取了那些信息。接着教师引导学生根据情境,能否提出问题?学生提出“买这1套书应付多少钱?”并列出算式“24×12”“24×12=?”此时的数学问题不再是课本知识上的数学问题,而是富有生活实际意义的数学问题,是学生从感性认识到理性认识的一次飞跃。
3.以图示理。学生虽弄清了题意,学会了列式。但如何计算,还是不知所措,为让学生理清两位数乘两位数的算理,教师可引导学生观察直观模型,理清计算思路。如上述情景题,教师可以利用多媒体呈现一个每行24格,共有12行的格子图,随后,让学生观察思考:格与行之间的关系,最后让学生计算出一共有多少格。(格子图略)此格子图能形象直观地呈现24和12的关系,学生一目了然,茅塞顿开。这时,教师应趁势引导学生自主阐述,可以先算10行有多少格,再算2行有多少格,列式为24×10=240,24×2=48,240+48=288。教学到此,学生对算理已有所领悟,为下面抽象概括和理解法则起到了举足轻重的作用。
4.符号表征。教学“符号表征”这一步,教师应着力把语言表述与符号表征进行无缝对接,并互相转换。可借助已有的直观经验,用“先算什么,再算什么,最后算什么”等语言表述,来解决符号表征对应问题。此时,教师应做好两件事:一是根据学生语言表述,利用课件把计算法则逐步呈现出来;二是将学生语言表述的内容抽象成用数学符号表征的形式 (即竖式)(如下图)。

由此可见,“以图示理”是最直接、最形象的,它能让学生领悟算理;“符号表征”是最简洁、最明了的,它能让学生明白算法,抽象出法则。让学生经历“情境创设—列出算式—以图示理—符号表征”的抽象渐进过程,是让学生体会抽象思想的一种好的策略。
二、借助几何直观,让学生体悟推理思想
推理是数学的重要思维方式。置身在形态各异、色彩纷呈的现实世界中,人们会时常遇到繁杂的数学问题,但仔细一想,这些问题都有一些数量结构和几何结构蕴含其中。面对这种问题,教师可引导学生借助几何直观,把复杂的问题简单化、条理化、明晰化,让学生在观察和操作、比较和分析、抽象和概括中尝试推理,构建新知。运用假设丰富推理活动经验,用感悟推理思想,是一条好的途径。如,教学“假设应用题”时,教师引导学生经历“感知情境—借助直观—运用假设—总结规律”这一过程,以此来体悟推理思想。具体教学流程如下四步进行:
1.出示题目,感知情境,激发欲望。
教师出示“有五元、二元人民币共10张,共32元,两种钱各几张?”,让学生审题、思考、动笔计算,由于学生尚未进行推理训练,解题思路满无头绪,一片茫然,所示答案也是各自不一。

2.借助直观,引导假设,产生矛盾。教师让学生先假设10张全是2元的,随机问学生你发现了什么?学生发现了:假设结果与题中已知条件相矛盾。原题中人民币总值32元,假设后总值只有20元,少了12元。这是什么原因?如右图所示:

3.思考原因,发现问题,解决问题。教师让学生说出其中原因,并找出解决问题的办法。学生经过观察分析,找到了矛盾的原因和解决问题的办法,即:刚才假设中把其中五元的人民币都看成2元,这样每张5元人民币都少了3元,一共少了12元,算式:12÷3,就可以求出5元人民币的张数。
4.进行验证,总结规律,运用规律。教师引领学生继续探究:刚才我们是把10张人民币假设成全是2元的,现在把10张人民币假设成全是5元的,又会产生什么矛盾呢?学生通过计算发现,其结果人民币的总值比已知多了18元,那是因为把2元看成5元,每张多了3元,算式:18÷3,就可以求出2元人民币的张数。教学至此,教师让学生观察比较这两个算式,看看你们有什么发现?学生通过这两种假设比较,发现了:(1)假设都是2元时,先求出的是5元的张数;(2)假设都是5元时,先求出的是2元的张数;(3)少的总钱数÷每张少的钱数=5元人民币的张数;(4)多的总钱数÷每张多的钱数=2元人民币的张数。为了巩固深化知识,运用假设方法,让学生进行自主解决生活实际问题,教师再次出示题目:“6元1袋的的白砂糖和10元1袋的白砂糖共10袋,共用去68元。那么这两种白砂糖各有多少袋?”通过这一训练,促使学生知其然并知其所以然。
由此可见,教学中,通过图案或图形,对情境描述的量进行假设,促进学生直观、有序地进行数学思考,找准问题穴点,疏通解题思路,掌握推理方法,长此训练,就能提高学生的推理能力。
三、借助几何直观,让学生体悟建模思想
数学模型是联系数学与现实世界的桥梁。数学建模就是建立数学模型的过程,即“情境体验——图示理解——建立模型——应用模型”的过程,让学生获得数学建模的直接经验和体验,进而逐步体会、感悟建模思想。几何直观对于数学问题的分析,具有“一画胜百言”的作用,如教学《相遇行程应用题》时,笔者是这样展开教学的:
1.情境体验。教师创设情境引导学生实施:(1)三组动画演示。具体演示内容:①两车同时从甲乙两地出发,相向而行,X秒后相遇;②两车同时从一个地点相背而行,X秒后到达两地;③甲车从一地先行,乙车后行,再经过X秒后相遇。(2)带问题观察、思考。教师要求学生仔细观察两车运动的情况,让学生思考两车的出发地点、时间、方向、结果的变化情况。
2.图示理解。教师引导学生在充分观察、思考、交流、尝试的基础上,将实践体验的众多信息用线段图形式描绘出来,图示情况如下:
(1)甲乙同时从两地出发,相向而行,结果相遇。
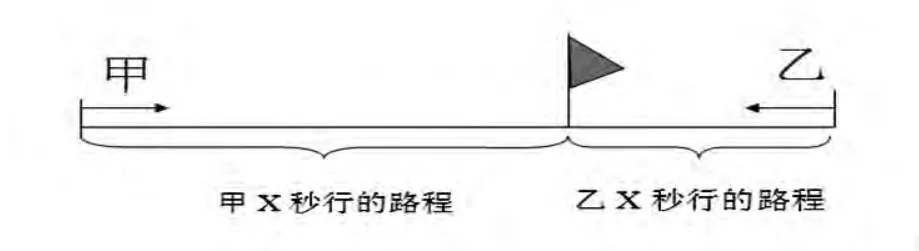
(2)甲乙同时同地相背而行,X秒后到达AB两地。
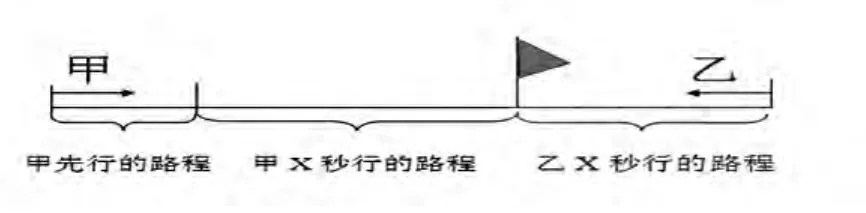
(3)甲乙从两地出发,甲先行,乙后行,结果相遇。
纵观上图,学生通过画线段图,直观的呈现相遇行程问题的模型,足见学生对如何解决此类问题有个初步的认识。
3.建立模型。教师引导学生利用上面线段图,找出等量关系式:①从两地同时出发,相向而行,所用时间相同,即:甲行的路程+乙行的路程=全程;②同时同地相背而行,所用时间相同,即:甲行的路程+乙行的路程=全程;③从两地出发,甲先行,乙后行,相向而行,所用时间不同,即:甲先行的路程+甲后行的路程+乙行的路程=全程。
4.应用模型:为了深化和拓展所学知识,教师趁势让学生选择以下所呈现的信息,编成相遇问题的应用题,再自主列式解答:①小虎和小丽同时从两地出发相向而行;②小华每分钟走50米;③经过6分钟两人相遇;④两地相距540米;⑤小虎每分钟走55米。
从上面教学过程可以看出,引导学生建构数学模型,让学生体悟数学思想,教师要充分利用情境体验,运用直观图形,构建起相应的数量关系模型,从而利用模型解决实际问题,在应用模型的过程中不断完善对已建立的数学模型的理解,有助于提高学生发现数学、“创造”数学、运用数学的数学素养。
[1]教育部.义务教育数学课程标准(2011年版)[S].北京:北京师范大学出版社,2012.
[2]史宁中.数学思想概论[J].小学数学(数学版),2013(3).

