多轴车辆测功试验台多电机转速同步控制方法研究

杨 勇，周晓军，刘晨曦，陈道泉，李由力

(浙江大学 流体动力与机电系统国家重点实验室，杭州 310027)

随着汽车工业的发展，多轴驱动车辆应用愈加广泛。为更好测试多轴驱动车辆性能，需对多轴测功试验台进行研究。在多轴测功试验台上进行车辆试验时，传动系统由发动机驱动，各测功电机模拟车辆负载。对试验台控制系统而言，当电机施加负载时，系统控制及车辆试验精度会受各电机间转速同步性能影响。电机间转速同步性越好上述精度越高。因此，必须保证加载电机间转速的同步性［1－2］。

车辆的传动系统通过不同机械元件实现每个车轮的动力分配。传动系统存在差速器时，欲在试验时保持各电机转速同步，需使电机据车辆动力分配进行加载。此外，引起电机转速不同步的原因主要有:①电机、齿轮箱、变频器等机械、电子器件均存在离散性。即使元器件标称参数相同，其真实参数及性能也不可能完全相同。因此各电机在目标载荷设定值符合车辆动力分配要求情况下，实际施加的负载不可能完全与车辆动力分配要求一致。因此会导致各电机间转速不同步。②测功电机接入传动系统后，使各电机的动力学模型之间存在一定程度的相互耦合。使某个电机的动力学特性受其它电机影响。因此即使各电机实际施加的负载完全符合车辆动力分配要求，因存在耦合，也可能导致各电机间转速不同步。任何多轴车辆测功试验系统均存在上述问题，且较难消除。欲提高多轴测功试验台电机间转速的同步性能，除需使电机按车辆动力分配要求加载外，尚须对整个系统进行模型分析，并设计控制算法解决转速同步问题。

本文对车辆传动系统中常见的机械元件进行理想化建模，发现通过组合形成多轴车辆试验台理想化动力学模型。传动系统中存在足够数量的轴间行星齿轮差速器及轮间行星齿轮差速器时每个电机的理想动力学模型是独立的，不受车辆传动系统耦合影响。据差速反馈思想，提出多电机加载时的转速同步控制策略，以保证多电机加载时转速的同步性能。

1 多电机加载系统理想动力学建模

多轴试验台测控系统控制对象是由多个测功电机与车辆传动系统通过万向联轴器连成机械传动系统。建立多轴试验台多电机加载系统理想动态模型时需综合不同类型机械传动元件的动力学特性，忽略传动系统自身的摩擦、阻尼影响及机械惯量。不同类型机械传动元件的输入、输出端之间存在不同的动力学关系［3－4］。

1.1 传动轴

扭矩通过传动轴传递，忽略传动轴惯量，其动力学关系为

式中:Min为传动轴输入力矩;Mout为输出力矩。

1.2 变速箱

常用变速箱多为齿轮传动，在传动比确定情况下变速箱各端动力学关系为

式中:Min为变速箱输入力矩;ωin为输入转速;Mout为输出力矩;ωout为输出转速;ηg为传动比。

1.3 连接测功电机的驱动桥

常见驱动桥中存在轮间差速器，且为对称式行星齿轮差速器，因此连接测功电机的驱动桥各端动力学关系为

式中:M1，M2为驱动桥两端电机扭矩;ω1，ω2为两端电机转速;I1，I2为两端电机转动惯量;Min为输入力矩;ωin为输入转速;ηd为传动比。

1.4 连接测功电机的贯通桥

常见贯通桥中有轮间差速器、轴间差速器各一。前者为对称式行星齿轮差速器，后者则据车辆扭矩分配需要为对称式或非对称式行星齿轮差速器。因此连接测功电机的贯通桥各端动力学关系为

式中:M1，M2为贯通桥两端电机扭矩;ω1，ω2为两端电机转速;I1，I2为两端电机转动惯量;Min为输入力矩;ωin为输入转速;Mout为输出力矩;ωout为输出转速;ηp为传动比;αp为轴间差速器特征参数。

1.5 分动器

常用分动器中存在轴间差速器，并据车辆扭矩分配需要为对称式或非对称式行星齿轮差速器。因此分动器各端动力学关系为

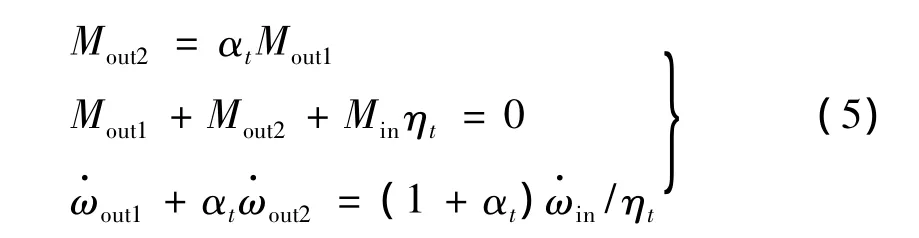
式中:Min为分动器输入力矩;ωin为输入转速;Mout1为前轴输出力矩;ωout1为前轴输出转速;Mout2为后轴输出力矩;ωout2为后轴输出转速;ηt为传动比，αt为轴间差速器特征参数。

1.6 测功试验台动力学模型

为获得整车多电机加载理想动态模型，据实际车辆传动系统需要，选各种机械转动元件的动力学关系联立组成完整的多电机系统动力学关系，写成矩阵形式为

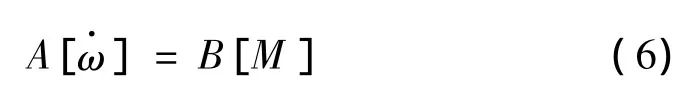
可得多电机加载系统理想动力学模型为

以三轴驱动车辆为例，试验台布局见图1。

图1 三轴驱动车辆测功试验台布局Fig.1 Dynamometer test bench's stand layout of three-axles driving vehicle

车辆分动器前输出动力至轴1、轴2，后输出动力至轴3。且驱动桥传动比ηd与贯通桥传动比ηd相等，即ηd=ηp=η。据式(1)～式(5)，联立并化简得

据式(7)、(8)可得多电机加载系统理想动力学模型为

式中:M0为发动机驱动扭矩;ω0为发动机转速;Mij为各电机施加负载;ωij为各电机转速;Iij为各电机系统惯量，其中i表示驱动轴，j表示驱动轴两侧车轮。

由式(9)看出，差速器特征参数如αp，αt等仅对各电机所受驱动力矩大小产生影响。虽测功电机模型被车辆传动系统耦合，但由于存在足够多的轮间行星齿轮、轴间行星齿轮差速器，使单个电机控制模型仍为原自身的动力学模型，不受其它电机模型影响。整体试验台系统模型较简单。

特别指出，常见车辆传动系统进行动力分配时，多采用动力平均分配原则。对图1的三轴车辆，动力平均分配时，轴2的贯通桥中轴间差速器特征参数αp=1，分动器中轴间差速器特征参数αt=0.5。此时该加载系统理想动力学模型简化为

2 基于差速反馈的同步控制策略

多电机同步控制多采用主从控制及耦合控制两种结构［5－7］。其中主从控制将前一电机的控制结果作为后一电机的控制命令，该结构稳态控制效果好，但动态控制效果差，且电机间存在滞后性。耦合控制通过反馈各电机的控制结果，据特定补偿规律对各电机控制命令进行修正，以实现同步控制。耦合控制动态控制效果好，但需据不同控制对象提出不同补偿规律。较主从控制，耦合控制更适合测功试验台多电机加载时转速同步控制。本文基于耦合控制原理，提出适用于多轴车辆测功试验台的差速反馈同步控制策略。

由于多轴车辆试验台的被控对象为测功电机与车辆传动系统连接组成的综合机械传动系统，因此控制目标应与车辆实际运行状态相符。定义同轴轮间转速误差为ei=ωi1－ωi2，定义不同轴间转速误差为εi=∑ωij/2 － ∑ωi+1，j/2

试验台控制系统控制目的使车辆各车轮速度保持一致。即ei→0，εi→0。故对电机基础加载信号uij进行补偿时，应包含电机所在轴的轮间转速误差ei的信息及相邻两轴间转速误差 εi－1，εi的信息。

据差速反馈补偿同步控制思想，考虑各电机基础加载信号不相同情况，定义补偿后的电机加载信号为

式中:Ci为轮间控制器;Di为轴间控制器，多采用PI控制器。

以u'i1为例，补偿后的电机加载信号由3部分组成:

(1)基础加载信号ui1。

(3)通过轮间转速误差ei进行的轮间补偿为，其中为轮间载荷不同时加权系数。

对图1三轴驱动车辆，当采用动力平均分配原则时，据所得加载系统理想化模型及差速反馈控制策略得测功系统控制框图见图2。由于采用动力平均分配原则，因此为保证车辆加载时转速同步性，要求图2中各电机基础加载信号相同，即uij=u。对其它因素所致转速不同步，则由系统通过同步控制算法消除。

图2 系统控制图Fig.2 Control diagram of dynamometer system

3 仿真验证

据所建三轴车辆试验台动力学模型及差速反馈补偿的同步控制策略，通过Matlab的Simulink模块对控制系统进行仿真验证。为使仿真更接近实际，考虑机械、电器设备的离散性及各电机模型、变频器扭矩响应模型不能完全相同，但模型间差别应较小，仿真时令轴间控制器Di、轮间控制器Ci参数相同，均为PI控制器，比例系数为Kp，积分时间为Ti。仿真条件见表1。

表1 仿真条件Tab.1 Simulation conditions

仿真结果见图3。由图3看出，当仿真时间0≤t＜7 s时控制发动机转速ω0=1300 r/min;7≤t＜12 s时控制发动机转速ω0=1800 r/min。各电机加载及同步控制开始时间为t=3 s。图3(a)～(c)的仿真结果为只考虑电机惯量不同时对系统转速同步性影响及控制算法的控制效果(电机惯量Iij见表1，且τij=0，kij=1)。由图3(a)无同步控制仿真结果看出，各转速误差随发动机转速增大而增大，加载时间长短对转速误差无影响;由图3(b)单独比例控制仿真结果看出，比例控制能较好消除由电机惯量不同引起的转速不同步;由图3(c)比例－积分控制仿真结果知，虽亦能消除转速误差，但由于加入积分控制引起转速误差震荡而致误差收敛时间延长。

图3(d)～(f)的仿真结果为只考虑扭矩响应时间不同时对系统转速同步性影响及控制算法的控制效果(扭矩响应时间 τij见表1，且 Iij=10，kij=1)。由图3(d)无同步控制仿真结果看出，各转速误差不受发动机转速及加载时间影响，仅与扭矩响应时间有关;由图3(e)单独比例控制仿真结果知，比例控制能较好消除由扭矩响应时间不同引起的转速不同步;由图3(f)比例－积分控制仿真结果知，虽亦能消除转速误差，但由于加入积分控制，引起转速误差震荡，致误差收敛时间延长。

图3 仿真结果Fig.3 Result of simulation

图3(g)～(i)的仿真结果只考虑扭矩增益不同时对系统转速同步性影响及控制算法的控制效果(扭矩增益kij见表1，且Iij=10，τij=0)。由图3(g)无同步控制仿真结果看出，各转速误差不受发动机转速影响，但受加载时间影响，加载时间越长误差越大;由图3(h)单独比例控制仿真结果可知，比例控制不能完全消除由扭矩增益不同引起的转速不同步，存在稳态误差;由图3(i)比例－积分控制仿真结果知，由于加入积分控制，消除稳态误差，使各转速误差得到收敛。

在实际试验系统中引起转速不同步因素均存在。图3(j)～(l)的仿真结果为考虑三种因素全部不同时对系统转速同步性影响及控制算法的控制效果(电机惯量Iij、扭矩响应时间τij、扭矩增益kij均见表1)。由图3(j)无同步控制仿真结果看出，转速误差既受发动机转速影响又受加载时间影响，为多种因素共同作用结果;由图3(k)单独比例控制仿真结果可知，比例控制不能完全消除稳态误差;由图3(l)比例－积分控制仿真结果知，由于加入积分控制消除稳态误差，使各转速误差得到收敛。因此在设计控制策略的轴间、轮间控制器时采用比例－积分控制，才能更好地保证系统加载电机转速的同步性。

4 结论

(1)本文针对多轴测功试验台进行整车试验时如何保证各电机转速的同步性进行研究，并分析测功系统中可能导致电机转速不同步原因。通过对系统进行理想化建模，发现在一定条件下系统模型可视为由独立的电机模型组成，不受多轴车辆传动系统耦合影响。

(2)据所建模型，提出的基于差速反馈的多电机同步控制策略，可实现多轴车辆试验时电机转速同步控制，并通过计算机仿真，验证该同步控制策略可获得较好控制效果。

［1］陈庆伟，郭毓，胡维礼，等.多电机同步联动系统的动力学分析与建模［J］.东南大学学报，2004，34:135 －140.CHEN Qing-wei，GUO Yu，HU Wei-li，et al.Dynamics analysis and modeling of multi-motor synchronized driving system［J］.Joutral of Southeast University，2004，34:135－140.

［2］张今朝，刘国海，潘天红.多电机同步系统的多模型辨识［J］.电机与控制学报，2009，13(1):138 －142.ZHANG Jin-zhao，LIU Guo-hai，PAN Tian-hong.Multi-model identification to multi-motor synchronous system［J］.Electric Machines and Control，2009，13(1):138 －142.

［3］金娇娇.车辆分动器性能及其检测系统研究［D］.杭州:浙江大学，2008.

［4］张利鹏，祁炳楠.对称式行星齿轮差速器的转矩转速分配特性研究［J］.机械设计与制造，2012，9:138 －140.ZHANG Li-peng，QI Bing-nan.Torque and speed distribution characteristic of symmetrical planetary gear differential［J］.Machinery Design＆ Manufacture，2012，9:138－140.

［5］张承慧，石庆升，程金.一种基于相邻耦合误差的多电机同步控制策略［J］.中国电机工程学报，2007，25(15):59－63.ZHANG Cheng-hui，SHI Qing-sheng，CHENG Jin.Synchronization control strategy in multi-motor systems based on the adjacent coupling error［J］.China Electrical Engineering Journal，2007，25(15):59 －63.

［6］Zhao D Z，Li C W，Ren J.Speed synchronization of multiple induction motors with adjacent cross-coupling control［J］.IET Control Theory and Applications，2010，4(1):119 －128.

［7］Lin F J，Hsieh H J，Chou P H.Digital signal processor-based cross-coupled synchronous control of dual linear motors via functional link radial basis function network［J］.IET Control Theory and Applications，2011，5(4):552－564.