微创食管缝合器的运动学与动力学分析研究

程云章，谭启路，宋成立，徐兆红

上海理工大学医疗器械与食品学院(上海，200093)

广告

微创食管缝合器的运动学与动力学分析研究

程云章，谭启路，宋成立，徐兆红

上海理工大学医疗器械与食品学院(上海，200093)

提出了一种新型的应用于食管空肠吻合术的微创食管缝合器的机械结构，并应用D-H坐标系法和基于旋量理论的Kane方程分别进行了运动学仿真和动力学分析。运动学仿真表明，微创食管缝合器定夹钳在初始状态和定位状态之间时，具有一个自由度，满足机构运动的条件。动力学分析表明，为保证微创食管缝合器的运动平稳，驱动力能够满足临床力学传递要求。

微创食管吻合器;多自由度器械;运动学;动力学

0 引言

肿瘤疾病、心脑血管疾病和糖尿病，已成为人类健康的三大杀手，其中肿瘤疾病以各种癌症的发病率为最高。而对于癌症，依次以肺癌、胃癌、肠癌的死亡率最为显著。有研究显示［1］，与世界各国比较，中国男性、女性的胃癌死亡率位居世界首位。从近20年的统计数据来看，胃癌死亡率在30～59岁年龄段内呈下降趋势，60岁以上年龄段呈上升趋势，但是总的来看呈上升趋势，因而人口老化是胃癌死亡率上升的重要因素。于是，胃癌的治疗则显得尤为重要，而外科手术是胃癌治疗的主要治疗方法。患者在进行胃切除术之后，为了保持消化道的完整，还需要进行相应的吻合术。其中，食管空肠吻合术是一种比较常用的吻合术。

食管空肠吻合术是用在全胃切除术之后，将食管末端与空肠部分进行拼接吻合的一种微创外科手术［2-5］。美国外科公司和爱惜康公司生产的管状吻合器有重复使用的不锈钢吻合器和一次性使用的吻合器。临床上多使用一次性吻合器，其优点是做工精致，对合好，内径较大，可减少吻合口狭窄的发生，但价格较贵。

国产胃肠吻合器主要有三种［6］:(1)GF-1型管状吻合器，用于吻合的组件成圆环形，为全层内翻式吻合;(2)XF残端直线缝合器，用于缝合关闭胃肠道的残端，为全层外翻式缝合;(3)CF-1侧侧吻合器，采用订书机的原理，捏拢锁柄时，将组织对合固定。

为了便于微创手术下的胃肠吻合，本文研究的食管缝合器既要具有传统吻合器夹取食管壁并穿线缝合的功能，又要能够灵活地穿过患者腹部的手术切口并对手术部位进行操作，对日后微创医疗器械的研发具有重要的临床意义。

1 微创食管缝合器的机械结构

微创手术中，患者的腹腔所开的切口直径在10 mm左右，所以相应的手术器械的工作部分最大直径也必须接近这个数值。此外，微创手术中人体腹腔内操作空间有限、腹腔镜视野狭窄，如果单靠医生徒手控制钳杆部分来调整方向，手术将很难顺利进行，所以吻合器的工作部分还需要灵活。而且，夹取食管时，吻合器的两块钳爪不希望有角度，否则容易破坏组织。因此，减小吻合器缝合头的最大直径、增加其自由度、并实现两钳爪的平行开合，是微创食管缝合器的主要特征，其机械结构如图1所示。

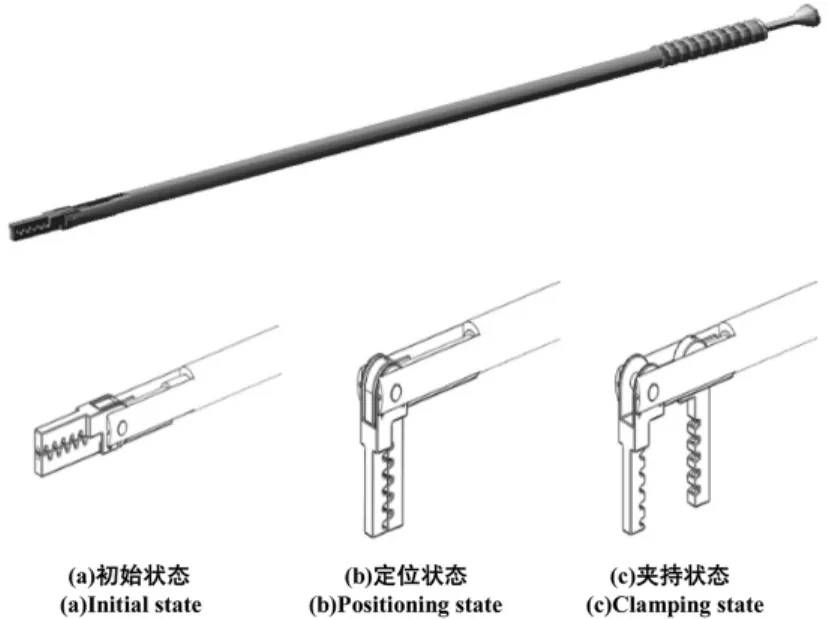
图1 微创食管缝合器的机械机构Fig.1 M echanical structure of the esophageal purse-string suture instrument

微创食管缝合器的初始状态如图1(a)所示，其操作部分分为旋转推杆和开合推杆，旋转推杆控制缝合头动夹钳和定夹钳的旋转运动，而开合推杆控制动夹钳的水平运动;其在工作状态下的定位状态如图1(b)所示，夹持状态如图1(c)所示。微创食管缝合器的工作原理分为两部分——缝合头的旋转和动夹钳的开合。向后拖动旋转推杆，带动固定在连接臂末端的活动销，使得活动销向后作水平运动。这一运动可分解为沿槽方向的滑动和垂直于槽方向的瞬时切向运动，其中后者提供了定夹钳的旋转动力。当缝合头旋转至竖直位置处时，保持旋转推杆不动以使得缝合头固定。此时向后拉动开合推杆，保持夹持的能力。在手术中灵活地调节夹钳间距来实现夹持缝合的功能。

2 微创食管吻合器的运动学分析

本文采用Denavit-Hartenberg(D-H)法，分析了从动件缝合头在驱动作用下，其旋转角度和角速度随时间的变化关系。

2.1 D-H坐标系

D-H坐标系是进行机械结构运动学分析的惯用坐标系。该坐标系的规定如下:在结构的各主要构件上固定有坐标系，其Z轴与运动副轴线重合，X轴沿着相邻两Z轴的公垂线，Y轴由右手坐标系法则确定［7］。D-H坐标系由4个参数来确定:

2.2 运动学方程的建立与求解

图2 缝合头Fig.2 Suture portion

实验中，驱动件旋转推杆的平动速度v的加速度设定为1 m/s，相关文献表明，这一加速度符合人手在正常情况下的移动状态，驱动件总位移设定为9mm。手在正常情况下的移动状态，驱动件总位移设定为9 mm。图2(a)为目标构件的示意图，驱动件是连接于旋转推杆末端的连接架，图2(b)为其等效的机构运动简图。为了真实模拟手术时器械的工作情况，将重力的方向定义为旋转推杆中轴线的方向。

图2(b)中，将驱动件和工作部件简化为刚性杆件，将销轴滑槽部分等效为一个滑动副和一个旋转副。为了分析方便，此处将二者分开一定距离。实际上，l2=0，坐标系O2X2Y2Z2与O3X3Y3Z3在原点处重合。

根据平面机构自由度计算公式

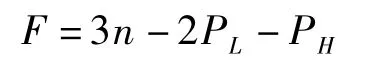
可以得出，所研究的机构自由度F=1，而驱动件个数为1，因此该机构的运动是确定的。其相邻坐标参数如表1所示。

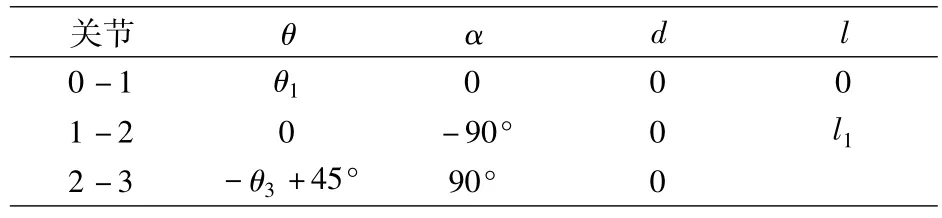
表1 相邻坐标参数Tab.1 Adjacent coordinate parameter

实际上，在图2(b)中，θ3=-θ1。根据串联机构的速度表达式，有［8］:

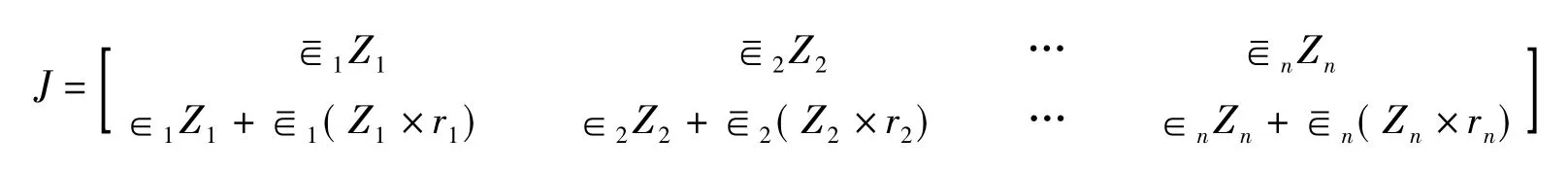
为速度雅可比矩阵。

为了求出速度雅可比矩阵，需要求出两相邻关节间坐标变换矩阵。根据坐标间的变换关系［8］，求解出各关节相对于基坐标系的坐标变换矩阵，将各坐标系变换到基坐标系中，得:

根据各个关节的类型，确定各个关节的关节变量，从而确定关节速度矢量，最后求解速度雅可比矩阵如下:

将(2)式中的速度雅可比矩阵带回(1)式中，可以求得驱动件的运动旋量，即:

本文中，驱动件的速度v是时间的函数，即v= v(t)，且行程L=9 mm，通过(3)式，可以反解出在食管缝合器缝合头旋转过程和驱动件移动过程中的θ1-t、θ·1-t和l-t、v-t关系。根据求解过程做了仿真，结果分别如图3、图4、图5和图6所示。

图3 缝合头旋转角度与时间的关系曲线Fig.3 Relation curve of rotation angle and time of the suture portion

图3为缝合头旋转角度随时间的变化关系曲线图(θ1-t图线)。缝合头旋转角度与时间的函数关系单调增加，整个运行时间持续0.425 s。

图4 缝合头旋转角速度与时间的关系曲线Fig.4 Relation curve of rotation angular velocity and time of the suture portion

图4为缝合头旋转角速度随时间的变化关系曲线图(θ·1-t图线)。缝合头旋转角速度与时间的函数关系为先增加后减少，在0.425 s运动终点时突变为零。经测定在0.33 s时达到最大值，为402.4°/s。

图5 驱动件位移与时间的关系曲线Fig.5 Relation curve of displacement and time of the driver

图5为驱动件位移随时间的变化关系曲线图(l -t图线)。驱动件位移与时间的函数关系同缝合头旋转角度与时间的函数关系相类似。由此说明，驱动件与缝合头的运动保持高度的一致性，整个过程运动平稳。

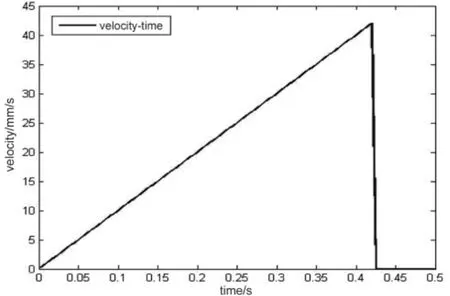
图6 驱动件速度与时间的关系曲线Fig.6 Relation curve of velocity and time of the driver

图6为驱动件速度随时间的变化关系曲线图(v -t图线)。驱动件速度与时间的函数关系呈线性增长趋势，这与驱动速度的定义形式是吻合的。经测定其所能达到的最大速度为42 mm/s。

仿真结果表明，人手在正常移动状态下对旋转推杆拉动时，缝合头旋转运动的稳定性符合器械的临床要求。

3 微创食管吻合器的动力学分析

在动力学分析部分，本文结合了旋量理论和Kane动力学方程，分析了工作部件(缝合头)在驱动作用下，驱动力随时间的变化关系。

3.1 串联机构基于旋量理论的Kane动力学方程［9］

Kane方程的一般表达式为

其中Fj为广义主动力，为广义惯性力。结合上述关节运动旋量坐标的表达形式，得到串联机构基于旋量理论的Kane动力学方程为

式(5)中RCi和MCi为第i个连杆上将主动力向质心C简化所得的主矢和主矩，和为其上惯性力向质心C简化所得的主矢和主矩，为相对于第i连杆坐标系的第j个瞬时关节运动旋量坐标。

3.2 动力学方程的建立与求解

图7所示为缝合头各关节连接示意图。

图7 缝合头关节连接Fig.7 Joints of the suture portion

当关节1旋转角度θ1后，可以求得q1在Li物体坐标系中的坐标及运动旋量方向q1和ω1，之后得到第1个连杆相对于各关节的运动旋量坐标和，最后，求得连杆L1的物体雅可比矩阵为

当关节2旋转角度θ2后，同理可求得连杆L2的物体雅可比矩阵为

与运动学分析一样，本文根据求解过程分别对动夹钳-连接板旋转副和销轴滑槽副做了仿真，结果如图8、图9所示。

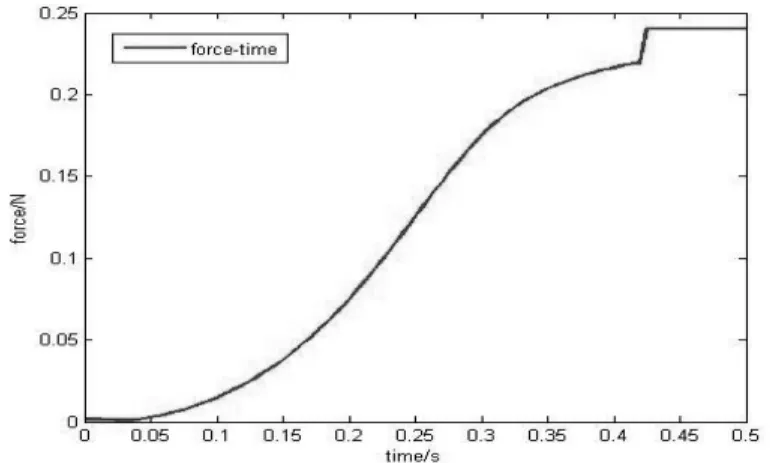
图8 动夹钳-连接板旋转副支反力与时间的关系曲线Fig.8 Relation curve of counterforces and time of the revolute between mobile clip and connection plates

图9 销轴滑槽副驱动力与时间的关系曲线Fig.9 Relation curve of driving forces and time of the sliding pair between pins and chutes

由图8可知，动夹钳-连接板旋转副支反力与时间的函数关系为单调增加，在0.425 s运动终点时达到最大值，为0.240 1 N。由图9可知，销轴滑槽副驱动力与时间的函数关系较为复杂，其大致趋势为先增加后减小，在0.34 s时达到最大值为0.172 6 N，但在0.3 s时刻存在一个突变。此外，实验另测得整个旋转过程中，两个连接板与动夹钳所形成的动夹钳-连接板旋转副对动夹钳的支反力，和连接架上的两接杆末端对定夹钳两侧的驱动力是完全相同的，证明在运动过程中定夹钳并无偏心拉伸的现象。由此，进一步说明了之前的运动学分析过程中缝合头旋转运动的平稳性，其力学性能满足临床力学传递要求。

4 结论

本文以微创手术——食管空肠吻合术为例，对其所需要的手术器械——微创食管吻合器进行了机械结构的创新，并对其进行了一系列运动学与动力学分析，最后对其旋转过程中旋转角度、角速度、驱动力大小与时间的关系做了研究，由此对其运动的稳定性做了一个评估，其结果均符合临床要求。

［1］孙秀娣，牧人，周有尚，等.中国胃癌死亡率20年变化情况分析及其发展趋势预测［J］.中华肿瘤杂志，2004，26(1):4-9.

［2］吴学豪，郭安全，黎介寿，等.应用吻合器行食管空肠吻合术［J］.江苏医药，1989，10:003.

［3］Kim H I，Cho I，Jang D S，etal.Intracorporeal esophagojejunostomy using a circular stapler with a new pursestring suture technique during laparoscopic total gastrectomy［J］.JAm Coll Surgeons，2013，216(2):e11-e16.

［4］Yoshikawa T，Hayashi T，Aoyama T，et al.Laparoscopic esophagojejunostomy using the EndoStitch and a circular stapler under a direct view created by the ENDOCAMELEON［J］.Gastric Cancer，2013，16(4):609-614.

［5］Miyoshi K，Fuchimoto S，Ohsaki T，et al.Suture line recurrence in jejunal pouch replaced after total gastrectomy for gastric cancer［J］.Gastric Cancer，1999，2(3):194 -197.

［6］于跃明，王贵英.结直肠癌［M］.北京:科学技术文献出版社.2010.

［7］牛元会，程光明，杨志刚.DH坐标系下机械手正向运动学分析［J］.机械工程师，2006(7):27-29.

［8］(加拿大)Jorge Angeles著，宋伟刚译.机器人机械系统原理理论、方法和算法［M］.北京:机械工业出版社.2004.

［9］刘武发，龚振邦，汪勤悫.基于旋量理论的开链机器人动力学Kane方程研究［J］.应用数学和力学，2005，26 (5):577-584.

Analysis of K inematics and Dynam ics for Esophageal Purse-string Suture Instrument in M inimal Invasive Surgery

CHENG Yunzhang，TAN Qilu，SONG Chengli，XU Zhaohong
School of Medical Instrument and Food Engineering，University of Shanghai for Science and Technology(Shanghai，200093)

We proposed a structure of a new type of esophageal purse-string suture instrumentwith the application in aminimal invasive surgery(MIS)called esophagojejunostomy.In addition，we performed kinematic simulation and dynamics analysiswith D-H coordinate and Kane's equation based on the screw theory.According to the kinematic simulation，the esophageal purse-string suture instrument has one degree of freedom(DOF) when the fixed clip lies between initial state and positioning state，which satisfies the conditions ofmechanism motion.According to the dynamic analysis，for smooth movement of this esophageal purse-string suture instrument，the driving forcemeets the demands in terms of clinicalmechanics.

esophageal purse-string suture instrument，instrument ofmultiple degrees of freedom(MDOF)，kinematics，dynamics

TH777

A

1674-1242(2015)03-0127-06

10.3969/j.issn.1674-1242.2015.03.001

2015-05-30)

程云章，E-mail:cyz2008@usst.edu.cn