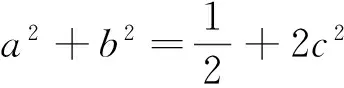重视教材例习题处理培养学生思维品质
林永晖
(福建永春县教育局,福建 泉州 362600)
重视教材例习题处理培养学生思维品质
林永晖
(福建永春县教育局,福建 泉州 362600)
例、习题的教学是整个数学教学活动的重要部分。在教学过程中重视课本例、习题的剖析教学,对典型的例题、习题进行适当的变式与延伸,可以激发学生的学习兴趣,拓展学生的解题思路,有利于培养学生良好的思维品质。
例、习题;独创性;深刻性;系统性;思维品质
教材中的例、习题体现课标要求,蕴寓知识要点,深遂而经典,具有良好的示范作用。在课堂教学中,教师若能对教材中典型的例、习题进行适当的变式与延伸,可以激发学生的学习兴趣,拓展学生的解题思路,有利于培养学生良好的思维品质。本文结合自己多年来的教学实践,从例、习题的教学中,如何培养学生思维的广阔性、独创性、深刻性、系统性、灵活性等方面谈几点看法。
1 创设问题情境,培养学生思维的广阔性
创设良好的问题情境有利于激发学生的学习兴趣、调动学生的学习积极性,让学生在问题情境中主动思考和探究[1]。在教学中,鼓励学生大胆猜想并提出问题,让学生在解决问题的求知欲驱使下,完成问题的解决过程,达到培养学生思维广阔性的目的。
例1: 解下列方程组

第一,凭直觉猜测:各方程组中可能存在某种联系。仔细观察以上各个方程的未知数系数及常数项的关系:

第二,启发学生作逆向猜测:
可以证明,逆命题也成立。
再进一步,作发散性猜想:
是否还存在某一类方程组,它们也具有一个相同的解呢?(或它们的解带有某种规律),于是将学生思维导入“实验(观察、分析)―猜想―证明”这一重要的思考问题的方法上,及时拓展学生思维层面,促进学生创造性的思维。
现将学生得出的猜测举例如下:
思维的广阔性是思维品质的一部分。培养学生思维的广阔性,必须有丰富的广阔知识面,善于从多角度、多方位、多层次去思考问题,认识问题和解决问题。教学中应注意发挥横向思维的作用,并适时的进行归纳总结。广阔的知识面和娴熟的演绎推理及归纳总结能力是提高思维的广阔性的关键。
2 探究合作互动,培养学生思维的独创性
探究合作互动是在创设教学情境的基础上,重视探究问题的提出,让学生主动参与探究的过程。这就要求教师不断提高自己的专业知识水平,在教学过程中能提出自己独到的见解,让学生有自主学习的时间和空间,提高学生的独创能力。
例2:已知P为正方形ABCD内一点,且∠PCD=∠PDC=15°,求证:△PAB是一个正三角形。
这是一道典型的习题,证法很多,如果我们巧妙地利用一个十分简单的结论:1周角等于3600来证,则其证法非常简洁,令人耳目一新。
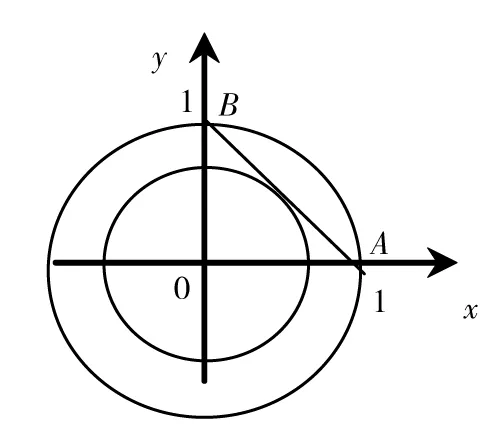
证:显然△PAD≅△PBC所以PA=PB。假设AB>PA,则∠APB>∠PBA= ∠PAB,于是∠APB>600,而∠APD=∠BPC>∠BCP=90°-15°=75°,所以∠APB+∠APD+∠BPC+∠CPD>60°+75°+75°+150°=360°,与一周角等于360°矛盾,所以AB>PA不可能,同理AB 课堂教学中,教师要帮助学生多方位观察,积极思考,鼓励独立探索和敢于创新的精神,对于学生的新观点和精神给予积极的肯定和鼓励,保持教师对学生的期待感,顺应学生的成功心理,克服怯懦,大胆地发表自己的观点,培养学生敢于创新的自信心,从而最大程度地激发学生蕴含着的无限创造力。 思维定势是指人们在长期的学习过程中所形成的一种习惯性思维方法,它对新知识的学习具有积极的一面也有消极的一面,消极的一面可使学生用已形成的固定思路和习惯考虑问题,用固定了的方法解决问题,造成解题思路受阻、解题过程繁杂。因此在平常的教学过程中,应注意培养学生的创新思维能力,帮助学生摆脱思维定势的消极影响。 例3:求证不论a取什么实数,关于x的方程x2- (a2+a)x+a- 2=0 必有2个不相等的实根。 按常规解法,先计算判别式△,然后根据△的符号再得出结论。 △=(a2+a)2-4(a- 2)=a4+2a3+a2-4a+8 发现它是一个关于a的四次多项式。由于学生思路受“判别式定势”的影响,当求出△时,一时难以判定它的符号,从而解题陷入困境。 倘若我们改变一下思维方法,构造二次函数f(x) =x2- (a2+a)x+a- 2 ,要证明原命题成立,只需证明这个二次函数图象与x轴有2个不同的交点,由于它的开口向上,因此只要找到一个x的值使得y<0,那么问题就解决了。 不难发现,当x=1时f(1) = 12- (a2+a)+a- 2 = -a2-1<0 图象与x轴必须有2个不同的交点,故原命题成立。 在教学过程中,教师应注意消除思维定势的消极影响,引导学生灵活运用知识,挖掘习题的隐含条件,通过变换思考角度, 培养学生思维的深刻性。 数学学科有着严谨的体系和完整的系统,知识间前后照应,密切相联。因此,教师在教学中要遵循系统性原则,掌握好教学内容体系,通过对学生进行系统的知识传授,培养学生思维的深刻性。 例4:已知O是平行四边形ABCD内的任意一点。求证:SΔAOB+SΔDOC=SΔAOD+SΔBOC 以下是这一题型的归类: 一题多解,是从不同角度进行探究得到不同的解题思路,它有利于拓宽学生的解题思路,提高学生的分析问题和解决问题的能力;一题多变,是对于课本的例、习题,或保持已知条件不变,探索是否能得出更深刻的结论,或在原题的基础上适当改变条件、结论,探索是否能得出更一般性的结论。在对变式题的求解的教学中,面对由多种变式变换得来的新题,学生必须分析一些情境的特点,找出已知和未知的联系,或联想,或类比,或推广,重新组织已知的规则,形成新的高级规则,尝试解决新的问题,通过多解变形,有利于培养学生思维的灵活性[2]。 例5:已知a≥0,b≥0,且a+b=1,求a2+b2的最大值和最小值。 解法一:(函数思想) 由a+b=1得b=1-a,则 因为a≥0,根据二次函数的图象与性质可得 当a=1或a=0时,a2+b2的最大值为1。 解法二:(运用基本不等式) 因为a≥0,b≥0,a+b=1, a2+b2=(a+b)2-2ab=1-2ab 解法三:(对称换元思想) 因为,a≥0,b≥0,且a+b=1,可设 解法四:(数形结合思想) 在平面直角坐标系xoy中,设a2+b2=r2(r>0), 问题转化为当r满足什么条件时,⊙O与线段AB有公共点 因为a≥0,b≥0,且a+b=1, 所以 当⊙O过A、B时,a2+b2取最大值1 解法五:(解析几何思想) 设A(1,0)、B(0,1)线段AB上的动点C(a,b) 因为a≥0,b≥0,且a+b=1, 所以 当点C与线段AB的端点重合时,a2+b2取最大值1 下面是对本题的变式和推广: 变式1:已知a、b为非负数,M=a4+b4,a+b=1,求M的最值。 变式2:已知a、b≥0且a+b=1,能求a8+b8的取值范围吗?a6+b6呢?a7+b7的范围能求吗? 对课本例、习题的巧妙变式,及对课本例、习题的一题多解和一题多变训练,可以培养学生多角度、多层次地去思考问题和解决问题,培养学生的思维能力,提高解题能力,同时也能有效的防止题海战术。 综上所述,教师应注重挖掘例、习题内涵,对课本典型例、习题的进行变形处理,帮助学生构建知识网络,加强对学生进行思维训练,促进其良好思维品质的形成。 [1] 颜望辉.“两型”数课堂教学模式研究与实践[J].当代教育理论与实践,2014(11):12-14. [2] 李为.初中数学课堂问题设计例谈[J].中学数学教学参考,2014(8)19-21. (责任校对 晏小敏) 20141203 林永晖(1964-),男,福建永春人,中学一级,主要从事教育管理研究。 10.13582/j.cnki.1674-5884.2015.05.008 G625.5 A 1674-5884(2015)05-0025-043 克服思维定势,培养学生思维的深刻性
4 重视总结提高,培养学生思维的系统性

5 通过多解变形,培养学生思维的灵活性