抑制光伏功率对电网影响的电池管理研究
赵向阳,王杏玄
(北京航空航天大学自动化科学与电气工程学院,北京100191)
抑制光伏功率对电网影响的电池管理研究
赵向阳,王杏玄
(北京航空航天大学自动化科学与电气工程学院,北京100191)
光伏功率难以有效预测、调度和控制,通过储能系统直接与光伏并联运行,可平抑光伏功率的随机性,将其并网时对配电网电能质量的影响降到最低。主要研究使光伏发电的并网功率波动最小的电池管理方法,针对随机量的一般波动性与多尺度波动性指标,提出了对光伏功率进行完全补偿时基于定尺度窗口和变尺度窗口的电池充放电策略,通过仿真,将优化效果以及所需储能系统的容量分别进行比较,得出变尺度窗口比定尺度窗口调度电池具有更好的平抑作用。
光伏并网;电池管理;定/变时间尺度
0 引言
光伏发电的波动性、随机性在并网时给配电网的有功平衡和电压调整带来压力,增加了配电网规划和调度的难度。并网的成功与否在很大程度上取决于其输出功率波动性的大小[1]。文献[2]指出光伏功率具有明显的波动性,在短时间内波动量可超过装机容量的50%。为保证光伏安全并网,需要通过调节储能电池对其输出功率加以限制。文献[1]总结出用不同概率密度函数拟合不同尺度下的光伏功率的出力。文献[3,4]提出了完全补偿的概念并针对储能电池容量已知时电池以恒功率、功率差充放电对微电网与配电网联络线功率的平抑效果进行深入探讨,但是没有对完全补偿时需要的电池容量进行详细阐述。文献[5]在考虑预测误差的影响下研究了如何配置分布式光伏储能系统容量。文献[6]采用动态规划法的电池储能系统的削峰填谷作用进行优化,并在不同充放电次数下的效果进行对比。此外,许多外学者在研究平抑功率波动性方面已取得一定成果[7~17],其中文献[16]是用电动汽车换电站多个电池的有序充电来协同优化波动性功率,但是针对衡量光伏功率波动性的表述过于单一。
本文在讨论随机量均值、方差的基础上,提出了定、变尺度窗口的概念,以平抑光伏并网功率的波动为目标,创新性的以一般、多尺度方差为评价指标,并对按定、变尺度窗口调度值完全补偿功率波动所需电池容量和的优化效果进行比较。
1 电池的管理目标
在光伏并网的工程设计中,必须考虑储能系统对并网功率的平抑效果,本文试图通过控制储能系统的充、放电使光伏并网功率的波动性最小,这里用以下两种指标来衡量其波动性。
1.1 一般波动性
(1)峰谷差
文献[12]从曲线的最大值、最小值入手抑制其波动性的2个函数为:
T时间内随机量X最小值最大为:
f=max{min(X)}
(1)
充电时段内总曲线最大值最小为:
f=min{max(X)}
(2)
文献[13]中以减小曲线峰谷差为目标函数:
FL=min[max(X)-min(X)]
(3)
(2)方差

(4)
1.2 多尺度波动性
为了更全面地描述光伏功率的分布特点,应该研究其在不同时间尺度时的波动性。
(1)阶跃变化率
将原序列的相邻或相间隔数据相减后得到的新序列为原序列的阶跃变化,再除以相减数据的间隔即为原序列的阶跃变化率。阶跃变化的绝对值可在一定程度上反映原序列的波动性大小[10,11]。
假设某序列P的采样时间为Ts,期望在时间间隔为Td时衡量该间隔的阶跃变化,定义阶跃变化为:
(5)

(6)
在此基础上,考虑期望时间间隔的影响,可得到阶跃变化率表达式:
(7)
这个期望时间间隔Td不同,其对应的阶跃变化也不同,从而导致了光伏出力波动的多尺度特性。即假如采样时间Ts为1min,分析每10min、30min、60min等时间间隔的平均功率时,期望时间间隔Td则依次为10min、30min、60min;N依次为10、30、60;若对应一天24 h的功率,L依次为144、48、24。
(2)M-界定
基于阶跃变化、阶跃变化率在衡量波动性时由于将波动平均化而导致计算的波动性偏低失真问题,“M界定”法应运而生,即将原序列在所给时间间隔内的最大值、最小值相减作为波动性的量化指标[8~10]。具体为:
M=Mup-Mlow
(8)
式中:Mlow≤x(t)≤Mup,∀t∈[ε,ε+Δ],ε为某一时间间隔的开始时刻。
(3)统计方差
文献[14]将某随机量划分为若干窗口,其中第i个时间窗口内随机量的平均值为:
(9)
则第i个时间窗口的随机量的方差D为:
(10)
式中:sum(D) 为随机量P的统计方差[5];M为时间窗口的时段数;Pt为第t时段的随机量;Pav,i为第i个时间窗口的随机量平均值。选取不同的M值,可得到随机量P的多尺度波动性,即不同尺度的衡量原来数据的波动性。M的合理取值为3~24,M越大对应的方差表示与该调度点越多的相邻点的波动性;越小越能反映局部波动性。特殊地,当窗口尺度M为24时,sum(D)/(L-1)即为一般意义的方差。
2 电池管理策略
假设精细化调度时,采样频率为5 min,则在1 h内的光伏功率数据有12个,调度时间间隔15 min(窗口尺度至少为3个,变尺度时的要求),本文提出的两种调度思路。
2.1 策略1 定尺度调度
电池充放电的各个区间尺度相等,按n个小时的均值作为一个调度值,这里n满足电池充放电次数和调度时间间隔的约束,可取范围n=1/4~24 h;设充放电区间尺度为调度段的M倍,则待求一天的窗口总数为N=floor(24/M)+1,第i个阶段的始、末节点为:
相邻窗口时间搭界的始末节点为:
a(i)=(i-1)×(M-1)+1
(11)
b(i)=i×(M-1)+1
(12)
2.2 策略2 变尺度调度
此时,电池充放电区间尺度不等,但与策略1中区间个数一样,而且每个窗口内的数据要不小于3个,调度值取为不同时间尺度的窗口均值。该思路由统计方差的思想启发,将随机量按波动程度划分窗口。
各个窗口尺度的选取准则:当前调度节点至末尾调度节点,所有尺度下对应调度后标准差最小的尺度为最优时间尺度。设第k个节点对应第i个窗口(其中k≥i-1),即前i-1个窗口对应的尺度已知,则第i个窗口对应的尺度为:
M(i)=min(std(pi))
(13)
其中,pi=[k,k+1…end],end∈{k+1,k+2,…n},pi为从当前节点k向后至末尾节点n所有尺度下的随机量序列;波动最小的序列,即当前尺度M(i)∈{1,2,…24-k}。
第i个窗口的时间节点为:
a(i)=(i-1)×(M(i)-1)+1
(14)
b(i)=i×(M(i)-1)+1
(15)
第i个窗口均值为:
m(i)=f(mean([a(i)…b(i)]))
(16)
调度电池充放电电功率的值为:
pb(i)=m(i)-mean(m)
(17)
图1是按剩余调度段的标准差最小的原则取随机量的变尺度均值。

图1 随机量的变尺度窗口
2.3 电池充放电指令的生成
理想的调度目标是各个时段的窗口内,并网功率为一恒定值,即无波动性;所有相邻时段的窗口并网功率波动性最小。因此电池的充放电指令应该为:当光伏功率变化为上升趋势且大于各窗口均值的均值时,储能系统的作用相当于将光伏功率“拉低”变化较为平稳的区间,因此储能系统多数时间保持处于充电状态,储能系统充电能量变化表现为上升趋势;当光伏功率变化为下降趋势且小于各窗口均值的均值时,储能系统的作用相当于将光伏功率“抬高”到变化较为平稳的区间,因此储能系统多数时间保持处于放电状态,储能系统充电能量变化表现为下降趋势[3]。则当按上述方法完全补偿光伏功率波动时可求出储能电池的最大容量。具体流程如下图2所示。

图2 电池充放电指令的流程图
2.4 相关约束条件
(1)功率平衡约束
在平抑随机量X(本文是原始光伏功率)波动时,Y是经电池充放电调节后的光伏并网功率。设X为采样频率为5 min离散化的功率值,则在t时刻,可得原始光伏功率X与并网功率Y的关系如下式:
Y=X-pb
(18)
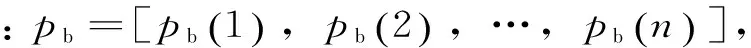
(2)充放电次数约束
当采用全部数据对应的同一个均值时,储能充放电次数太频繁,每5min都要变;即充放电次数约束决定了调度次数,即窗口个数。确定储能系统充放电区间时,根据蓄电池组容量及最大充放电功率约束,结合负荷的峰谷时间段,确定一个或多个连续的充/放电区间,从而有效避免其频繁充放电,延长蓄电池使用寿命;还能避免电池过度充/电,保护电池,此外,在峰谷时段充放电,可有效削峰填谷[4]。
(3)充放电最大功率约束
(19)
t时段的电池充/放电功率|pb(t)|最大不超过PESS,可通过调节总窗口个数改变。
(4)电池容量约束
为满足平抑等效负荷功率波动的需要,储能所需最大容量如下所示:
(20)
(21)
Et为一次充或放电后电池的电量。
(5)日充放电量约束
En=0
(22)
为使电池在每个调度日发挥相同的作用,需保持电池每日的充放电量之和为0,即每天始、末时刻电池的荷电状态(StateofCapacity,SOC)相同。
(6)荷电状态hSOC的定义及其相关约束
hsoc(t)=Qre(t)/Qmax
(23)
hsoc(t+1)=hsoc(t)+pb(t)×Δt
(24)
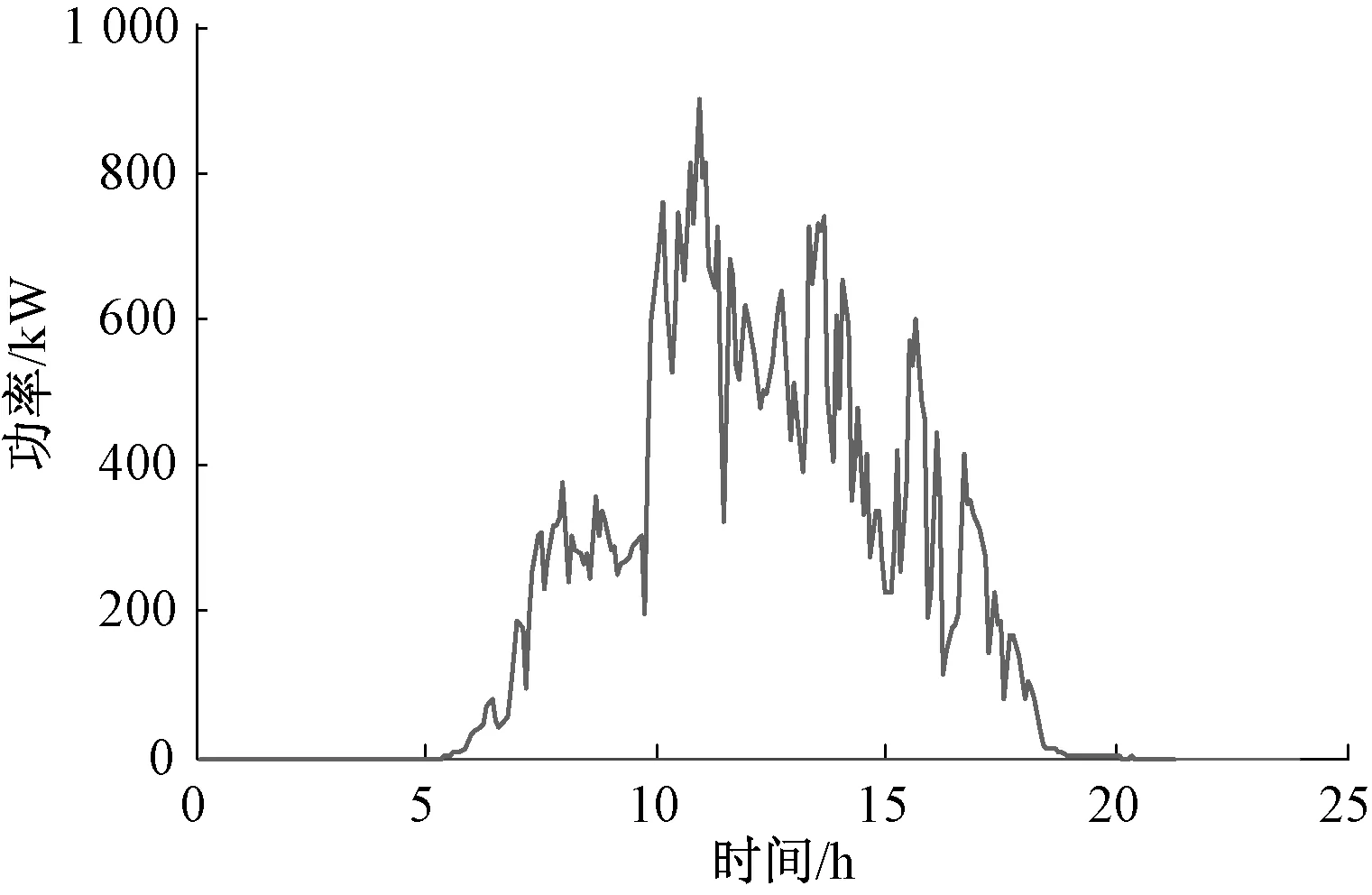
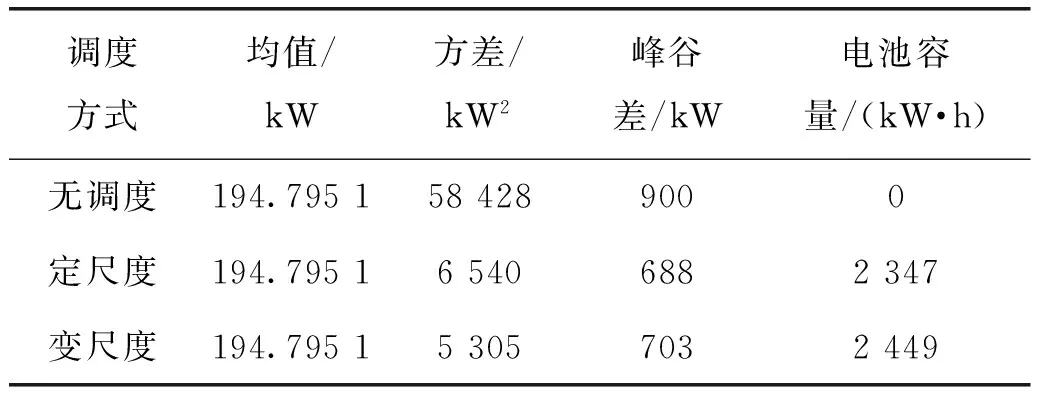
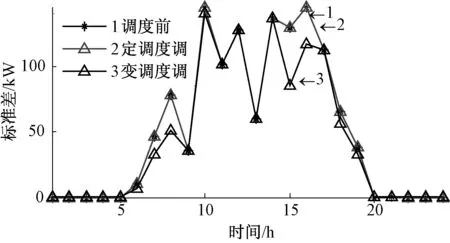
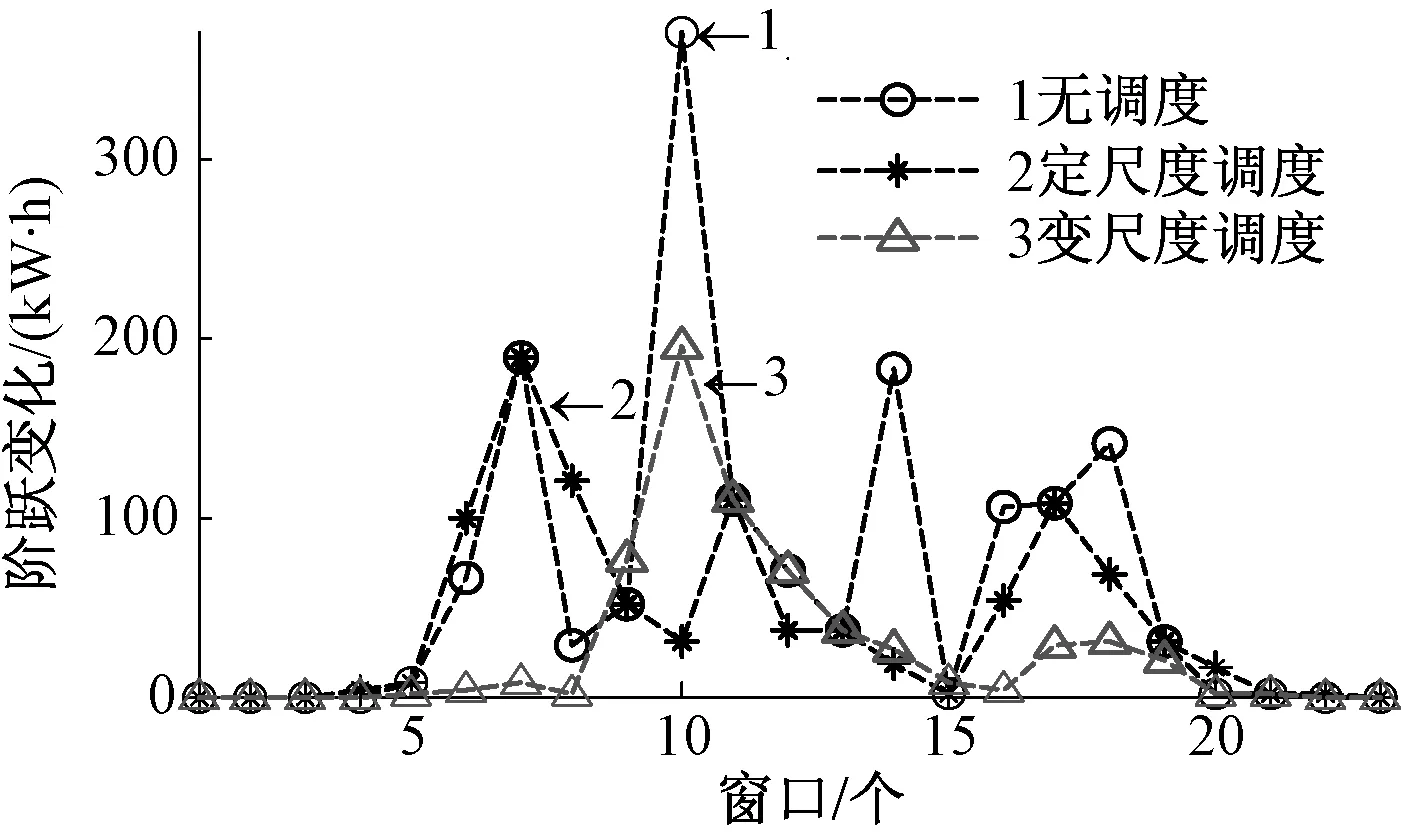
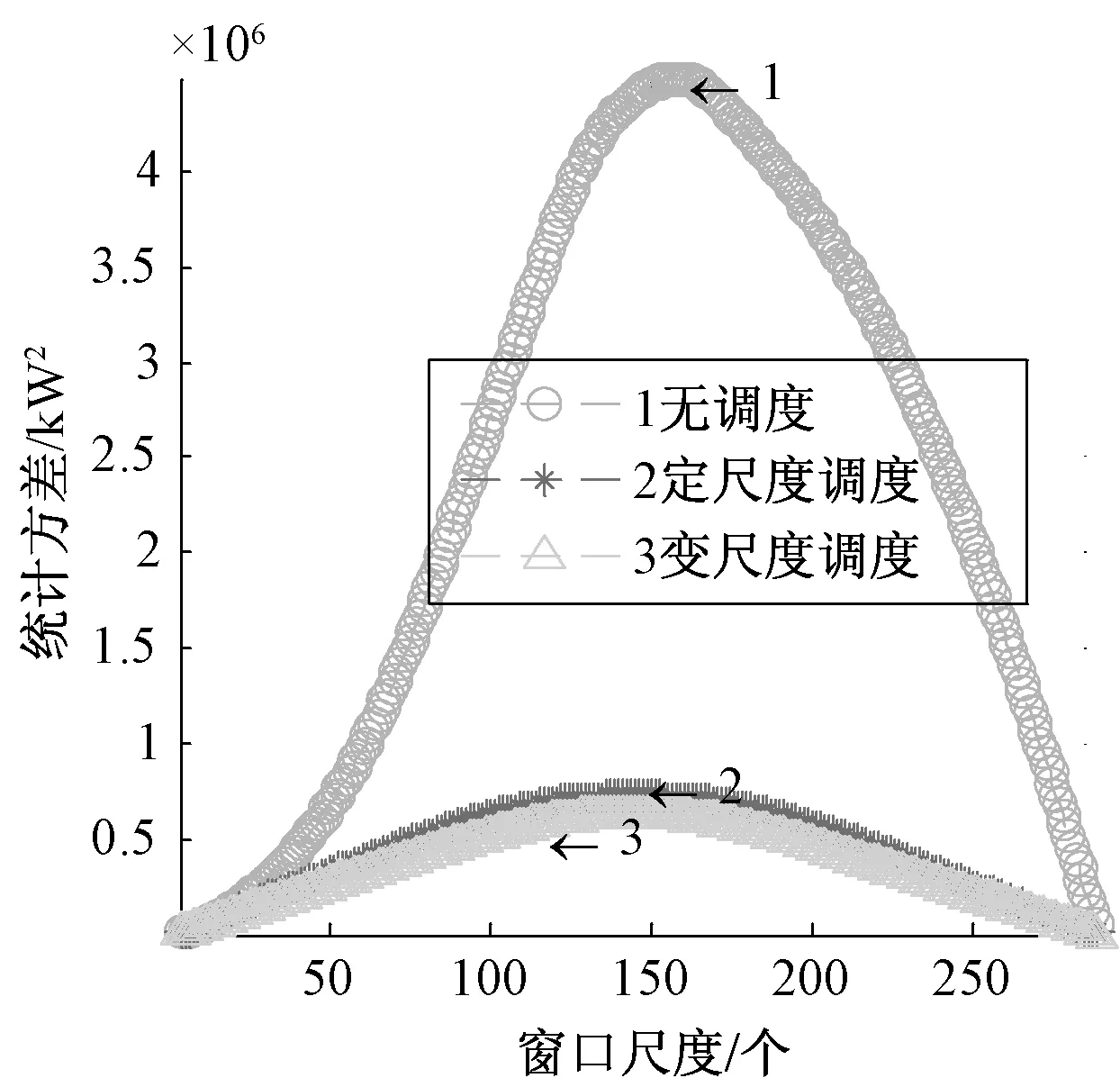
hsoc.max (25) 式(23)中:用hsoc(t)表示电池t时刻的荷电状态,即t时刻的电池剩余容量Qre(t)与其总容量Qmax的百分比;式(24)反映了相邻时段电池荷电状态的关系;式(25)则反映在任何时段都要满足其荷电状态的约束,对蓄电池来说,通常取hsoc.max=1,而考虑到电池过度放电对其寿命的不利影响,hsoc.min常取为 0.2。 3.1 系统介绍 美国Ashland的15kW光伏电站[15]某典型日的光伏出力曲线如图3所示。 图3 光伏功率的波动性 本文设置一天调度次数n=12,即每个定尺度窗口的调度间隔Δt=2 h,变尺度限制最小尺度为 3个采样点的2种调度方案。 3.2 调度效果 定尺度窗口调度电池的效果如图4所示。电池在1~6,18~24时段放电;在6~18时段充电。每2 h保持同一功率进行充/放电,并且充电的功率与光伏功率幅值成正比。 电池电量变化如图5所示。 图4 定尺度12窗口的调度图 图5 定尺度12窗口的电池电量变化图 变尺度窗口调度电池的效果如图6~7所示。 图6 变尺度12窗口的调度图 图7 变尺度12窗口的电池电量变化图 与图4相比,图6对应的电池在充/放电时段间隔不等,但是总窗口数与图4中的一致,均为12个。可见,电池作用是将曲线的均值抬高,但是并没有改变其高频分量,应该用可频繁充放电的超级电容滤波进行平滑。 光伏功率在电池定、变尺度调度后一般波动性的比较如表1所示。 表1 光伏功率的的一般波动性 由表1可见,完全补偿光伏功率波动时,在调度前后其均值保持不变;其一般波动性的不同指标在定、变尺度调度后的都有改善,并且在定、变尺度调度对储能系统容量的要求没有明显区别[18]。 电池调度前,定、变尺度调度后光伏功率的多尺度波动性的比较如下,1 h内均值、标准差如下图8、9所示。 图8 等效负荷1 h均值对比 图9 等效负荷1 h标准差对比 由图可看出,光伏功率在电池定、变尺度调度后1 h均值变化都比调度前平滑很多;1 h 内波动性变尺度比定尺度调度后效果要好。 电池调度前,定、变尺度调度后光伏功率的1 h阶跃变化率、M界定的1 h阶跃变化率分别如图10、11所示。 图10 1 h阶跃变化率 图11 M界定的阶跃变化率 定尺度调度并不能改变M界定的阶跃变化率,即在图11中无调度和定尺度调度的M界定的阶跃变化率的曲线重合,因为在同一小时内减去相同的值,其极差不变。并且图11的M界定的极差阶跃变化率要比图10对应的1 h阶跃变化率要大。 电池调度前,定、变尺度调度后光伏功率的统计方差如图12、13所示。 图12 调度前、后统计方差对比 图13 定、变尺度统计方差对比 由图12可见,无论定、变尺度调度都在很大程度上改变了等效负荷的多尺度波动性,并且在图13中比较,变尺度比定尺度的改善效果更为明显。 本文从衡量随机量的波动性出发,对一般波动性、多尺度波动性进行阐述,在此基础上,提出了定、变时间尺度窗口调度电池平抑光伏功率波动的方法。由于变窗口尺度调度法适度的考虑了数据的相关性,针对光伏功率波动性大的部分缩小调度尺度,波动性小的部分增大调度尺度,变尺度在考虑局部多尺度波动性的同时又照顾了整体的一般波动性,而定窗口尺度调度法是在一个方案里按同一个尺度调度,这样处理数据时显得呆板。最后用一个算例,验证了所提方法的优越性,变尺度调度电池充放电在避免电池频繁充放电的同时更能减弱光伏功率在并网时给配电网带来的冲击的问题。 [1]吴振威,蒋小平,马会萌,等.多时间尺度的光伏出力波动特性研究[J].现代电力,2014,31(1):58-61. [2]王磊.光伏发电系统输出功率短期预测技术研究[D].合肥:合肥工业大学,2012. [3]陈益哲.微网中分布式储能系统的建模与控制研究[D].武汉:华中科技大学,2011. [4]陈益哲,张步涵,王江虹,等.基于短期负荷预测的微网储能系统主动控制策略[J].电网技术,2011,35(8):35-40. [5]林少伯,韩民晓,赵国鹏,等.基于随机预测误差的分布式光伏配网储能系统容量配置方法[J].中国电机工程学报,2013,33(4):25-33. [6]鲍冠南,陆超,袁志昌,等.基于动态规划的电池储能系统削峰填谷实时优化[J].电力系统自动化,2012,36(12):11-16. [7]丁华杰,宋永华,胡泽春,等.基于风电场功率特性的日前风电预测误差概率分布研究[J].中国电机工程学报,2013,33(34):136-144. [8]杨树德,同向前. 风电功率波动特性描述方法比较研究[C]. 分布式发电、智能微电网与电能质量——第三届全国电能质量学术会议暨电能质量行业发展论坛论文集,2013. [9]李剑楠,乔颖,鲁宗相,等.大规模风电多尺度出力波动性的统计建模研究[J].电力系统保护与控制,2012,(19):7-13. [10]林卫星,文劲宇,艾小猛,等.风电功率波动特性的概率分布研究[J].中国电机工程学报,2012,32(1):38-46. [11]李军徽.抑制风电对电网影响的储能系统优化配置及控制研究[D].华北电力大学(北京),2012. [12]李秋硕,肖湘宁,郭静,等.电动汽车有序充电方法研究[J].电网技术,2012,36(12):32-38. [13]韩海英,和敬涵,王小君,等.基于改进粒子群算法的电动车参与负荷平抑策略[J].电网技术,2011,35(10):165-169. [14]张学清.风电预测、协同调调度及电网电压安全评估研究[D].济南:山东大学,2013. [15]张佳伟.光伏并网发电系统短期发电功率预测研究[D].南京:南京信息工程大学,2013. [16]杨爱民,张晨曦,文福栓,等.微网环境下的电动汽车换电站运营策略[J].华北电力大学学报:自然科学版,2013,40(4):19-26. [17]朱铭,黄伟,郭佳欢,等.微网并网时的经济运行研究[J].电网技术,2010,(34):38-42. Research on Battery Management to Reduce the Effect of Photovoltaic Power on Grid Zhao Xiangyang, Wang Xingxuan (School of Automation Science and Electrical Engineering, Beihang University, Beijing 100191, China) It is difficult to forecast, schedule and control photovoltaic power. However, energy storage system with the parallel operation of photovoltaic power device can be used to stabilize randomness of photovoltaic power on grid and minimize the impact on grid quality. This paper studies the battery management method to minimum photovoltaic power fluctuation when connected to the main grid. According to random quantity general and multi-scale volatility index, the battery charging and discharging control strategies based on the fixed window size and varied window size were proposed. By simulation, the optimization effect and the storage system capacity were compared. The results indicate that the variable window size has better stabilization than fixed window size. photovoltaic grid-connected; battery management; fixed/varied temporal scales 2015-07-06。 赵向阳(1967-),男,副教授,研究方向为微电网光伏发电及调度、电气检测及其信息技术。通信作者:王杏玄,E-mail:1064836024@qq.com。 TM743 A 10.3969/j.issn.1672-0792.2015.09.0083 算例







4 结论

