随机扰动时碰摩转子的非线性振动特性研究

李 展, 李 红, 石志刚, 何 青

(1. 华北电力大学 能源动力与机械工程学院，北京102206; 2. 中国能源建设集团 鞍山铁塔有限公司，辽宁鞍山114042)

随机扰动时碰摩转子的非线性振动特性研究

李 展1, 李 红1, 石志刚2, 何 青1

(1. 华北电力大学 能源动力与机械工程学院，北京102206; 2. 中国能源建设集团 鞍山铁塔有限公司，辽宁鞍山114042)

为了研究随机扰动对碰摩转子系统振动特性的影响，建立了随机扰动下的碰摩转子的动力学模型，利用四阶龙格—库塔法对该模型进行求解，得到了系统的非线性振动特性。结果表明随机扰动对碰摩转子的运动特征有显著的影响，这种影响与随机扰动的强度有关。当随机扰动强度系数不超过某一常数时,扰动只影响倍周期分岔点处或者周期运动与拟周期或混沌运动结合点处的周期运动形式，而对原周期运动的影响较小。当随机扰动强度系数大于某一常数时，随机扰动不仅使原周期运动变为拟周期或混沌运动，而且也使原混沌运动的系统行为特征变得更为复杂，振动幅值显著增大。所以在实际的转子系统运行中应尽量减少或避免随机扰动的发生，以使系统运行更加稳定。

碰摩转子；随机扰动；周期运动；拟周期运动；混沌运动

0 引言

任何物体每时每刻都会受到随机扰动的影响，转子系统也不例外。尤其是运行在复杂环境下的大型汽轮发电机组、远洋航行中受到波浪扰动的大型军舰的动力机组等最为明显。因此，对转子系统进行随机扰动的动力学特性分析讨论具有更为重要的意义。

目前国内外都对转子碰摩的非线性特征进行了一些研究。Goldman[2]等在考虑分段刚度、粘性阻尼等因素的影响下，通过数值积分求解表明转子系统具有丰富的超谐响应、次谐响应和混沌响应等运动形式。候兰兰[3]以Jeffcott转子为研究对象分析了碰摩系统随转速和阻尼变化的振动特征。刘小亮[4]分析了蒸汽压力变化对汽轮机运行的影响。杨志安[5]分析了转子系统随转子半径、气密磁隙等参数变化的特性。康锦萍[6]分析了气隙计算长度、定子漏抗对汽轮发电机组的影响。袁惠群[7]考虑机匣的弹性和陀螺力矩等因素的影响，建立了碰摩转子的动力学模型，并用稳定性理论得到研究了各参数对系统运动的影响。罗跃刚[8]考虑转子材料的物理非线性特征，发现系统具有倍周期、阵发性和倍周期倒分岔等丰富的运动特性。

从目前的研究来看，针对故障转子在随机激励下的研究较少。所以本文以局部碰摩转子为研究对象，建立考虑油膜力的碰摩转子的动力学模型，研究系统在不同随机扰动强度系数下随转速和圆盘阻尼等参数变化的非线性振动特征。

1 碰摩模型

本文以径向局部碰摩为研究对象，建立碰摩模型[9]，如图1(a)、(b)所示。假设转子两端由两个完全相同的滑动轴承支承，两端轴承的位移也完全相同，转轴为无质量弹性轴。O为静止时转子的质心位置，OO1为转子径向位移，圆盘中心坐标(x,y)，轴承中心坐标为(x1,y1)，用轴承间隙δ0无量纲化有

(1)

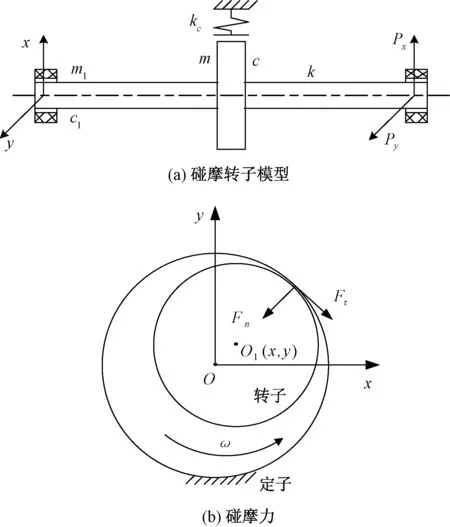
图1 碰摩转子模型

假定定子径向变形为线弹性变形，转子与定子间的摩擦符合库仑定律，即摩擦力Fτ与作用于接触面上的正压力Fn成正比

Fτ=fFn

(2)

式中：f为摩擦系数。

面积作为生活中常见的六种物理量之一，面积的教学为今后角度、体积、容积的学习奠定了度量基础。在“面积”的再教学中，通过“把握面积概念，渗透度量意识”“感知面积单位，发展度量意识”“理解面积公式，感悟度量本质”，学生初步把握了度量的数学结构，逐步增强度量观念，有效地落实了本单元的教学。

(3)

式中：ks为定子径向刚度，N/m。

根据式(3)，当r>δ时，碰摩力Fn在x,y方向上的分力分别为

(4)

无量纲形式为

(5)

关于油膜力，本文采用具有较高精度和收敛性好的非线性Ca-pone模型[10]，其无量纲形式为

(6)

其中，

(7)

(8)

(9)

(10)

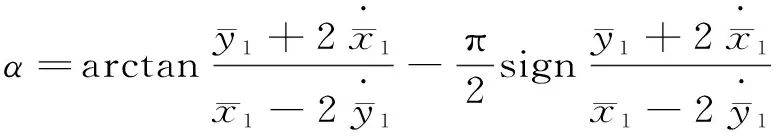
(11)

所以，非线性油膜力为

(12)

其中，s为Sommerfeld修正系数

(13)

式中：μ为润滑油黏度，Pa·s；W为转子和圆盘重量的一半，kg；L为轴承的长度，mm；R为轴承半径，mm；ω为转子转速，rad/s。

2 运动方程

由于实际运行中的汽轮机叶片会受到气流力的扰动，即假设随机扰动信号加在圆盘的x方向上，则系统在随机扰动下的无量纲运动微分方程为

(14)

其中

(15)

3 系统参数与仿真方法

本文仿真的碰摩转子系统参数如表1所示[12]。

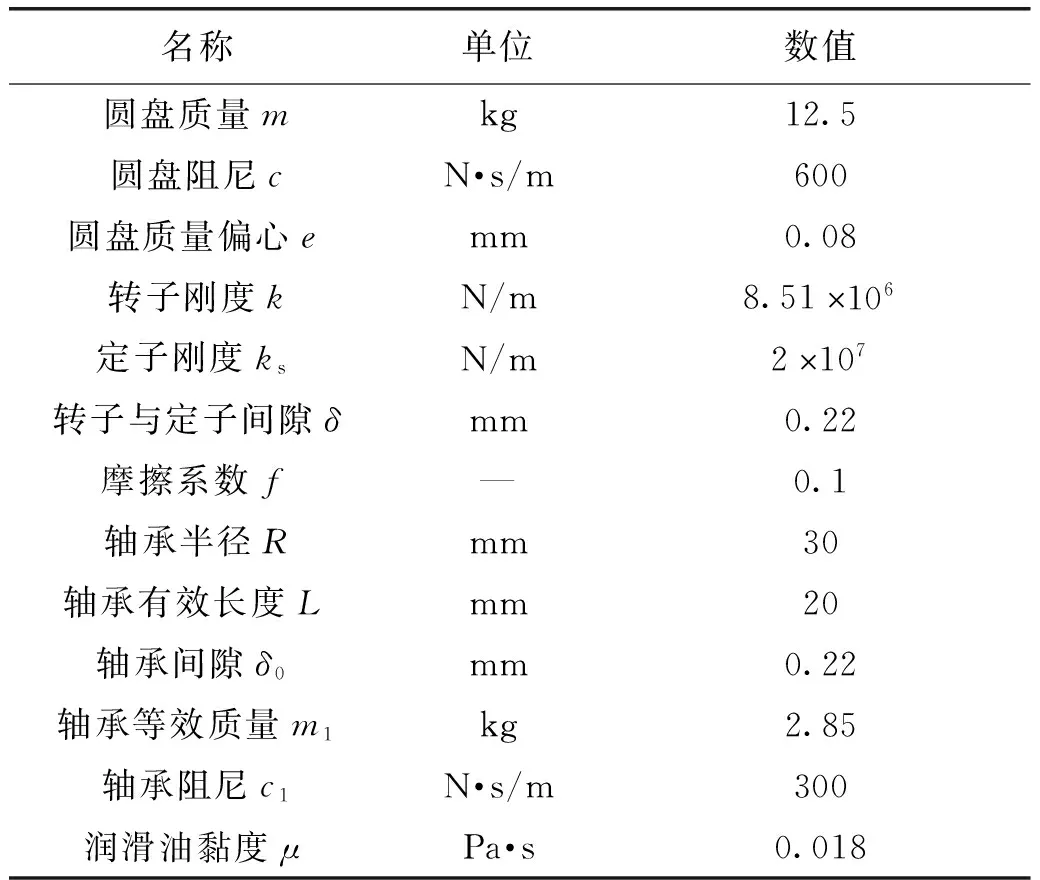
表1 碰摩转子系统参数

方程(14)为随机激励非线性周期时变系统，其中的随机扰动项即方程(15)使用Monte-Carlo随机模拟的方法进行模拟，最后对方程(14)使用四阶龙格—库塔法进行求解。

本文选取转速和圆盘阻尼为参数来模拟不同随机扰动强度系数下的转子系统的非线性特征响应。此外，在本文的研究中，按式(15)构造不同的随机扰动样本，最终得到的碰摩转子的非线性特征响应基本相同，所以也从侧面可以印证用式(15)得到的白噪声过程是满足各态历经条件。

4 仿真结果与分析

4.1 转速对碰摩转子非线性特性的影响

图2(a)为圆盘随转速变化时的分岔图，响应特征如表2所示。从图2(a)和表2可以看出，当系统无扰动时圆盘在不同的转速下表现出复杂的运动状态。当转速较低时碰摩力较小，油膜力在转子运动中起主导作用，系统表现为稳定的P-1周期运动。随着转速的升高，在油膜力和碰摩力共同作用下，圆盘在560 rad/s时突然出现失稳现象进入拟周期状态，之后由于碰摩力的增大系统重新经倒分岔现象进入P-2周期运动状态，然后又经倍分岔现象进入P-4周期运动，最后进入混沌运动。图2(b)为加入较小随机扰动强度系数即当σ=0.000 55的情况下的圆盘随转速的响应。从图2(b)中可以看出，小的扰动只是让分岔曲线变得更粗了一点，而周期解与拟周期解的交汇点，倍分岔点以及周期解与混沌解的交点的位置基本无变化，此时的转子运动规律与无扰动时的响应与表2所示基本相同。当加入的随机扰动强度系数增大到σ=0.002时，如图2(c)所示，转子转速为390rad/s时就由P-1周期运动进入拟周期运动且一直持续到混沌运动状态，而转子在无扰动或小扰动时由P-2周期到P-4周期再到混沌运动的级联现象也模糊不清了。

图2 系统响应随转速的分岔图

图3～5为系统在典型转速ω=1 150rad/s下的响应。从图3(a)、(b)、(c)中可以看出，系统首先由无扰动下的周期轴心轨迹变为微小扰动下的一簇环形轨迹，最后变成了较大扰动下的混乱轨迹。从图4(a)相图中的封闭曲线和图5(a)中有4个点可以看出，此时系统做P-4周期运动。从图4(b)可以看出，如果加入的随机扰动强度系数较小，此时的相图也变成了一簇环形轨迹，再参照图5(b)中庞加莱截面图中形成了闭合的圈形，说明此时系统开始做拟周期运动，但系统整体上还是稳定的。从图4(c)中可以看出，再增大随机扰动强度系数后，此时的相图变得混乱，图5(c)中庞加莱截面包含有分散堆积的散点，形成了两个混沌岛，所以，可以判定此时系统做混沌运动。

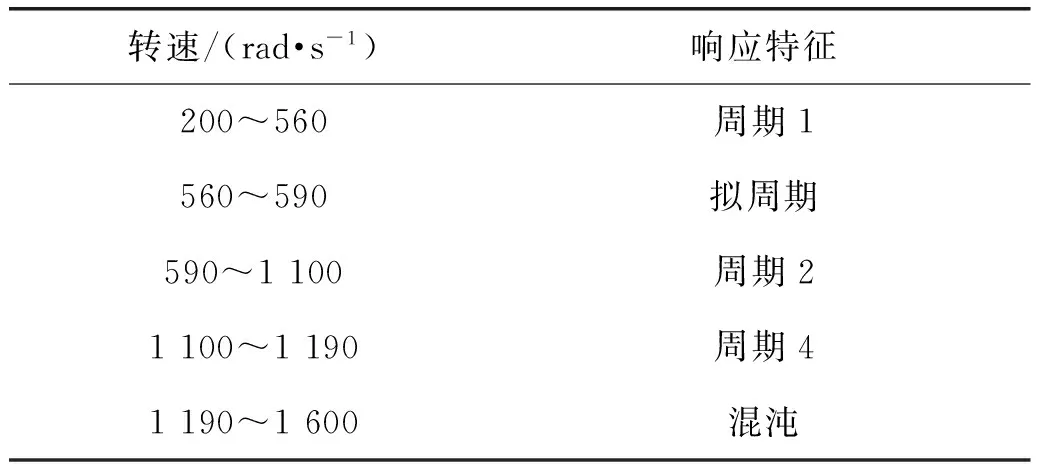
表2 系统响应随转速的变化(σ=0)

图3 轨迹图

图4 相图

图5 庞加莱截面图

4.2 阻尼对碰摩转子非线性特性的影响

图6(a)为无扰动时系统在转速为700 rad/s且其他基本参数不变的情况下转子振动随圆盘阻尼变化的分岔图，响应特征如表3所示。从图6(a)和表3中可以看出，系统随着圆盘阻尼从小到大要经历周期、拟周期、混沌等复杂状态。当圆盘阻尼较小时，油膜力占主导作用，所以做周期运动。随着圆盘阻尼的增加，当圆盘阻尼为1 000 Ns/m时系统出现阵发性跳跃进入拟周期运动，然后经过倒分岔进入周期运动，随后又由阵发性跳跃到混沌运动。当圆盘阻尼大于1 800 Ns/m时，系统做稳定的周期运动。由此可见，圆盘阻尼越大，系统的运动越稳定，但是同时增加系统的能量消耗。当向系统中加入微小的扰动后，如图6(b)所示，此时系统的运动规律基本与无扰动的情况相同，只是周期曲线变得更粗了一点。但是，当向系统中加入较大扰动时，如图6(c)所示，系统的周期曲线不但变得更粗，而且使得原系统的倒分岔现象变得模糊不清，即周期运动变成了拟周期或混沌运动。

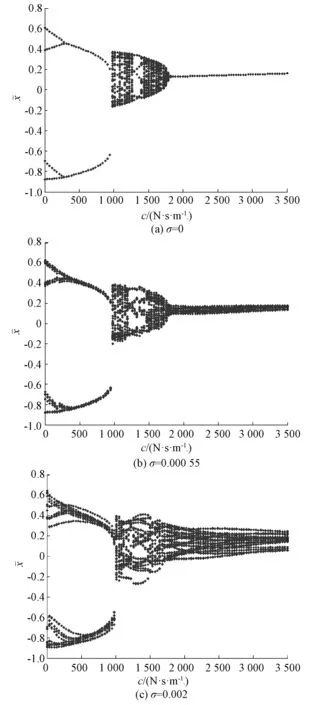
图6 系统随轮盘阻尼的分岔图

圆盘阻尼/(N·s·m-1)响应特征0～300周期4300～1000周期21000～1240拟周期1240～1400周期51400～1800混沌1800～3500周期1

从图7到图9为系统在转速为700 rad/s，轮盘阻尼为1 350 Ns/m时的典型响应。从图7(a)、(b)、(c)中可以看出，小的随机扰动强度系数可以使原系统的有规律的闭曲线周期解变为一组非闭曲线的扰动下的周期解，加大随机扰动强度系数后轴心轨迹线变的非常混乱，即此时系统做混沌运动。从图8(a)相图中包含5个闭曲线，图9(a)中有5个点，可以判断系统此时做周期P-5运动。从图9(b)庞加莱截面图中形成了一条闭曲线，可以判定现在系统做拟周期运动，这反映在轨迹图中就是轨线变成了一簇闭合的曲线环。当σ=0.002时，从轴心轨迹图和相图中可以看出此时的轨迹在区域中来回折叠形成了一组混乱的图形，反映到庞加莱图中如图9(c)包含有大量的散点，形成了云状的图形，即此时系统做混沌运动。

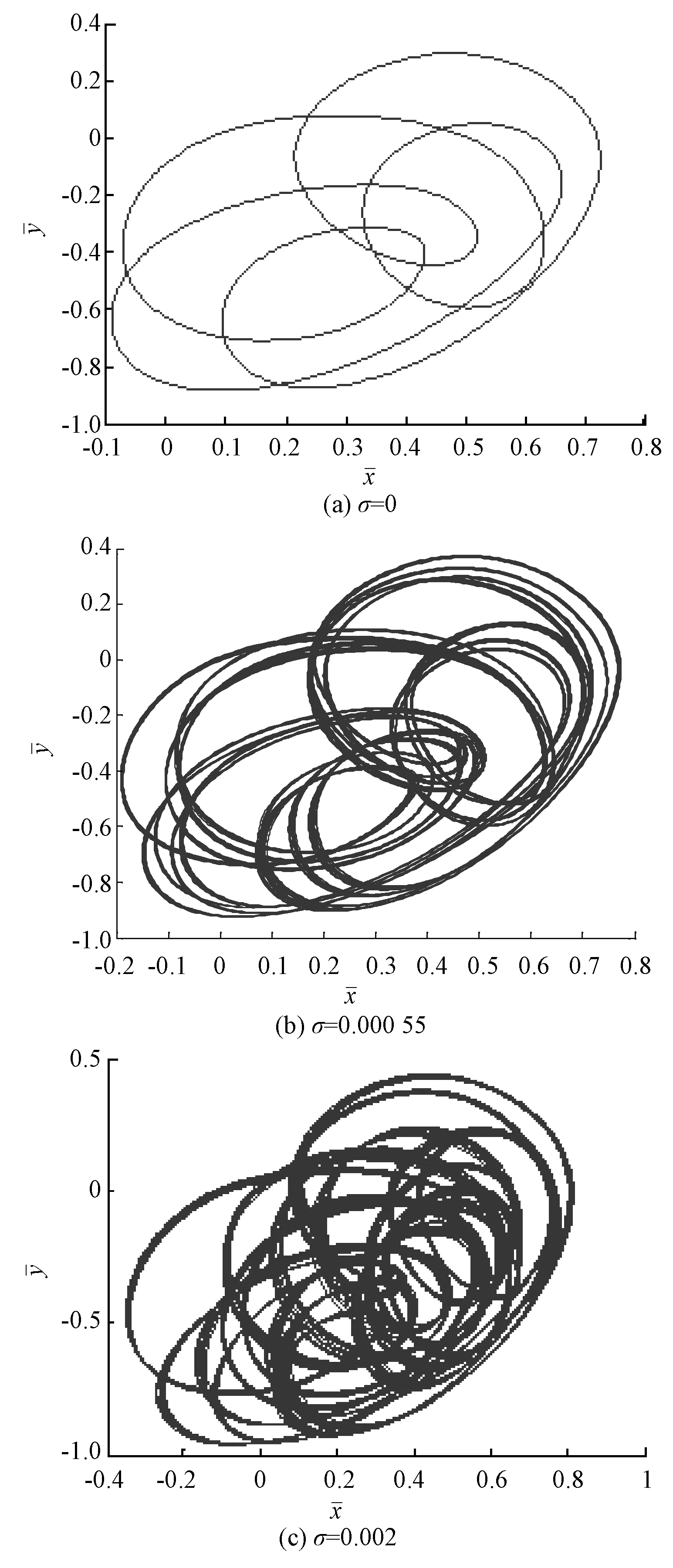
图7 轨迹图

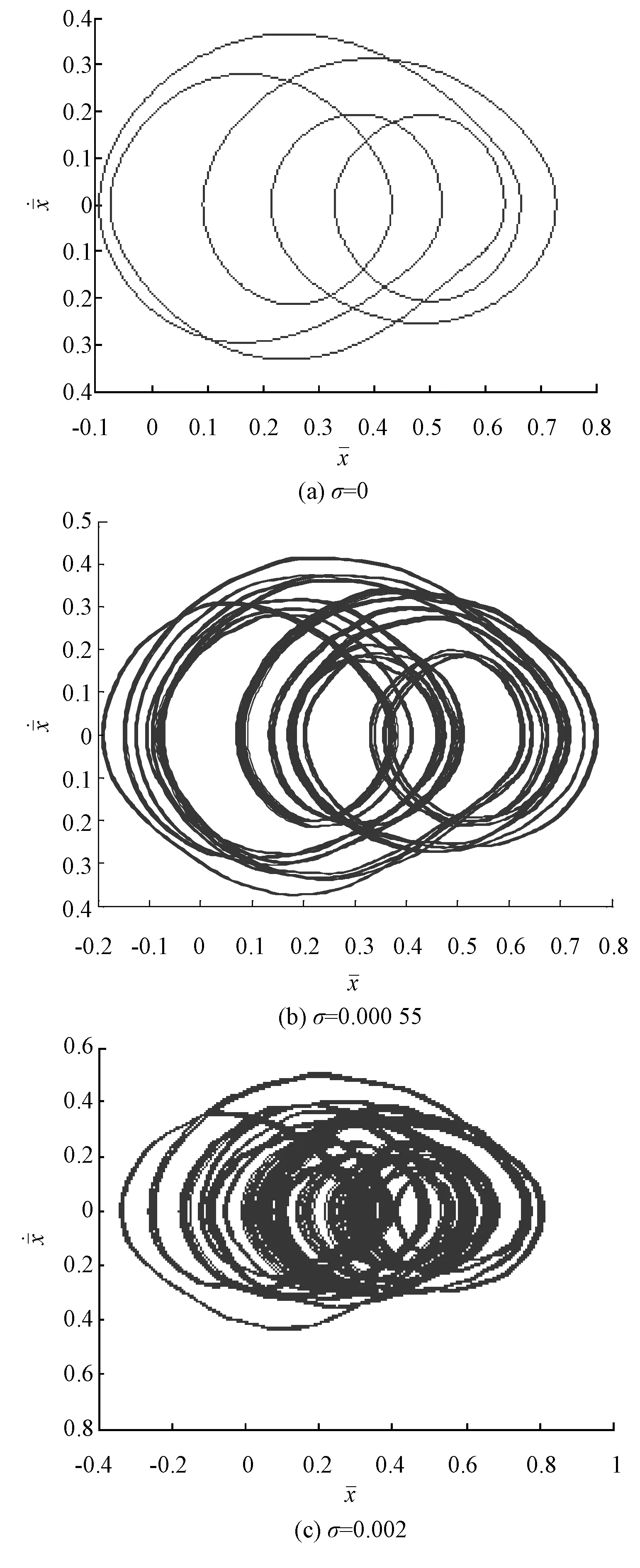
图8 相图

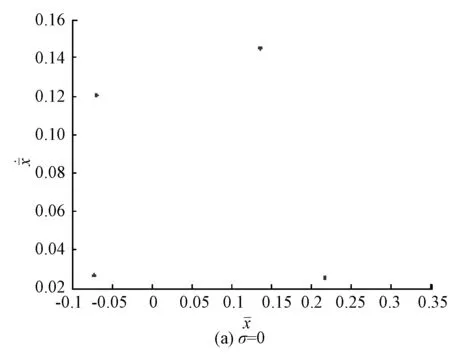
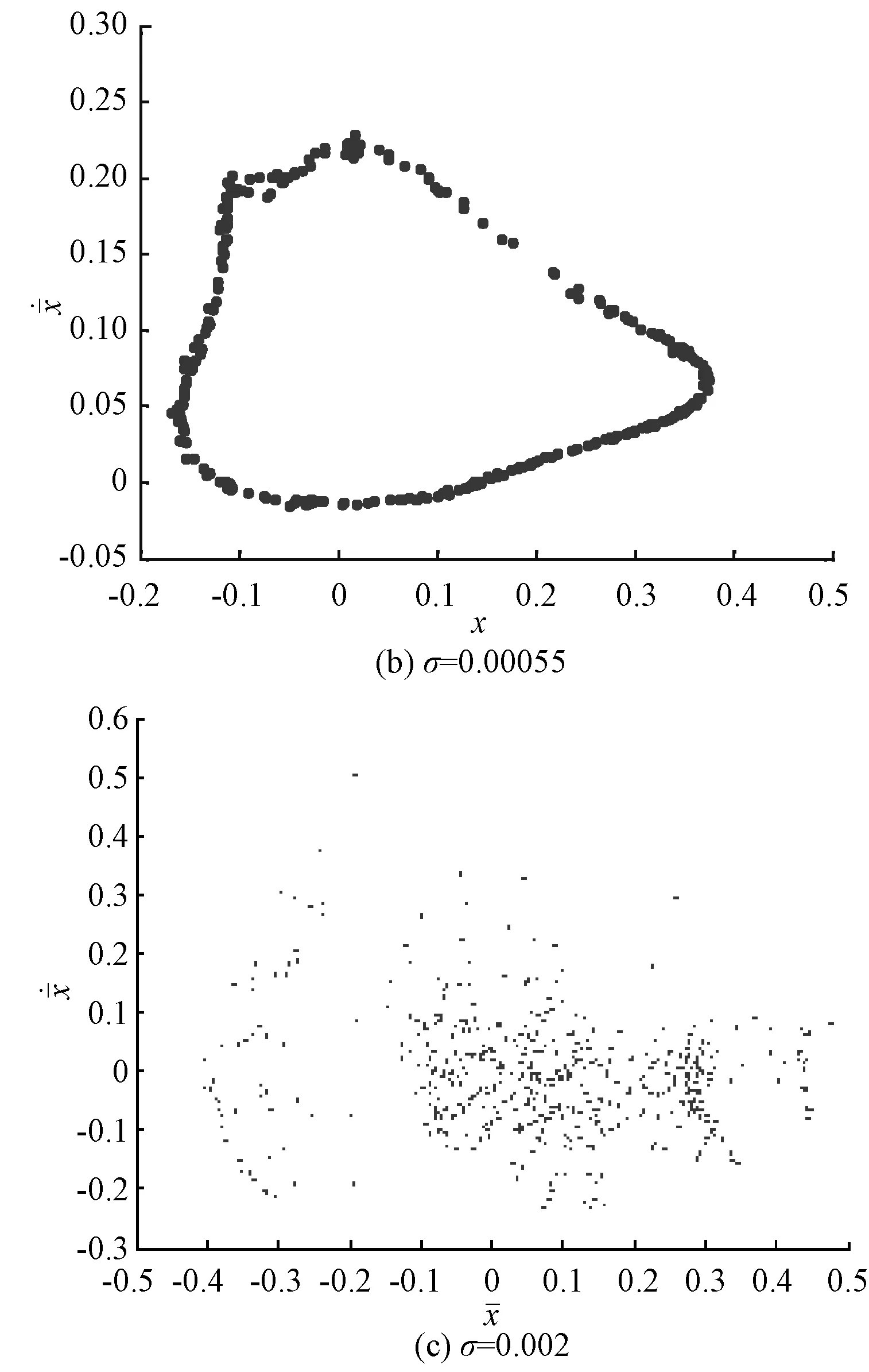
图9 庞加莱截面图

5 结论

本文建立了碰摩转子系统的动力学模型，分析了随机扰动强度系数对系统的影响，得到以下结论：

(1)在本文中当随机扰动强度系数小于0.000 55时，随机扰动主要影响系统的倍周期分叉点以及周期运动和拟周期或混沌运动的结合点处的运动，一般使系统的周期运动数增加，而不能使系统进入拟周期或混沌运动的状态。此时随机扰动对系统周期运动影响很小，可以忽略。

(2) 在本文中当随机扰动强度系数大于或等于0.000 55时，随机扰动对整个系统的运动造成较大的影响,可以使周期运动变成拟周期或混沌运动，且使原有的拟周期或混沌运动的位移显著增大。

[1]张楠，刘占生，姜兴渭. 高速转子轴承系统碰摩故障仿真研究[J]. 振动与冲击，2010，29(9)：77-81.

[2]GoldmanP，MuszynskaA.Dynamiceffectsinmechanicalstructureswithgapsandimpacting：orderandchaos[J].JournalofVibration&Acoustics，1994，116(4)：541-547.

[3]候兰兰，向玲. 转子系统碰摩的非线性动力学分析[J]. 华北电力大学学报:自然科学版，2014，41(3)：64-69.

[4]刘小亮，张雪敏，秦博宇，等. 蒸汽参数变化对汽轮机系统稳定性影响的机理分析[J]. 电力科学与工程，2015，31(4)：52-57.

[5]杨志安，孟佳佳. 电动机轴承转子系统弱非线性主共振分析[J]. 机械强度，2015，37(1)：13-17.

[6]康锦萍，徐英辉. 汽轮发电机稳态有限元模型中计算参数对仿真结果的影响[J]. 电力科学与工程，2015，31(5)：29-33.

[7]袁惠群，王正浩，闻邦椿. 弹性机匣双盘碰摩转子系统的稳定性[J]. 振动与冲击，2010，29(8)：52-54.

[8]罗跃纲，鲍文博，金志浩，等. 非线性刚度不平衡转子动力学行为研究[J]. 振动与冲击，2002，21(3)：84-86.

[9]许琦，姚红良，刘子良，等. 双碰摩故障转子系统碰摩位置定量诊断方法[J]. 振动与冲击，2014，33(12)：24-27.

[10]闻邦椿，武新华，丁千，等. 故障旋转机械非线性动力学的理论与试验[M]. 北京：科学出版社，2004. 30-56.

[11]冷小磊，孟光，张韬，等. 考虑随机扰动时裂纹转子系统的分岔与混沌特性[J]. 振动工程学报，2006，19(2)：212-218.

[12]陶海亮，潘波，高庆，等. 具有弹性静子的碰摩转子轴承系统非线性动力特性研究[J]. 振动与冲击，2013，32(15)：197-202.

NonlinearCharacteristicsResponseofRub-impactRotorbyRandomDisturbance

Li Zhan1, Li Hong1,Shi Zhigang2,He Qing1

(1.School of Energy Power and Mechanical Engineering, North China Electric Power University, Beijing 102206, China;2. Anshan Iron Tower Factory, China Energy Engineering Corporation Ltd., Anshan 114042, China)

This paper establishes the system dynamics model with white noise as random disturbance in order to study the nonlinear vibration characteristics of rub-impact rotor system. And the Fourth-Order Runge-Kutta integral method is employed to obtain the numerical solution. It shows that random disturbance signal has a significant impact on the movement characteristics of the rub-impact rotor, and this effect has a close relationship with the strength of disturbance signal. Generally speaking, random disturbance affects the period-doubling bifurcation point or the combining site of system movement between periodic motion and quasi periodic or chaotic motions only when the strength of disturbance signal is smaller than a constant. But when the strength is bigger than a constant, it not only makes the original periodic motion turn into a quasi periodic or chaotic motion, it also renders the original chaotic motions of the system more complex. So it needs to reduce or avoid the random disturbance in order to make the system steadier.

rub-impact rotor; random disturbance; periodic motion; quasi-periodic; chaos

2015-06-29。

中央高校基本科研业务费专项资金资助(2014MS17)。

李展(1990-),男,硕士研究生,研究方向为汽轮发电机组振动故障的非线性问题. E-mail：huadianlizhan@163.com。

TK 261

A

10.3969/j.issn.1672-0792.2015.09.010